随机脉冲协议下的多智能体系统的包容控制
朱胜楠,吴小太
(安徽工程大学 数理与金融学院,安徽 芜湖 241000)
近年来,多智能体系统在无人机编队飞行、移动机器人的协同控制、电网的协同控制等方面都有着广泛的应用,这也使得多智能体系统的一致性问题引起了越来越多专家学者的研究兴趣[1-2]。多智能体协作控制中一个基本且普遍存在的问题就是一致性控制,其目的是设计分布式控制算法,使一组有或者没有领导者的智能体在某些特定状态达成一致[3-6]。当多智能体系统中有多个领导者时,研究的一致性问题也被称为包容控制,其中跟随者能够在一定状态下收敛到由多个领导者组成的凸包上[7]。到目前为止,对于非周期采样、嘈杂的混合环境和延时的多智能体系统的包容控制,在参考文献[8-10]中已经有了大量的结果,当然这些结果都是基于连续控制的研究。
脉冲控制是一种有效的间断控制策略,已成为现代控制论的重要控制方法之一,与连续控制相比,脉冲控制是一种更方便、鲁棒性更强、更有效的间断控制策略[11],只需要在特定时刻改变系统的状态即可。特别是对于大规模分布式控制,智能体之间的信息交互会产生一定程度的消耗,连续时间控制会造成通信资源的极大浪费。因此,在过去几十年中,对各种复杂网络考虑了脉冲控制的一致性问题[12-13]。Wang等[14]通过脉冲混合控制研究了具有或不具有时滞的Duffing型振荡器的完全同步问题。Yang等[15]研究了延迟脉冲系统的稳定性。Tang等[16]通过脉冲控制研究了具有时滞的准同步问题,进一步促进了脉冲效应,即脉冲控制在结果中起了积极和消极的作用。工程技术、环境生态、社会经济等领域中出现的实际系统一般都带有外界的干扰。
拒绝服务(Denial of Service,DoS)攻击的目的是阻止收发器之间的通信,通常包括周期性DoS攻击、随机DoS攻击和任意DoS攻击[17-18]。DoS攻击者通过干扰通信通道来实施攻击行为,通常会导致控制性能下降,甚至不稳定。在文献[19]中通过对DoS频率和持续时间施加适当的限制,输入状态稳定性被考虑用于动力系统。通过利用这些假设,尽管存在DoS攻击,仍对稳定性或者一致性进行了广泛的研究[17,20-21]。到目前为止,对于多智能系统问题,特别是同时考虑随机脉冲的情况下,脉冲控制问题还没有得到充分的研究。这可能是因为在这种情况下,很难设计合适的时间脉冲控制协议来描述随机波动,另一方面,如果脉冲受到随机DoS攻击,则很难采用文献[19]中常用的假设来描述DoS攻击下有脉冲。因此,如何描述脉冲的DoS可能是一个值得研究的问题。
基于上述讨论,研究考虑了多智能体系统的随机脉冲包控性问题。首先,对随机脉冲协议下的多智能体系统包容控制问题进行了研究,其中脉冲控制协议由时间触发决定。其次,研究提出了一种时变概率来描述对每个脉冲输入进行DoS攻击的可能性,并研究了在随机拒绝服务攻击下多智能体系统的脉冲包容控制问题。
1 相关定义与引理
本文考虑一个由M个领导者和N个追随者组成的多智能体系统。追随者的动力学行为描述为
(1)
式中,ui(t)∈n和xi(t)∈n分别表示第i个跟随者的输入和状态;A是具有兼容维度的常数矩阵。领导者的动态如式(2)所示。
(2)
式中,xκ(t)∈n代表第κ个领导者的状态。
假设N+M个智能体之间的信息交换用图GN+M=(V,ε,A)表示,其中,V={1,…,N,N+1,…,N+M}表示满足非空性和有限的节点集,ε⊆V×V是边集,A=(aij)∈(N+M)×(N+M)表示邻接矩阵。在矩阵A中,aij是边(j,i)的权重,当且仅当(j,i)∈ε时,aij>0,否则,aij=0。(i,j)∈ε表示的边意味着代理j可以从代理i接收信息,其中代理j被称为代理i的邻居。代理i的邻居集由Ni={j∈V|(j,i)∈ε}表示。设D=diag{d1,d2,…,dN}为度矩阵,其中,是接普拉斯矩阵。
接下来考虑系统式(1)、式(2)的包容控制问题,给出一些必要的假设、引理和定义如下。

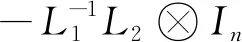
定义1[24]对于∀i∈F={1,…,N},多智能体系统式(1)、式(2)的包容控制目标是通过提议的协议实现的,如果
dis(xi(t),Co(xκ(t),κ∈L))→0,ast→∞,
(3)
式中,Co(xκ(t),κ∈L)表示由xκ(t)组成的凸包。
为了实现多智能体系统式(1)、式(2)的一致性,脉冲控制协议定义如式(4)所示。
(4)
式中,γk是一个随机变量,用于描述脉冲强度的随机性;{τk}k∈是一个增量脉冲序列,limk→∞τk=+∞;δ(t)是狄拉克函数。
注1:在脉冲控制过程中引入序列随机变量{γk}k∈+来刻画脉冲控制过程中的随机波动。在文献[25-27]中对带有随机脉冲的动力系统进行了一些重要研究。与这些结果相比,研究的创新之处体现在以下两个方面:①研究假设随机脉冲由时间触发机制决定,并在这种机制下解决了多智能体系统包容控制问题;②当随机脉冲受到随机DoS攻击时,给出了保证多智能体系统达到包容控制目标的充分条件。
令
可以检查一下式(5):
(5)


(6)
则在期望意义上实现包容控制目标,即所有追随者的状态收敛到领导者的状态所形成的凸包。
2 时间触发随机脉冲
在本节中,假设控制协议(式(4))中的脉冲是时间触发的,并且多智能体系统式(1)、式(2)可以重写为
(7)
式中,∀κ∈L,i∈F,k∈。假设随机变量γk可以服从不同的分布。
假设2 设{γk}k∈为随机变量序列,且γk∈Λ为任意k∈N,其中,Λ={ξ1,…,ξr}是一组独立的随机变量,ξν=φν,1≤ν≤r。
在假设2中,r中不同类型的脉冲强度用r个随机变量表示。下面,提出一个定义描述每个脉冲强度的脉冲效应。
定义2[26]设Nν(t,s)为时间间隔(s,t]内第ν种脉冲强度的出现次数。如果存在正常量τaν与N0ν,则对于1≤ν≤r,
那么τaν和N0ν分别称为第ν种脉冲强度的平均脉冲间隔和弹性数。可以得到
(8)
在下文中,提供了一个定理,证明可以使用脉冲协议(式(4))实现包容控制目标。
定理1 假设1、假设2成立。如果存在正定矩阵P和常数φ,则
(IN⊗A)TP+P(IN⊗A)≤φIN⊗In,
(9)
(10)

证明构造一个Lyapunov函数如式(11)所示:
V(η(t))=ηT(t)Pη(t)。
(11)
可以由式(5)和式(7)得到
(12)
对于任何t∈[τk,τk+1)和k∈,意味着对于t∈[τk,τk+1),
(13)
根据式(13)、式(9)可知,
(14)
这意味着
V(η(t))≤V(η(τk))eφ(t-τk),
(15)

V(η(τk))=
(16)
式中,Θk=(IN-γkL1)⊗In。设Fk=σ{γ1,γ2,…,γk}是由γ1,γ2,…,γk生成的σ代数。可以证实
(17)
由式(16)与式(17)可知,
V(η(τk))≤Ξk
(18)

V(η(t))≤
因此,对于任何t≥t0,
V(η(t))≤
(19)
从式(10)可以得到
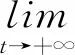
(20)
因此可以得到
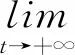
(21)
由上可知,脉冲控制协议(式(4))解决了多智能体系统期望意义上的包容控制问题(式(7))。
注2:在定理1中,引入时间触发的脉冲包容控制,以保证所有跟随者的状态能够收敛到由领导者的状态在期望意义上形成的凸包,其中脉冲强度是随机的。随机脉冲强度用于描述脉冲控制过程中的随机波动,它还可用于描述受到随机拒绝服务攻击的脉冲。
3 结论
本文引入随机脉冲来描述脉冲控制过程中的随机波动。在随机脉冲协议下,假设脉冲为时间触发的,研究了多智能体系统的包容控制。此外,如果脉冲受到随机DoS攻击,提出一个时变概率来描述每次DoS攻击的可能性,并获得了实现在DoS攻击下多智能体系统的包容控制的充分条件。

