时钟模型辅助的惯性/卫星紧组合导航算法研究

董 亮，许东欢，臧中原，孙昭行，罗雪溶

(上海航天控制技术研究所，上海 201109)

0 引言

组合导航系统就是把具有不同特点的导航系统组合在一起，取长补短，以提高导航系统的精度。由于卫星导航系统和惯性导航系统各有其优缺点，全球卫星导航系统(Global Navigation Satellite System，GNSS)能够提供实时的位置、速度信息，并且精度不随时间变化。捷联惯性导航系统(Strapdown Inertial Navigation System，SINS)是一种完全自主的导航系统，具有不受外界电磁干扰、数据更新率高等特点。由于SINS和GNSS具有很强的互补性，因此，对二者进行组合可以获得更好的性能。

当接收机在城市或者峡谷等复杂环境中，卫星信号容易受到遮挡或者干扰，从而导致卫星信号丢失。当可见卫星数少于4颗时，GNSS接收机不能正常定位，此时惯性/卫星松组合导航系统只能工作于纯捷联惯性导航解算模式，而基于伪距/伪距率的紧组合导航系统可以正常工作，但由于观测量不足，系统仍然会发散。本文针对上述问题，提出了时钟模型辅助的惯性/卫星紧组合导航算法，该算法通过正常情况下的钟差、钟漂估计值建立钟差和钟漂的数学模型，在可见卫星少于4颗时，用钟差、钟漂模型计算得到的钟差和钟漂作为系统的真实值，并省去状态变量中的钟差和钟漂项，增加了系统的可观测性。最后，通过采集跑车试验数据进行离线数据仿真试验，比较了传统方法和本文方法在可见卫星少于4颗情况下的定位、测速精度。试验结果表明，本文提出的时钟模型辅助的惯性/卫星紧组合导航算法在可见卫星不足的情况下取得了较好的效果。

1 时钟误差模型

单模卫星接收机定位测速最少需要4颗可见卫星，通过4颗可见卫星的位置、速度以及伪距、伪距率信息就可以解算出载体的三维位置、速度以及接收机的钟差和钟漂等信息。以载体位置计算为例，具体公式如下

(1)

式中，(=1,2,3,4)为第颗卫星到载体的伪距；(,,)(=1,2,3,4)为第颗卫星的位置；(,,)为载体的位置；为光速；δ为卫星接收机时钟误差。

为了在可见卫星少于4颗时计算载体的位置，需减少式(1)中的未知量个数。通常，同一个接收机的钟差在一定时间内是一个随机常值。因此，本文将正常紧组合状态下估计出的接收机钟差的平均值作为接收机的实际钟差，即将正常紧组合状态下的钟差估计值进行累加，当可见卫星少于4颗时，计算估计出的钟差平均值并作为接收机的实际钟差，这样式(1)就可简化为

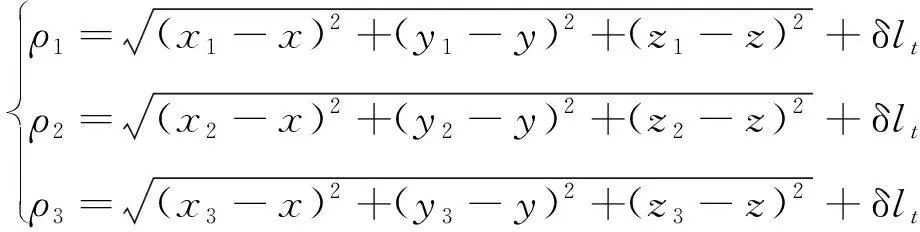
(2)

式中，δ为估计出的接收机钟差平均值。

通过式(2)可以实现可见卫星为3颗时的定位解算。

同样，接收机钟漂可以认为是随时间线性变化的值，可以利用正常紧组合情况下估计出的接收机钟漂对接收机的时钟漂移进行拟合。本文通过一阶线性模型=+拟合卫星接收机的钟漂，选取2个时刻的钟漂估计值计算出拟合模型，在可见卫星数为3颗时，用拟合得到的钟漂作为接收机的实际钟漂进行解算。这样就可以在可见卫星数为3颗时解算出载体的速度。

试验中用到的卫星接收机的钟差、钟漂的正常估计值以及模型拟合值如图1和图2所示。模型拟

图1 卫星接收机时钟误差Fig.1 The clock error of satellite receiver

图2 卫星接收机时钟漂移Fig.2 The clock drift of satellite receiver

合曲线前100s为正常组合状态，100s后设置卫星数少于4颗，正常估计值曲线全程可见卫星数不少于4颗。

传统惯性/卫星紧组合导航系统实现稳定的定位测速也至少需要4颗有效卫星的数据，当可见卫星少于4颗时，由于观测量不足，紧组合导航系统可能会发散。本文通过正常紧组合情况下的钟差、钟漂估计值建立钟差和钟漂的数学模型，在可见卫星少于4颗时，用钟差、钟漂模型计算系统的钟差和钟漂作为真实值，并省去常规紧组合状态下状态变量中的钟差和钟漂项，减少了待估计量个数，增加了系统的可观测性。

2 系统状态方程

常规的惯性/卫星紧组合导航系统Kalman滤波状态变量维数为17维，由捷联惯导子系统的15个状态量(3个姿态失准角、3个速度误差、3个位置误差、3个陀螺常值漂移以及3个加表常值偏置)和卫星接收机的2个状态量(钟漂等效距离率误差、钟差等效距离误差)构成。

考虑可见卫星数少于4颗时，通过钟差、钟漂模型计算系统当前时刻的钟差、钟漂值作为真实值，因此，卫星接收机的2个状态量(钟差和钟漂)不作为少星情况下的状态量，则选取的惯性/卫星紧组合导航系统的状态变量为15维，即捷联惯性导航子系统的15个基本状态量。具体状态方程如下

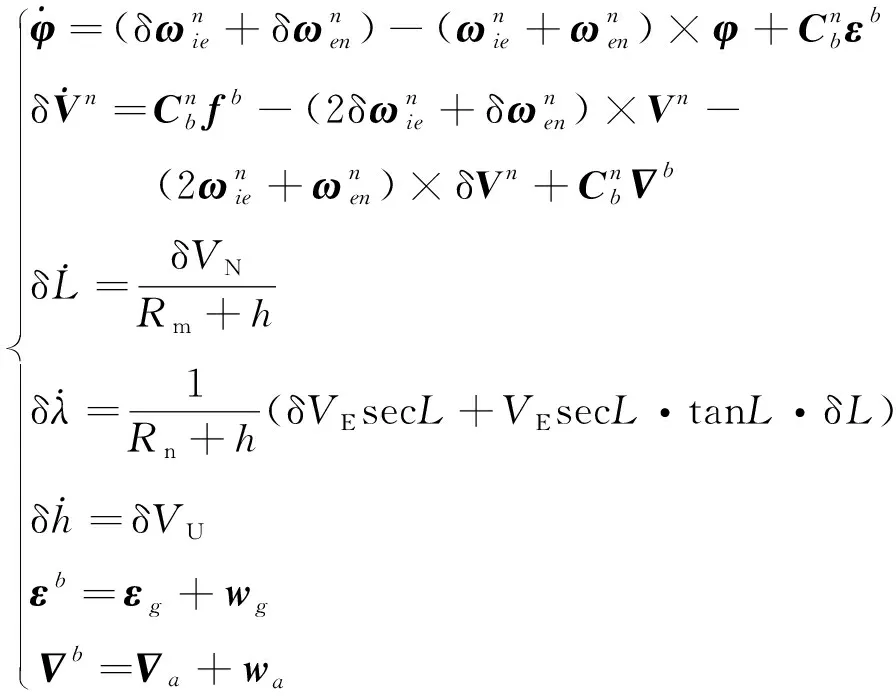
(3)

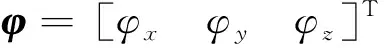
(4)

3 系统观测方程

卫星接收机解算得到的载体与第颗GNSS卫星之间的伪距可以表示为

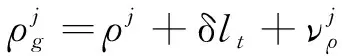
(5)

捷联惯性导航解算得到的载体位置[]与第颗卫星之间的伪距为

(6)

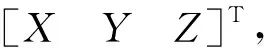
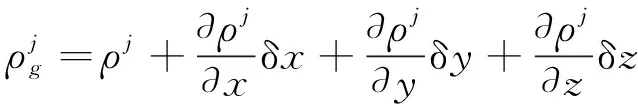
(7)

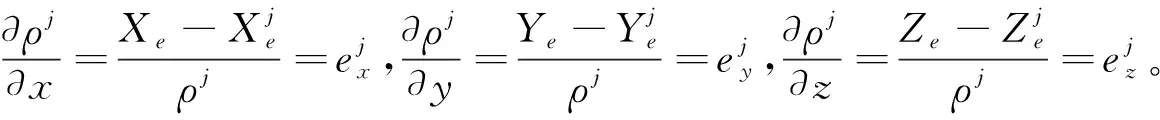
结合式(5)和式(7)，可得惯性/卫星紧组合导航系统的伪距观测方程如下

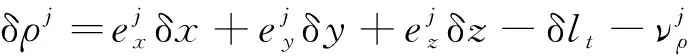
(8)

在可见卫星数少于4颗时，用拟合得到的钟差作为真实钟差对卫星接收机输出的伪距进行补偿，则式(8)可转化为

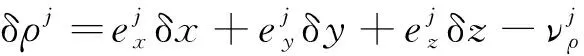
(9)

式(9)即为可见卫星数少于4颗时的卫星/惯性紧组合伪距观测方程。

同理，卫星接收机解算得到的载体与第颗卫星之间的伪距率可以表示为

(10)

根据惯性导航解算得到的载体速度[]，可以计算出与第颗卫星之间的伪距率为

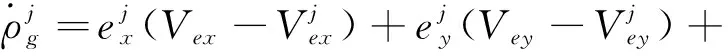
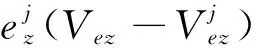
(11)

(12)

其中

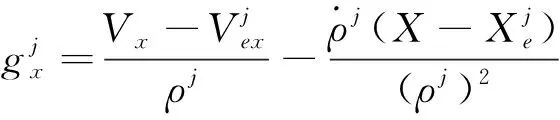
结合式(10)和式(12),可得惯性/卫星紧组合导航系统的伪距率观测方程为

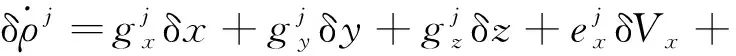
(13)

在可见卫星数少于4颗时，用数学模型拟合得到的钟漂作为真实钟漂对卫星接收机输出的伪距率进行补偿，则式(13)可转化为

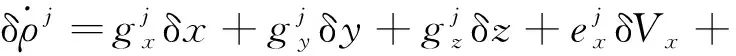
(14)

式(14)即为可见卫星数少于4颗时的惯性/卫星紧组合伪距率观测方程。

结合式(9)和式(14)，可得时钟模型辅助的惯性/卫星紧组合导航算法的观测方程。

4 试验结果与分析

为了验证本文提出的时钟模型辅助的惯性/卫星紧组合导航算法的正确性和有效性，进行了跑车数据离线仿真试验，比较了传统惯性/卫星紧组合导航方法和本文提出的时钟模型辅助的惯性/卫星紧组合导航算法在少星情况下的定位、测速精度。

首先，在进行跑车试验的过程中采集GNSS接收机数据和惯性测量数据，陀螺仪和加速度计的数据5ms存储一次，GNSS接收机数据0.1s存储一次。跑车试验过程中的惯性测量单元(Inertial Measurement Unit，IMU)和GNSS接收机的参数如表1所示，跑车试验实物图如图3所示，跑车试验位置二维轨迹如图4所示。用跑车试验中采集的离线数据进行离线仿真试验，建模时间分别设置为100s、80s、60s、30s、25s，建模完成后将有效卫星数分别设为3颗和2颗。试验结果如图5～图8所示。

表1 惯性测量单元和卫星接收机参数

图3 跑车试验实物图Fig.3 Picture of vehicle experiment

图4 车载试验水平位置Fig.4 Horizontal position of vehicle experiment

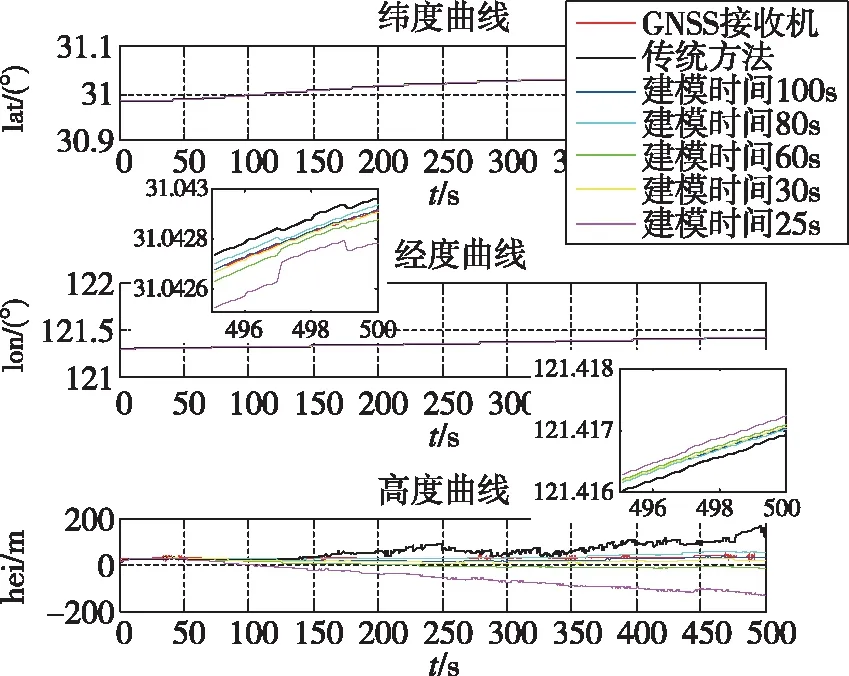
图5 3颗可见卫星下位置曲线Fig.5 Position curve in case of 3 visible satellites

图6 3颗可见卫星下速度曲线Fig.6 Velocity curve in case of 3 visible satellites

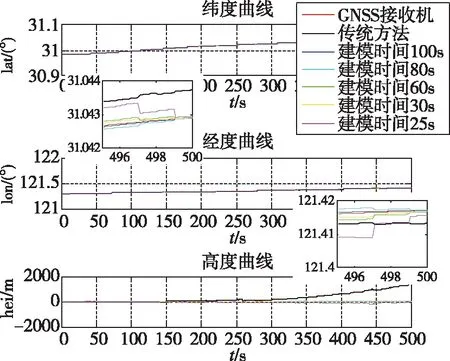
图7 2颗可见卫星下位置曲线Fig.7 Position curve in case of 2 visible satellites

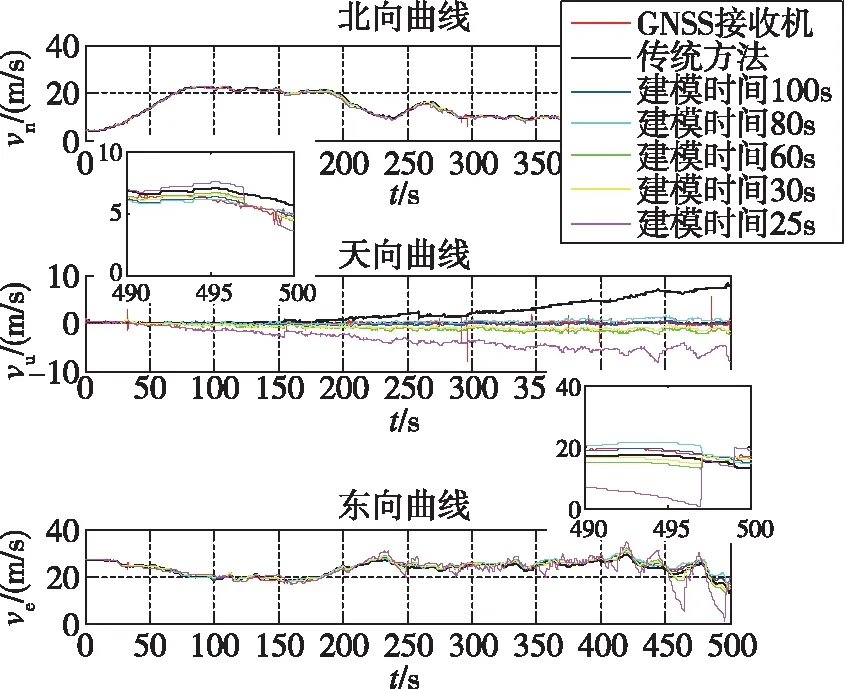
图8 2颗可见卫星下速度曲线Fig.8 Velocity curve in case of 2 visible satellites

通过图5～图8和表2可以看出，在可见卫星少于4颗(3颗和2颗)、建模时间大于25s时，本文方法的定位测速精度明显优于传统方案；在建模时间小于25s时，钟差、钟漂模型的精度明显降低，定位测速误差明显变大。具体结果如表2所示。

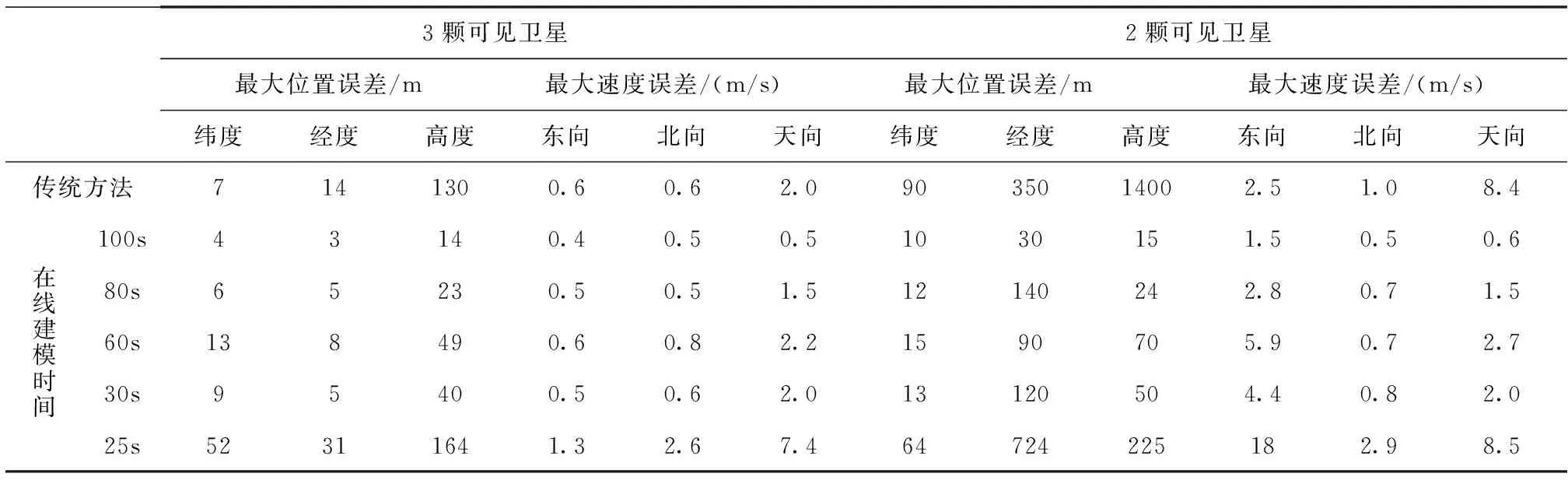
表2 传统方法和本文方法试验结果对比

5 结论

本文针对可见卫星少于4颗时的组合导航方案，提出了一种基于钟差、钟漂模型辅助的惯性/卫星紧组合导航算法，该算法通过正常情况下的钟差、钟漂估计值建立钟差和钟漂的数学模型，在可见卫星少于4颗时，用钟差、钟漂模型计算系统的钟差和钟漂，并作为钟差、钟漂的真实值。通过采集跑车试验数据进行离线仿真试验，比较了传统方法和本文方法在可见卫星少于4颗情况下的定位、测速精度。结果表明，本文设计的基于钟差、钟漂模型辅助的惯性/卫星紧组合导航算法在可见卫星数少于4颗时具有较好的效果，在建模时间大于25s时，定位精度比传统方法提高了2倍以上，定位和测速精度明显高于传统方法。