面向视觉着陆的高精度结构化约束特征点研究

涂 颖，张 海，2

(1. 北京航空航天大学自动化科学与电气工程学院，北京 100083；2.飞行器控制一体化技术重点实验室，北京 100083)

0 引言

无人机传统导航方式有惯性导航系统(Inertial Navigation System，INS)、全球定位系统(Global Po-sitioning System，GPS)和INS/GPS组合导航系统等，近年来视觉导航成为新的研究热点，特别是对于小型低成本无人机，视觉导航有着十分重要的意义。视觉着陆是视觉导航的关键技术之一，且全自主视觉着陆技术对于有人机也有着重要意义。

提高视觉导航着陆抗干扰能力的关键，在于提取出图像中最为稳定的特征点。传统特征点主要有尺度不变特征变换(Scale Invariant Feature Transform，SIFT)、加速鲁棒性特征(Speed Up Robust Featu-res，SURF)、加速分割检测特征(Features from Accelerated Segment Test，FAST)以及定向FAST和旋转BRIEF特征(Oriented FAST and Rotated BRIEF, ORB)等，它们都是从几何约束出发，主要是基于几何不变性和光度不变性等假设，没有利用到环境中存在的结构约束。当场景光照、相机视角等条件发生改变时，特征点也会随之变化。传统特征点提取算法不能保证检测出稳定存在的特征点，会影响视觉着陆的精度与可靠性。

文献[5]提出了一种基于地面红外合作目标和机载红外视觉系统的着陆方案，满足无人机全天候自主着陆要求；文献[6]设计了由多个合作Apriltag标签进行联合定位的算法，以提升无人机定位精度和识别帧率；文献[7]采用了由6个圆心已标识的红色圆组成的地标，并基于仿射变换和支持向量机分类器设计了地标识别方法。这些视觉着陆方案都是针对合作地标的，不能实现真正的自主性。

为了实现基于鲁棒的非合作特征的视觉着陆，本文选取图像中的直线交点作为结构化约束特征点。通过算法设计检测出降落平台中跑道线角点等结构化约束特征点，并对其进行高精度定位，获取抗干扰能力强、定位达到亚像素精度的特征点，为视觉相对定位提供具有高位置精度的图像特征。

1 基于直线交点的结构化约束特征点粗定位

在环境中，线特征往往比点特征更加稳定。提取直线交点作为结构化约束特征点，能够提高特征点的抗干扰性能。当视角变化时，相对于点特征和区域特征，直线交点具有更高的稳定性，对于视觉着陆应用更具有实际意义。

因直线灰度梯度方向具有一致性，可利用这一特性进行给定方向直线段的检测，进而提取线段交点，并结合Shi-Tomasi角点检测算法，实现对结构化约束特征点的粗定位。

1.1 基于梯度一致性的边缘检测

首先，将图像转换为灰度图像，并对图像进行高斯平滑，减少图像整体噪声并保留边缘信息。

图像中像素(,)处的灰度值为(,)，沿、方向的灰度梯度(,)、(,)计算公式如下

(,)=⊗(,)
(,)=⊗(,)

(1)

(2)

其中，⊗表示卷积操作，进而以(,)表示直线边缘的梯度方向

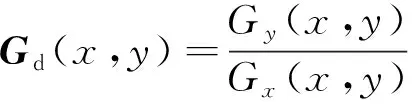
(3)

为提高直线交点的检测效率，应舍弃梯度值较小的像素点，保留具有明确界限的边缘区域。实际应用中，以经验值对梯度方向进行筛选

(,)=

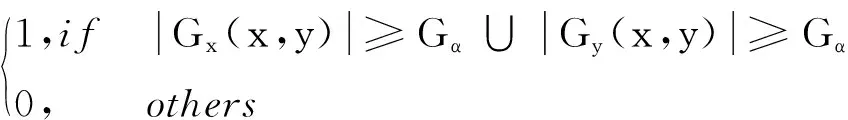
(4)

′(,)=(,)&(,)

(5)

其中，&表示对矩阵进行按位与操作，将掩膜矩阵(,)与梯度矩阵(,)进行按位与操作，舍去梯度值较小的像素点。

为实现直线边缘方向的分类，设计边缘方向分类滤波器，以竖直向下的方向为0°方向，逆时针旋转依次增加22.5°，生成如图1所示的16个主方向的图像梯度分类集合。

图1 图像梯度方向分类示意图Fig.1 Gradient direction classification of visual image

将梯度分类记为()，=1,2,…,16，设置梯度方向的正负阈值分别为和，保证集合具有一定的容错性。

设计直线边缘检测滤波器，模板函数映射如下

()=((-1)*225°,,),
=1,2,…,16

(6)

其中，()为直线边缘检测滤波器，滤波器模板为半径为的圆形，直线边缘宽度设置为。如图2所示，滤波器模板方向与梯度分类方向一致。

图2 直线边缘检测滤波器模板Fig.2 Filter template of line edge detection

将对应相同主方向的图像梯度集合和直线检测滤波器进行卷积，统计这16个主方向的像素点个数

()=()⊗()

(7)

设置阈值，若像素点统计值小于阈值，则认为是曲线或是较短的线段，需将其剔除，实现如下

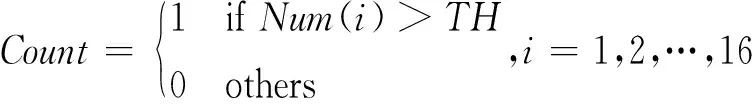
(8)

其中，为边缘一致性检测提取出的特征直线段；阈值取值通常为滤波器模板半径的1.5倍。

对于如图3所示的降落平台，结构化约束特征点集中在白色标识线部分。设置合适阈值，提取出图像中特定方向特征直线段，如图4所示。

图3 降落平台原图Fig.3 Original image of the landing platform

图4主要是为了提取出视觉图像中白色标识线部分的水平短边缘，并通过设置较大的梯度方向正负阈值和，提取尽可能多的长边缘，用于结构化约束特征点的粗定位。

图4 特定方向特征直线段提取结果Fig.4 Extraction results of feature straight segments in particular direction

1.2 结构化约束特征点粗定位

将提取出的特定方向直线段进行组合，获取由直线段交点形成的角点

()=()()

(9)

其中，()由给定方向特征直线段()和()组合而成。

图5所示为结构化约束特征点初步提取效果，由于直线边缘检测滤波器中的直线具有一定宽度，特征点在直线交点区域内不唯一，并且精度不够。

对以初步提取的特征点为中心的小矩形区域，使用Shi-Tomasi角点检测算法提取强角点，实现对结构化约束特征点的粗定位。

(a)结构化约束特征点初步提取效果

(b)细节放大图图5 基于梯度一致性边缘检测算法的结构化约束特征点初步提取效果Fig.5 Preliminary result of structural constrained features based on gradient consistency edge detection algorithm

2 结构化约束特征点的精定位

基于梯度一致性的边缘检测算法对模糊边缘也具有一定的提取效果，能有效确定结构化约束特征点的所在区域，但粗定位的部分特征点位置存在偏移，无法直接用于相对定位解算；而直线段检测算法(Line Segment Detector, LSD)包含图像中直线段端点信息，能够计算得到直线段斜率，有利于设计亚像素角点定位精度改进算法。

设计改进LSD算法，在以粗定位结构化约束特征点为中心的小区域内，提取特征直线段，并求解线段交点。设计亚像素角点定位精度改进算法，结合Shi-Tomasi角点检测算法，将结构化约束特征点精度提高到亚像素级，从而实现结构化约束特征点的精定位。

2.1 改进LSD算法设计

LSD算法主要用于提取图像中的局部直线段轮廓，能够检测出图像中绝大部分的线段结构，并且算法速度快、效果好。利用LSD算法，提取以粗定位结构化约束特征点为中心的矩形区域内的特征直线段，效果如图6所示。

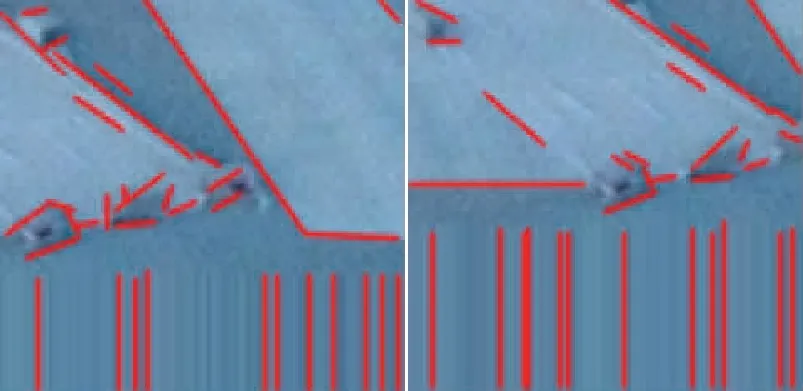
图6 LSD算法效果Fig.6 Results of LSD algorithm

LSD算法在区域增长过程中会对使用过的像素进行标记，导致图像中的每一个像素至多只能属于一条直线段；外部环境存在遮挡等情况时，直线段也会被割裂成多段。因此，需要对LSD算法进行改进。

通过直线斜率筛选，得到候选线段集合

(10)

其中，为衡量线段斜率接近程度的筛选阈值。

通过端点距离筛选，得到候选线段集合

=

(11)

其中，为衡量线段端点接近程度的筛选阈值。

通过中点斜率筛选，得到最终候选线段集合

=

(12)

其中，为衡量线段中点斜率接近程度的筛选阈值。

然后在更为连续的线段集合中寻找到相交的线段，提取出结构化约束特征点。将可能相交的两条线段构成线段集合

={,∈|>,<}

(13)

其中，为线段和的斜率差；为线段和最近的端点距离。式(13)表示线段相交判定准则，即两条线段的最近端点的距离小于给定值，且斜率之差大于给定值。

为便于匹配，对线段进行直线参数化描述，结构化特征约束点即是参数化直线的交点，从而得到结构化约束特征点集合

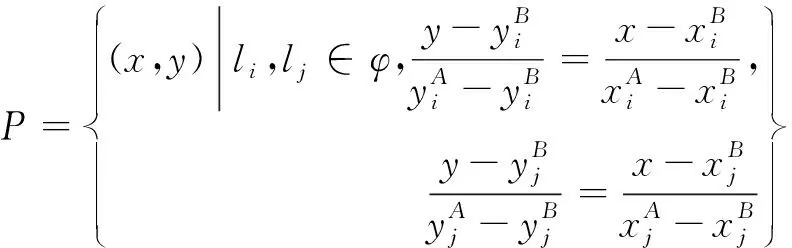
(14)

图7所示为LSD算法改进前后特征直线段提取情况，改进后的算法有利于剔除过短的线段，实现了被割裂线段的有效接续，保留较为鲁棒的线段。

(a)LSD算法效果

(b)改进LSD算法效果图7 改进前后LSD算法效果对比Fig.7 Comparison of results based on LSD and improved LSD algorithm

基于改进LSD算法提取的结构化约束特征点效果如图8所示，相对于粗定位效果，此时的结构化约束特征点定位更加准确，鲁棒性也更强。

(a)改进LSD算法提取特征直线效果

(b)基于改进LSD算法的结构化约束特征点提取效果图8 基于改进LSD算法提取结构化约束特征点Fig.8 Results of structural constrained feature points based on improved LSD

2.2 亚像素角点定位精度改进算法设计

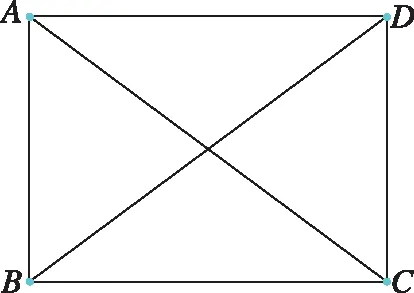
首先介绍亚像素角点检测算法原理，如图9所示，点为角点，点位于平滑区域内部，点处于边缘。

图9 角点特征Fig.9 Corner features

设点处的像素梯度为，在上述这两种情况下有

·(-)=0

(15)

·-·=0

(16)

转换成如式(17)所示的最小二乘形式

(17)

点的最小二乘解为

(18)

对于剩下的各个点，进行求和处理

(19)

为提高精确性，在最小二乘求解过程中引入高斯权重

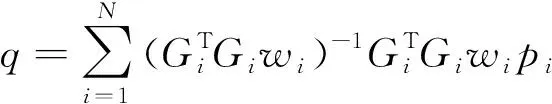
(20)

选取合适的点区域，提高角点的定位准确性。假设为初始角点，以为中心选取如图10所示的方形环形区域，区域内的每一点构成集合。

图10 pi点区域的选取Fig.10 Region of pi

由于噪声等干扰的存在，不能保证阴影区域内像素点梯度值计算正确，因此只选取像素梯度稳定可靠的像素点进行最小二乘迭代。

角点是通过基于改进LSD算法提取出的特征直线相交形成的，选取特征直线段上的像素点，以及垂直直线段方向上下邻域内的像素点，如图11所示，构成像素点集合。

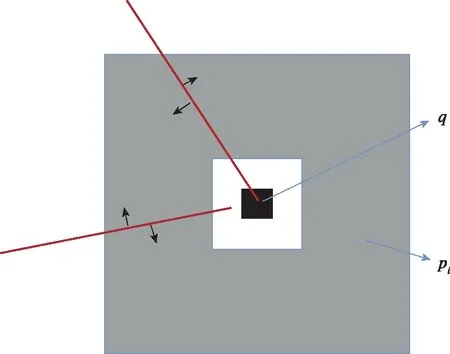
图11 像素点集合A示意图Fig.11 Diagram of pixel collection A

计算在直线段方向上的像素点梯度，以及垂直直线段方向上下邻域内的像素点梯度。集合中像素点(,)的灰度值为(,)，沿、方向的灰度梯度为(,)、(,)，计算其实际梯度角度为

(21)

将对应的特征直线斜率角度赋值给集合中对应的像素点，即给出了集合中每个像素点的理论梯度角度。

比较集合中像素点的理论梯度角度和实际梯度角度，如果2个角度的绝对值之差小于设置阈值，则认为该像素点的梯度可信。

为使像素点梯度更加准确，角度差值阈值的取值通常较为严格。这里认为像素点的理论梯度角度与实际梯度角度的差值在1°以内是可以接受的。

遍历集合中所有像素点，其中梯度可信的像素点组成集合。

最后，利用梯度可信的像素点进行最小二乘迭代，亚像素角点的定位精度会得到有效提高。

如图12所示，对比改进前后亚像素角点检测算法精度，以验证亚像素角点定位精度改进算法的有效性，表1所示为改进前后亚像素角点坐标与角点坐标真值对比。

(a)改进前

(b)改进后图12 改进前后亚像素角点检测算法效果对比Fig.12 Comparison of subpixel corner results

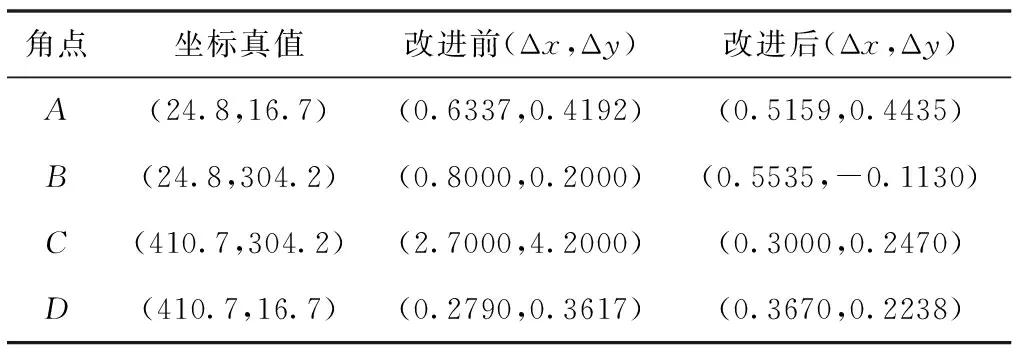
表1 改进前后亚像素角点坐标与坐标真值对比

改进前部分亚像素角点坐标与坐标真值存在较大偏差，甚至存在偏离4.2个像素的情况；而改进后的亚像素角点坐标在或方向的最大误差在0.5个像素左右，整体坐标偏移小于1个像素，定位精度得到有效提高。

图13所示为亚像素角点定位精度改进算法的应用效果图，在粗定位结构化约束特征点小区域内，选取像素梯度可信度高的点，用于改进亚像素角点的定位精度。

(a)特征直线及垂直相邻方向上的像素点

(b)梯度可信的像素点

(c)亚像素级结构化约束特征点图13 亚像素角点定位精度效果Fig.13 Results of improved subpixel corner positioning algorithm

3 仿真分析

利用SURF特征算法和ORB特征算法提取图像中的特征点，效果如图14所示。

(a)ORB特征算法

(b)SURF特征算法图14 传统特征点算法提取效果图Fig.14 Results of traditional feature point extraction algorithm

ORB特征仅考虑图像的灰度变化，SURF特征依赖于局部区域像素梯度方向，都没有利用到环境中存在的结构约束。传统特征点无法满足视觉着陆过程中相对定位的需要。

选取参数如表2所示，基于梯度一致性边缘检测算法提取图像中的结构化约束特征点。

表2 基于梯度一致性边缘检测算法提取结构化约束特征点参数选取

对以特征点为中心70×70大小的矩形区域，使用Shi-Tomasi角点检测算法提取强角点，实现对结构化约束特征点的粗定位，效果如图15所示。

图15 结构化约束特征点粗定位效果Fig.15 Rough positioning result of structural constrained feature points

选取参数如表3所示，基于改进LSD算法，提取以粗定位特征点为中心的100×100大小矩形区域内的结构化约束特征点。选取参数如表4所示，进行结构化约束特征点精定位。其中，窗口区域winSize和死区zeroSize的取值表示选取的点区域外方形大小为15×15，内方形大小为3×3。

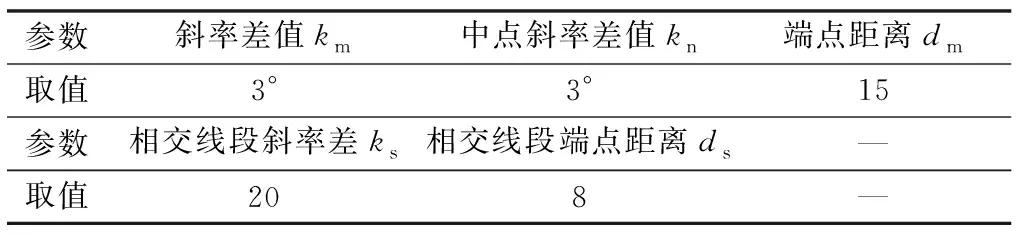
表3 基于改进LSD算法提取结构化约束特征点参数选取

表4 结构化约束特征点精定位参数选取

图16所示为结构化约束特征点精定位效果图。

图16 结构化约束特征点精定位效果Fig.16 Precise positioning result of structural constrained feature points

对比图16与图15,相较于粗定位而言，结构化约束特征点的精定位具有以下优点：

1)滤除了不能稳定存在的结构化约束特征点；

2)舍弃了重复检测到的多余特征点；

3)在原有特征点邻域内检测出更多稳定的结构化约束特征点；

4)将像素精度的结构化约束特征点提高到亚像素级精度。

对比图14和图16可以发现，ORB特征点分布存在聚集现象，且不稳定，无法满足视觉定位需求；SURF特征点具有较好的分布，但仍然没有利用到环境中固有的结构约束，不能保证特征点出现在结构化边缘。

相比较而言，结构化约束特征点是非合作特征点，具有更好的旋转不变性和尺度不变性，抗干扰能力更强。同时，亚像素级别的特征点能有效提高视觉定位的精度和可靠性。

更换降落平台场景，提取图像中的高精度结构化约束特征点，效果如图17所示。

图17 高精度结构化约束特征点提取效果Fig.17 Results of highly precise structural constrained feature points

以图16和图17所示的提取效果为例，能够说明论文算法可以有效获取稳定的高精度结构化约束特征点。

在实际应用中，应根据视觉定位需求，利用论文算法提取适合于导航定位的结构化约束特征点，结合这些标志角点的三维空间坐标，使用非迭代n点透视算法(Efficient Perspective-n-Point,EPnP)解算无人机相对于降落平台的相对位姿信息，实现视觉相对定位。

4 结论

本文针对视觉着陆过程中无人机的相对定位问题，选取环境中相交的特征直线段交点作为结构化约束特征点，该特征点能够有效抑制旋转、尺度、视角等不利因素的影响。本文主要结论如下：

1)设计基于梯度一致性的边缘检测算法，提取视觉图像中的结构化约束特征点，同时利用Shi-Tomasi角点检测算法，实现结构化约束特征点的粗定位；

2)在粗定位确定特征点区域的基础上，设计改进LSD算法，获取特征直线段的方程，进一步定位结构化约束特征点；

3)设计亚像素角点定位精度改进算法，将结构化约束特征点精确到亚像素级，有利于提高视觉相对定位的精度与可靠性。