毫米波通信定位一体化自组网资源分配技术

卢小峰，李越杰，陈若虚，殷本全

(西安电子科技大学通信工程学院，西安 710071)

0 引言

随着车联网、自动驾驶、工业控制等新兴业务的出现，针对无法获取全球定位系统(Global Positioning System，GPS)或蜂窝网基站信号场景，例如高密度城市、隧道等区域，实现高精度定位，给基于自组网的通信定位一体化研究带来了广阔的前景。自组网系统不依赖任何基础通信设施即可实现快速组网，同时部署难度低，成本效益高，能够满足不同场景下灵活、无缝的定位需求。

毫米波作为下一代通信系统的关键技术，能够提供高速通信，也能够应用于精确定位。因此，高度定向传输是毫米波通信系统中的一个理想特性，应用该特性，毫米波通信系统将具有较好的测距性能和角度估计精度，其中测距精度可达厘米到毫米级。同时，由于毫米波波束窄、波束定向强的性质，在通信过程中需要联同位置信息实现波束对终端的实时跟踪，以提高传输速率和定位精度。

在毫米波通信定位一体化系统中，通信与定位性能权衡问题中的时频资源分配得到了国内外学者广泛的研究。文献[2]研究了基于毫米波的通信定位一体化下时频资源分配策略，仿真了在时域和频域两种划分策略下单用户与多用户的定位误差性能，并讨论了这些策略的优缺点。文献[3]探讨了在城市道路单用户视距(Line of Sight，LoS)毫米波通信中通信速率和定位质量之间的权衡问题，通过增大波束训练开销提高费希尔矩阵(Fisher Information Matrix，FIM)的信息量，从而提升定位性能。文献[4]针对室外用户提出了一种基于定位的毫米波初始波束选择方案，设计了通信定位一体化帧结构，并推导了评价定位性能的指标：波束选择误差和波束不对准误差。文献[5]提出了协作无线网络中联合功率和带宽最优资源分配策略，并提出了泰勒线性近似迭代算法以解决该非凸优化问题。文献[6]对通信定位一体化的研究进行了归纳与展望，建立了一种多尺度非正交多址接入的新型共频带通信定位一体化信号模型，利用正交频分复用使不同定位用户的信号相互正交，从而降低多用户之间的干扰。文献[7]研究了mesh网中基于正交频分多址(Orthogonal Frequency Division Multiple Access，OFDMA)信道宽度自适应的时隙和子信道分配问题，提出了贪婪算法和遗传算法以获得资源分配的近似最优解，基于贪心算法设计了一种分布式媒体访问控制(Medium Access Control，MAC)协议。文献[8]研究了基于毫米波无人机mesh网下对移动无人机的波束追踪技术，从而提供可靠的高速率传输。文献[9]提出了毫米波LoS链路的新型聚簇算法，使用凸规划方法求解功率和子信道的联合分配问题，用乘法惩罚函数代替演绎惩罚函数，提高了优化算法的性能。文献[10]对毫米波多用户多载波系统中通信和定位性能之间的平衡进行了研究，推导了时分和频分框架下基于位置估计误差界(Position Estimation Error Bounds，PEB)和方位估计误差界(Orientation Estimation Error Bounds，OEB)的联合定位误差准则，并分析了单用户和多用户情况下最优波束形成优化问题。

上述关于毫米波的通信定位一体化研究主要集中在蜂窝网下，基站采用大规模天线阵列技术进行波束赋形，从而集中功率抵抗严重的路损与衰落。本文将在自组网下综合考虑设备硬件成本、实现复杂度、资源功耗等因素，在资源受限条件下进行合理的资源分配，以满足多用户通信和定位的联合需求，主要工作包括如下三方面：

1)构建了基于毫米波OFDMA的通信定位一体化自组网模型，采用联合时延、发射角(Angle of Departure，AoD)和到达角(Angle of Arrival，AoA)的锚节点定位技术，得到了基于位置估计的单用户克拉美罗下界，进一步推导出了联合PEB和OEB的OFDMA定位性能准则和衡量数据传输速率的通信性能准则。

2)联合考虑通信与定位性能，建立了OFDMA多用户通信定位一体化下的时频资源分配优化问题，并根据模型的特征，提出了基于广义Benders分解迭代的资源分配算法，解决了针对通信和定位最优子载波分配和最优时隙划分因子的求解问题。

3)仿真并分析了时隙划分因子对一体化系统中平均通信速率和定位性能的影响，探讨了两者性能之间的权衡关系，并验证了广义Benders分解算法应用于本文资源分配问题的有效性。

1 通信定位一体化模型

本节基于OFDMA构建了多用户毫米波通信定位一体化系统模型，并在该模型基础上推导了多用户定位性能准则和通信性能准则。

1.1 系统背景

在OFDMA多用户和毫米波的背景下，本文设计了图1所示的通信定位一体化模型，各个用户在该模型中共经历2个阶段，即组网阶段和服务阶段。其中表示组网阶段，在该阶段自组网内所有用户节点之间均被看作毫米波LoS链路，并通过控制帧完成时频资源的分配；表示服务阶段，在该阶段使用时隙划分因子将整个服务过程分割为2个子部分，分别对应不同服务内容，其中=(1-)用于通信服务，=用于定位服务。

图1 通信定位一体化框架Fig.1 Communication and positioning integrated framework

基于图1的通信定位一体化框架，本文将OFDMA系统的总带宽设置为，用户总数目设置为，子载波总数目设置为，发送天线和接收天线总数目分别设置为和。

图2 基于AoA、AoD、时延τ估计定位模型Fig.2 Location model based on AoA, AoD and delay τ estimation

从发送用户到接收用户的第个子载波的×复信道矩阵可表示为

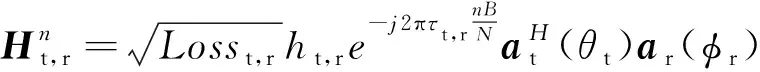
(1)

其中，为发射用户与接收用户之间的路径损耗;∈为信道系数;为毫米波链路时延;表示用户的AoD;表示接收用户的AoA。假设发射天线阵列和接收天线阵列为均匀线性阵列，天线单元个数为奇数，阵列质心为参考点，则发送端天线阵列响应可表示为

(2)

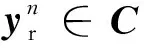
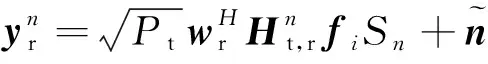
(3)

1.2 定位性能准则

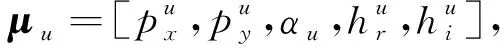
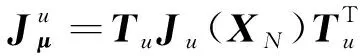
(4)

在服务阶段，每个用户分时进行通信服务和定位服务，若将各个用户分配的子载波集合定义为={,,…，}，则用户的子载波分配矩阵将表示为

,=diag(,1,,2,…,,)

(5)

假设本系统中毫米波波束定向时不受外界因素的干扰，即波束生成矩阵=最佳，那么OFDMA系统中用户的PEB和OEB将表示为

(6)

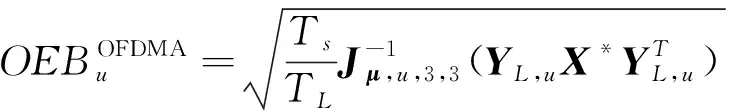
(7)

PEB指标是衡量到单锚节点距离位置测算的定位精度，OEB指标是衡量定位时方向角度的定位精度，将两者结合才能更全面地体现系统的定位精度，因此需要综合考虑PEB和OEB这2个指标，并将归一化联合推导后的结果定义为等效定位误差。

由式(6)和式(7)可以得到用户的等效定位误差为

(,)}

(8)

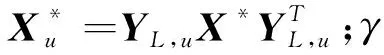
1.3 通信性能准则

用户在进行通信服务时,采用和定位服务相同的子载波分配方案，则OFDMA系统中用户的通信速率为

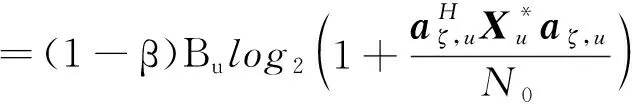
(9)

多用户平均速率为

(10)

其中，为用户的带宽，用户的通信速率取决于时隙划分因子和子载波分配矩阵,，时隙划分因子越小，通信服务的时间越短，用户通信速率越低，而,中非零分块矩阵越多，则划分给用户的子载波越多，通信速率越高。

2 优化问题及算法设计

由于通信服务和定位服务共享时频资源，两者性能的提升相互制约。因此,本节将研究时隙和子载波分配方式对通信与定位性能的影响，并建立优化问题模型，通过分析时隙划分因子探讨其折衷关系，解决优化问题。

2.1 优化问题

在OFDMA多用户系统中，由于信道的差异和子载波分配的不同，各个用户会表现出不同的定位误差，其中本系统的定位性能下界即为定位精度最差用户对应的等效定位误差。因此，在定位服务阶段，将定位优化问题设定为优化子载波分配矩阵,和时隙划分因子，使最差用户′定位误差最小化，并表示为

(11)

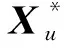
相应地，在通信服务阶段，根据通信性能准则，需要将多用户的平均速率作为优化目标。因此，将通信优化问题设定为调整子载波分配矩阵,和时隙划分因子，使系统中多用户平均速率最大，并表示为

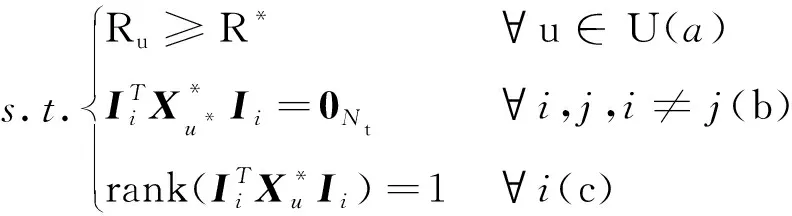
(12)

其中，表示多用户的最低速率门限。

在通信定位一体化的OFDMA系统中，需要在保障各用户最低通信速率的情况下，设定一种最优时频资源分配方案，使得所有用户的定位和通信性能最佳。因此，兼顾多用户的定位与通信需求，建立了通信定位一体化系统的总优化问题，并表示如下

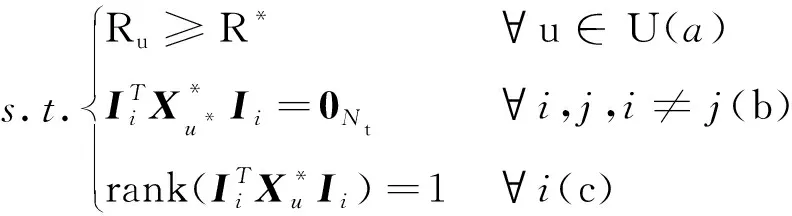
(13)

结合式(8)和式(10)，将优化问题(13)展开，总优化问题可重新表示为

(′,′)}+

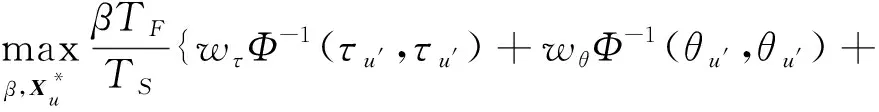
(14)

将该优化问题视为双层优化问题，分解为外层循环和内层循环进行下一步求解。

2.2 基于GBD法的算法设计

总优化问题为混合整数非线性规划问题，GBD(Generalized Benders Decomposition)算法被广泛应用于求解此类问题，因此在该节本文将结合GBD算法对总优化问题进行求解。

基于GBD算法，将时隙划分因子视为复杂变量，在每次可行循环中确定的值，并将总优化问题分解为主、子两个问题，其解分别对应总优化问题的上界和下界。在多次循环迭代求解中，通过添加新约束更新上界和下界的取值，当|上界-下界|≤条件成立或者达到最大迭代次数时，即认为在最后一次循环中求出的时隙划分因子和子载波分配结果为最优或近似最优解，其中为迭代过程中设定的收敛容许偏差常数。

固定复杂变量之后，总优化问题(13)变为初始子问题，表示为

(15)

其中,表示在第次循环中时隙划分因子的值，子问题的解对应原优化问题的上界，表示为

(′,′)}+

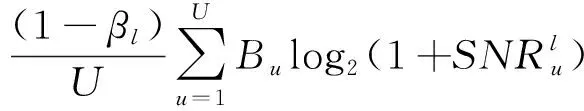
(16)

将下界表示为

=

(17)

其中，不小于初始化的下界值，下界则对应于主问题的解，那么可将主问题表示为

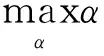
(18)

主问题(18)中的约束被称为Benders切，在每次迭代中不断更新并被作为主问题新的约束。求解主问题后，利用该次循环得到的最佳变量值在下次循环中求解子问题。重复上述操作，当上下界的差值小于设定的阈值时判定循环结束，得到原问题的最优解，算法流程见表1。在循环中，主问题与子问题皆为凸函数，可利用梯度下降法求解，其中有关主、子问题的凸性证明见附录A。

表1 基于GBD法的资源分配算法

3 仿真验证

本文中以30个用户节点和已知位置的锚节点作为基本的网络拓扑结构，在此基础上仿真了时频资源分配对定位和通信性能的影响以及性能间的权衡关系。

3.1 仿真参数设置

本文中毫米波通信系统采用的中心频率=60GHz，子载波间隔为150kHz，总功率平均分配在每个子载波上。毫米波自组网中用户均配备相同的天线阵列，天线单元数目均为30，单元间隔为05，10个毫米波帧组成为一个调度帧，调度帧帧长为10ms。

表2所示为OFDMA系统下通信与定位一体化具体仿真参数设置。

表2 OFDMA系统仿真参数

3.2 仿真结果分析

为了验证时隙划分因子对多用户通信速率和定位性能的影响，对多用户平均速率和定位误差PEB、OEB进行了仿真。图3所示为时隙划分因子=01,04,07,095时，多用户平均速率随信噪比的变化情况。

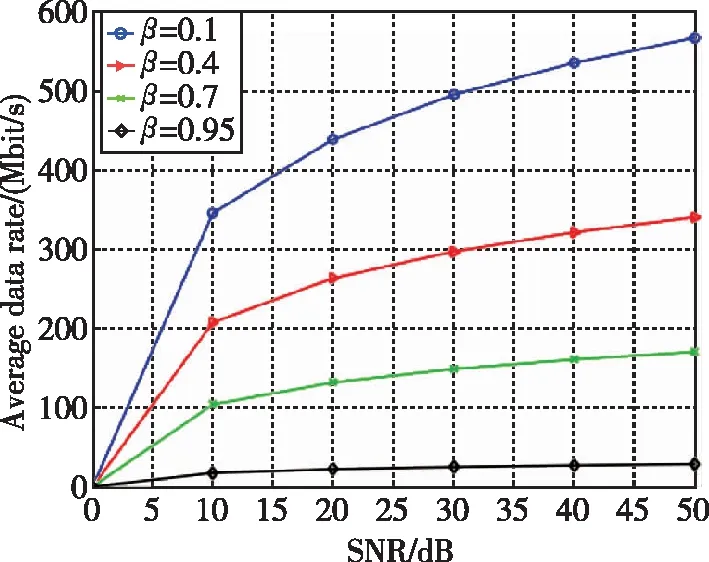
图3 β与平均数据速率Fig.3 β and the average data rate

从图3可以看得出，在信噪比一定的条件下，随着时隙划分因子的增大，多用户平均速率在降低，表明在帧长固定时，越大，分配给定位服务的时间越多，通信服务时间越少。

图4从时频角度出发，分别对多用户的PEB和OEB进行仿真，结果显示在带宽一定的情况下，随着时隙划分因子增大，PEB和OEB都在减小，说明随着增大，定位服务时间变长，定位性能得到提高。当固定时隙划分因子后，按照梯度设置了三种不同的带宽，通过对比可知，分配给用户的带宽越多，PEB和OEB越小，即用户的定位误差越小。可以看出，随着的增长，PEB和OEB的下降速度逐渐减缓，当由0.1增长至0.2的过程中，下降速度最大，往后随着的增长下降速度趋于平缓，这是由于定位时间的增长所带来对定位精度提升的收益趋于饱和，此时定位精度的提升主要依赖于系统带宽的增大。

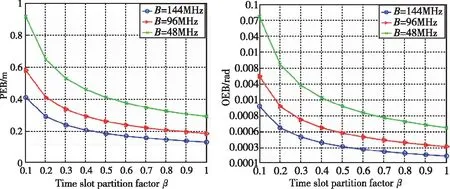
图4 PEB和OEB变化趋势图Fig.4 Trend chart of PEB and OEB

上述结果表明，时域和频域资源对多用户的定位性能均有影响，当分配时域资源对定位精度提升受限时，可以通过分配更多频域资源来解决。

然而，在通信定位一体化系统中，需要兼顾定位与通信性能，因此本文探讨了通信与定位性能的权衡关系。在同一资源分配策略下，图5为分别仿真了不同带宽下多用户的PEB和OEB与平均速率的关系权衡图。

图5 定位与通信性能的权衡图Fig.5 Trade-off performance between location and communication

在图5中，由于一体化系统中通信与定位是分时进行的，所以增加带宽可以同时提高用户数据速率和定位性能。当通信速率由100Mbit/s提升至300Mbit/s时，三种带宽下的PEB误差平均增大接近90%，OEB误差平均增大80%。这表明系统通过牺牲定位精度换取通信服务质量的提升，因为通信与定位两种服务对时域资源的分配是竞争关系。

随着时隙划分因子的变化，子载波的分配结果在每次迭代中都会发生变化，所以将每次迭代求得的时隙划分因子作为资源分配结果。在确定用户速率门限=100Mbit/s的情况下进行算法仿真，从图6中可以看出，在经过第7次迭代后，子问题和主问题的趋于一致，可认为当时隙划分因子约为0.35时可以满足最优化问题。

图6 GBD算法的迭代趋势Fig.6 Iterative trend of GBD algorithm

4 结论

本文在通信定位一体化背景下，结合OFDMA技术研究了毫米波自组网中多用户资源分配问题。

1)推导了联合PEB和OEB的等效定位误差为定位性能准则，将多用户平均数据速率作为通信性能准则。

2)兼顾通信和定位性能，建立了时频资源分配优化问题模型，针对最优时频分配提出了基于广义Benders分解的资源分配算法。

3)通过仿真验证了时频资源分配对通信与定位性能的影响及两者的权衡关系，为后续设计动态或自适应分配时频资源以满足用户不同业务需求的系统提供了理论依据。