扰动线运动对惯性系粗对准影响分析及优化方法

唐 苗, 刘 畅

(1.海军装备部驻北京地区第三军事代表室，北京 100074；2.北京自动化控制设备研究所，北京 100074)

0 引言

通过粗对准快速确定一个满足小角度假设的初始姿态矩阵，是进入精对准流程的前提条件，并且其对准精度、速度及对载体运动的约束大小直接影响了武器系统的响应快速性、环境适应性等作战能力。

目前常用的粗对准方法包括解析式粗对准和惯性系粗对准等。解析式粗对准通过加速度计和陀螺仪测量重力加速度以及地球自转角速度在载体坐标系的投影，利用双矢量定姿原理求解载体初始姿态矩阵。该方法要求载体静止，对扰动加速度和角速度较为敏感，因此使用十分受限。

惯性系粗对准由于不受载体自身角运动影响而得到广泛应用，最早由秦永元、严恭敏等提出，巧妙运用了惯性空间凝固假设，并采用对重力加速度积分的方法，消除了周期性的晃动干扰加速度影响。目前，国内外在惯性系粗对准算法方面已经取得了诸多成果。

虽然惯性系粗对准可以较好地抑制角运动的干扰，但也存在受线振动影响大的问题。赵长山等通过对重力加速度积分矢量进行线性最小二乘拟合，对粗对准过程中的扰动进行抑制，提高了在线振动环境下粗对准的精度。夏家和提出了一种采用分段积分和q-method方法提取足够多的加速度计量测信息，将姿态矩阵的求解问题转换为求解Wahba问题，提高了粗对准的鲁棒性。此外，文献[11-12]采用低通滤波器抑制线运动干扰；文献[13-15]采用滤波算法提高对准精度。

本文通过分析惯性系下重力加速度积分矢量及利用其构造的速度矢量矩阵的物理含义，定量地分析出扰动线运动对粗对准的影响；在此基础上给出了基于位移积分矢量构造定姿矢量矩阵的惯性系粗对准的优化方法，并通过试验数据仿真分析进行了验证。

1 惯性系粗对准分析

本文涉及的坐标系定义如下：

1)地理坐标系(系)：即北天东坐标系；

2)惯导体坐标系(系)：前上右坐标系；

3)地理惯性坐标系(系)：粗对准开始时刻地理坐标系凝固得到的惯性坐标系；

4)惯导惯性体坐标系(系)：粗对准开始时刻惯导体坐标系凝固得到的惯性坐标系。

为了便于分析，引入一个新的惯性坐标系系，则惯性系粗对准变为以下3个矩阵的求解过程

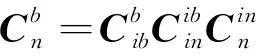
(1)

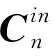
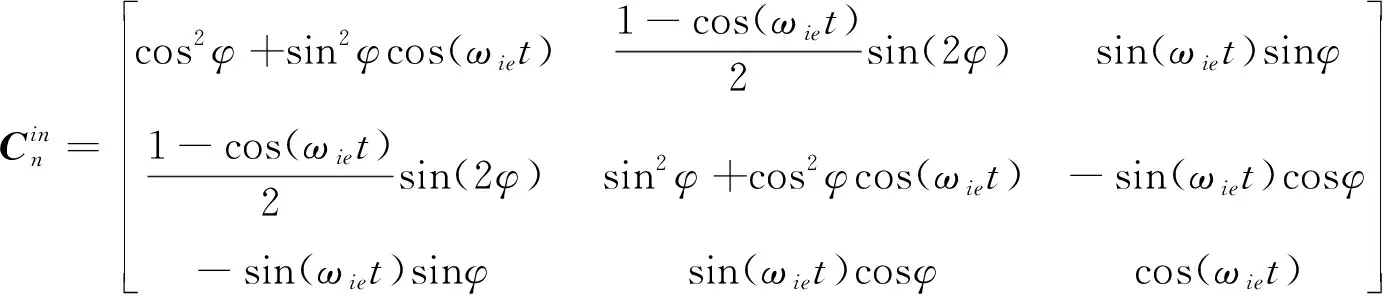
(2)

式中，为惯导系统当地纬度；为地球自转角速度；为粗对准时间。

由此，可得系下重力的矢量形式

(3)

当粗对准时间较短时，可认为是小量，从而式(3)可化简为

(4)

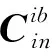
(5)

则重力在系下的投影可写为

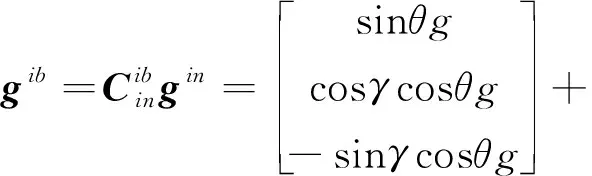
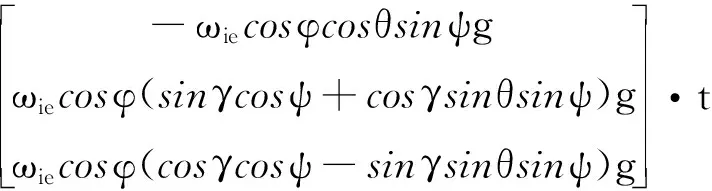
(6)

为防止扰动加速度及加表噪声等因素影响，对进行积分

(7)

从式(7)可以看出，一次项中包含了水平姿态信息，二次项中包含了航向信息。而当选取2个时间点的信息构建速度矢量矩阵时，相当于确定了的一次项和二次项(隐含粗对准开始时刻为0的条件)。假设在任意时刻的噪声水平相当时，选取的时间间隔越大，计算得到的一次项系数和二次项系数将越精确。因此,在选取时间点时通常选择粗对准时间及粗对准时间的一半，这样加上初始时刻三点间间隔最为合理。

在利用三点辨识一次项、二次项系数时，相当于解三元一次方程组

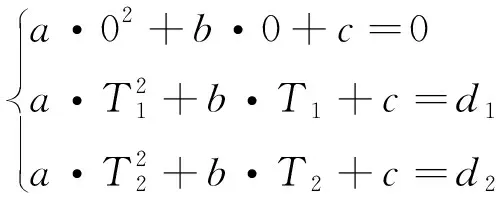
(8)

式中，、分别为粗对准时间长度的一半和粗对准时间；、分别为、时刻重力加速度矢量积分结果。

代入=2，可得

(9)

2 扰动线运动对粗对准影响分析

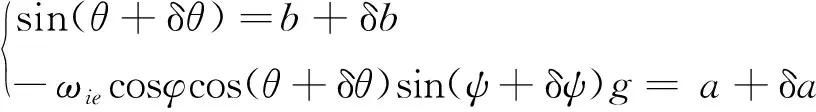
(10)

即

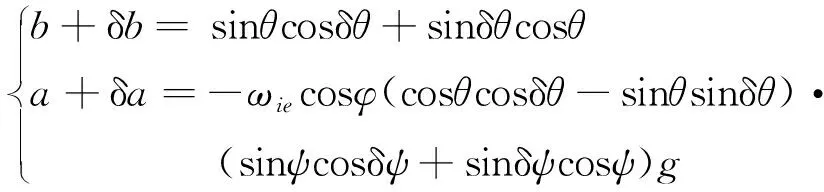
(11)

不妨假设载体姿态接近水平，则式(11)可进一步简化为

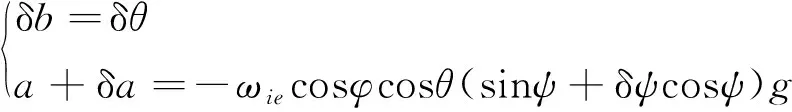
(12)

从而可得

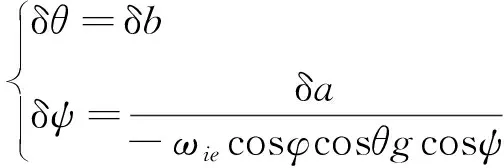
(13)

代入式(9),可得

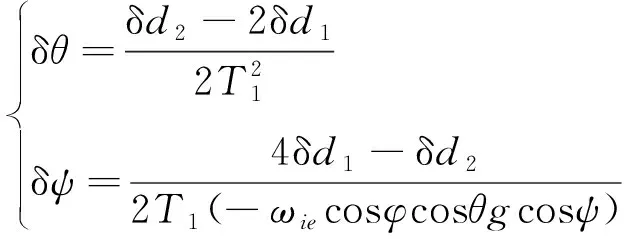
(14)

随后对某型中高精度捷联惯导系统静态对准数据进行仿真，惯导真实航向采用实际精对准结果180.48°，结果如表1所示。

表1 扰动速度对航向影响仿真结果

3 针对扰动线运动的粗对准优化方法

从前面的分析可以看出，扰动线运动对惯导系统粗对准精度的影响非常大，而惯导系统实际应用场景，如垂直发射、水面风浪及车辆行驶等动态环境下可能存在较大的真实速度，因此需要对惯性系粗对准算法进行一些改进。

惯性系粗对准算法在构造速度矢量矩阵时，只用了2个时间点的信息

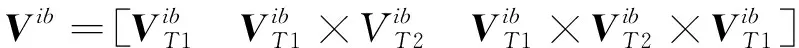
(15)

舍弃了其他时间点大量的速度积分信息，因此对扰动速度极其敏感。目前成熟的方法是通过最小二乘拟合重力积分矢量并用拟合参数重构速度矢量矩阵，该方法需要保存大量的数据信息，同时软件中增加了较多计算量。此外，该方法成立需满足一定前提条件：重力加速度积分矢量近似可表示为时间的多项式。从前文公式推导中可知，式(7)是在式(2)的基础上，即载体位置未发生变化的假定条件下推导得来。当载体处于运动状态时，由=+可知，若载体不是匀速直线运动，的积分结果就不是严格的时间的多项式形式。因此，若在运动状态下使用，需要动态条件远小于地球自转影响。以纬度60°为例，地表相对惯性系速度约为232m/s，因此载体运动速度应不大于23m/s。

考虑到实际对准期间线振动、角振动等条件下载体位置振动有限，本文采用对速度积分矢量进一步积分的方法抑制周期性的扰动加速度和线速度对粗对准的影响。

(16)

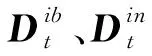
此外，在构造位移矢量矩阵时，利用3个时间点的位移积分信息

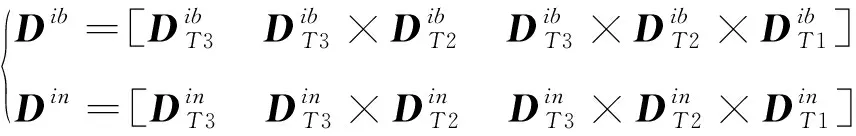
(17)

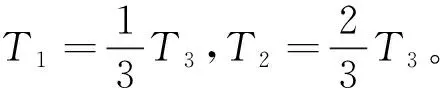
对于动态条件下动基座粗对准，当有里程计等外部速度信息输入时，可以通过式(18)进行积分

=

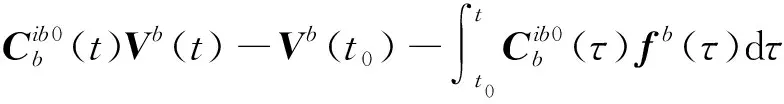
(18)

当有卫星等外界地理坐标系速度信息情况下，可以通过式(19)对进行积分

(19)

4 仿真验证

在上文某型捷联惯导系统静态对准数据的基础上增加一个周期0.3s、大小为1m/s的余弦加速度，再用两种粗对准方法进行仿真对比，结果如图1～图3所示。

图1 两种算法航向角对准结果Fig.1 Course angle results of two algorithms

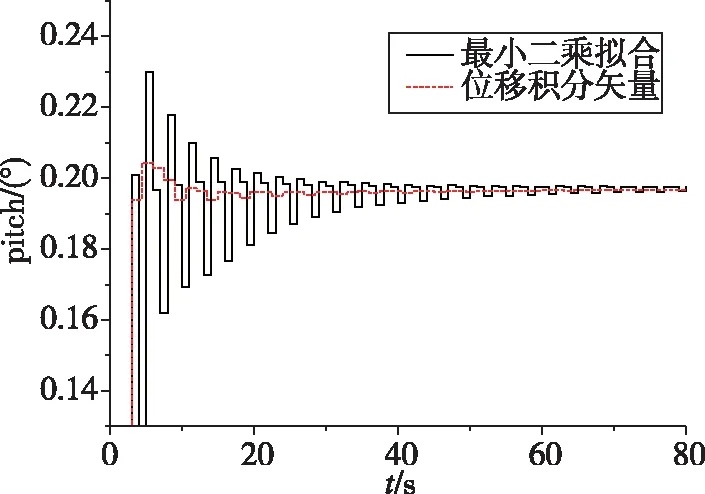
图2 两种算法俯仰角对准结果Fig.2 Pitch angle results of two algorithms

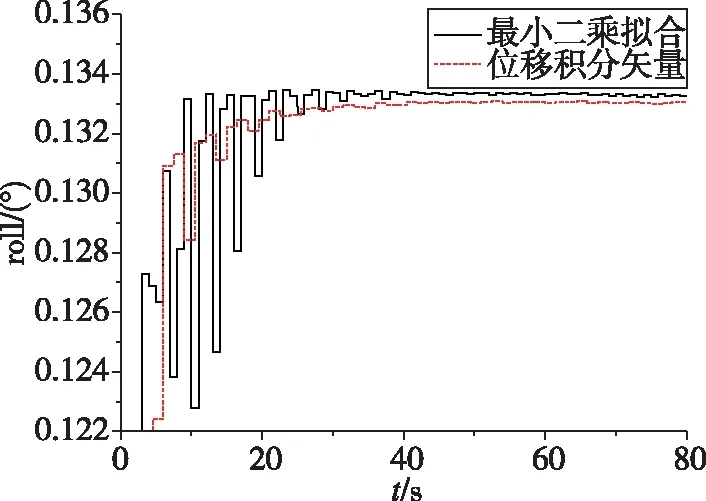
图3 两种算法滚动角对准结果Fig.3 Roll angle results of two algorithms

随后对该型惯导系统摇摆试验进行仿真，试验条件为摇摆幅度3°，摇摆频率1Hz，扰动线运动速度幅值约为0.35m/s，仿真结果如图4所示。

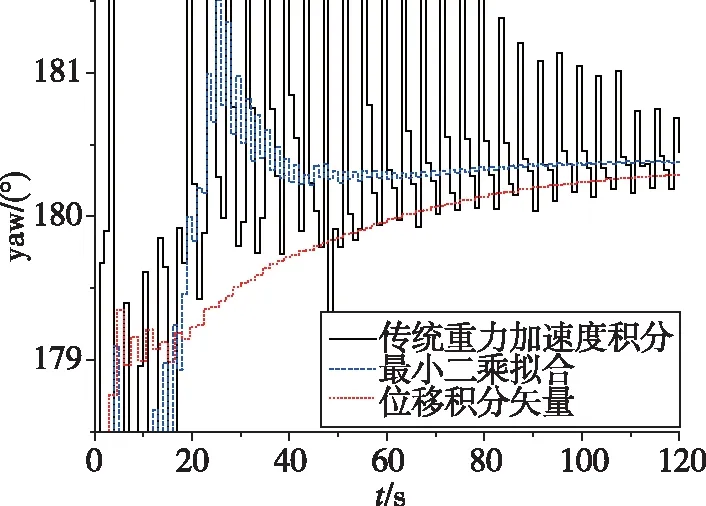
图4 摇摆试验仿真结果Fig.4 Simulation result of rolling test

从仿真结果可以看出，本文提出的位置积分矢量法虽然收敛速度比速度积分矢量最小二乘拟合法稍慢，但其对准结果的振幅受扰动线运动影响小，且精度与重力矢量积分法相比大幅提升，能够满足精对准使用要求。

5 结论

本文针对扰动线运动对粗对准精度影响较大的问题，提出了一种基于位移积分矢量的抗扰动粗对准算法，算法分析和仿真结果表明：

1)传统的惯性系抗扰动粗对准相当于用2个时间点的速度积分矢量进行最小二乘二次拟合，扰动线运动通过影响时间多次项参数辨识引入粗对准误差；

2)采用位移矢量积分的方式代替速度积分矢量进行最小二乘拟合，可以有效减少软件对处理器数据存储、运算速率的需求；

3)通过试验数据仿真分析可知，本文提出的基于位移积分矢量的抗扰动粗对准算法可有效抑制扰动线运动的影响，能较快收敛到满足精对准使用的粗对准精度。