基于B1c/B2a/B3I北斗三频实时高采样率动态PPP分析

郭秋英，刘传友，徐铭泽，黄守凯，毕京学，孙英君

(山东建筑大学测绘地理信息学院，济南 250101)

0 引言

北斗卫星导航系统(BeiDou Navigation Satellite System，BDS)是我国自主建设的全球卫星导航定位系统，能够提供三频乃至更多频的导航定位信号，能为全球导航卫星系统(Global Navigation Satellite System，GNSS)精密定位中的数据处理，如周跳探测与修复、模糊度固定等问题提供新的研究思路。GNSS精密单点定位(Precise Point Positioning，PPP)技术经过几十年的发展，其研究热点已经从事后、静态、双频定位转向实时、动态、多频定位。

为了满足实时PPP的需求，国际GNSS服务组织( International GNSS Service，IGS)于2013年成立实时服务(Real-Time Service，RTS)项目，并提供实时精密产品，众多学者也对各组织机构的实时产品进行了研究。我国也于2012年建立国际GNSS监测评估系统(international GNSS Monitoring & Assessment System，iGMAS)，能够提供多GNSS系统的精密星历钟差等产品。然而，对于实时PPP的研究大部分基于全球定位系统(Global Positioning System，GPS)、GLONASS和Galileo系统，并且对于BDS单系统也只是停留在对单频和双频方面的研究，对于单BDS三频实时PPP的研究仍然较少。目前，对于卫星定位信号的研究，主要集中在定位模型的改进、周跳探测与修复的优化以及提高模糊度的固定率等方面。除此之外，对于GPS而言，其卫星星座设计之初公开播发的只有双频信号，也限制了其在多频数据方面研究的发展。

目前，在北斗三号系统全面建成后，对基于北斗三号系统播发的新信号的三频实时动态PPP的定位性能研究较少的问题，本文针对单BDS系统，首先对两种常用的三频定位模型进行了推导，之后对iGMAS提供的超快速精密星历预报部分进行了精度和可靠性分析，并且基于此星历产品对北斗三号播发的新信号进行三频PPP处理，进而分析北斗三频动态PPP的定位性能。

1 三频PPP模型

1.1 数学模型

一般对于单系统单台接收机而言，其原始观测方程如下

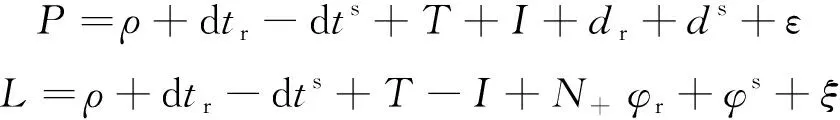
(1)

式中，s、r分别表示卫星端和接收机端；、分别为对应频率上的伪距和相位观测值；表示卫星到接收机的距离；d、d分别表示接收机和卫星的钟差；表示对流层延迟；表示电离层延迟；为载波相位模糊度；、、、分别表示接收机和卫星端的伪距硬件延迟、接收机和卫星端的相位硬件延迟；、分别表示伪距和载波相位观测值对应的测量噪声。对于天线相位中心改正、相对论效应、潮汐影响等均已通过模型改正。

1.1.1 三频非差非组合模型

非差非组合模型能够适用于单频、双频以及多频观测值的解算。在进行双频观测值PPP解算时，不同频率由于波长不同，在卫星内部的时延不同，导致伪距硬件延迟在不同频率上的偏差不同。因此，在观测方程中需要引入一个差分码偏差(Differential Code Bias，DCB)参数，其定义一般为

=-

(2)

式中，为差分码偏差；为频率的伪距硬件延迟；为频率的伪距硬件延迟。

目前，IGS和iGMAS提供的精密星历和钟差均是基于双频观测值计算生成的，一部分误差参数可通过参数规整被钟差吸收，另一部分误差参数可以并入电离层延迟和模糊度中，从而减少待估参数，提高解算效率。为了表示方便，进行如下定义

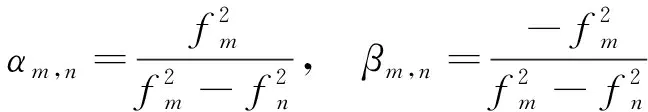
(3)

式中，、为定位解算使用的频率号(,=1,2,3)；表示相对应的载波相位频率值；和表示无电离层组合系数因子；IF、IF分别表示接收机和卫星端经双频信号组合后形成的无电离层组合伪距硬件延迟。

在进行三频观测值PPP解算时，除了要引入DCB参数外，由于在第3个频率上的伪距码偏差不能被电离层完全吸收，因此在第3个频率伪距观测方程中还需要引入一个伪距频间偏差(Inter-Frequency Bias，IFB)参数，三频非差非组合观测方程的IFB可表示为

=··(-)-
IF+IF+-

(4)

由于iGMAS的精密钟差产品中包含了第一频率和第二频率的无电离层组合形式的伪距硬件延迟，无法与精密卫星钟差分离，并且与电离层参数具有相关性，因此可以将卫星端伪距硬件延迟纳入到卫星钟差和电离层延迟中；对于接收机端的伪距硬件延迟，由于与接收机钟差、模糊度具有相关性，因此纳入到接收机钟差中。为了保持观测方程中参数的一致性，通过调整参数，三频非组合的线性观测方程可表示为

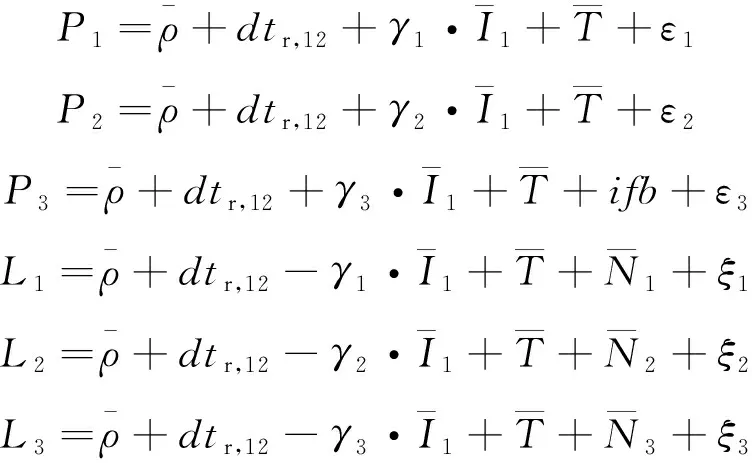
(5)

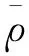
1.1.2 三频无电离层两两组合模型

由于IGS和iGMAS等组织提供的精密卫星钟差都包含了卫星端的伪距硬件延迟，因此对于使用北斗系统B1-B2频率进行双频无电离层组合PPP解算时，卫星端的伪距硬件延迟可以被精密卫星钟差吸收，接收机端的硬件延迟可以被接收机钟差参数吸收。然而，当利用北斗B1-B3频率进行双频无电离层组合PPP解算时，B1-B3的无电离层组合伪距硬件延迟不能被精密卫星钟差吸收，在接收机端也不同于B1-B2无电离层组合伪距硬件延迟的影响。

为了保持2个无电离层组合观测方程中参数定义的一致性，仍需引入一个伪距频间偏差参数，其定义如下

=IF-IF+IF-IF

(6)

除此之外，相位硬件延迟被模糊度参数吸收，导致模糊度参数也不再具有整数特性。因此，三频无电离层两两组合观测方程可表示为

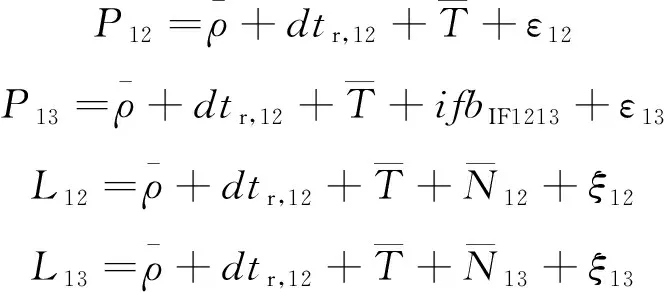
(7)

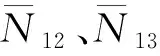
1.2 随机模型

随机模型是用于描述观测值质量精度的，由于低高度角会导致更大的多路径效应等观测噪声，因此需要对观测值的精度进行量化，一般采用高度角随机模型。

假设不同频率观测值之间相互独立，且不同频率上的伪距观测值和载波观测值的测量噪声均相同，则三频非差非组合PPP随机模型可表示为

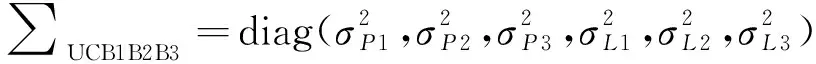
(8)

式中，|=sin()，为观测噪声，对于载波相位观测值，一般设置为0.003m，对于伪距观测值，则设置为0.3～3.0m；为卫星高度角。

根据方差-协方差传播律，得到三频无电离层两两组合的随机模型为

∑=

(9)

2 超快速精密星历的获取与分析

实时精密单点定位的主要难点在于难以获得实时精确的轨道和钟差，现阶段有如下方法可以获得较高精度的实时轨道和钟差产品：1)使用IGS或iGMAS数据分析中心提供的超快速精密星历，但是IGS分析中心提供的超快速精密星历并不包含精密钟差产品；2)使用RTS提供的实时数据流改正轨道和钟差，但是，大部分机构并不提供BDS的轨道和钟差改正数。

2.1 超快速精密星历获取

本文基于iGMAS提供的超快速精密星历中的预测部分，使用BDS-3播发的新信号B1c和B2a，以及BDS-2、BDS-3共同播发的B3I信号，进行三频精密单点定位实验研究。值得注意的是，iGMAS提供的精密星历有两种：1)基于B1I/B3I频点计算得到的轨道和钟差产品；2)基于B1c/B2a频点计算得到的轨道和钟差产品。然而，基于B1c/B2a频点计算的精密星历中大部分BDS-3卫星没有可靠的钟差产品，因此，本文将使用基于B1I/B3I频点计算得到的轨道和钟差产品。

iGMAS提供的超快速精密星历产品是以北斗时为基准计算的，为了方便计算和之后的分析比较，需要将超快速精密星历产品的时间转换到GPS时，有

=+14+

(10)

表示GPS时和北斗时维持的协调世界时之间的微小量差值。对于精度要求不高时，可忽略不计；对于高精度的定位而言，轨道产品可采用10阶拉格朗日内插，钟差产品可采用线性内插。

2.2 超快速精密星历质量分析

对于超快速精密星历，首先要对其精度和可靠性进行分析。本文通过对比iGMAS超快速精密星历和最终精密星历，分析iGMAS提供的超快速精密星历的精度和稳定度，为之后的实验分析提供依据。

首先计算了iGMAS超快速精密预测部分轨道与最终精密轨道的偏差，以及超快速精密预测部分钟差与最终精密轨道钟差的二次差(以C19卫星作为基准星)，统计在超快速精密星历下每颗卫星的均方根(Root Mean Square, RMS)值，分析BDS-3系统的卫星轨道和钟差精度，如图1所示，其轨道与钟差RMS值计算方法如下

图1 北斗三号(各)卫星的轨道和钟差均方根误差Fig.1 All satellites’ orbit and clock RMS

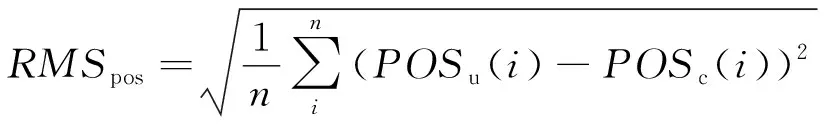
(11)

式中，、分别表示超快速精密星历预报部分和最终精密星历的卫星轨道位置；表示钟差二次差；表示总历元数。

由图1分析可知，在超快速精密星历预测部分,BDS-3各卫星的轨道均方根误差精度均能精确到8cm以内，且大部分分布在3.70～7.80cm之间；对于超快速精密星历预测部分的钟差均方根误差精度能精确到1.26ns以内，且大部分分布在1.10～1.25ns之间。

其次，计算了iGMAS的超快速精密预报部分轨道和钟差与最终精密轨道和钟差随时间变化的差值，如图2所示。

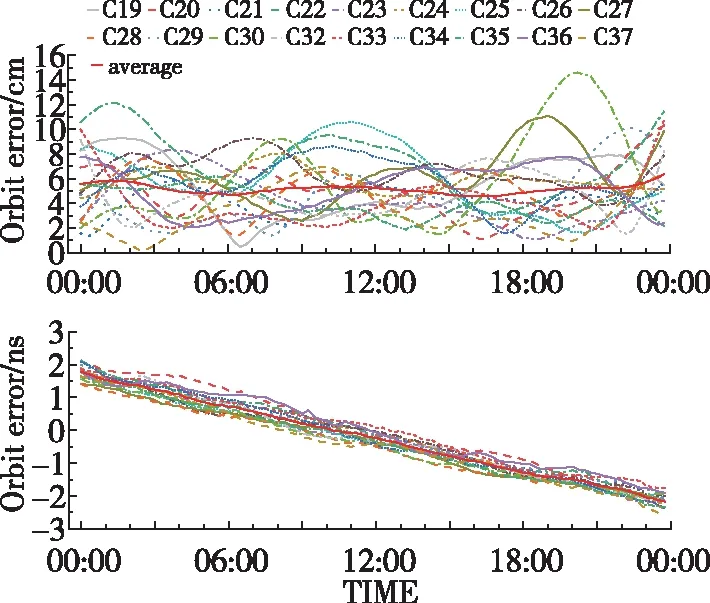
图2 各卫星轨道和钟差偏差随时间变化趋势Fig.2 The trend of the orbit error and clock deviation of each satellite over time

由图2可知，BDS-3各卫星的轨道偏差大部分分布在1.2～12.1cm以内，其各卫星轨道偏差的均值随时间变化的稳定度相对较好；钟差随时间近似呈线性变化，且变化相对稳定，无误差突变现象。

3 北斗三频实时动态PPP分析

3.1 实时PPP数据的获取及处理策略

本文选取了2020年12月26日于山东建筑大学的CORS站(JNJZ站)采集的1s采样率数据，基于iGMAS超快速精密星历和钟差产品的预测部分，使用Net_Diff数据处理软件对实测的BDS-3数据进行三频实时动态精密单点定位实验。以一周时间的GPS+BDS双系统载波双频相对定位结果的均值作为参考真值，分析在不同定位方案下的精密单点定位性能。其中，测站坐标作为白噪声参数模拟动态定位，高度角设置为8°，周跳探测方法使用Geometry_Free组合+Melbourne_Wubeena组合，模糊度解算使用浮点解，对流层估计使用Global_Pressure_and_Te-mprature_2_Wet+Saastamounien model+Vienna_Mapping_Functions_1组合，其余如地球自转改正、潮汐效应、天线相位中心偏差均使用已有精确模型改正。

对于采集的原始观测值数据，将其平均分成8个时段，对每个时段均进行重新解算。实验制定了四种定位方案，如表1所示。

表1 定位方案

3.2 PPP实验结果精度分析

首先，分析了解算时的可见卫星数和位置精度因子(Position Dilution of Precision, PDOP)值，如图3所示。

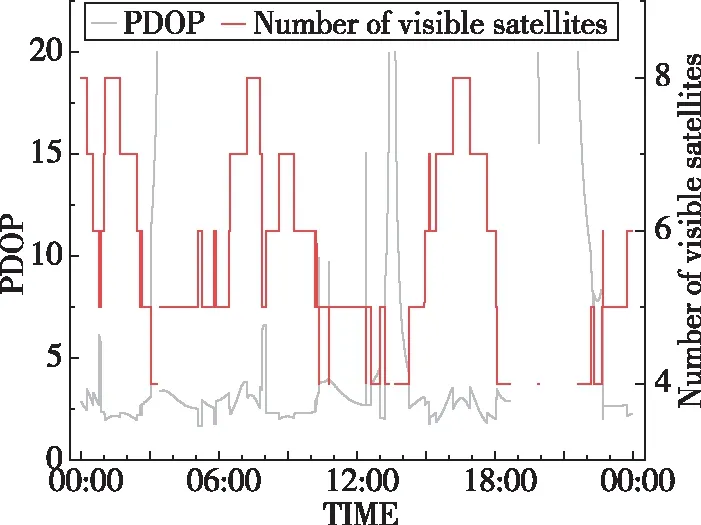
图3 可见卫星数及PDOP值随时间变化Fig.3 The number of visible satellites and the PDOP changes with time

由图3的可见卫星数和PDOP值分析可知，2020年12月26日JNJZ站BDS-3可见卫星数最多能够达到8颗(不包含C38及以后的卫星)，但是在19:00～22:00之间有部分时间数据不能解算。由图3及数据处理文件分析可知，其原因是部分卫星在设置的观测截止高度角以下，导致可见卫星数少于4颗。对于PDOP值，在不考虑实验数据解算失败的情况下，其大部分分布在2.0～8.5之间。

之后，分析了四种定位方案的定位结果在NEU方向上的定位精度，如图4所示；统计了各个定位方案的收敛比例(达到收敛精度的定位次数在总定位次数中的占比)、平均收敛时间(首次定位及之后30个历元的定位结果偏差均在分米以内视为收敛)以及收敛后的平均RMS值，如表2所示。

表2 各方案定位性能统计

由图4和表2分析，可以得出：

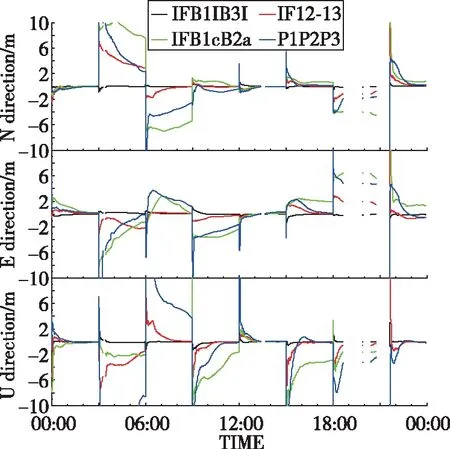
图4 各定位方案在NEU方向的偏差Fig.4 The deviation of each positioning scheme in NEU

1)两种三频定位方案相对于IFB1cB2a定位方案在NEU方向上均有更快的收敛速度、更高的定位精度，且IF12-13方案略优于P1P2P3方案；但在使用Net_Diff软件进行数据解算中发现，IF12-13方案定位解算时间较P1P2P3方案短，其原因是P1P2P3定位方案待估参数多于IF12-13定位方案。

2)值得注意的是，IFB1IB3I双频方案在收敛时间和定位精度上均优于两种三频定位方案，收敛性也相对更好。

3)结合图3，在可见卫星数大于5及PDOP值小于5.0时，IFB1IB3I、IF12-13和P1P2P3方案均有较好的定位精度和较快的收敛速度。

4 结束语

本文通过推导两种三频定位模型，制定了基于B1cB2aB3I信号的四种定位方案，基于JNJD站采集的1s采样率观测值数据，利用超快速精密星历预测部分，进行高采样率三频实时动态PPP实验，对实验结果的PDOP值、定位精度及收敛速度进行分析，得出以下结论：

1)基于B1IB3I信号计算得到的超快速精密轨道预报部分相较于其事后最终精密轨道的误差，大部分能精确到12cm以内，钟差大部分能优于1.26ns。

2)四种定位方案中IFB1IB3I定位性能最优，其后依次是IF12-13、P1P2P3、IFB1cB2a。其原因是使用的超快速精密星历是基于B1I和B3I信号计算生成的，与IFB1IB3I定位方案匹配度更好。

3)除此之外，由于P1P2P3方案定位模型中待估参数多于IF12-13方案，使得P1P2P3方案的解算时间高于IF12-13方案。

目前，北斗三号系统已经全面建成，但是对于北斗新信号的研究仍然处在发展阶段，由于对北斗三号系统支持的软硬件以及相匹配的精密星历等产品较少，也限制了本文对北斗三号新信号的研究，这也是以后需要进一步研究的重点。