例析分类思想融入初中数学教学

成安平

（宁波市实验学校，浙江 宁波 315010）

初中数学中的分类讨论问题，是近年来中考压轴题的一个热点，也是教学的难点。由于压轴题综合性比较强，学生在考虑问题的时候，会因为条件或结论不唯一确定而出现的几种可能性，引起重复或者遗漏的情况，这给学生带来了很大的困惑。初二学生由于知识的延伸，已经逐步接触分类思想，但是八年级教材特别是几何与函数，学生第一次系统地认识分类思想，他们习惯凭感觉去解决实际问题，往往会对所有可能出现的情况考虑得不够完整，逻辑思维不够严密。所以这就要求初二年级教师做好分类思想的启蒙教育，在设计教学过程渗透核心素养即逻辑推理的培养，抓住分类讨论的动因，把握住分类的标准，做到分类时条理清楚、标准一致，对所学的概念、定理、法则、公式等基础知识及背景进行透彻的分析，对教材进行更深的挖掘，帮助学生灵活地掌握知识，促进学生从感性思维到理性思维的升华。

一、初见分类

等腰三角形是浙教版八年级上《特殊三角形》的内容。两条边相等就可以判定一个三角形是等腰三角形，可能条件不唯一，所以学生往往只凭几个特殊的值来解决问题，容易遗漏。教师讲解时要抓住等腰三角形的判定定理，从边的两两相等来分三类情况讨论。例1 如下图，在平面坐标系中，ABCO 为正方形，已知点B 的坐标为（4，4），点P 的坐标为（3，3），当三角板直角顶点与P 重合时，一条直角边与x 轴交于点E，另一条直角边与y 轴交于点F，在三角板绕点P 旋转过程中，若△POE 为等腰三角形，则点 F 的坐标为________。

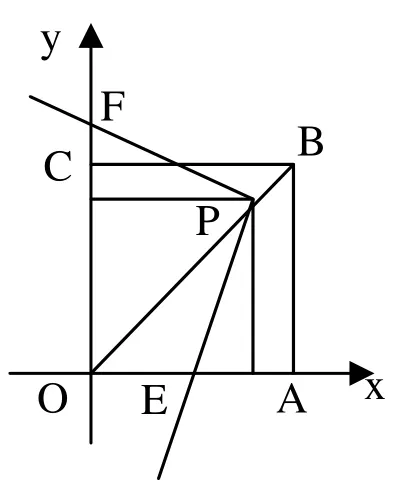
分析：由于图中有正方形，所以学生的考虑到（0，0）（0，3）这两种情况。

答：等腰三角形要分三类讨论。

（1）当PE=PO 时，F（0，0）

（2）当PE=OE 时，F（0，3）

等腰三角形分类，是学生学习分类讨论思想的起步，教师要给一定的练习加以巩固，并且能够多鼓励学生，多倾听不同的声音。

二、架构分类

直角三角形是浙教版八年级上《特殊三角形》的内容。只要一个角是直角就可以判定一个三角形是直角三角形，条件减少难确定。这样的题型往往和相似三角形或者特殊的直角三角形结合来增加确定条件。例2 如下图，等边△OAE，边长为2，E 在y 轴上，O 为坐标原点，正方形ABCD，B、C 在x 轴上。

（1）求经过A、D 两点抛物线的对称轴。（2）是否存在点P，满足点P 的纵坐标大于点D 的纵坐标，且以A、D、P 为顶点的三角形与△AOB 相似（不包括全等），若存在点P，请直接写出点P 的坐标；若不存在，请说明理由。（3）正方形ABCD 绕点A 按逆时针方向旋转，当BD 所在直线与AE 所在直线垂直时，求直线BD 的解析式。

本题的第（2）小题和（3）小题都是要用分类讨论的思想解决问题，其中第二小题隐含了直角三角形和相似三角型的结合，有比较大的难度。教师讲解是要分两步进行。第一，分析三角形△AOB 是一个含有30°的直角三角形；第二，从△AOB 的三个内角分别为直角分三类讨论，并考虑到相似三角形角对应相等。

学生往往会遗漏一些条件，从而只找到几个结果。教师讲解时要分两步，首先确定其中一个是直角，其次对每一个锐角进行分类。教师在课堂上要架构起分类的思想，不断进行数学建模的启蒙、训练和巩固。

三、深究分类

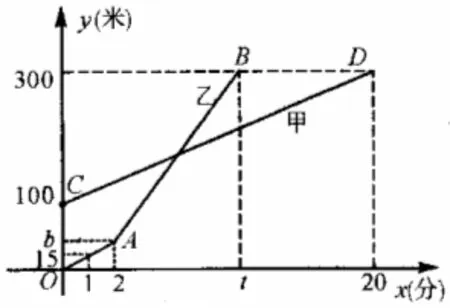
一次函数分段讨论是浙教版八年级下最后一章最后一节《课题学习》的内容，教师和学生比较容易忽视本节的内容，教师在讲解时要注意挖掘教材，让学生认识到一次函数的自变量的取值范围是任何实数，但是对于实际问题还要考虑到符合实际的每一段的范围。例3，甲乙两人同时登西山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图像如下图所示，根据图像所提供的信息解答下列问题：

（1）甲登山的速度是每分钟_______米，乙在A地提速时距地面的高度b为________米。

（2）若乙提速后，乙的速度是甲登山速度的3 倍，请分别求出甲、乙二人登山全过程中，登山时距地面的高度y（米）与登山时间x（分）之间的函数关系式。

（3）登山多长时间时，乙追上了甲？此时乙距A地的高度为多少米？

解:（1）10，30

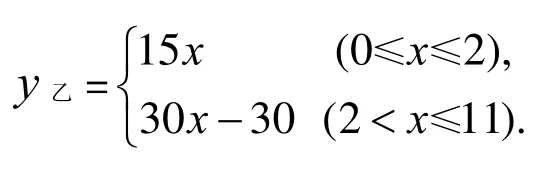
∴登山6.5 分钟时乙追上甲。此时乙距A地高度为165-30=135（米）。

教师要有意识地留出较多时间让学生去探索，选择解决问题的方法，然后引导学生用图像法解决问题，在备课时要注意对课后练习的挖掘，为以后的分类思想打好基础。

四、锤炼分类

长方体的表面展开图是浙教版八年级上第三章《直棱柱》第二节的内容，教学分为两个方面，即要培养动手能力，又要锻炼空间想象能力，且由于不同的裁剪方式会有不同的表面展开图。在讲解时，要充分调动学生的积极性，通过游戏的方式让学生尽可能地把所有的情况都写出来，教师最后进行总结归纳，并且给以一定的配套练习，使得展开图在学生脑中根深蒂固，并且渗透分类思想。例4 是探索研究如下图，把一张长10cm，宽8cm 的矩形硬纸板的四周各剪去一个同样大小的正方形，再折合成一个无盖的长方体盒子（纸板的厚度忽略不计）。

（1）要使长方体盒子的底面积为48cm2，那么剪去的正方形的边长为多少？（2）你感到折合而成的长方体盒子的侧面积会不会有更大的情况？如果有，请你求出最大值和此时剪去的正方形的边长；如果没有，请你说明理由。（3）如果把矩形硬纸板的四周分别剪去2 个同样大小的正方形和2 个同样形状、同样大小的矩形，然后折合成一个有盖的长方体盒子，是否有侧面积最大的情况；如果有，请你求出最大值和此时剪去的正方形的边长；如果没有，请你说明理由。

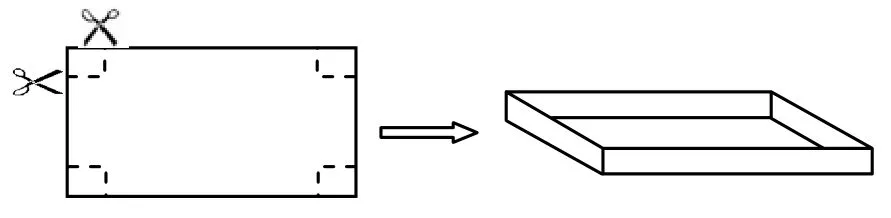
分析：本题的原型来源于浙教版八年级下《一元二次方程》应用的第二节内容。一元二次方程的应用是本章的难点，而这个折纸盒的问题需要学生应用八年级上的内容建立适当的数学模型，即动手又动脑，要求比较高。教师要深度挖掘教材，鼓励学生自主探索，采取分组学习的教学方法，利用变式训练，把所有的可能性的情况都归纳分析，真正做到来源于书本而高于书本。

答：（1）设正方形的边长为xcm，则。

解得x1=8（不合题意，舍去），x2=1。

∴剪去的正方形的边长为1cm。

通过观察、验证直接写出正确结果给3分。

（2）有侧面积最大的情况。设正方形的边长为xcm，盒子的侧面积为ycm2，则y与x的函数关系式为：

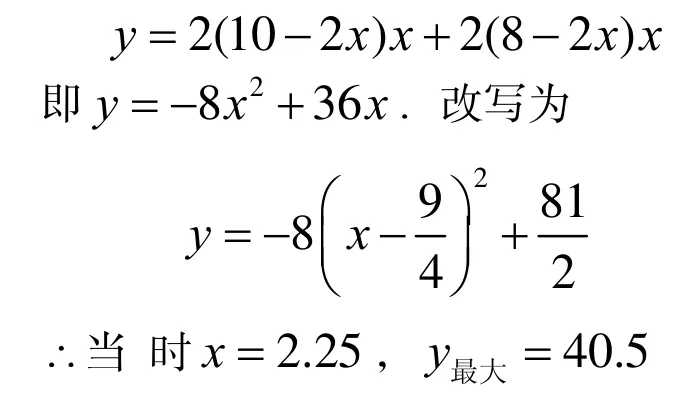
即当剪去的正方形的边长为2.25cm 时，长方体盒子的侧面积最大为40.5cm2。

（3）有侧面积最大的情况。设正方形的边长为xcm，盒子的侧面积为ycm2。若按下图1

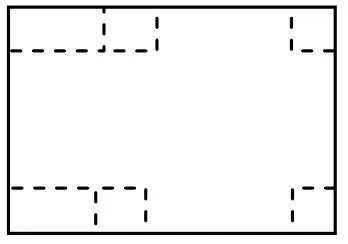
图1

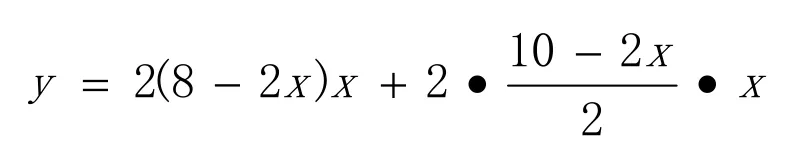
所示的方法剪折，则y与x的函数关系式为：

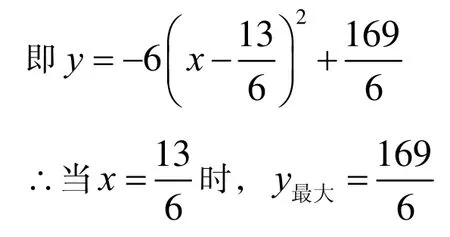
若按图2 所示的方法剪折，则y与x的函数关系式为：

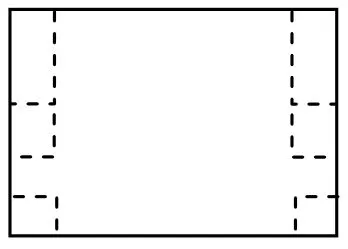
图2

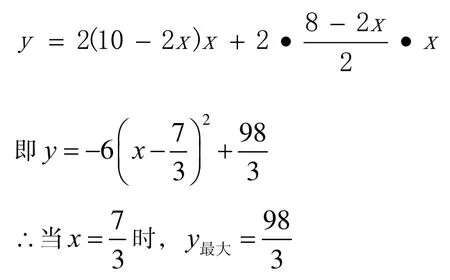
比较以上两种剪折方法可知，按上图2 所示的方法剪折得到的盒子侧面积最大，即当剪去的正方形的边长为cm 时，折成的有盖长方体盒子的侧面积最大，最大面积为cm2。

初中的学习中，分类讨论的思想没有作为独立章节呈现，而是渗透在各个章节中。教师分析教材时在思想上要充分意识到教材中可能涉及的分类思想，特别是对于初二学生，根据初中学生的特点，教学中遵照循序渐进、逐步深化的原则，并采用灵活多变和有效的教学手段来实施分类讨论方法的启蒙教学，培养和发展学生思维的条理性、缜密性，从而提高学生分析问题和解决问题的能力。在授课时要给学生分析分类讨论时注意的二个问题。第一，用同一标准进行分类。分类应按同一标准进行，即每次分类不能同时使用几个不同的根据。如果划分的标准不同，则划分的结果也不同。第二，分类讨论的步骤。分类讨论时应先明确其讨论的对象及讨论对象的取值范围，其次选择正确的分类标准，进行合理分类，再次逐类讨论解决，最后归纳并作出总结。不断渗透逻辑推理、数学建模、数学运算等初中数学核心素养的培养。

分类讨论问题充满了数学辩证思想，它是逻辑划分思想在解决数学问题时的体运用，掌握好这类问题对提高综合学习能力会有很大的帮助，它既有利于培养学生的创新精神与探索精神，又有利于培养学生严谨、求实的科学态度。