图形与几何中数学语言表达能力发展路径——以人教版教材《平面图形面积的复习》一课为例

□ 袁春胭 王 霞

即将颁布的新的数学课程标准中提出了“三会”核心素养：会用数学的眼光观察现实世界，会用数学的思维思考现实世界，会用数学的语言表达现实世界。笔者以人教版教材五年级上册《平面图形面积的复习》一课为例，以在场景中理解数学语言、在对话中规范数学表达、在应用中创生数学语言，助力学生在图形与几何领域的理解与运用，促进其空间观念的发展，以适应学生进一步学习和终身发展的需要。

一、在场景中理解数学语言

图形与几何是小学数学教学中的重要组成部分，对培养学生空间想象、几何直观、推理能力等具有关键性的作用。在图形与几何教学中注重学生数学语言表达能力的培养，能让学生更好地用数学的眼光观察周围世界，有助于学生对几何图形进行深度理解和规范表达，从而发展空间观念。

（一）创设数学对话情境，激发学生理解数学语言的兴趣

学生在图形与几何内容的学习中遇到的困难往往是“语言”未过关，不理解题意，不会按题意画出合适的图形。有的题目虽然学生有解题思路，但因为语言匮乏，往往写不清、道不明。

【教学片段1】

师：同学们，今天我们来复习平面图形的面积。（师板书课题并出示图1）这些图形认识吧？（生答：认识）要计算它们的面积，你们有没有什么问题？

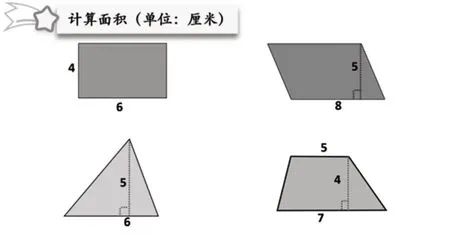
图1

师：好！谁来算第一个？

生：长方形的面积是4×6=24（平方厘米）。

师：同意吗？（生答：同意）平行四边形呢？

生：平行四边形的面积是8×5=40（平方厘米）。

师：嗯。真快！那么第三个呢？

生：三角形的面积是5×6÷2=15（平方厘米）。

师：嗯！很厉害！最后一个梯形呢？

生：梯形的面积是（5+7）×4÷2=24（平方厘米）。

（评析：在课堂中创设计算简单平面图形面积的对话场景，让学生在运用公式解决问题的过程中提炼公式，从而有效地回顾旧知，理解知识，激发学习的兴趣。）

（二）建构推理表达情境，提高学生逻辑思维能力

教师在教学图形与几何这一内容时，要充分展示图形语言的优越性，加强数学语言的表达，让学生能够精确表达图形的空间形式，在推导一些特殊图形周长、面积、体积计算方法的过程中，感悟数学度量方法，逐步形成量感和推理意识，促进空间能力的发展。

【教学片段2】

师：如图 2 所示，梯形ABCD的高是 4 厘米，上底AB为 3 厘米，下底CD为 9 厘米。如果梯形的高不变，上底减少，下底同时增加同样的长度，面积会变吗？

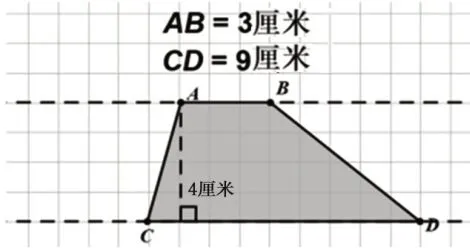
图2

生：不会变。如果上底减少的长度与下底增加的长度相等，那么上底+下底的和不变。因此梯形的面积（上底+下底）×高÷2不变。

师：如果上底继续变短，下底同时增加同样的长度，那么当梯形的上底变为0 的时候，是一个什么样的图形？它的面积是多少？

生：梯形变成三角形了（如图3）。它的面积和原来的梯形是一样的。这时相当于原来的梯形上底减少 3 厘米，为 0 厘米，下底增加 3 厘米，为 12 厘米，上底+下底的和依旧不变。三角形可以看成是上底为0的梯形。

师：如果梯形的上底和下底一个增加，另一个减少相同的长度，梯形还可能“变”成哪些图形？这些图形的面积都可以用梯形的面积公式计算吗？

生：如果上底增加，下底减少，梯形可以“变”成平行四边形，平行四边形的面积可以用底×高计算，也可以用（上底+下底）×高÷2 计算。大家看，梯形中的“上底+下底”的和是平行四边形的底的2 倍，再÷2，梯形面积公式与平行四边形面积公式求得的结果是一样的（如图4）。

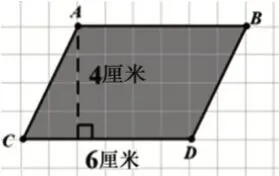
图4

（评析：在巩固延伸环节，教师以梯形为核心，引导学生尝试从新的角度勾连不同平面图形的面积计算方法。学生在数学表达的过程中，逐步厘清了这些平面图形面积之间的深层联系，有效提高了推理意识，拓宽了思路，更好地解决了问题。）

二、在对话中规范数学表达

笛卡尔曾经说过：“没有任何东西比几何图形更容易印入脑际，因此，用这种方式来表达事物是非常有益的。”在数学学习中，教师应引导学生学会用符号、数据、模型等数学语言进行规范表达。数学语言是进行数学交流的重要载体，能严谨、准确地表达数学世界，提升数学思维。

【教学片段3】

师：前面大家把梯形“变”成了三角形，“变”成了平行四边形，如果继续“变”，但要保持面积不变，你还想到可以怎么变吗？

生：还可以把平行四边形通过剪拼变成长方形。长方形的长就是平行四边形的底，长方形的宽就是平行四边形的高。根据长方形面积公式“长×宽”计算，面积不会变化。我们学平行四边形面积的时候就是这样做的。

生：原来的平行四边形底是6 厘米，高是4 厘米。反过来变成底是4 厘米，高是6 厘米的平行四边形也是可以的。

生：数据还可以继续变化，可以变成底是12厘米，高是2厘米，或者底是24厘米，高是1厘米都行。

师：看来，只要底和高的乘积是24，都可以。

师：刚刚大家一起回顾了梯形、三角形、平行四边形和长方形的面积公式，如果在几个公式中只记住一个，你会选择哪一个？

生：记住梯形的就可以了，因为其他几个图形都可以转化为梯形来计算。

（评析：在学生用数学语言表达的过程中，教师要合理把握教学的重难点，对于图形与几何中蕴含的深意要层层挖掘。以上教学中，教师抓住“如果在几个公式中只记住一个，你会选择哪一个”这个问题展开交流讨论，让学生在规范数学语言表达的过程中不断理解数学知识，分析思维能力得以进一步发展。）

三、在应用中创生数学语言

数学本身具有很强的逻辑性和抽象性，运用规范严谨的数学语言，有利于培养学生独立思考、富于见解的思维品质，并在今后的图形问题解决中保持严谨的思维习惯。

【教学片段4】

在画等积图形环节中，为了让学生画一画不同的图形，回顾长方形、平行四边形、三角形、梯形这些学过的平面图形的面积计算公式的推导过程，教师通过课件出示图5。

图5

在交流环节，教师分别展示学生作品，引导学生依次回顾长方形、平行四边形、三角形、梯形的面积计算公式的推导过程，从而帮助学生更好地巩固面积公式，从更深的层次上来明白面积公式推导的意义。

（评析：通过这样的数学语言表达，可以简约、精确地描述自然现象、科学情境和日常生活中的数量关系与空间形式。教师设置开放的情境，让学生对图形几何的本质有了更深入的理解，也同时帮助学生进一步理解其本质意义，以发展学生的空间观念和推理能力。）

数学语言的表达能力不是一蹴而就的。教师要立足课标与教材，在课堂教学中重视发展学生的数学语言表达能力，有意识地创设数学对话情境，激发学生理解数学语言的兴趣和提高学生逻辑推理的能力；在对话交流中，师生共同进行设疑、质疑、释疑的数学思辨活动；在互动开放的环节中，进行图形间的有效联结和应用。如此，才能促使学生逐步学会用数学的眼光观察现实世界、用数学的思维思考现实世界、用数学的语言表达现实世界，真正实现提升数学核心素养的教学愿景。