《空间向量及其运算》（第1课时）教学设计

陈坤美

摘 要：本节课主要类比平面向量学习空间向量的概念和线性运算，主要包括七个教学环节.通过创设问题情境、设置问题串引导学生参与探究活动;借助立体几何图形帮助学生分析和理解概念;注重渗透类比、数形结合、特殊与一般、转化与化归的思想.

关键词：空间向量;教学设计;类比思想

中图分类号：G632   文献标识码：A   文章编号：1008-0333（2022）06-0020-04

1 内容解析

《空间向量及其运算》是人教A版《普通高中教科书·数学（选择性必修）》第一册（以下简称“教科书”）第一章《空间向量与立体几何》的第一节内容，包括“空间向量及其线性运算”和“空间向量的数量积运算”两小节内容，其中第1课时“空间向量及其线性运算”要学习的核心知识有：空间向量的概念;零向量、单位向量、相等向量、相反向量、共线向量、共面向量;空間向量的加法、减法以及数乘运算.这些核心知识是后续学习空间向量基本定理、空间向量运算的坐标表示、应用空间向量解决立体几何图形位置关系与度量关系的基石.

本节课的重点是：空间向量及其相关概念，空间向量的加法、减法以及数乘运算.

本节课的难点是：空间向量加法结合律的证明，用向量方法解决立体几何问题.

2 学情分析

在学习本节课内容之前，学生已在人教A版必修第二册中学习了《平面向量及其应用》和《立体几何初步》内容.熟悉了平面向量的基本研究思路与框架即“实际背景→基本概念→向量运算（线性运算、数量积）→向量基本定理及坐标表示→向量的应用”，这也是研究和学习空间向量的基本路线.

3 教学目标

（1）了解空间向量的实际背景;理解空间向量及相关概念;掌握空间向量的加法、减法和数乘运算.

（2）经历由平面向量的概念、运算推广到空间向量的过程;通过空间向量加法结合律的证明体会维数增加对向量推广带来的变化;在证明空间四点共面的过程中明析立体几何中向量方法的“三步曲”：用空间向量表示立体几何图形→向量运算→对运算结果进行几何解释.

（3）在借助几何图形解释空间向量相关概念中进一步发展直观想象核心素养，领悟数形结合的思想方法;结合空间向量的概念、运算与运算律证明四点共面的过程中提升数学运算和逻辑推理能力;从平面向量推广得到空间向量、空间向量问题转化为平面向量问题的过程中提升数学抽象素养，领悟类比、特殊与一般、转化与化归等思想.

4 教学策略

本节课采用创设问题情境，设置问题链引导学生类比平面向量层层深入学习空间向量的概念、线性运算、运算律和位置关系等内容.学生通过自主探究、生生交流、师生互动等教学活动参与学习过程，突破学习中的难点和疑点.利用几何画板、PPT等教学软件绘制图形、平移图形、展示图片，借助几何直观图形帮助学生分析和理解概念.

5 教学过程

5.1 创设情境，导入新课

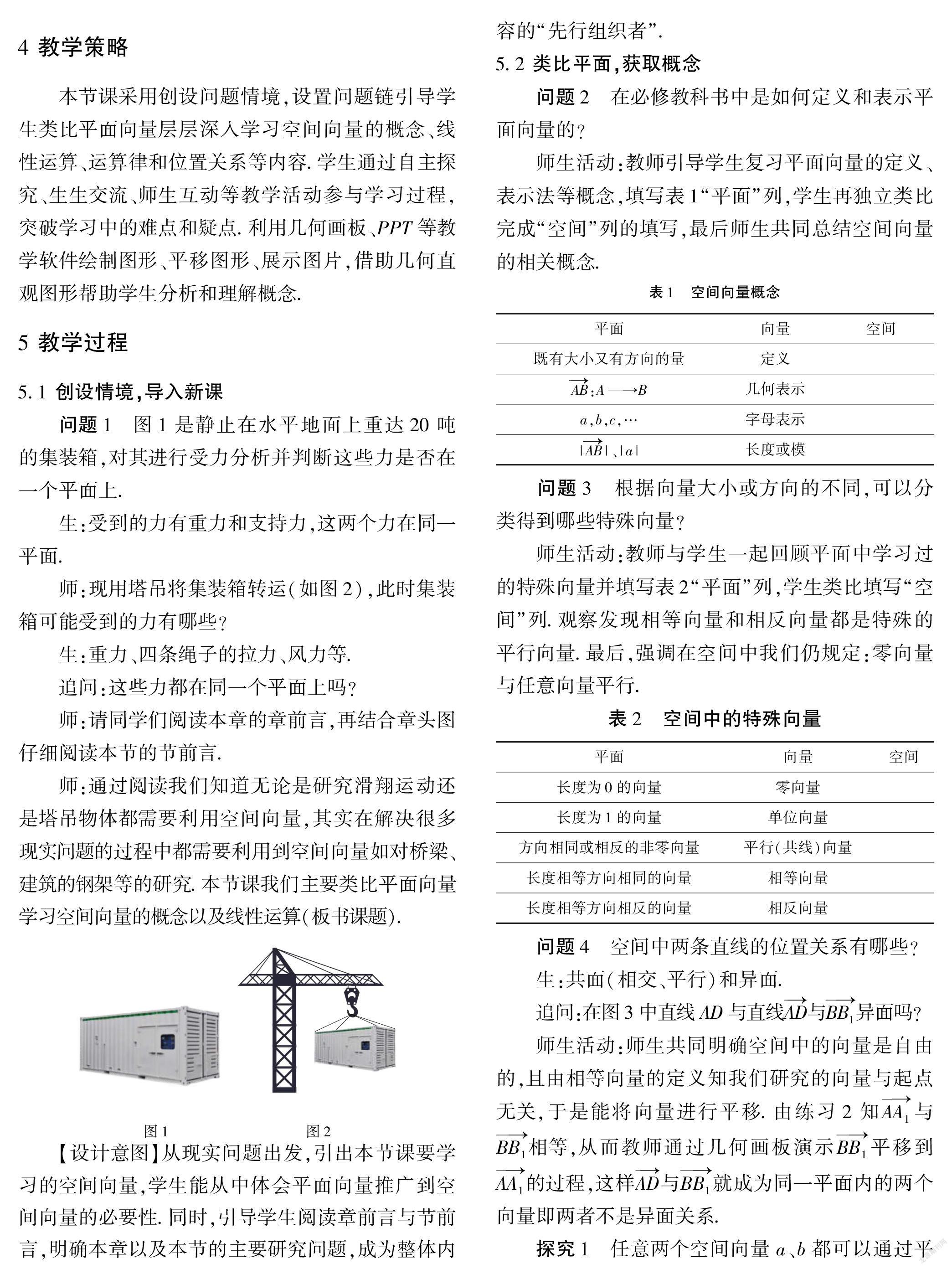
问题1 图1是静止在水平地面上重达20吨的集装箱，对其进行受力分析并判断这些力是否在一个平面上.

生：受到的力有重力和支持力，这两个力在同一平面.

师：现用塔吊将集装箱转运（如图2），此时集装箱可能受到的力有哪些？

生：重力、四条绳子的拉力、风力等.

追问：这些力都在同一个平面上吗？

师：请同学们阅读本章的章前言，再结合章头图仔细阅读本节的节前言.

师：通过阅读我们知道无论是研究滑翔运动还是塔吊物体都需要利用空间向量，其实在解决很多现实问题的过程中都需要利用到空间向量如对桥梁、建筑的钢架等的研究.本节课我们主要类比平面向量学习空间向量的概念以及线性运算（板书课题）.

【设计意图】从现实问题出发，引出本节课要学习的空间向量，学生能从中体会平面向量推广到空间向量的必要性.同时，引导学生阅读章前言与节前言，明确本章以及本节的主要研究问题，成为整体内容的“先行组织者”.

5.2 类比平面，获取概念

问题2 在必修教科书中是如何定义和表示平面向量的？

师生活动：教师引导学生复习平面向量的定义、表示法等概念，填写表1“平面”列，学生再独立类比完成“空间”列的填写，最后师生共同总结空间向量的相关概念.

问题3 根据向量大小或方向的不同，可以分类得到哪些特殊向量？

师生活动：教师与学生一起回顾平面中学习过的特殊向量并填写表2“平面”列，学生类比填写“空间”列.观察发现相等向量和相反向量都是特殊的平行向量.最后，强调在空间中我们仍规定：零向量与任意向量平行.

问题4 空间中两条直线的位置关系有哪些？

生：共面（相交、平行）和异面.

追问：在图3中直线AD与直线AD与BB1异面吗？

师生活动：师生共同明确空间中的向量是自由的，且由相等向量的定义知我们研究的向量与起点无关，于是能将向量进行平移.由练习2知AA1与BB1相等，从而教师通过几何画板演示BB1平移到AA1的过程，这样AD与BB1就成为同一平面内的两个向量即两者不是异面关系.

探究1 任意两个空间向量a、b都可以通过平移成为同一平面内的两个向量吗？

师生活动：师生结合教科书“图1.1-3”画图分析，同时利用几何画板做向量平移过程的动态演示.说明其中的依据和本质是“两条相交直线确定一个平面，故起点重合的两个不共线向量可以确定一个平面”.

【设计意图】立足立体几何知识，为学生学习空间向量找到知识生长点;利用信息技术实现师生更深入的交流互动，课堂内容更加生动直观.

5.3 类比运算，证运算律

师：在学习了平面向量的概念之后，我们类比数的运算学习了它的线性运算，现在又知道空间向量的运算可以转化为平面向量的运算，那能否把平面向量的线性运算推广到空间呢？

师生活动：结合教科书中“图1.1-4”和“图1.1-5”对空间向量的加法、减法、数乘运算的运算法则进行直观理解.

问题5 平面向量加法运算和数乘运算满足的运算律有哪些？

生：平面向量的加法运算满足交换律和结合律，数乘运算满足结合律和分配律.

追问1：这些运算律对空间向量成立吗？

探究2 如何证明空间向量加法的结合律？这与证明平面向量的结合律有何不同？

师生活动：师生共同回顾平面向量加法结合律的证明（如图4）.

因为

AD=

AB+BD=AB+（BC+CD）=a+（b+c）;

AD=

Ac+cD=（AB+BC）+CD=（a+b）+c）;

所以a+b+c=a+b+c.

对于空间向量，若三个向量在同一平面则转化为平面情形用图4证明;若三个向量不在同一平面则类比平面画出图5来证明，同时结合图5归纳总结得到以下结论：

（1）首尾相接的若干向量之和等于第一个向量的起点指向最后一个向量的终点所表示的向量.

（2）当首尾相接的若干向量围成一个封闭图形时，它们的和为零向量.

（3）两个向量相加的平行四边形法则在空间仍然成立.

【设计意图】通过复习平面向量加法结合律的证明为空间中的证明给予一定的启发.由于维数的增加，三个向量可能在同一个平面也可能不在，因此要分类讨论进行证明，画图分析能帮助学生突破学习难点.

5.4 交流互动，共探关系

5.4.1 空间向量共线的充要条件

探究3 任意两个空间向量a（a≠0）与b，a∥b的充要条件是什么？

问题6 a与λa有什么位置关系？

问题7 若b=λa，a与b有什么位置关系？

问题8 平面中，向量a（a≠0）与b共线的充要条件是什么？

【设计意图】基于向量数乘的定义和平面向量共线的充要条件，设置三个问题引导学生得到两个空间向量共线的充要条件.

师：我们知道两点可以确定一条直线，且两点构成的有向线段可以表示向量，图6、图7所示是由A、B两点确定的同一条直线l，思考

AB与BA有什么关系？

生：它们互为相反向量、共线（平行）向量.

师：也就是说它们的主要差异是方向相反，那方向相反对直线l有什么影响？

生：这说明直线l有两个方向.

师：总结得非常好！实际上，我们将AB、BA都称为直线l的方向向量.一般地，在直线l上任取非零向量a（如图8），我们把与向量a平行的非零向量称为直线l的方向向量.

师：如图9，O为方向向量a的起点，P为直线l上的任意一点，结合向量共线的充要条件你能得到什么？

生：存在实数λ，使OP=λa.

师生总结：直线可以由其上一点和它的方向向量决定.

【设计意图】在师生的一问一答和交流互动中有序推进课堂，紧扣直线的定义将向量知识串联，学生在参与分析、回答、解决问题的过程中实现对知识的深化理解.同时，注重符号语言、向量语言、图形語言三种语言的互补和转化.5.4.2 空间向量共面的充要条件

师：在前面练习1中，部分同学找出的三个向量从图中看似乎是不在同一平面，但老师告诉大家它们实际是在同一平面的，现在就作出合理的解释.

师：任意两个空间向量总是共面，三个向量可能共面也可能不共面，那么什么情况下三个向量共面呢？

探究4 对于任意两个不共线的空间向量

a，b，向量p与向量a，b共面的充要条件是什么？

问题9 当向量p与向量a，b共面时，它们之间有怎样的关系？（提示学生结合平面向量基本定理思考）

生：存在唯一的一对实数x，y，使p=xa+yb.

5.5 反思回顾，自主总结

（1）这节课主要学习了哪些内容？与平面向量相关概念有何联系与区别？

（2）空间向量的线性运算满足哪些运算律？如何证明加法的结合律？

（3）空间向量共线、共面的充要条件分别是什么？

（4）用空间向量解决立体几何问题的“三步曲”是什么？

（5）本节课主要涉及了哪几种数学思想？

【设计意图】围绕本节课的重点、难点、

思想方法进行总结反思，促进学生把握本节课的知识结构.5.6 布置作业，达标检测

（1）教科书第5页练习2、4、5.

【设计意图】考查空间向量的线性运算.

（2）下列命题中不正确命题的序号为

①若空间向量a、b满足|a|=|b|，则a=b.

②两个空间向量相等，则它们的起点相同，终点也相同.

③向量AB与BA的长度相等.

④如果a∥b，b∥c，则a∥c.

【设计意图】辨析空间向量的相关概念.

（3）设e1、e2是空间中两个不共线的向量，已知

AB=2e1+te2，CB=e1+3e12，CD

=2e1-e2，且A、B、D三点共线，求t的值.

【设计意图】考查空间向量共线的充要条件及其运算.

（4）证明：空间中P，A，B，C，四点共面的充要条件是存在有序实数对（x，y，z），使得对空间中任意一点O都有OP=xOA+yOB+zOC（其中x+y+z=1）.

【设计意图】此题是对练习4的变式训练，加深学生对空间向量共面的理解，满足部分学生想多学一点数学的学习需求.

参考文献：

[1] 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020.

[2] 人民教育出版社，课程教材研究所，中学数学课程教材研究开发中心.普通高中教科书教师教学用书数学选择性必修第一册（A版）[M].北京：人民教育出版社，2020：13.

[3] 刘长明.基于核心素养的“空间向量与立体几何”教材设计与教学思考[J].中学数学教学参考，2020（31）：6-9.

[责任编辑：李 璟]