非交换剩余格上的n重PMTL滤子及其刻画
左卫兵, 张一旎
(华北水利水电大学 数学与统计学院, 河南 郑州 450046)
为给不确定性信息处理理论提供可靠且合理的逻辑基础,许多学者研究了各种非经典逻辑系统.同时,作为非经典逻辑系统的语义系统的各种逻辑代数也被广泛研究,如剩余格、MTL代数、BL代数、MV代数和R0代数等[1-5],以及它们的各种非交换版本,如非交换剩余格、伪MTL代数、伪BL代数、伪MV代数等[6-10].这些逻辑代数中剩余格和非交换剩余格是最基本且最重要的代数结构,其他逻辑代数均是它们的特殊情况.
在逻辑代数的研究中,滤子理论起到了非常重要的作用.目前,在剩余格、非交换剩余格以及其他逻辑代数中,各种特殊滤子已被引入,如正规滤子、布尔滤子、蕴涵滤子、正蕴涵滤子、奇异滤子等[11-19],并获得了许多重要结果.
受文献[20-21]的启发,本文在非交换剩余格上引入n重PMTL滤子的概念,得到这类滤子的一系列刻画,提出n重PMTL代数的定义,从n重PMTL滤子的角度证明n重PMTL代数的若干特征定理,并通过提出n重素滤子的定义,给出n重PMTL代数的另一种刻画.
1 预备知识
定义 1.1[22]代数系统

称为非交换剩余格,如果:
1) (L,∧,∨,0,1)为有界格;
2) (L,⊗,1)是非交换幺半群;
3) 对任意x,y,z∈L,则

在非交换剩余格L,对∀x∈L,定义

定义 1.2[7]非交换剩余格L若满足

则称L为伪MTL代数.
定义 1.3[8]一个伪MTL代数L若满足

则称L为伪BL代数.
引理 1.1[22]设L是非交换剩余格,那么对于任意x,y,z∈L,以下性质成立:








9)x⊗(y∨z)=(x⊗y)∨(x⊗z),(y∨z)⊗x=(y⊗x)∨(z⊗x);
10)x→(y∨z)≥(x→y)∨(x→z)和
(y∧z)→x≥(y→x)∨(z→y),


11) (y→z)⊗(x→y)≤x→z和

12)x⊗y≤x∧y,特别地,x2≤x.
定义 1.4[22]设F为非交换剩余格L的非空子集,如果:
1)x∈F,y∈F⟹x⊗y∈F;
2)x∈F,x≤y⟹y∈F,则称F为非交换剩余格L的滤子.
引理 1.2[22]设F为非交换剩余格L的非空子集,则以下条件等价:
1)F是L的滤子;
2) 1∈F,x,y∈L,(x∈F,x→y∈F)⟹y∈F;

2 n重PMTL滤子
定义 2.1设F为非交换剩余格L的滤子,若对任何
x,y∈L,n∈N+,
有
(xn→y)∨(y→x)∈F,
且

则称F为L的n重PMTL滤子.
注意到,当n=1且F为正规滤子时,1重PMTL滤子就是文献[23]所提到的PMTL滤子.
下面例子表明非交换剩余格上每个滤子并不都是n重PMTL滤子,即n重PMTL滤子是非交换剩余格上的特殊滤子.
例 2.1设
L={0,a,b,c,d,1},
0 0abcd10000000a00a0aab00b0bbc0aacccd0abcdd10abcd1 →0abcd10111111ab11111b0c1c11cbbb111d0abc1110abcd1 0abcd10111111ac11111bcc1c11c0bb111d0abc1110abcd1 则L为非交换剩余格[15].容易验证F={1}是L上的滤子但不是2重PMTL滤子,因为 (b2→c)∨(c→b)=d∉F. 命题 2.1每个1重PMTL滤子都是n重PMTL滤子,但反之不一定成立. 证明由不等式 (x→y)∨(y→x)≤(xn→y)∨(y→x), 可知,显然成立. 0abcd10000000a00000ab00000bc00000cd0abcdd10abcd1 →0abcd10111111ac1c111bcc1111cccc111dcccc1110abcd1 0abcd10111111ad1d111bdd1111cddd111d0abc1110abcd1 则L是非交换剩余格[24].容易验证F={1}是n重PMTL滤子(n≥2),但不是PMTL滤子,因为 (a→b)∨(b→a)=c∉F. 命题 2.2每个n重PMTL滤子都是(n+1)重PMTL滤子,但反之不一定成立. 证明因为 xn→y≤xn+1→y 和 则有 (xn→y)∨(y→x)≤(xn+1→y)∨(y→x) 且 从而结论成立. 由数学归纳法可以得到下面的命题. 命题 2.3每个n重PMTL滤子都是(n+k)重PMTL滤子,但反之不一定成立,其中k∈N+. n重PMTL滤子具有如下扩张定理. 定理 2.1设F和E是非交换剩余格L的滤子且满足F⊆E.如果F是n重PMTL滤子,那么E是n重PMTL滤子. 证明因为F是L的n重PMTL滤子,所以 ∀x,y∈L, 有 (xn→y)∨(y→x)∈F, 且 又F⊆E,故 (xn→y)∨(y→x)∈E, 且 因此,E是n重PMTL滤子. 定理 3.1F是非交换剩余格L的滤子,则对于任意x,y,z∈L,以下条件等价: 1)F是n重PMTL滤子; 2)x→(yn∨z)∈F蕴含 (x→y)∨(x→z)∈F, 3) [x→(yn∨z)]→[(x→y)∨(x→z)]∈F, 证明1)⟹2) 设F是n重PMTL滤子,且 x→(yn∨z)∈F, 那么由引理1.1的9)、1)和11)、12)可以得到如下2个不等式链: [(yn→z)∨(z→y)]⊗[x→(yn∨z)]= {(yn→z)⊗[x→(yn∨z)]}∨ {(z→y)⊗[x→(yn∨z)]}= {[(yn∨z)→z]⊗[x→(yn∨z)]}∨ {[(y∨z)→y]⊗[x→(yn∨z)]}≤ {[(yn∨z)→z]⊗[x→(yn∨z)]}∨ {[(y∨z)→y]⊗[x→(y∨z)]}≤ (x→z)∨(x→y), 因此, 2)⟹3) 设u=x→(yn∨z),由引理1.1的8)可知 u→u=(u⊗x)→(yn∨z)∈F, 蕴含 [(u⊗x)→y]∨[(u⊗x)→z]∈F. 利用引理1.1的8) 和10)有不等式 [(u⊗x)→y]∨[(u⊗x)→z]= [u→(x→y)]∨[u→(x→z)]≤ u→[(x→y)∨(x→z)]. 因此, [x→(yn∨z)]→[(x→y)∨(x→z)]∈F. 蕴含 利用引理1.1的8)和10)有不等式 因此, 3)⟹1) 令x=yn∨z,则结论成立. 定理 3.2F是非交换剩余格L的滤子,则对于任意x,y,z∈L,以下条件等价: 1)F是n重PMTL滤子; 2) (y∧z)→x∈F蕴含 (yn→x)∨(z→x)∈F, 蕴含 证明1)⟹2) 设F是n重PMTL滤子,且 那么由引理1.1的9)、12)、2)和11)可以得到如下2个不等式链: [(y∧z)→x]⊗[(yn→z)∨(z→y)]= {[(y∧z)→x]⊗(yn→z)}∨ {[(y∧z)→x]⊗(z→y)}≤ {[(yn∧z)→x]⊗(yn→z)}∨ {[(y∧z)→x]⊗(z→y)}= {[(yn∧z)→x]⊗[yn→(yn∧z)]}∨ {[(y∧z)→x]⊗[z→(y∧z)]}≤ (yn→x)∨(z→x), 因此 (yn→x)∨(z→x)∈F, 2)⟹ 3) 设u=(y∧z)→x,由引理1.1的5)可知, 蕴含 利用引理1.1的5)和10) 有不等式 因此, 蕴含 利用引理1.1的5)和10) 有不等式 因此 3)⟹1) 令x=y∧z,则结论成立. 定理 3.3F是非交换剩余格L的滤子,则对于任意x,y,z∈L,以下条件等价: 1)F是n重PMTL滤子; 2)x→zn∈F蕴含 (x→y)∨(y→z)∈F, 蕴含 3) (x→zn)→[(x→y)∨(y→z)]∈F, 证明1)⟹2) 设F是n重PMTL滤子,且 那么由引理1.1的9)、11)和12),可以得到如下2个不等式链: [(zn→y)∨(y→z)]⊗(x→zn)= [(zn→y)⊗(x→zn)]∨ [(y→z)⊗(x→zn)]≤ [(zn→y)⊗(x→zn)]∨(y→z)≤ (x→y)∨(y→z), 因此 (x→y)∨(y→z)∈F, 2)⟹3) 设u=x→zn,由引理1.1的(8)可知, u→u=(u⊗x)→zn∈F 蕴含 [(u⊗x)→y]∨(y→z)∈F, 利用引理1.1的8)、4)和10)有不等式 [(u⊗x)→y]∨(y→z)= [u→(x→y)]∨(y→z)≤ [u→(x→y)]∨[u→(y→z)]≤ u→[(x→y)∨(y→z)]. 因此 (x→zn)→[(x→y)∨(y→z)]∈F; 蕴含 利用引理1.1的(8)(4) 和(10) 有不等式 因此, 3)⟹1)令x=zn,则结论成立. 定理 3.4F是非交换剩余格L的滤子,则对于任意x,y,z∈L,以下条件等价: 1)F是n重PMTL滤子; 证明1)⟹2) 设F是n重PMTL滤子,则由引理1.1的3)、1)、12)、7)和8)可得以下不等式: (xn→y)∨(y→x)≤ 从而 2)⟹3) 如果 那么由定理3.4的2)和引理1.2显然可得 3)⟹1) 令 z=(xn→y)∨(y→x), 则 从而 由定理3.4的3)得 又由引理1.1的10)和7)得 [(xn→y)∨(y→x)]≤(xn→y)∨(y→x), 故 (xn→y)∨(y→x)∈F. 同理,令 可得 从而F是n重PMTL滤子. 定义 4.1非交换剩余格L如果对任何 x,y∈L, 则称L为n重PMTL代数. 根据定理2.1的扩张性质,可以得到n重PMTL代数的如下特征定理. 定理 4.1设F是非交换剩余格L的滤子,则下列条件等价: 1) {1}是n重PMTL滤子; 2) 每个滤子是n重PMTL滤子; 3)L是n重PMTL代数. 证明1)⟹2) 由定理2.1显然成立. 2)⟹3) 因为每个滤子都是n重PMTL滤子,特别地,{1}是n重PMTL滤子.因此,对任何 x,y∈L, 有 (xn→y)∨(y→x)∈{1}, 且 即 从而L是n重PMTL代数. 3)⟹1) 显然成立. 定理 4.2设L是非交换剩余格,则以下各条件等价: 1)L是n重PMTL代数; 2)x≤(yn∨z)蕴含 4) (y∧z)≤x蕴含 6)x≤zn蕴含 证明由定理3.1~3.4和定理4.1的1)和3) 知,显然成立. 推论 4.1设L是非交换剩余格,则以下各条件等价: 1)L是伪MTL代数; 2)x≤(y∨z)蕴含 4) (y∧z)≤x蕴含 6)x≤z蕴含 素滤子是研究逻辑代数的一类重要滤子,学者们在不同的逻辑代数中提出并研究了素滤子的概念和性质,得到了一系列结果[25-32]. 在这些研究的基础上,Gasse等[33]提出,对于任何交换剩余格L,若素滤子和并素滤子一致,则L为MTL代数.随后,Kondo等[34]给出了确切的证明;文献[35]将结果推广到非交换剩余半格上,通过素滤子之集来刻画伪MTL代数.基于此,考虑提出n重素滤子的概念,并用n重素滤子的类来刻画n重PMTL代数. 定义 5.1设F是非交换剩余格L的滤子,如果x∨y∈F,那么x∈F或y∈F,则称F是L的并素滤子. 定义 5.2设F是非交换剩余格L的滤子.对 ∀x,y∈L, 若 xn→y∈F, 或 y→x∈F, 则称F为L的n重→素滤子; 若 或 定义 5.3设L为非交换剩余格.对 ∀x,y∈L, 若 (xn→y)∨(y→x)=1, 则称L为n重→ MTL 代数; 若 定理 5.1设L为非交换剩余格,则 1)L为n重→MTL代数,则 PF∨(L)⊆NPF→(L); 3)L为n重PMTL代数,则 PF∨(L)⊆NPF(L). 证明1)L为n重→MTL代数,设 F∈PF∨(L),x,y∈L. 因为 (xn→y)∨(y→x)=1∈F, 则 xn→y∈F, 或 y→x∈F, 故 F∈PF→(L), 从而 PF∨(L)⊆NPF→(L). 2) 证明过程与1)类似. 3)L为n重PMTL代数,则由1)和2)可得 下面例子表明L为n重PMTL代数,但 NPF(L)PF∨(L). 例 5.1如例2.2所示的非交换剩余格L,因为{1}是n重PMTL滤子,则由定理4.1可知L为n重PMTL代数.容易验证{1}是n重素滤子,但不是并素滤子,因为 c∨d=1∈{1}, 但 c∉{1},d∉{1}. 定理 5.2设L为非交换剩余格,则 1)L为n重→MTL代数当且仅当 PF∨(L)⊆NPF→(L); 3)L为n重PMTL代数当且仅当 PF∨(L)⊆NPF(L). 证明1) 定理5.1已证明了必要性. 充分性 假设 PF∨(L)⊆NPF→(L) 且L不是n重→ MTL 代数.因此,存在 a,b∈L, 使得 (an→b)∨(b→a)≠1. 令 G1=∩{G∈(L)|G≠{1}}. 首先,设G1={1},则由文献[35]中的定理5.5可知,存在一个并素滤子P,使得 (an→b)∨(b→a)∉P, 又因为P也是n重→素滤子,则 (an→b)∈P 或 (b→a)∈P, 即 (an→b)∨(b→a)∈P, 与上式矛盾,故假设不成立.其次,设 G1≠{1}, 则{1}是并素滤子也是n重→素滤子,则 (an→b)∈{1} 或 (b→a)∈{1}, 即 (an→b)∨(b→a)=1. 与假设矛盾.综上,L是n重→MTL代数. 2) 证明过程与(1)类似. 3) 定理5.1已证明了必要性. 充分性 因为 则由1)和2)易得L为n重PMTL代数. 本文在非交换剩余格上引入了n重PMTL滤子的概念,通过研究其特征和性质,获得了这类滤子的一系列等价条件,提出了n重PMTL代数的概念,得到了n重PMTL代数的若干特征定理,同时提出n重素滤子的定义,给出了n重PMTL代数的另一种刻画.相关结果丰富了非交换剩余格上的滤子理论.












3 n重PMTL滤子的刻画






















































































4 n重PMTL代数及其特征定理








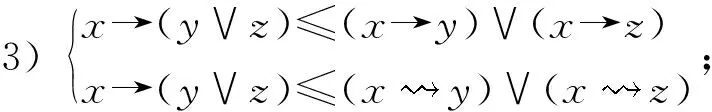

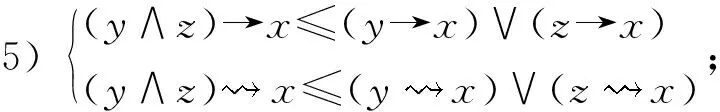

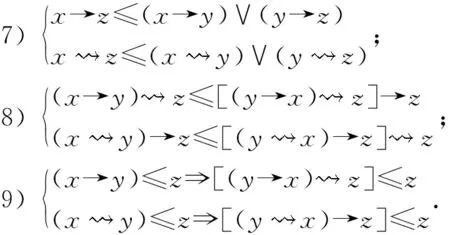
5 n重素滤子及n重PMTL代数的另一种刻画











6 总结

