图的圈和树孤立∗

张刚，吴宝音都仍

(新疆大学 数学与系统科学学院，新疆 乌鲁木齐 830017)

0 引言

除非特别说明,本文中G=(V,E)均表示一个顶点集为V=V(G),边集为E=E(G)的有限简单图.我们用n=|V|与m=|E|分别表示图G 的顶点数与边数.对任意的u,v ∈V(G),如果uv ∈E(G),那么我们称u 在图G中是v 的一个邻点,反之亦然.对任一v ∈V(G),v 的开邻域定义为集合NG(v)=N(v)={u ∈V(G)|uv ∈E(G)},v 的闭邻域定义为集合NG[v]=N[v]=N(v)∪{v}.另外,dG(v)=d(v)=|N(v)| 表示顶点v 在图G 中的度数.通常,Δ(G)和δ(G)被称为图G的最大度和最小度.设S 是G 的一个顶点子集,则S的开邻域记为NG(S)=N(S)=∪v∈SN(v)S,S的闭邻域记为NG[S]=N[S]=N(S)∪S.我们用G[S]表示图G中由S导出的子图,用G-S 表示图G 中V S 的导出子图.对于其他未定义的术语和概念，读者们可参阅文献[1].

设F 是一个连通图集,对任一图G,如果顶点子集D 使得G-N[D]不包含任一F 中的F 图作为子图,那么D 被叫做图G 的一个F 孤立集,且图G 中最小的一个F 孤立集D 的阶数被称为图G 的F 孤立数,记为ι(G,F).另外,一个顶点子集D 被称为图G 的一个控制集,如果V(G)D 中的每个顶点在D 中都至少有一个邻点.图G 中最小的一个控制集D 的阶数即是图G 的控制数,记为γ(G).显然,ι(G,{K1})=γ(G).

图的孤立, 亦被称为部分控制, 它是经典控制理论的一种自然推广. 2017 年, Caro 和Hansberg[2]首次引入了这些概念. 对于该领域进一步的研究, 可参阅文献[3-7]. 除此之外, 对于一些经典控制问题, 读者们可参阅文献[8-14].

1 主要结果

本文得到的主要结论如下,其详细的证明将被放在第2 小节进行.

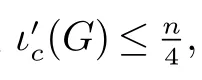
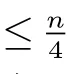
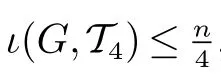
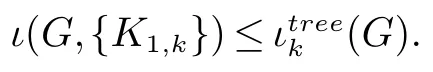
受此启发,对任意的正整数k,我们希望考虑F={Pk}的情形.由此,提出问题:计算n 个顶点的连通图G 中ι(G,{Pk}) 的准确上界.显然,因为图G 的一个Ck∪Tk+1孤立集一定是图G 的一个{Pk+1} 孤立集,有ι(G,{Pk+1})≤ιtreek(G).

推论4如果G/=C7是一个n 个顶点的连通图,那么ι(G,{P4})≤n

4,且这个上界是紧的.

定义girth(G)表示图G 的围长,即是图G 中最短的一个导出圈的长度.我们提出下列猜想,其实际上是定理1 的一个推广.

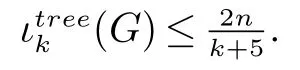
2 证明

在这一节,我们将会证明本文的主要定理.下面首先给出几个引理.其中,引理1、引理2、引理3易证,我们将其证明留给读者.

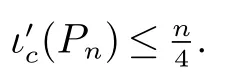
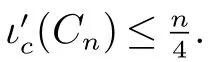
引理4假设F 是一个连通图集,G=(V,E)是一个有限简单图.对于任意一个顶点子集S,如果G[S]中有一个F 孤立集D,且使得E(SN[D],V S)=∅,那么ι(G,F)≤|D|+ι(G-S,F).

证明设D′是G-S 的一个F 孤立集,且|D′|=ι(G-S,F).我们仅需证明D ∪D′是G 的一个F 孤立集即可.反证如下,假设G-N[D ∪D′] 中存在一个F 中的F 图作为其子图.根据D 和D′的选择,我们有V(F)⊆(SN[D])∪((V S)N[D′]),V(F)∩(SN[D])/=∅和V(F)∩((V S)N[D′])/=∅.然而,这是不可能的,因为F 是连通的且E(SN[D],V S)=∅.

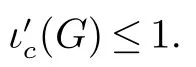
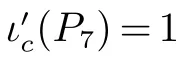
令V(G)={v1,v2,···,v7},设N(v1)={v2,v3,v4},V(G)N[v1]={v5,v6,v7}.如果|E(G-N[v])|≤2,则取D={v1},于是(G) ≤|D|=1.所以G-N[v1]～=C3.因为G 是连通的,根据其对称性,此时我们不妨假设v2v5∈E(G),显然N(v5)={v2,v6,v7}.注意到如果v3v4/∈E(G),则取D={v5},而此时(G)≤|D|=1.因此我们假设v3v4∈E(G).如果此时dG(v2)=3,那么G-N[v2]/=C3,所以我们可以取D={v2},同时有(G)≤|D|=1.显然{v1,v5}⊆N(v2),所以dG(v2)=2.如果{v3,v4,v6,v7}中存在一个顶点x 使得dG(x)=3,那么dG-N[x](v2)=1,所以可取D={x},进而有(G)≤|D|=1.因此,对于每个x ∈{v3,v4,v6,v7},dG(x)=2,那么当前可取D={v2},也有(G)≤|D|=1.

为了方便起见,如果图G 的一个连通分支同构于C3或者C7,那么我们称之为坏分支,反之我们称之为好分支.

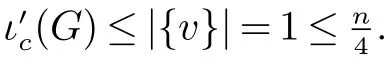
如果Hb=∅,显然{v}是G[N[v]]的一个{C3,K1,3,P4}孤立集,根据引理3 和引理4,我们有

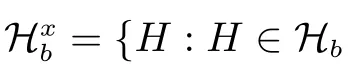
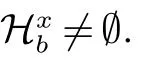
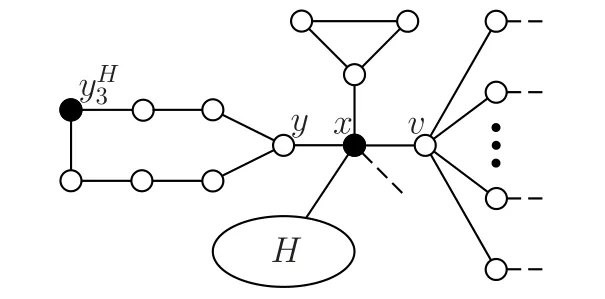
图1 存在某个x ∈N(v)使得Hxb/=∅

子情况1.1(G-X)v/∈{C3,C7}.

根据归纳假设,再结合引理3 和引理4,我们有

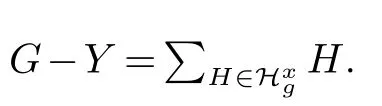
子情况1.2(G-X)v～=C3.

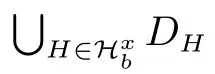
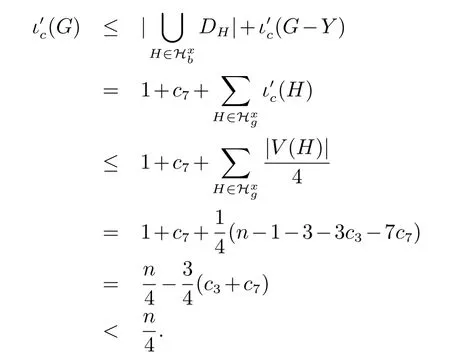
子情况1.3(G-X)v～=C7.

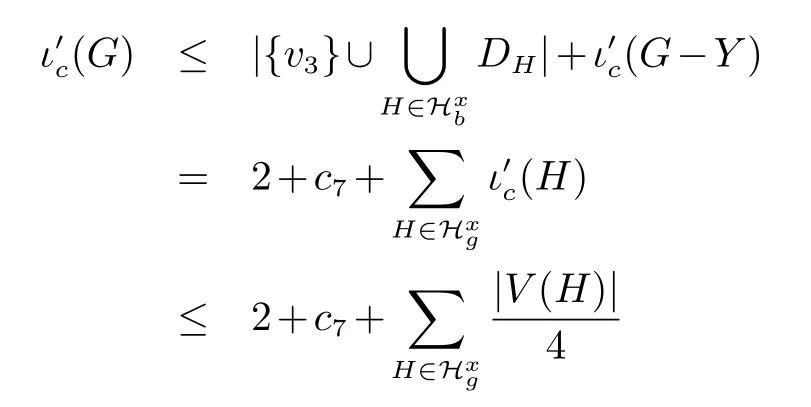
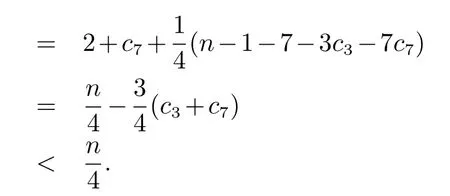
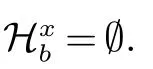
根据当前的假设,等价的,对于任意一个H ∈Hb,有|N(H)∩N(v)|≥2.下面的证明,我们将分为两种子情况来讨论.

子情况2.1存在一个H ∈Hb,H～=C3.

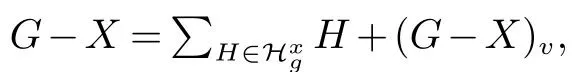
子情况2.1.1(G-X)v/∈{C3,C7}.

根据归纳假设,再结合引理3 和引理4,我们有

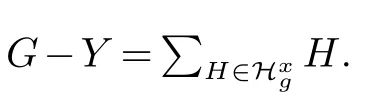
子情况2.1.2(G-X)v～=C3.

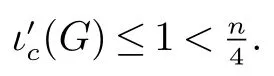
图2 H′～=C3～=(G-X)v

子情况2.1.3(G-X)v～=C7.

结合当前假设,我们也可得到Δ(G)=dG(v)=3,如图3 所示.因为|N(H′)∩N(v)|≥2,所以存在x′使得x′∈(N(H′)∩N(v)){x}.注意到{v,x′}是G[Y]的一个{C3,K1,3,P4}孤立集,因此根据引理3 和引理4,以及归纳假设,我们有

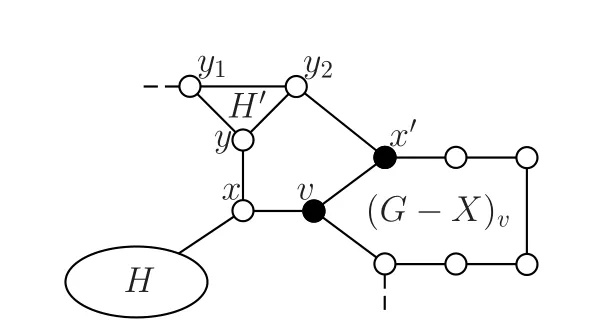
图3 H′～=C3，但(G-X)v～=C7

子情况2.2任意一个H ∈Hb,H～=C7.

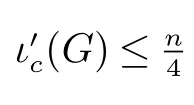
子情况2.2.1存在两个H1,H2∈Hb使得某个x′∈N(H1)∩N(H2)∩N(v).

图4 存在一个x′∈N(v)使得x′∈N(H1)∩N(H2)

子情况2.2.2任意两个H1,H2∈Hb,N(H1)∩N(H2)∩N(v)=∅.

因为对于每个H ∈Hb,|N(H)∩N(v)|≥2,所以当前的条件暗示着Δ ≥2b.再结合Δ-2 ≤b,我们有Δ ≤4和b ≤2.因此,Δ ∈{3,4},b ∈{1,2}.于是,现在我们仅需再考虑Δ 和b 两两组合可能出现的四种子情况即可.然而,当Δ=3 且b=2 时,如图5 所示,我们已在子情况2.2.1 进行了讨论.当Δ=4 且b=1 时,如图6 所示,该子情况已经与Δ-2 ≤b 矛盾.

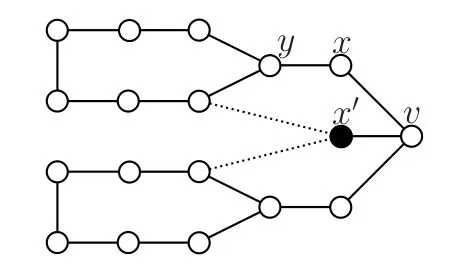
图5 Δ=3 且b=2

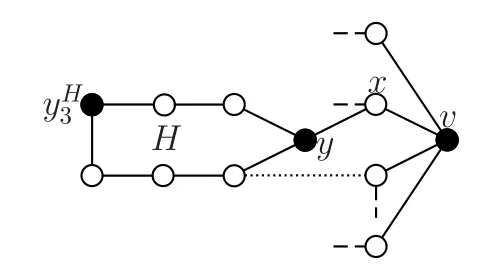
图6 Δ=4 且b=1

最后我们来讨论Δ=3 且b=1和Δ=4 且b=2 两种子情况.如果Δ=3 且b=1,如图7 所示,那么我们假设Hb={H′},xy,x′y′∈E(G),其中x,x′∈N(v),y,y′∈V(H′),且x/=x′,y/=y′.令X={x,x′}∪V(H′).因为dG-X(v)=dG(v)-2=Δ-2=3-2=1,所以G-X 中一定没有坏分支.显然,此时{y,y′} 是G[X]的一个{C3,K1,3,P4}孤立集.根据归纳假设,再结合引理3 和引理4,我们有

图7 Δ=3 且b=1

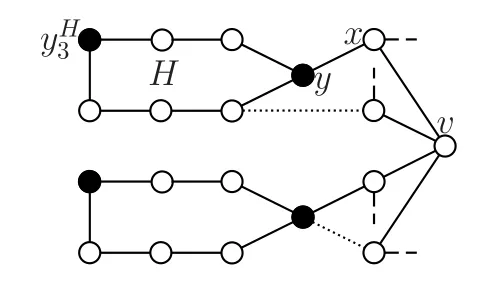
图8 Δ=4 且b=2

到此完成定理1 的证明.