新疆杨木柱偏心受压试验研究∗

李亮翔，刘 清，韩 霞，谭鑫宇，殷 芳

(新疆大学 建筑工程学院，新疆 乌鲁木齐 830017)

0 引言

新疆杨属于落叶乔木类，广泛分布在新疆地区[1]，具有耐干旱、耐盐渍、喜光、速生等特性，新疆杨材质较好，树干纹理顺直，是一种绿色生态、低碳环保的可再生资源[2-5].同时，我国现行《木结构设计标准》（GB 50005―2017）[6]尚未明确给出新疆杨材料基本力学性能指标和强度等级的划分标准，这限制了新疆杨在木结构建筑中的推广应用.

目前国内外学者对木柱开展了许多研究，并取得了一定的研究成果.国外学者Plevris[7]、Husam[8]等对木柱进行了试验研究，国内学者朱雷[9]、许清风[10]、李向民[11]、周钟宏[12]、周长东[13]等分别对花旗松、杉木等进行了轴压力学性能研究.欧阳煜[14-15]等以樟子松为基材，对60 mm×60 mm×850 mm长木柱进行偏心受压试验，结果表明：偏心荷载作用下长木柱的横向应变不明显，其受压极限承载力为53.34 kN，延性系数为1.35.然而，国内外学者针对新疆杨木柱研究较少，王静辉[16]等研究偏心距分别为0 mm、50 mm和100 mm的新疆杨木方形截面长柱的偏心受压力学性能，结果表明：长柱以典型的中部弯曲破坏形式为主，偏心距对其受压承载力影响更为显著.文献[16]设计偏心距的增大值较大，未能充分考虑偏心距增大值较小时对新疆杨木柱偏心受压力学性能的影响.

综上所述，针对松木、杉木等少数树种的木柱进行轴心受压力学性能研究较多，同时，在实际土木工程中偏心受压木柱比较常见，对新疆杨木柱偏心受压力学性能的研究相对较少，尤其是当偏心距增量值较小时，对新疆杨木柱的偏心受压力学性能等的影响研究更少.因此，本文以新疆杨为原材料，针对木柱长细比为48，偏心距分别为0 mm、30 mm、45 mm、60 mm的新疆杨木柱，制作12根试件，主要研究不同偏心距对试件的破坏形态及偏心受压力学性能的影响，从而为新疆杨木在土木工程中的推广应用提供试验及理论依据.

1 试验概况

1.1 试验原材料

本试验材料取自新疆和田林场的新疆杨，所有试件均取同一批次原木，新疆杨基本物理力学性能指标如表1所示.

表1 新疆杨基本物理力学性能

1.2 木柱设计与制作

根据《木结构试验方法标准》（GB/T 50329―2012）[17]设计4组试件尺寸为100 mm×100 mm×1 300 mm的偏心受压木柱（图1），每组3根，共12根，参数见表2.

图1 木柱尺寸图（mm）

表2 新疆杨木柱设计参数

1.3 试验及量测方案

1.3.1 试验装置

本试验采用WEY5000微机控制电液伺服压力试验机，使用DH3816静态应变测试仪同步采集试验数据，支座上下均采用单向刀铰支座，为了保证试验准确性，试验前应在试件两端标记偏心距位置并且通过单向刀铰装置上两侧螺杆的伸缩来实现偏心距.试验加载装置如图2所示.

图2 试验装置

1.3.2 试验加载

根据《木结构试验方法标准》（GB/T 50329―2012）[17]规定，试验采用位移加载方式，加载速度为2 mm/min的连续均匀加载，当施加荷载下降至试件极限荷载的85%或试件发生明显破坏时，停止试验.

1.3.3 试验量测

如图3（a）所示，轴心受压木柱A、B、C侧面中部分别布置1个竖向应变片，D侧面中部布置1个横向应变片，用于测量各个侧面的应变及确定木材的泊松比，同时在A侧面高度的1/2、3/4处和C侧面高度的1/4、1/2处分别安装位移计，用于测量轴心受压木柱的侧向挠度.

如图3（b）所示，偏心受压木柱受拉侧高度的四分点处和受压侧高度的1/2处分别安装位移计，以测量侧向挠度.在木柱受压侧A面和受拉侧G面中部分别布置1个竖向应变片，H面中部布置1个横向应变片.在B面中部宽度处等间距布置5个竖向应变片，用来验证平截面基本假定.

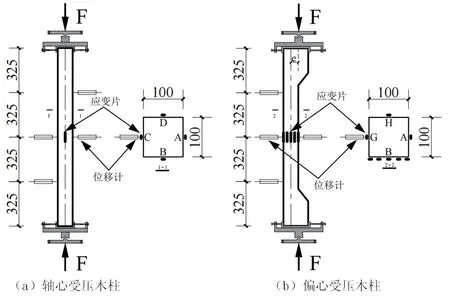
图3 应变片及位移计布置图（mm）

2 试验结果及分析

2.1 主要试验结果

本试验的主要结果见表3，其中：Δ0、Δu分别为峰值荷载所对应的竖向位移、荷载下降到峰值荷载85%时所对应的竖向位移；ωm为峰值荷载所对应的柱中部的侧向挠度；Mu为试件极限弯矩值.

表3 试验结果

2.2 试验破坏现象

如图4（a）所示，对于偏心距为0 mm的PXJ1试件，加载初期试件中部无明显挠度.当荷载达到176 kN时，柱身侧向挠度出现明显增加的迹象，试件中部受压侧边缘首先出现横向细微裂缝并伴随着轻微开裂声；当荷载达到峰值220.28 kN时，试件出现明显的挠度，受压侧中部发生明显褶皱.同时，横向裂缝向受拉侧延伸，并伴随着连续“噼啪”声，最终试件因受压侧发生局部褶皱同时受拉侧边缘木纤维被拉断，整个破坏主要表现压弯破坏现象.

如图4（b）所示，对于偏心距为30 mm的PXJ2试件，当荷载达到约80 kN时，试件发出连续轻微响声，侧向挠度增长较明显，加载至峰值100.57 kN时，发出巨大开裂声并且试件中部受拉侧边缘出现细小斜裂缝，随后，受拉侧裂缝缓慢向上发展，最终以受拉侧边缘木纤维被拉断而导致试件破坏，断口表现为锯齿形.

如图4（c）所示，对于偏心距为45 mm的PXJ3试件，当荷载达到约41 kN时，木柱发出连续的劈裂声；荷载加载至峰值82.52 kN时，发出巨响“噼啪”声并伴随着受拉侧中部边缘出现纵向裂缝；随后，受拉侧裂缝缓慢向下发展，最终试件破坏时裂缝延伸长度约为200 mm，对应的主裂缝宽度约为10 mm.

如图4（d）所示，对于偏心距为60 mm的PXJ4试件，当荷载达到约32 kN时，木柱发出连续的劈裂声，加载至峰值63.94 kN时，发出巨响劈裂声并且试件中部受拉侧及正面边缘处出现斜裂缝.随后，受拉侧裂缝缓慢斜向上延伸，最终以受拉侧中部偏上225 mm处木纤维被拉断而导致试件破坏.

图4 轴压和偏压木柱典型的破坏形态

综上所述，虽然PXJ1～PXJ4试件的破坏形态均表现为压弯破坏，但是破坏过程有所区别.其中：PXJ1试件中部受压侧首先出现局部褶皱破坏，然后受拉侧边缘木纤维被拉断，受压侧先于受拉侧发生破坏；而偏心受压PXJ2～PXJ4试件中部受拉侧边缘木纤维先发生拉断，受压侧表现出不同程度的褶皱，受拉侧先于受压侧发生破坏.

2.3 荷载-位移曲线分析

图5（a）为不同偏心距下新疆杨木柱的荷载-竖向位移曲线.试件的荷载-竖向位移曲线的整体变化趋势为：在加载初期，竖向位移随着荷载增加呈线性增加，其中偏心距为0 mm的试件荷载增长速度最快；随着荷载继续增大，荷载-竖向位移曲线斜率逐渐减小，曲线趋于平缓并最终达到峰值点，之后曲线逐渐下降.对比不同偏心距工况下的试件，极限荷载对应的竖向位移随着偏心距的增大而增大，其极限荷载值为220.28 kN、100.57 kN、82.52 kN和63.94 kN时对应的竖向位移分别为12.83 mm、15.00 mm、18.21 mm和19.18 mm.此外，随着偏心距的增大，试件极限荷载显著减小，曲线下降段逐渐趋于平缓.定义竖向位移延性系数µ=Δu/Δ0，式中Δ0、Δu分别为峰值荷载所对应的竖向位移、荷载下降到峰值荷载85%时所对应的竖向位移.偏心受压试件PXJ2～PXJ4的延性系数分别为1.54、1.38和1.36，随着偏心距的增大，试件的竖向位移延性系数减小.这表明虽然极限荷载对应的竖向位移随着偏心距的增大而增大，但是试件达到峰值后的延性有所降低.

图5（b）为不同偏心距下试件的荷载-侧向挠度曲线.其中偏心距为0 mm的轴心受压试件（PXJ1），在加载初期，荷载与侧向挠度呈线性关系，且斜率较大，表现出木柱较强的承载能力；当加载达到极限荷载时，木柱试件开始出现明显挠度，之后曲线平缓呈现出荷载基本不变而侧向挠度仍然继续增大的趋势；当试件的侧向挠度约达到13 mm后，木柱承载能力下降速度很快，并最终发生压弯破坏.偏心受压试件（PXJ2～PXJ4）的荷载-侧向挠度曲线反映了在偏心加载过程中试件的侧向变形状况.各试件的荷载-侧向挠度曲线与相应的荷载-竖向位移曲线形状相近，相同竖向荷载作用下，偏心距越大的试件其侧向挠度越大，说明对于偏心受压的新疆杨木柱其受压偏心距越大，侧向弯曲变形越显著.

图5 新疆杨木柱荷载-位移曲线

2.4 荷载-纵向应变关系

由图6（a）可知，轴心受压试件PXJ1在试验加载初期，全截面承受压应力，A面和C面的纵向应变都表现为压应变，试件A面的压应变发展速率比C面的快，且随着加载线性增加.当试件荷载接近极限荷载时，C面的压应变增速放缓，达到极限荷载后，压应变出现减小趋势，进而转变为拉应变，主要受木材的天然缺陷及不均匀性等因素影响，试件受压时必然会产生附加弯矩，由附加弯矩引起的拉应变与轴向压力引起的压应变共同作用造成的.当试件荷载达到极限荷载时，新疆杨木柱A面压应变约为6 500×10-6，最终试件破坏时，A面发生局部褶皱，C面边缘木纤维被拉断，木柱的破坏主要表现出整体压弯破坏现象.

由图6（b）可知，对于偏心受压试件（PXJ2～PXJ4）从开始加载至最终破坏，试件表现出中部A面受压以及G面受拉的应变反应，规律较明显，偏心荷载产生的弯曲效应显著，并且A面和G面荷载-纵向应变关系曲线基本对称，荷载达到极限荷载时偏心受压试件的受压侧所对应的压应变值约为（5 850～7 680）×10-6，试件的受拉侧拉应变约为（2 850～6 000）×10-6，各偏心受压试件都表现为受拉侧先于受压侧破坏.同时，根据图6（a）和图6（b）对比，得出偏心受压试件的受压侧压应变值略大于轴心受压试件，从受压侧的应变变化规律可以看出，新疆杨木柱的偏心受压试件的受压变形能力及强度得到了充分的发挥.

图6 典型新疆杨木柱荷载-纵向应变曲线

图7为整体加载过程中偏心距为30 mm、45 mm、60 mm的各个试件中部截面的纵向应变沿截面高度的分布情况.所有试件横截面应变沿高度方向呈线性关系，但中和轴的位置存在差异，偏心距为30 mm和45 mm的试件截面的中和轴分别向受拉侧移动了约15 mm和10 mm，而偏心距为60 mm的试件，中和轴位置向受压侧移动了约4 mm.说明随着偏心距的增加，中和轴从受拉侧向受压侧移动的趋势，基本上满足平截面假定.

图7 应变沿截面高度的分布

2.5 极限承载力分析

如图8所示，当偏心距从0 mm变化到30 mm时，试件的极限承载力从220.28 kN下降至100.57 kN，下降幅度为54%，承载力降低幅度较大；当偏心距从30 mm变化到45 mm、60 mm时，随着偏心距的增大，极限承载力分别从100.57 kN下降至82.52 kN、63.94 kN，下降幅度分别为17.9%、22.5%，承载力降低幅度相对较小.这说明随着偏心距的增大，极限承载力降低幅度呈现出减小趋势.同时，由图8可以看出：当偏心距从0 mm变化到60 mm时，试件的极限承载力从220.28 kN下降至63.94 kN，下降幅度为71%.整体上新疆杨木柱极限承载力随着偏心距的增大呈现减小的趋势，虽然偏心距增量较小时承载力降低幅度较小，但是偏心距从0 mm增加到60 mm时，承载力的降低幅度最大，因此，偏心距对木柱的偏心受压极限承载力影响显著.其主要原因是试件在偏心压力作用下，随着偏心距的增大，侧向挠度逐渐增大，并且侧向挠度产生附加弯矩，最后，试件在破坏截面处的初始弯矩和附加弯矩同时作用下，其极限承载力急剧降低.

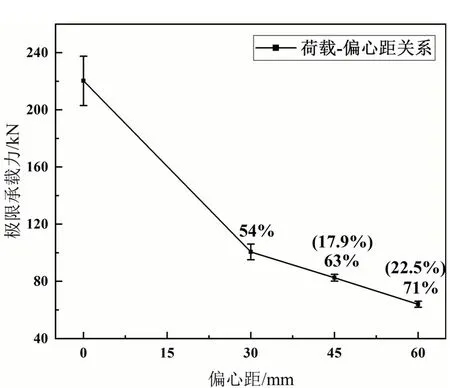
图8 偏心距对木柱极限承载力的影响

2.6 偏心受压承载力计算

图9给出了在极限偏压荷载作用下，典型新疆杨木柱1/2高度处截面弯矩-轴力相关关系.由图9可知，随着偏心距的增大，试件的轴向压力呈现减小的趋势，而弯矩值表现为增大的变化规律，随着偏心距从0 mm变化到45 mm，弯矩值增大幅度较大，但偏心距从45 mm变化到60 mm，弯矩值基本不变.

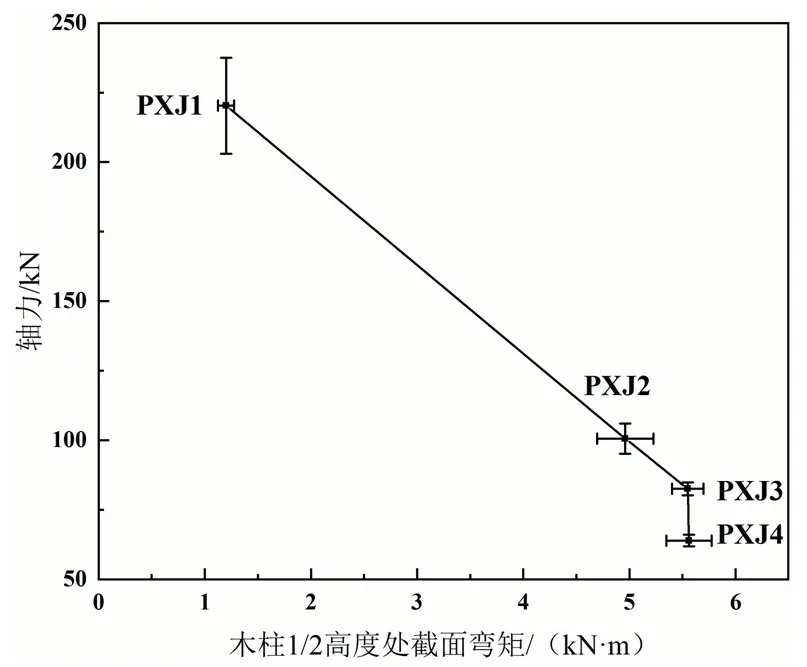
图9 新疆杨木柱弯矩-轴力关系曲线

图10给出了新疆杨木柱相对偏心率与轴力比的关系曲线.由图10可知，随着相对偏心率的增大，轴力比呈现减小的趋势，相对偏心率与轴力比的关系近似反比例函数.基于相对偏心率折减系数的新疆杨木柱承载力计算公式为：

图10 新疆杨木柱相对偏心率与轴力比的关系

式中：Nu为新疆杨木柱的偏心受压极限承载力；β为相对偏心率折减系数；N0为轴心受压木柱的极限承载力.参考《木结构试验方法标准》（GB/T 50329―2012）[17]计算试件的相对偏心率m，其计算公式为：

式中：e为偏心距，取荷载与试件轴线之间的距离（mm）；h为试件的截面高度（mm）.

根据试验结果计算相对偏心率折减系数β为：

结合公式（1）和公式（2）计算出的新疆杨木柱的偏心受压承载力结果见表4.由表4可知，试验均值与极限承载力计算值相对误差小于10%，因此，上述公式计算偏心受压柱的受压极限承载力与试验值吻合较好.

表4 试验结果与计算结果对比

3 结论

（1）所有试件的破坏形态均表现为压弯破坏，但破坏过程有所区别.其中：轴心受压试件中部受压侧首先出现局部褶皱破坏，然后受拉侧边缘木纤维被拉断，受压侧先于受拉侧发生破坏；而偏心受压试件中部受拉侧边缘木纤维先发生拉断，受压侧表现出不同程度的褶皱，受拉侧先于受压侧发生破坏.

（2）不同偏心距工况下的新疆杨木柱，随着偏心距的增大，荷载-竖向位移曲线峰值点对应的竖向位移增大，但竖向位移延性系数不断减小；荷载-侧向挠度曲线峰值点对应的侧向挠度随着偏心距的增大而增大，试件的侧向弯曲变形更显著.

（3）通过荷载-纵向应变分析，发现随着偏心距的增大峰值点对应的受压侧压应变不断增大，偏心受压试件的受压侧木材的受压变形能力及强度得到充分发挥；在不同偏压荷载作用下，木柱中部横截面应变沿截面高度的变化规律基本满足平截面假定.

（4）随着偏心距的增大，新疆杨木柱极限承载力呈现减小的趋势；相对偏心率与轴力比的关系近似反比例函数.基于此，本文提出了与偏心距相关的新疆杨木柱偏心受压承载力计算公式，相对误差小于10%，计算结果与试验结果吻合较好.