彰显知识的成与用：培养学生数学抽象素养的教学

邓皓月 仲秀英

[摘  要] 数学抽象是在具体情境中从数量关系与空间形式的角度抽象出数学对象.数学抽象的结果反映出不同水平的数学抽象素养. 彰显数学知识的形成与应用全过程，有助于培养学生的数学抽象素养.

[关键词] 数学抽象;数学应用;数学抽象素养

数学抽象素养在人的数学学习、理性思考、智力发展、科学探究和实践应用中具有重要的作用，培养学生的数学抽象素养是基础教育数学教学的重要任务. 了解数学抽象的基本过程，明晰数学抽象的结果与数学抽象素养的水平，能为培养学生数学抽象素养的教学提供参考依据.

数学抽象的基本过程

数学是研究现实世界空间形式和数量关系的学科，数学知识是由表达空间形式和数量关系及其特点的数学概念、公式、法则、性质与思想方法组成的.哲学家康德认为人类的一切知识都从直观开始[1]，数学知识的形成亦如此，始于直观，成于抽象. 通过观察直观事物或现象，发现其规律、特点、属性，得到符号化、形式化对象，建构出数学概念、公式、法则等数学知识，这是一种“直观化”的数学抽象. 例如，毕达哥拉斯在参加宴会时，偶然发现地砖之间的数量关系，从而得到所有的直角三角形斜边的平方都等于两直角边平方之和，形成勾股定理，这就是建立在直观经验基础之上的抽象，可以称之为“直观化”抽象.通过对已经抽象出的数学符号、公式与法则等进行拓展与延伸得到更形式化的对象，是一种“形式化”抽象. 例如，将勾股定理进一步延伸可以得勾股数组及其性质、不定方程x2+y2=z2，xn+yn=zn等数学模型，这是建立在对对象表达形式化、符号化基础之上的抽象.两种形态的数学抽象的基本过程都包括了感知对象、探索发现、概括共性与形成数学模型等四个基本环节.数学抽象是形成理性思维的重要基础，直观化抽象基于经验直观，形式化抽象基于一定的逻辑推理，但两者都是从形和量及其关系的角度抽取研究对象的本质属性以建构数学知识的过程，数学知识是数学抽象的结果，反映了数学的本质特征.

数学抽象的基本结果

通过对研究对象的形和量及其关系的抽象，其结果在数学上主要表现为数学概念、数学命题、数学思想方法、问题解决模型等基本形式.

数学概念是对事物或现象的规律、性质和特点的高度概括，具有高度抽象性、逻辑性与系统性[2]. 它的产生和形成有两种基本途径：其一是基于对现实事物或者现象的观察、分析，概括出本质属性，形成概念;其二是对已有的概念进一步限制或者拓展，得到新概念. 形成数学概念一般包括感知情境、发现共性、概括本质属性、给概念下定义等四个基本环节.

与数学概念类似，数学命题也是数学抽象的结果. 数学命题是数学定理、公式、法则的统称. 数学命题的形成也表现为两种基本途径：一是在具体情境中，通过对问题的探索与发现，抽象出关于某个研究对象的性质或判断，形成命题;二是在已有命题基础之上，对这些命题进行分析和演绎，提出一个新的命题.形成数学命题的过程可以概括为问题情境、提出猜想、验证猜想、形成命题等四个基本环节.

在运用数学概念和数学命题的过程中，蕴含了丰富的数学思想方法，形成了诸多的数学模型，例如数学中的化归思想、转化思想、方程思想、函数思想以及具体的问题解决模型等. 这些方法、思想和数学模型反过来又在数学抽象的过程中发挥着作用，影响着人们的思维与决断.

数学抽象素养的水平

数学抽象的类型不同，抽象的结果也不尽相同.不同的结果反映出不同水平的数学抽象素养. 例如，从运动变化的观点出发，在直观的情境中抽象出函数概念：“在一个变化过程中，有两个变量x和y，如果对于x的每一个确定的值，y都有唯一确定的值与其对应，那么就称y是x的函数.”这是用变量的观点定义函数，反映出借助直观情境建构数学知识的数学抽象素养.从集合与映射的观点出发，运用对应的观点定义函数：“设A，B是两个非空集合，按照确定的对应关系f，如果对于集合A中任意一个x，在集合B中都有唯一确定的数f（x）和它对应，则称f是从集合A到B集合的函数”，这是在多个概念之间建构出内在的数学关系，能反映出相关概念之间的逻辑联系，是一种形式化抽象.显然，后者的抽象程度更高，所體现的数学抽象素养也更高.数学抽象程度的高低，反映出数学抽象素养的高低.

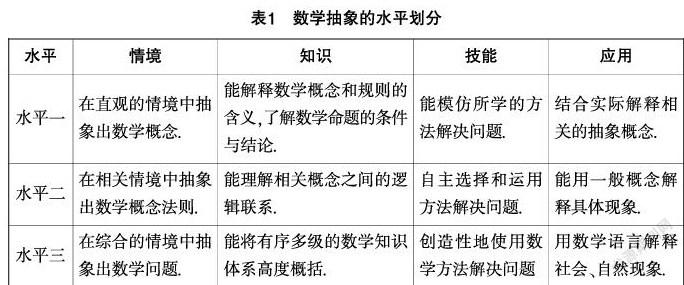
《普通高中数学课程标准（2017年版2020年修订）》[3]中对数学抽象素养从情境、知识、技能和应用”四个方面进行了水平划分（见表1），成为目前我国数学教育工作者评判学生数学抽象素养发展的重要依据.

培养数学抽象素养的教学举措

数学抽象素养是指在具体情境中能够从数量关系与空间形式的角度抽象出数学对象，并能应用数学知识与数学技能进行解释与应用的关键能力.

表1中数学抽象素养呈现出的不同水平表明，数学抽象素养是在不同情境中抽象、解释与应用数学知识和数学技能时加以体现并逐步养成的. 数学抽象素养的养成依托于情境，是一个不断经历抽象、反省抽象的过程，是个体在数学建构、数学理解、数学应用、数学思维、数学发现的过程中反复修炼、自主生成数学经验，形成数学知识的过程，也是对数学知识不断积累、自我反省、反复练习的过程[4]. 因此，彰显数学知识的形成与应用全过程，遵循数学抽象产生与应用的内在机制，按照感知情境、数学探究、适度形式化、数学应用的环节进行教学，让学生经历数学知识发生、形成与应用的全过程，有助于培养学生的数学抽象素养.

1. 感知情境：创设适于数学抽象的环境

数学知识是数学研究者在特定的环境下数学抽象的结果，其存在的形式往往已经剥离了原有的具体情境而显现出符号化、形式化的特征. 如果直接呈现这些知识，学生不仅难以理解与接受，也缺失了抽象素养养成的环境基础. 创设一个有利于学生进行数学抽象和运用数学抽象的情境，是培养学生数学抽象素养的基本前提.

从数学知识的形成过程可以发现，数学抽象的情境主要有现实情境、数学情境、文化情境三种基本类型. 能够促进学生进行数学抽象的现实情境往往是学生熟悉的、感兴趣的、有意义的生活情境. 例如在初中黄金分割教学中，可以学生熟悉的断臂维纳斯图片为例，固定维纳斯的身高，创设一个通过几何画板不断改变维纳斯上半身长与下半身长变化的情境，让学生在感知情境的变化中抽象出“比”“黄金分割比”“黄金分割数”等概念. 教师教学中，假定肚脐点以上为上半身，肚脐点以下为下半身，运用几何画板，上下拖动维纳斯的肚脐点，维纳斯的上半身与下半身的长度随着点的拖动不断变化. 学生在这样动态的情境中感受维纳斯美感的变化，认识到维纳斯从美到不美的原因是上下身长的“比”值在变化，抽象出从“比”的角度去刻画维纳斯美的变化，进而认识到当比值在某一固定值时，维纳斯才具有美感，从而抽象出黄金分割比和黄金分割数的概念. 当学生知道黄金分割数之后，又可以创设具有现实意义的情境让学生进行解释与应用，例如创设在一栋30层楼高的大厦买一套理想楼层的房子，应该选择多少层的问题情境，或者创设在某景点的一座塔上修建一个观光台，请学生建议如何确定观光台位置的情境，引导学生将情境中的问题抽象为求线段的黄金分割点的问题. 学生主动探究并对新学概念加以解释与应用的过程，有助于数学抽象素养的培养.

能够促进学生数学抽象的数学情境往往是学生在学过的数学知识的基础上发现新问题的情境. 这种情境可以是对原有的现实情境进行变式，也可以是纯粹从数学知识内部提出问题的情境. 例如，教学“圆”的定义可以创设的现实情境是在一个平面上，固定一根细绳的一个端点，拉直这根细绳，探究另一个端点在这个平面上绕着前一个端点旋转一周形成的图形. 将此情境进行变式：在一个平面上有一根细绳，固定这根细绳的两个端点，用一支铅笔在这个细绳中间的任一点拉直这根细绳并旋转一周，探究该点形成的轨迹，这就创设了探究椭圆定义的数学问题情境.学生在探究过程中逐渐抽象出“平面上，一个动点，两个定点，动点的轨迹，动点到两个定点距离和为定值，动点到两个定点距离和与两个定点之间的距离之间的关系”等数学属性，从而抽象出椭圆的概念. 当然，也可以直接类比圆的定义创设数学问题情境，在圆锥曲线教学伊始，教师可以提问：如果平面上到一定点的距离为定值的点的轨迹是圆，那么平面上到两个定点距离的和、差、积、商为定值的点的轨迹分别是什么？这样就创设了探究椭圆、双曲线以及其他图形的数学问题情境，学生可以在这样的问题情境中直接抽象出变化的量和不变的量及其之间的关系，建构新的数学概念.

数学知识在形成的过程中不乏很多具有教育意义的数学史料和数学故事. 能够促进学生进行数学抽象的文化情境主要是指将具有启发意义的数学史、数学故事作为情境，以及以与其他学科相联系为特征的情境，例如通过讲解毕达哥拉斯学派与第一次数学危机产生的背景，创设出“无理数”概念教学的情境;引入李白诗句“孤帆远影碧空尽，唯见长江天际流”，创设出“极限”概念教学的情境;引入古语“一尺之棰，日取其半，万世不竭”，创设出“无穷小”概念教学的情境等等. 这种蕴含了数学关系能够引起学生情感共鸣的文化情境，有助于激发学生用数学的语言去表达情境，用数学的知识和技能去思考与探究情境.

2. 数学探究：经历知识形成与抽象的全过程

好的情境能够有效激发学生的好奇心和求知欲，数学探究便是满足好奇心与求知欲的主要数学活动.数学探究是学生针对情境中的现象或问题，运用数学符号进行表达、运用数学技能进行思考、计算、作图、假设、猜想、推理与证明的数学活动. 数学探究并非是一个独立的教学活动，它是数学教学过程中的一个基本环节，它和情境相衔接. 情境是探究的前提，例如，黄金分割教学设计中，在教师呈现给学生举世闻名的雕塑——断臂的维纳斯的图片的情境中，提出“若维纳斯的高度不变，将其腿部拉长或缩短，则这幅图是否还美”的问题，会促使学生产生好奇心并主动去探究. 学生通过观察、试验后发现，假设维纳斯头顶用点A表示，脚底用点B表示，维纳斯的身高就可用线段AB表示，以图片中维纳斯的肚挤为分割点，记为点C，这样维纳斯被分成了上半身AC和下半身BC，假设AB=1，BC=x（x>0），则AC=1-x，通过探究与对比，发现断臂维纳斯最美时上半身和下半身的比例满足=，代入未知量，列出等式=，解得x=≈0.618. 由此，在用线段表示维纳斯身高、建立等式寻求最美比值的探究活动中，黄金分割点、黄金分割比、黄金分割数等概念呼之欲出.

3. 适度形式化：表征数学抽象的结果

形式化是指将抽象出的结论、规则用数学语言、符号加以表述.形式化是数学抽象中重要的一步，通过探究活动所得到的特征、关系、规律、性质等内容，经过“形式化”处理，转变成某个数学概念、公式、法则、定理或者某个问题解决模型，从而具有了数学形态. 例如在黄金分割教学过程中，学生探索维纳斯上半身与下半身长度的比例关系其实就是线段AB上有一个点C，使得=，这就得到了分割比，设AB长度为1，得到AC∶BC=≈0.618，这就是分割数，线段AB被点C分割，所以点C为分割点.由于此比例下的物体在视觉上给人一种舒适的美感，故这个数被公认为最具审美意义比例的数字，像黄金一样珍贵. 在此基础上，世人将满足=的比称为黄金分割比，将或0.618称为黄金分割数，C点称为线段AB的黄金分割点.

4. 数学应用：数学抽象素养培养的核心载体

经历知识的形成过程，能在相关情境中抽象出数学概念与数学命题，这仅是数学抽象素养形成与体现的中间层次. 能在综合的情境中抽象出数学问题，创造性地使用数学方法解决问题，并能用数学语言解释社会和自然现象，这是形成较高水平数学抽象素养的体现和保障，也是培养学生数学抽象素养的高层次教学目标. 从数学抽象素养不同水平要求的描述中可以发现，情境、抽象出数学问题、应用数学方法、应用数学语言成了关键词组. 其中，“数学应用”将这些关键词组有机地结合在一起，从而“数学应用”成了培养和评价学生数学抽象素养的核心载体，也是培养学生数学抽象素养的基本途径. 数学应用是指在具体情境中用数学知识、数学思想与数学方法解决具体问题的过程. 在此过程中，个体需要不断地对已有的数学知识与技能进行反省、抽象与重组，抽象出更一般的解题方法或问题解决模型，最终使问题得到解决. 例如，要在一座塔上找到修建观光台的黄金位置，如何去寻找这个黄金位置呢？由于黄金分割数是一个无理数，在现实情境中精确找到黄金分割点并不容易，这就需要学生对黄金分割数从代数结构上分析其几何意义. 欲构造黄金分割数，只需要构造出-1;要构造-1，就得构造. 该如何去构造这个无理数呢？我们知道直角边的边长分别为2和1的直角三角形其斜边为. 现在将塔顶端到塔底部看作线段AB，设AB为2个单位长度，作AD垂直于AB且长度为1个单位，连接BD，便构造出了BD等于. 以D为圆心、DA为半径作弧，交BD于点E，便在BD上截取出了BE等于-1. 此时如何将相关数据转化到线段AB上呢？以B为圆心，BE为半径作弧，交AB于点C，得到BC的长度为-1，AC的长度为3-. 现在，线段AC的长比上线段BC的长的值等于线段BC的长比上线段AB的长的值，为黄金分割数，由此方法找到的点C即为黄金分割点. 其实，这种作图方法最早是由古希腊数学家海伦发现并抽象出来的，因此，该方法又被称为海伦作图法. 海伦作图法将数转化为形，是数形结合思想的完美体现.

参考文献：

[1]  康德. 纯粹理性批判[M]. 邓晓芳，译. 北京：人民教育出版社，2004.

[2]  林京榕，陈清华，董涛. 數学抽象素养培养策略[J]. 数学通报，2020， 59（02）：19-22.

[3]  中华人民共和国教育部. 普通高中数学课程标准（2017年版2020年修订）[S]. 北京：人民教育出版社，2020.

[4]  赵思林. 数学核心素养的培养策略[J]. 数学通报，2019，58（05）：28-32.