一种基于滑模自抗扰控制器的风电机组变桨距控制策略

周 杨，赵毅君，赵 耀，李世军

（1.湖南工程学院 电气与信息工程学院，湘潭 411104；2.湖南工程学院 风电装备与电能变换协同创新中心，湘潭 411104；3.湖南工程学院 风力发电机组及控制湖南省重点实验室，湘潭 411104）

0 引言

风能是一种取之不尽用之不竭的可再生清洁能源，并已成为世界上规模较大的可再生能源之一.在可持续发展的大环境下，我国正在大力发展风力发电产业，风力发电相关的控制技术也得到了飞速的发展［1］.

风力发电机组的变桨距控制起着获取最大功率以及保持风机输出功率稳定等重要作用.由于风电机组的非线性、强耦合、强扰动等特性，难以给出准确的数学模型.传统的PID变桨距控制难以达到理想的控制效果.为了解决传统PID变桨距控制策略的不足，国内外学者对变桨距控制策略进行了深入研究，将神经网络控制器、滑模控制器、自抗扰控制器（ADRC）、模糊逻辑控制器、预测控制器等应用到变桨距控制中，并且取得了一定的成果.文献［2］提出了基于线性自抗扰控制器的变桨距控制策略，利用线性自抗扰控制在处理系统扰动方面的优势，保证风电机组在额定风速以上的不同风速段均有较好的控制效果.文献［3］提出了基于卡尔曼滤波器的模糊PID变桨距控制算法，与传统的PID控制和模糊控制相比，该算法控制性能有一定程度的提高，具有一定的理论价值和实际意义，但在抑制系统超调和缩短动态响应时间方面有待提高.文献［4］提出了将滑模控制器运用于变桨距控制，减小了风力发电机组系统的抖振，但在高于额定风速下的风电机组输出功率不稳定.文献［5］中提出了将神经网络理论结合传统PID控制机理，构成单神经元PID控制器，并应用于电动独立桨叶变距系统.但神经网络控制过分依赖学习样本的质量和数量，且不易在工程中实现.文献［6］中提出了一种利用模糊逻辑整定PID控制器的变桨距控制方法，当风速大于额定风速时，模糊PID控制器对风机桨距角进行调整，实现风电机组稳定的输出功率，但系统输出仍有一定程度的超调.文献［7］中提出了鲁棒经济模型预测控制的风力发电机变桨距控制策略，针对风力发电机的经济性目标以及风速误差可能导致传统控制的一系列问题，离线设计了线性反馈控制器和相应的鲁棒控制不变集，以保证风力发电系统的鲁棒性.

本文将滑模控制引入自抗扰控制中，提出了一种基于滑模自抗扰控制技术的变桨距控制方法.以风力发电机组额定转速和风机实际输出的转速作为控制器输入的信号，经过变桨距控制器调节桨距角，使风机在高于额定风速的风况下保持功率恒定.

1 风力发电机组的建模

1.1 风力机模型

由空气动力学可知，风轮在自然风中运行所获得的功率Pw和转矩Tr为：

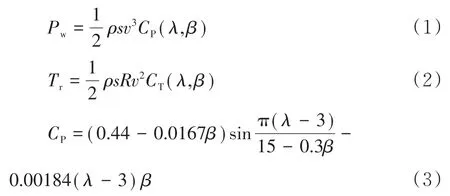
式中ρ为空气密度，R为风轮半径，s为风轮扫过的面积，v为风速，λ为叶尖速比，β为桨距角，CP为风能利用系数，CT为机械转矩系数，其中CP=λCT.

1.2 传动结构模型

本文针对双馈异步风力发电机组来建模，其简易的数学模型为：

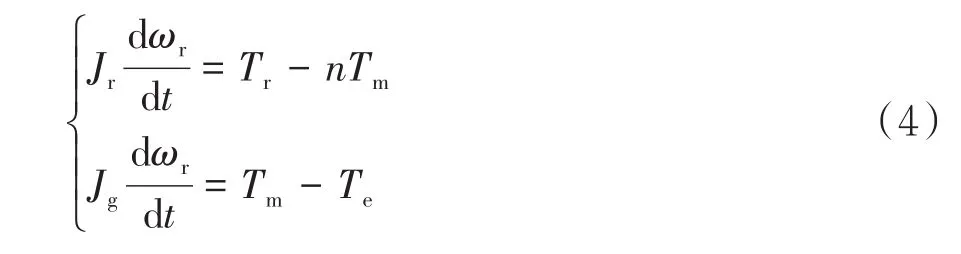
式中Tm为风轮机械转矩，Te为发电机电磁转矩，Tr为风轮输出转矩，Jr为风轮转动惯量，Jg为发电机转动惯量，ωr为风轮转速，n为齿轮箱增速比.

由式（4）可得传动链方程：

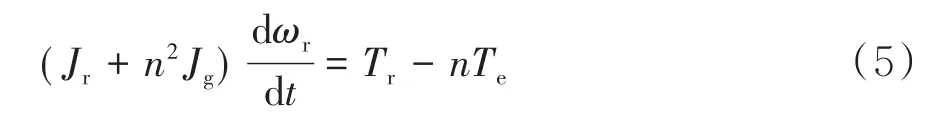
1.3 变桨距执行系统模型

变桨距执行机构可以等效为一阶模型，其数学模型为：

式中，τ为时间常数，β为实际桨距角角度，βr为给定角度.

1.4 双馈异步电机模型

为了方便计算和推导，采用理想的双馈异步电机，其数学模型为：

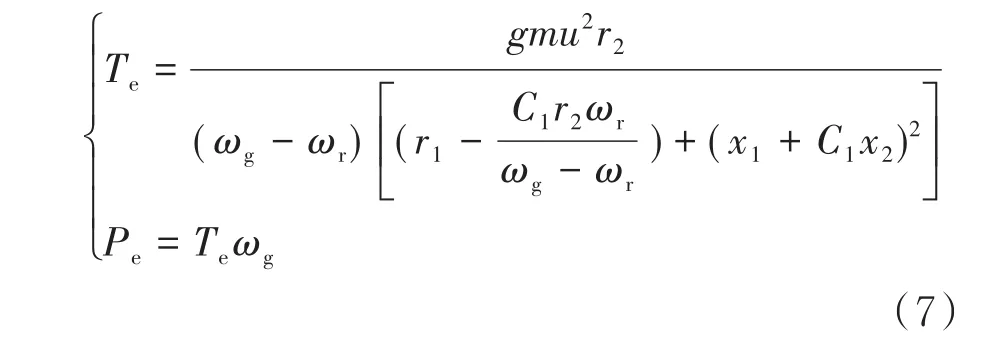
式中，g为磁极对数，m为电机相数，u1为电网额定电压（V），C1为修正系数，ωr为发电机同步转速（rad/s），r1、x1分别为定子绕组等效电阻和电抗，r2、x2分别为转子绕组等效电阻和电抗.

2 风力发电机组桨距角控制器设计

2.1 自抗扰控制算法

以一般的二阶非线性系统为例：

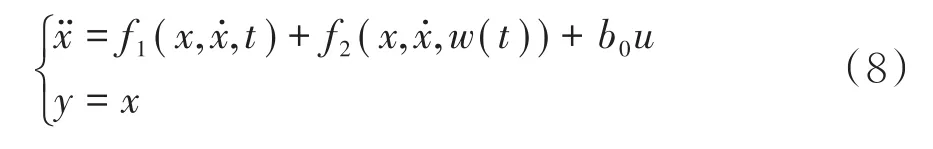
式中f1已知，w(t)为未知扰动，b0为已知参数.

（1）跟踪微分器（TD）

韩京清先生［8］所提出的跟踪微分器被大家普遍采用，具体表达式为：

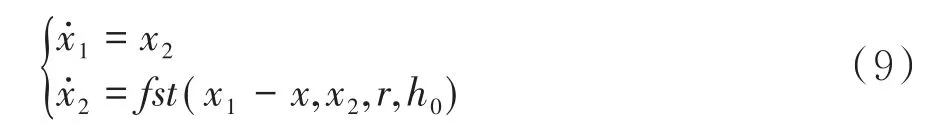
其中fst(x1-x,x2,r,h0)函数的表达式为：

式中r为速度因子，足够大时x1可以快速无超调跟踪输入信号x，x2为x1的广义导数，h0为滤波因子，适当增大可以减少x1受噪声污染的程度.

（2）扩张状态观测器（ES0）

可以把f1+f2定义为‘总扰动’，输出zi将分别跟踪xi.

其中fal(e,a,δ)函数的表达式为：

（3）非线性误差反馈控制律（NLSEF）

NLSEF是TD的输出信号x1(t)、x2(t)与扩张状态观测器（ESO）的输出信号z1、z2进行组合，产生控制量u0，然后u0和扩张状态观测器（ESO）的输出信号z3进行线性组合，最后产生控制量u并传给被控对象.

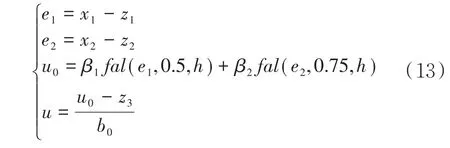
其中fal(e,a,h)函数的表达式为：

2.2 变桨距控制律设计

自抗扰控制（ADRC）中扩张状态观测器很难做到将系统的扰动完全估计，因此可以利用滑模控制对系统模型要求不高和强鲁棒性的特点，用滑模控制律来代替NLSEF改善ADRC的性能.在保证滑模控制性能的同时，滑模控制中存在的抖振问题可用ADRC消除，也提高了扩张状态观测器的观测能力.两种控制方法相结合的复合控制（SMCADRC）优势明显.

首先选择滑动面，如下式：

式中e1=x1-z1，e2=x2-z2

指数趋近律取如下形式：

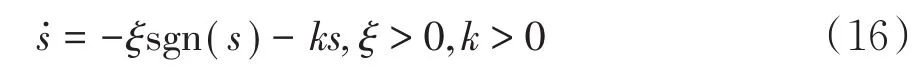
根据滑动面和指数趋近规律，可以得出：

此时，设计状态反馈控制具有3个参数：ξ,k,c.参数k的主要作用是控制系统的收敛速度，在指数趋近律中，为了保证快速趋近的同时削弱抖振，应在增大k的同时减小ξ；参数c影响滑动面上接近原点的速度.

2.3 稳定性证明

根据选取的滑模面，取李亚普洛夫函数：

对其进行求导：

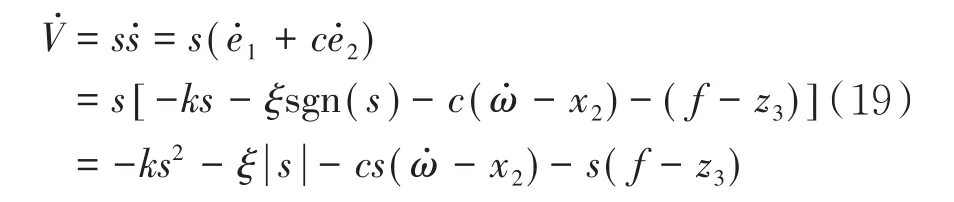
式中f为总扰动.

由于扩张状态观测器能跟踪系统状态，ω˙-x2，f-z3趋于零，ξ,k,c是大于零的常数，所以V˙＜0，因此基于滑模自抗扰控制下的系统是稳定的.

2.4 滑模自抗扰变桨距控制原理

风力发电机组滑模自抗扰变桨距控制的原理，如图1所示.

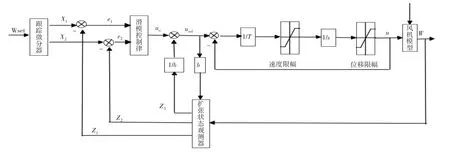
图1 控制系统原理图

滑模自抗扰变桨距控制器是由跟踪微分器，滑模控制律，扩张状态观测器构成.图1中，Wset为额定转速，X1是Wset的跟踪信号，X2是X1的微分信号，W是实际输出转速，Z1是W的跟踪信号，Z2是Z1的微分信号，Z3为跟踪总扰动.为了保证风机在运行时的安全性，在变桨距机构运行时，对叶片桨距角的大小和变化速度做了一定的限制.

3 仿真分析

基于风力发电机组滑模自抗扰变桨距控制的MATLAB仿真图，如图2所示.

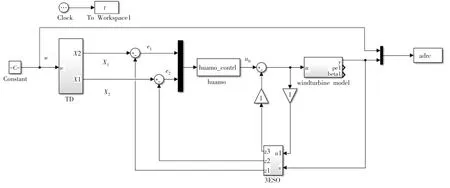
图2 系统仿真图

为验证SMC-ADRC变桨距控制器的控制效果，在simulink中搭建了一个额定功率为300 kW的双馈风电机组的数学模型.并将传统PID控制器和SMC-ADRC控制器应用到模型中.双馈风电机组的主要参数如表1所示.采用的滑模控制律系数c＝100，ζ＝0.1，k＝70.图3～图8为仿真结果.

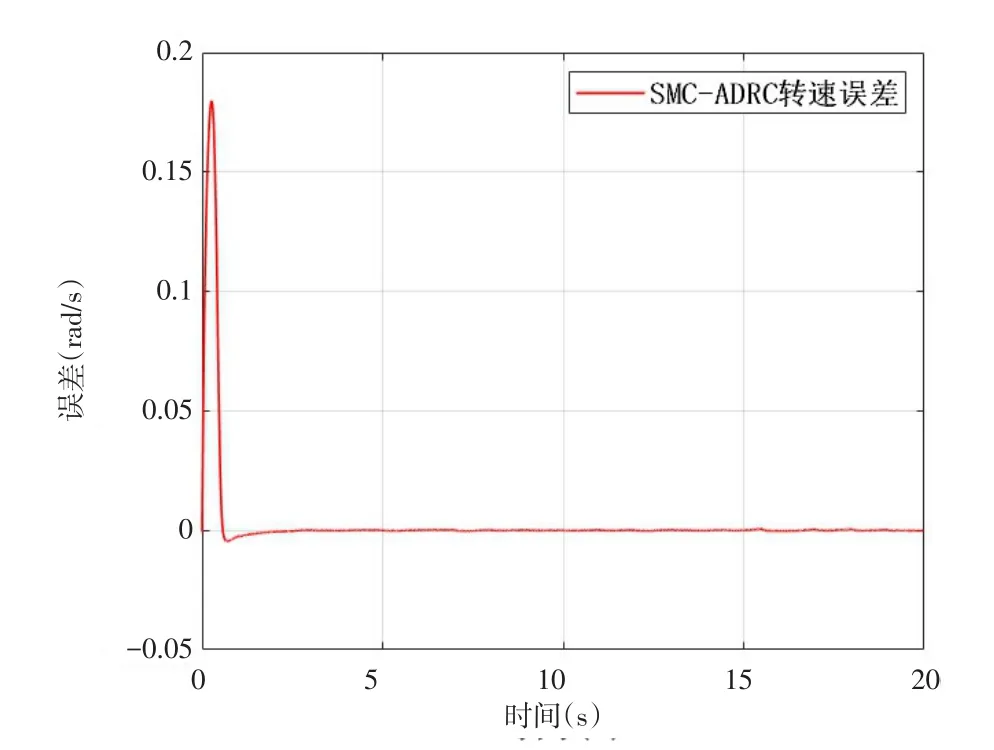
图8 SMC-ADRC转速误差图

表1 风力机以及双馈异步电机参数

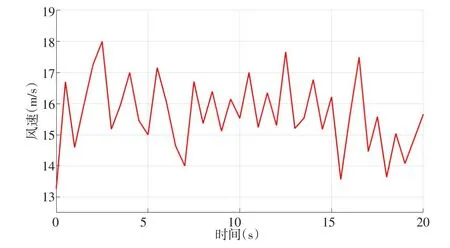
图3 随机风速曲线图

图3为风速信号，平均风速v>11 m/s，图4为基于SMC-ADRC控制策略控制下的风力机桨距角输出图.结合图3和图4，当风速发生变化时，风力发电机的桨距角能够很好地给出相应的变化，桨距角的变化幅度也在合理范围之内.

图4 SMC-ADRC桨距角变化图

从图5～图7可以看到，在风速高于额定风速时，本文设计的SMC-ADRC控制变桨距系统相比于传统PID控制变桨距系统可以快速地减小风力机转速和输出功率超调，响应速度快，系统输出更加平滑.

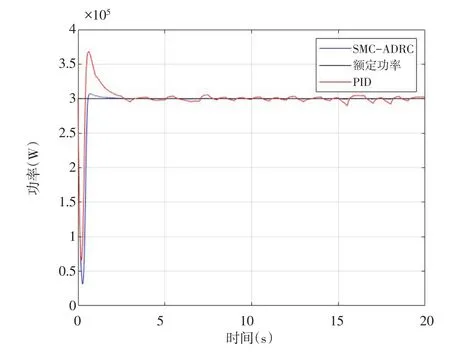
图5 输出功率图

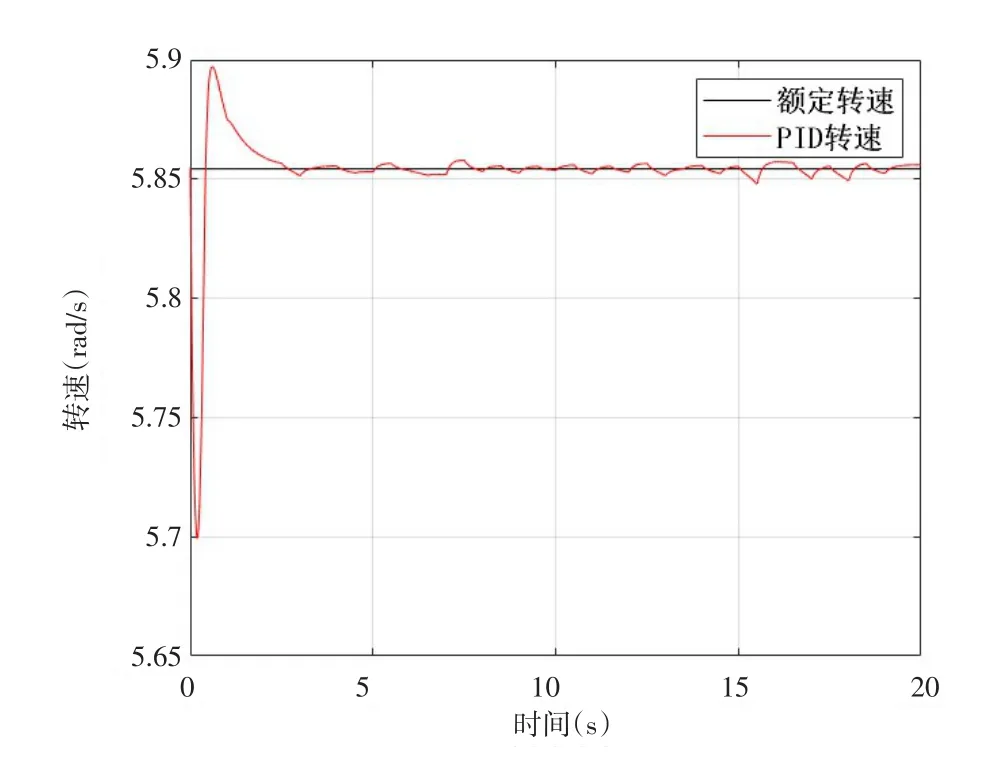
图6 PID转速图

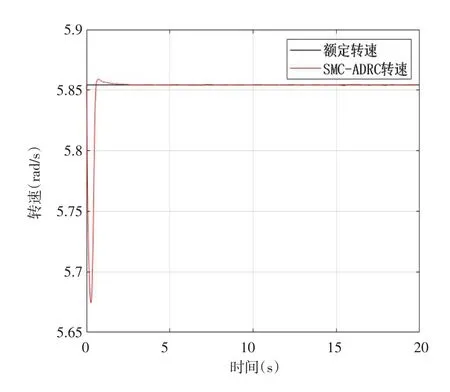
图7 SMC-ADRC转速图

从图8的转速误差曲线可以看出，基于SMCADRC控制系统可以快速地使转速误差控制在合理范围内，证明了滑模自抗扰控制器的有效性.

4 结论

（1）使用扩张状态观测器（ES0）可以对风力发电机的非线性、风速变化等各种扰动进行估计，用滑模控制律来代替自抗扰控制技术中的NLSEF，仿真结果证明在解决了滑模控制存在的抖振问题的同时，也很好地对各种干扰进行补偿处理，提高了自抗扰控制器的性能.

（2）将本文提出的控制策略与PID控制策略通过Matlab/Simulink软件仿真对比，在高于额定风速的风况下，采用滑模自抗扰控制的变桨距系统有着明显的优势，可以使风力发电机系统的输出功率快速稳定在300 kW附近.仿真结果证明了本文所设计的控制器具有更好的控制能力.