吸附对石墨烯量子点电子结构和光学性质的影响

田梦园，陈 桥

（湖南工程学院 计算科学与电子学院，湘潭 411104）

0 引言

2004年英国曼彻斯特大学Geim和Novoselov等人利用机械剥离法从石墨中分离出石墨烯，开启了二维纳米材料的新篇章［1-4］.石墨烯由sp2杂化的碳原子以六角蜂窝状网格排列而成［5］，具有D6h对称性，单个原胞中有两个碳原子，相邻两个碳原子之间的距离约为1.42 Å.石墨烯具有优良的电学性能，其载流子迁移率室温下可达到2.5×105cm2V-1s-1，且迁移率远高于传统的硅半导体材料［6］.石墨烯的电导率可达106S·m-1.此外，石墨烯还具有优异的热学、力学和光学特性［7，8］.其杨氏模量高达1 TPa［9］，室温下的热导率超过3000 W/m·K［10］，且单层石墨烯的透光率可达97.7%［11］.这些优良的性质使石墨烯在微电子器件、光学器件、电池能源等领域具有良好的应用前景［12-16］.但是，由于石墨烯是零能隙半金属材料，基于石墨烯制备的场效应晶体管开关比相对较低［17］.因此打开一个可控的能隙是石墨烯研究最重要和急迫的主题之一.目前，对石墨烯能隙调控的方法主要有表面吸附［18］、掺杂［19］以及衬底调控［20］等.其中，表面吸附是实验上较为常用的一种方法.因为，其在保留石墨烯高载流子迁移率的同时，有效地破坏石墨烯的对称性，从而打开能隙［21］.

量子点是一种在三个空间维度上束缚激子的低维半导体纳米结构，有时也称为人造原子［22］.量子点的横向尺寸一般在1～100 nm之间，垂直厚度为几层.因受到三维量子限域效应的影响，量子点的能带结构呈分立的形式，其所对应的波函数在空间上位于量子点中，并且延伸于各个晶格周期中.由于量子点独特的能级结构，使其可以表现出很多新奇的物理性质，如量子尺寸效应、非线性光学效应等，这对于研制新型光学和电子器件具有重要的意义.目前，石墨烯［23-27］、单层和双层磷稀［28-32］以及过渡金属硫族化合物［33-38］等新型二维材料构造的量子点得到了广泛的研究.

在最近的研究中，有学者基于紧束缚近似方法研究了表面吸附对石墨烯纳米带来的影响.研究表明当石墨烯纳米带中心散射区域吸附浓度为100%时，狄拉克点周围打开能隙，且能隙随吸附浓度的升高而逐渐增大［39］.此外，Schedin等［40］人在实验上证明了石墨烯对气体分子（如H2O、NO2、CO和NH3等）具有一定的灵敏度.Zhou等［41］人预测了石墨烯吸附氧原子浓度为9.4%时，能隙达到最大（约0.952 eV），且吸附浓度的改变会对能隙大小产生影响.但是，目前吸附对石墨烯量子点电子结构和光学性质的影响一直未被研究.因此，本文主要考虑了锯齿状六边形石墨烯量子点，研究吸附对其电子结构和光学性质的影响.主要结论如下：（1）当吸附浓度为100%时，锯齿状六边形石墨烯量子点在零能附近存在能隙.（2）石墨烯量子点尺寸较小时，能隙由于吸附原子的作用被关闭.但是，能隙随着吸附原子与碳原子间耦合强度的增强又被打开.（3）零能位置的态密度随着吸附浓度的升高先增大后减小.并且，光吸收峰随着吸附浓度的升高发生蓝移.

1 研究模型及计算方法

图1给出了石墨烯量子点结构示意图，在锯齿状六边形石墨烯量子点的每个碳原子上吸附同一类型的原子.为了研究吸附对锯齿状六边形石墨烯量子点的电子结构和光学性质的影响，采用最近邻紧束缚模型描述石墨烯量子点的主要物理性质.考虑了量子点的尺寸、吸附原子与碳原子间耦合强度γ以及吸附浓度的影响.因此，该哈密顿量可以写为：

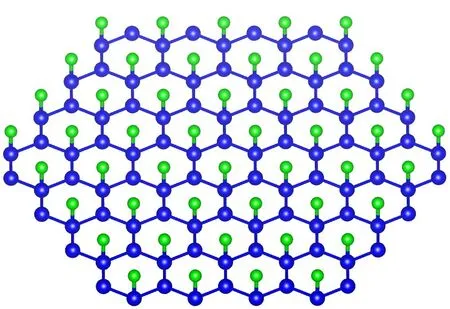
图1 吸附锯齿状六边形石墨烯量子点的结构示意图

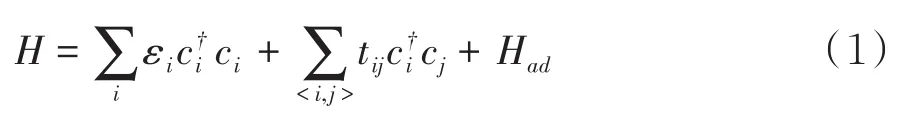
其中，εi表示石墨烯碳原子第i位格点处的在位能，＜i,j＞表示最近邻位置，为格点i（j）处电子的产生（湮灭）算符，且tij=t为最近邻原子的跃迁能.Had表示吸附原子与碳原子之间的耦合，记为：

其中，εα为吸附原子在格点α处的在位能，为吸附原子在格点α处的产生（湮灭）算符，pα为吸附原子与碳原子的耦合位置，γ表示吸附原子与碳原子间的跃迁能.在计算中，选取的相关参数ε=0，t=-3.033 eV［42］.

石墨烯量子点的态密度是由一系列的函数δ求和得到的，态密度更好地展示了量子点中的能级分布，其表达式为：

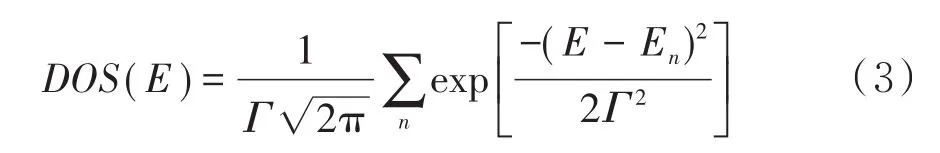
其中Γ是高斯展宽，Eп表示第n个本征态的本征值.

假设光沿着在石墨烯量子点的()x,y平面上发生偏振，则可以采用如下的公式计算石墨烯的光吸收能谱［43-44］：

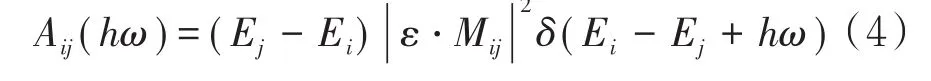
其中Ei（Ej）分别表示格点（i格点j）上的能量，ε为光入射方向余量，Mij=＜j||r i＞代表格点i与j之间的跃迁.

六边形石墨烯量子点中的波函数是通过对紧束缚哈密顿矩阵进行数值对角化而获得的，所有的数值计算均利用由创建Python开发程序包的Kwant［45］和Pybinding完成.另外，还将得到的波函数结果代入态密度和光吸收能谱的计算中.

2 结果与讨论

在图2中，研究了吸附对锯齿状六边形石墨烯量子点电子结构的影响，其中量子点的尺寸为Nz=11.由图2（a）可知，在锯齿状六边形石墨烯量子点中能隙为零，并且在零能处存在边缘态.但是，当吸附浓度为100%时，量子点在零能附近存在明显的能隙，如图2（b）所示.为了解量子点能隙打开的原因，计算了量子态对应的概率密度.研究表明，零能附近电子集中分布在量子点的中央区域，在零能附近存在体态，边缘态被排斥到正负1.11 eV以外的区域（如图2（b）中量子态α和β的x-y平面所示），且量子点能隙打开.进一步研究表明，零能附近的体态位于吸附原子上，边缘态在石墨烯碳原子和吸附原子上同时存在（如图2（b）中量子态α和β的x-z平面所示）.因此，吸附会导致锯齿状六边形石墨烯量子点在零能附近的能隙打开.

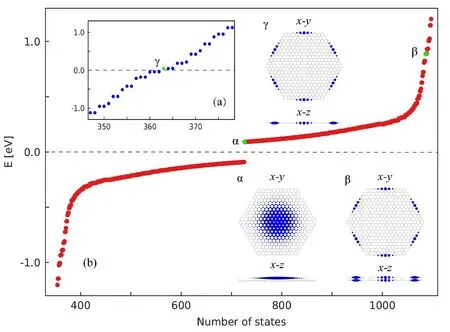
图2 锯齿状六边形石墨烯量子点的本征能谱图

图3给出了不同吸附原子与碳原子间耦合强度下锯齿状六边形石墨烯量子点的态密度及其所对应的概率密度.根据文献［24］，计算了与上文不同尺寸六边形石墨烯量子点的态密度，这里选取量子点的尺寸为Nz=6.从图中可以看出，锯齿状六边形石墨烯量子点在零能附近存在明显的能隙.但是，当吸附浓度为100%时，且在吸附原子与碳原子间的耦合强度为γ=0.1 t的情况下，零能附近的能隙关闭.而当吸附原子与碳原子间的耦合强度为γ=0.6 t时，在零能附近的能隙又被打开.为了解能隙开合的原因，在图3（a）、图3（b）和图3（c）上选取了五个峰，并用数字1～5标记.随后，计算了这五个峰对应的概率密度，如图3（d）所示.其中，波函数、波函数以及波函数分别对应于吸附原子与碳原子间耦合强度为γ=0、γ=0.1 t和γ=0.6 t的六边形石墨烯量子点.研究表明，在吸附原子与碳原子间耦合强度为γ=0的六边形石墨烯量子点中，零能附近存在边缘态.而对于吸附原子与碳原子间耦合强度为γ=0.1 t和γ=0.6 t的六边形石墨烯量子点，在零能附近则为体态.因此，由于吸附原子的作用，导致量子点能隙被关闭.但是，随着吸附原子与碳原子间耦合强度的增强，能隙又被打开.

图3 不同吸附原子与碳原子间耦合强度情况下锯齿状六边形石墨烯量子点的态密度及其对应的概率密度，量子点的尺寸为Nz=6（.a）、（b）和（c）是锯齿状六边形石墨烯量子点的态密度，其中吸附原子与碳原子间耦合强度分别为γ=0、γ=0.1 t和γ=0.6 t，数字1-5标记了不同吸附原子与碳原子间耦合强度下六边形石墨烯量子点中零能附近的峰（.d）六边形石墨烯量子点对应于数字1-5的概率态密度.在计算中，采用高斯展宽因子Γ=0.01 eV

在图4中，讨论了不同吸附原子与碳原子之间的耦合强度对锯齿状六边形石墨烯量子点光吸收能谱的影响.因为石墨烯量子点沿x和y方向的光吸收能谱几乎相同，所以为了简单起见，采用沿x方向的偏振光［46］.图4（a）、图4（b）以及图4（c）的吸附原子与碳原子间耦合强度分别为γ=0、γ=0.3 t和γ=0.6 t.研究表明，随着吸附原子与碳原子间耦合强度的增强，光吸收峰会逐渐向着高能的方向移动（即蓝移）.进一步研究表明，光吸收峰移动的距离与六边形石墨烯量子点在零能附近能隙打开的宽度是相同的.并且，随着吸附原子与碳原子间耦合强度的增强，光的吸收强度会逐渐减弱.

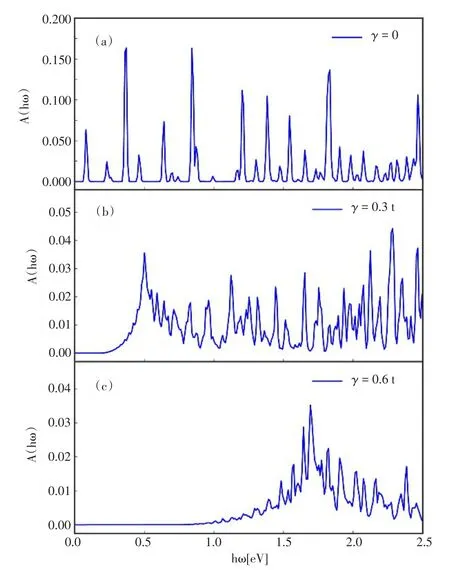
图4 不同吸附原子与碳原子间耦合强度情况下锯齿状六边形石墨烯量子点的光吸收能谱，图4（a）、（b）和（c）的吸附原子与碳原子间耦合强度分别为γ=0、γ=0.1t和γ=0.6 t.其中，量子点的尺寸为Nz=11，采用的高斯展宽因子与图3相同

图5计算了在不同吸附原子与碳原子间耦合强度作用下六边形石墨烯量子点的态密度.其中，图5（a）和图5（b）中量子点尺寸分别为Nz=11和Na=7.从图5中可以看出，无论六边形石墨烯量子点的边缘类型是锯齿状边界还是扶手椅状边界，六边形石墨烯量子点在零能附近的能隙都会随着吸附原子与碳原子间耦合强度的增强而逐渐增大.由上文可进一步得知，当吸附浓度为100%时，由于吸附原子的作用，六边形石墨烯量子点在零能附近存在能隙，且能隙随着吸附原子与碳原子间耦合强度的增强而增大.

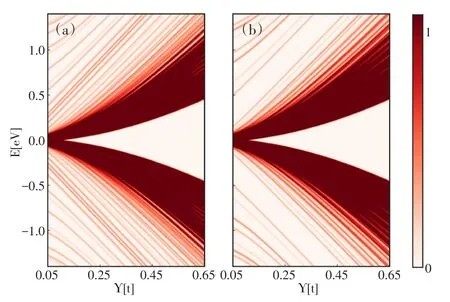
图5 六边形石墨烯量子点在不同吸附原子与碳原子间耦合强度作用下的归一化态密度的等高线图.（a）锯齿状六边形石墨烯量子点，其中量子点尺寸为Nz=11，（b）扶手椅状六边形石墨烯量子点，其中量子点尺寸为Na=7.这里采用的高斯展宽因子与图3相同

图6计算了不同吸附浓度下锯齿状六边形石墨烯量子点的态密度.由上文可知，锯齿状六边形石墨烯量子点在零能处能隙为零.如图6（a）、图6（b）和图6（c）所示，零能位置的态密度随着吸附浓度的升高先增大后减小.为了更清楚了解零能位置态密度的变化情况，图6（d）展示了六边形石墨烯量子点在零能位置态密度随吸附浓度变化的规律.经研究表明，当六边形石墨烯量子点吸附少数的原子时，在零能附近的量子态简并度增强，导致零能位置的态密度随吸附浓度的升高而逐渐增大.当吸附原子数与碳原子数的比为1∶2时，零能位置态密度达到最大.但是，随着吸附浓度继续升高，吸附原子的作用就会逐渐增强，从而导致零能位置的态密度减小.当吸附原子数与碳原子数相等时，零能位置的态密度为零，且在零能附近打开能隙，与图2所得结论一致.

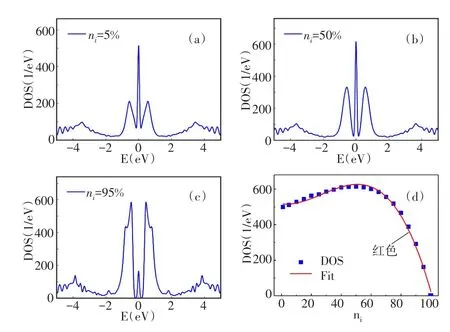
图6 不同吸附下浓度锯齿状六边形石墨烯量子点的态密度.图（a）、（b）和（c）吸附浓度分别为ni=5%、ni=50%和ni=95%，图（d）六边形石墨烯量子点在零能处的态密度峰随吸附浓度的变化规律，红色实线对其进行拟合.其中，选取的尺寸与图2相同，采用的高斯展宽因子Γ=0.05 eV

在图7中，研究了不同吸附浓度对锯齿状六边形石墨烯量子点光吸收能谱的影响.这里，选取的吸附原子与碳原子间耦合强度为γ=0.6 t，吸附浓度分别为ni=25%、ni=50%和ni=75%.由上文可知，当吸附浓度为ni=100%时，锯齿状六边形石墨烯量子点的光吸收峰随吸附原子与碳原子间耦合强度的增强而发生蓝移.从图7中可以看出，随着吸附浓度的升高，光吸收峰向高能的方向移动，也发生了蓝移.

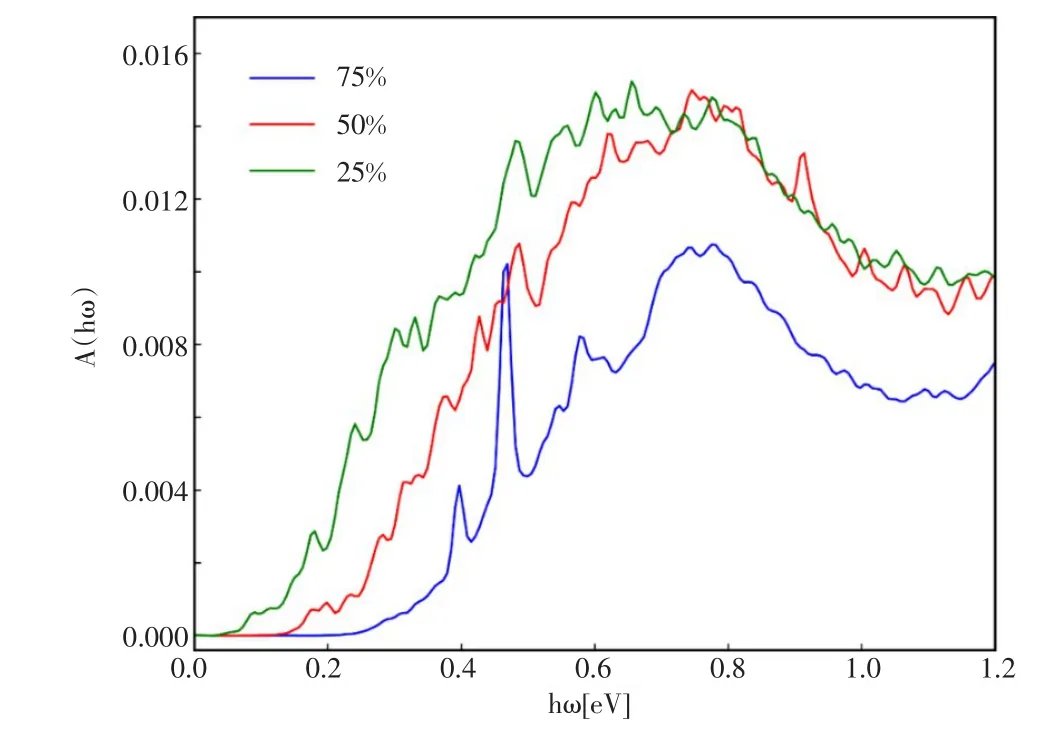
图7 不同吸附原子浓度锯齿状六边形石墨烯量子点的光吸收能谱.其中，量子点的尺寸Nz=11，吸附原子与碳原子间耦合强度为γ=0.6 t，采用的高斯展宽因子与图3相同

3 总结

本文基于紧束缚模型，详细讨论了吸附对锯齿状六边形石墨烯量子点电子结构和光学性质的影响.首先，计算了锯齿状六边形石墨烯量子点的能级、波函数以及态密度，然后利用能级和波函数计算出相应的六边形石墨烯量子点光吸收能谱.研究结果表明，在吸附浓度为100%的情况下，零能附近存在体态，边缘态被排斥到远离零能的区域，且锯齿状六边形石墨烯量子点在零能附近能隙打开.在量子点尺寸较小时，零能附近的能隙由于吸附原子的作用被关闭，而随着吸附原子与碳原子间耦合强度的增强，零能附近的能隙又被打开.量子点的光吸收峰会随着吸附原子与碳原子间耦合强度的增强发生蓝移.另外，锯齿状六边形石墨烯量子点在零能位置的态密度随着吸附浓度的升高先增大后减小.并且，随着吸附浓度的升高，量子点的光吸收峰发生蓝移.