基于机器学习聚类算法的城市公交车站点优化分析

向 玲，张小威，唐志航，杨 莹，马倩茜

（湖南工程学院 计算机与通信学院，湘潭 411104）

0 引言

目前，大城市交通拥堵成为普遍现象［1-3］.因此对占比最大的城市公交车的优化管理也成为必然趋势［4］.由于公交车刷卡数据不完善，而刷卡数据又比较庞大和密集，因此需要对刷卡数据进行聚类分析［5］.通过对三种聚类算法（DBSCAN、k-means、DIANA）的对比，发现DBSCAN密度聚类效果最佳，能够获得科学准确符合现实要求的站点位置.同时，结合统计与概率学的泊松分布规律等知识进行分析预测，获得人们在各个站点的出行规律，并构建OD矩阵模型，为城市公交车站的优化提供合理建议.

1 挖掘建模的设计

研究主要分五个模块：挖掘目标模块、数据抽取模块、数据探索与预处理模块、挖掘建模模块、模型应用模块.总体思路如图1所示.

图1右边站点数据是从抽取数据中聚类分析所得，上下车人数是由OD矩阵式优化模型分析计算出的数据.左边的市民出行规律和城市公交车优化建议是本项目的挖掘目标.

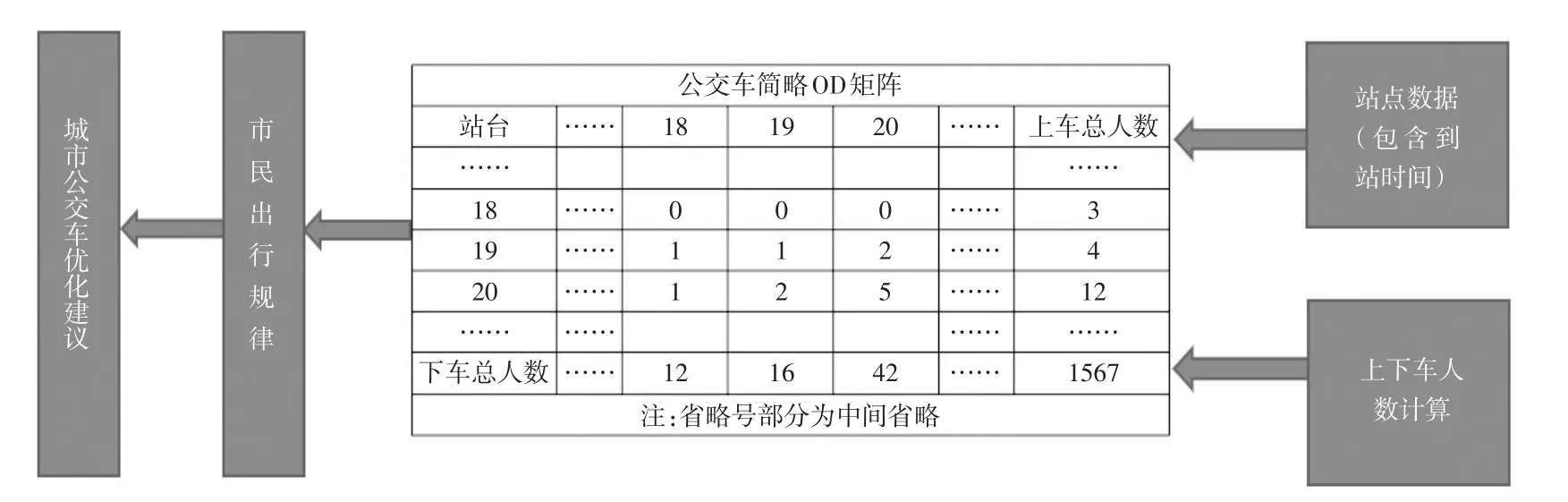
图1 总体思路图

根据上面五个模块设计出本研究的总体开发 流程，总体流程图如图2所示.

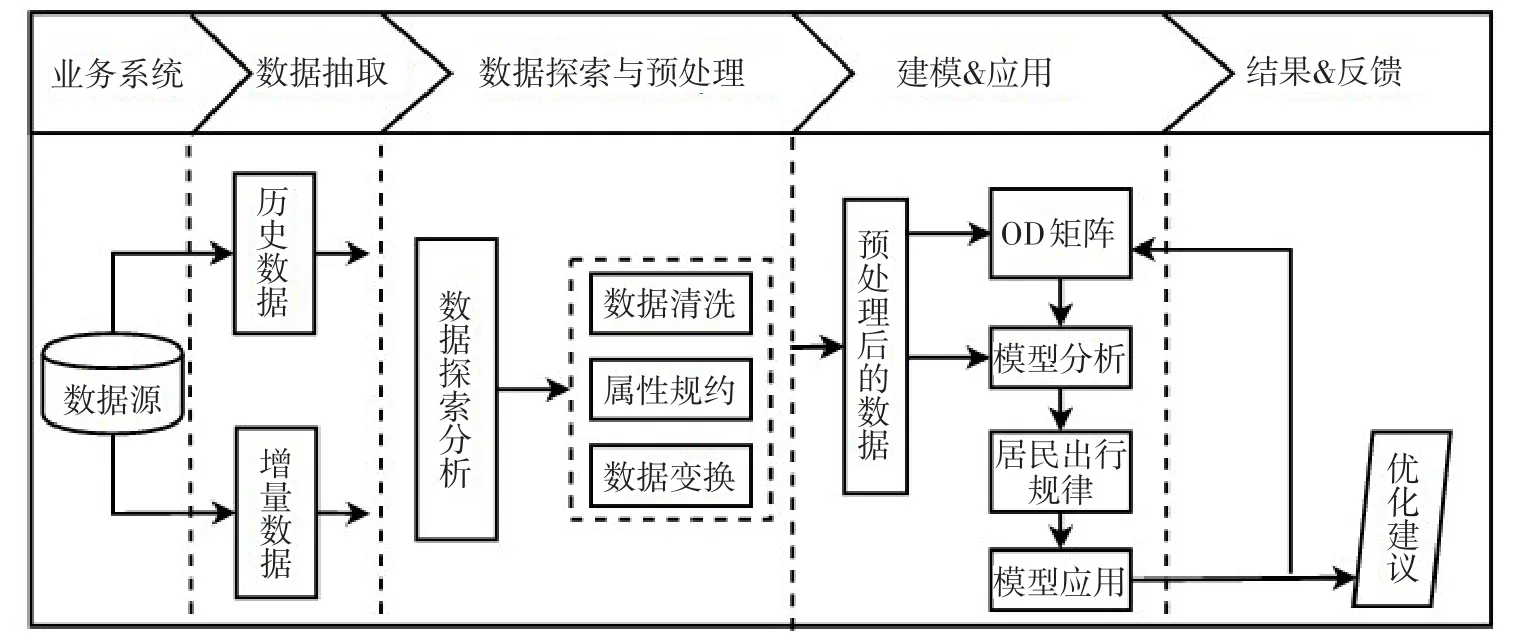
图2 总体流程图

第一步：查找数据资源获取数据源.

第二步：抽取与深圳市某路公交站点相关的原始数据，主要有地面公交车刷卡数据以及地面公交车GPS监控数据等.

第三步：数据探索与预处理，对从数据源中抽取出来的数据进行数据清洗、属性规约和数据变换.

第四步：建模与应用，本研究通过机器学习的聚类算法分析和建模，用的聚类模型是DBSCAN聚类模型，DBSCAN聚类用的是dbscan函数.建模完成之后替换另外两种算法重新分析并对比效果.

第五步：结果与反馈，通过构建的OD矩阵模型分析，得出居民出行规律，最后反馈结果、给出优化建议并进行模型优化.

1.1 城市公交车优化分析模型

城市公交车优化分析模型流程图如图3所示.

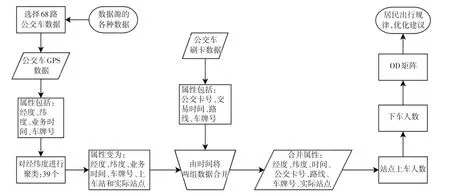
图3 城市公交车优化分析模型流程图

1.2 聚类分析

将预处理的公交车数据带入聚类模型进行聚类［6-7］，得到相应的聚类结果后，为数据贴上标签.更换聚类模型的聚类算法，重新进行聚类，对比分析不同聚类算法的效果和特性［8-9］.

1.3 下车人数预测统计

本研究利用上车人数计算下车人数，每个站点的下车人数为Dj.

其中，Dj为j站下车人数；Sk为k站上车人数；Pkj为k站上车，途径j-k站下车的概率.

最终居民公交出行的出行站数概率计算公式为：

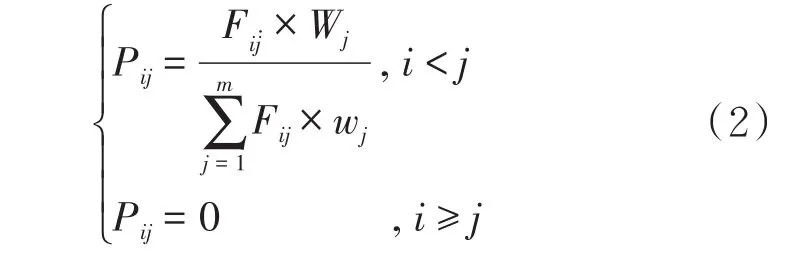
其中，Fij是居民公交出行的出行站数概率服从的泊松分布，Wj是站点对乘客的吸引权重.

居民公交出行的出行站数概率服从的泊松分布（假设），Fij计算公式如下：

其中，λ为公交路线出行途经的站点数的数学期望；Wj为j站权重；Fij为i站上车途经j-i个站点下车的概率.

站点对乘客的吸引权重Wj计算公式如下：

Wj为j站的吸引权重，其中Sk为k站上车人数.

1.4 构建OD矩阵

通过聚类和上面人流量预测模型分析出OD数据［10］，得到OD调查结果，OD调查结果通常用一个二维表格表示，纵（Y）站点表示上车站台，横（X）站点表示下车站台，矩阵中的数表示在Y站上车X站下车的人数，最右侧是各站点上车总人数，最后一行是各站点下车总人数，最后一个数据为该路公交车的总人数.利用二维数组的形式接收并输出OD矩阵［11］.

2 数据准备与处理

在实验开始前，首先获取数据源，数据源中提供的数据有：出租车GPS监控数据、地面公交车GPS监控数据、地面公交车刷卡数据、地铁站刷卡交易数据；与城市公交车站点相关的原始数据主要有地面公交车GPS监控数据以及地面公交车刷卡数据等，相关数据有5万多条.需要对数据源中抽取的数据进行数据清洗、属性规约和数据变换.

（1）数据清洗：从业务以及建模的相关需要方面考虑，筛选出需要的数据.包括缺失值处理、去除重复数据项、去除模糊数据项.

（2）属性规约：属性选择后的数据集，如表1所示.

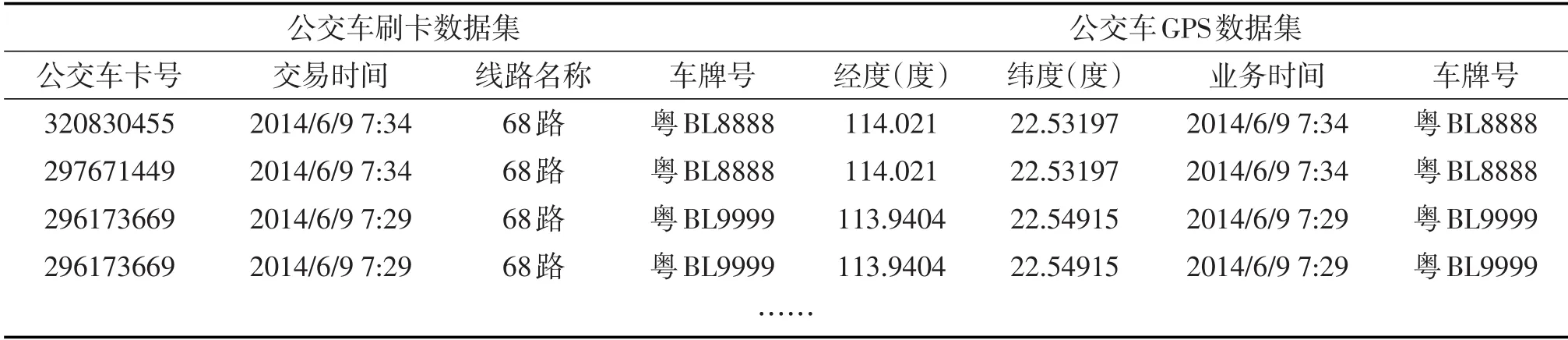
表1 预处理后的数据集

3 实验结果及分析

在对数据进行抽取和预处理后，从五万多条数据中筛选出某路公交车五天的相关刷卡数据1650条，将对筛选出来的数据进行挖掘建模.刷卡数据比较密集，为了更好地体现路线上的位置关系，实验用到了高德开放平台做可视化处理.又知道某路公交车当时的实际站点有56个，从密集的刷卡数据中我们无法直接得出数据属于前后哪个站点，因此我们对刷卡数据进行聚类，同时也对某路公交车站点进行优化.

（1）对刷卡数据进行聚类，因为是对公交车站点进行优化分析，无法直接得知聚类个数，而kmeans和DIANA聚类都需要提前确定聚类个数，所以先需要使用密DBSCAN度聚类进行优化分析.聚类过程需要不断更改并测试DBSCAN的参数（扫描半径eps、阈值min_samples），通过对聚类效果评估分析最终确定参数值，聚类评估包括对聚类产生异常值点（不和其他密度相连）个数、聚类个数、聚类实际位置等.

实验测试分析最终确定参数eps=0.0011、min_sample=3，聚类个数为39个，即最终优化的站点个数.DBSCAN密度聚类最优结果如图4所示.

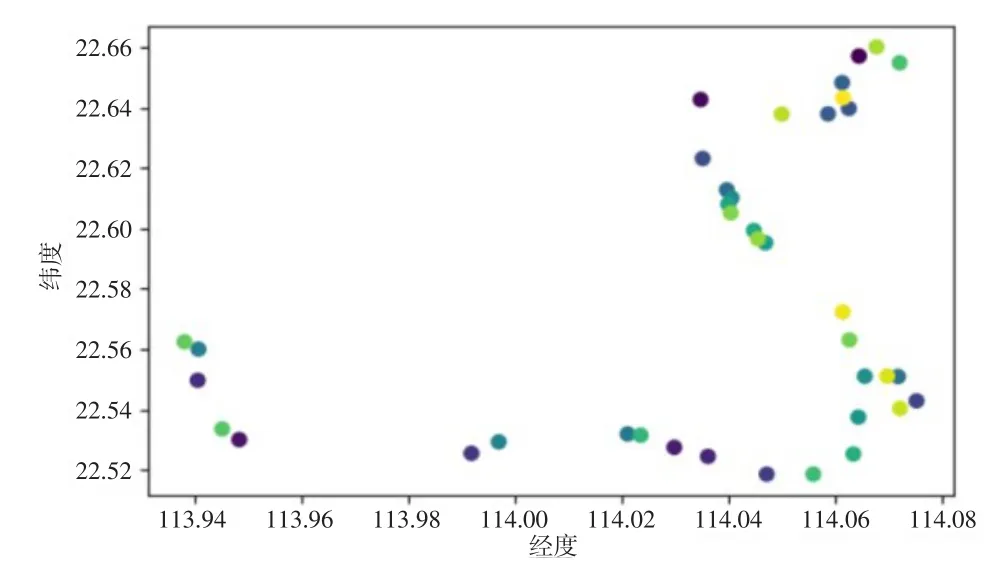
图4 DBSCAN聚类效果图

（2）根据上面优化分析得到的聚类个数，在利用K-means聚类（其中n_clusters=39），得动态聚类K-means，聚类结果如图5所示.

图5 K-means聚类效果图

利用肘方法对K-means进行评估分析，得到质点距离平方和（SSE）与聚类个数K的关系图，如图6所示.

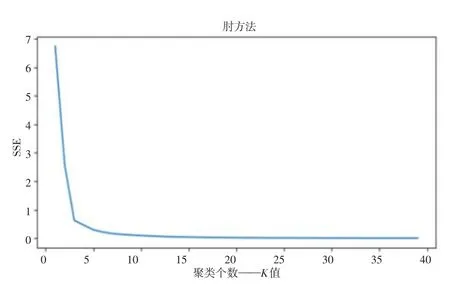
图6 肘方法评估K-Means聚类图

根据肘方法评估原理，用K-means对此数据集聚类获得最佳K值须取3～5之间，也就是聚类个数在3～5个最好，这明显不符合实际要求.

（3）再使用分裂的层次聚类DIANA聚类，结果如图7所示.

图7 DIANA聚类效果图

根据聚类算法评估指标分析，得出三个聚类算法的聚类评估情况如表2所示.根据聚类评估的各项指标分析，密度聚类DBSCAN的聚类效果更佳，更适合这种交通线路分布结构的数据集的聚类.

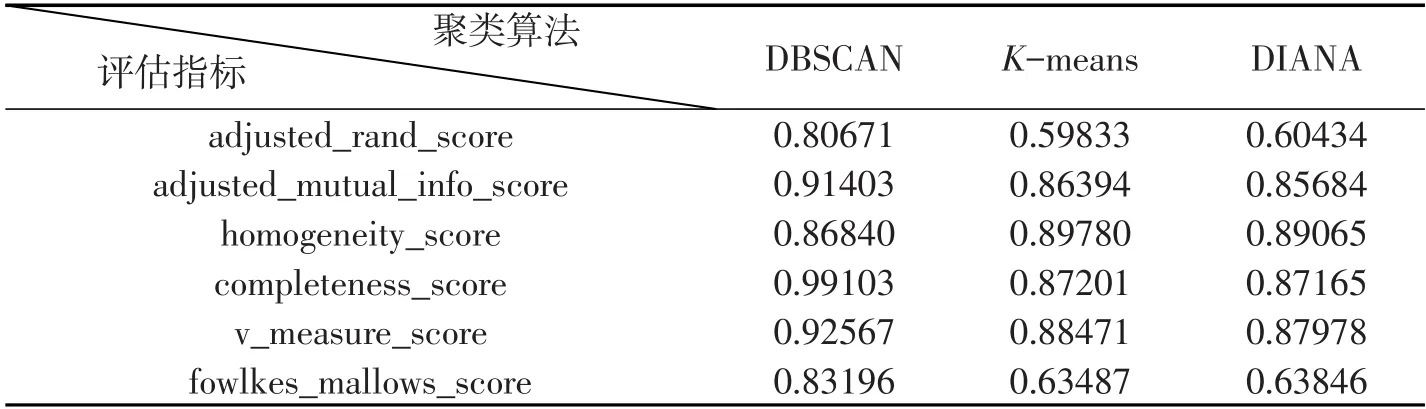
表2 聚类评估指标表

（4）根据挖掘模型我们还可以将数据进行时段分析，分析得到时段的OD矩阵，分析得到更加细致的规律.在总OD矩阵表中该矩阵是典型的上对角矩阵，只有右上半边有数据且前七列没有数据，为了更清楚直观，实验将OD矩阵的上下车总人数用柱状图表示如图8、图9所示.

图8 OD矩阵68路公交车上车人数预测分析柱状图

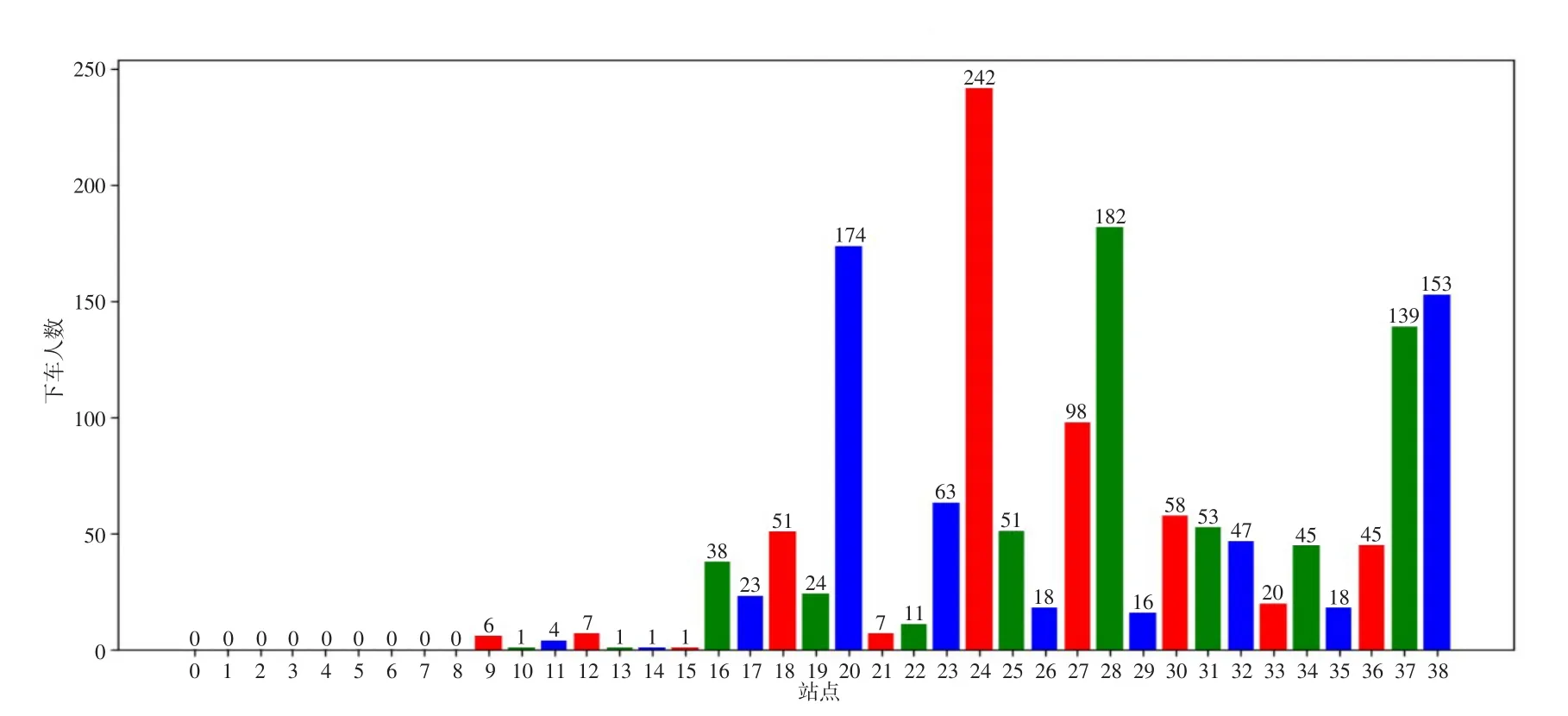
图9 OD矩阵68路公交车下车人数预测分析柱状图

根据OD数据可以得到下面规律和优化建议：

（1）居民出行规律

①人们对公交车的需求还是比较大的，几乎百分之八十的人依然选择了传统城市公交车出行；

②居民乘坐公交车出行一般距离比较远，一般都至少超过九站才下车；

③居民在某路公交车中在1、7、9等位置的站点上车人数较多，在20、24、28、37、38等位置站点下车人数较多；

（2）城市公交车的优化建议

①在上下车人数较多路段可以增设站点或者适当改变公交车的停靠方式（把直线式改为港湾式），缓解上下车压力；

②某路公交车的实际站点56个，可缩减为39个；

③在某公交车路线中，可以看到在1、7、9、20、24、28、37、38等出行人数较多的站点设置已经非常密集了，因此无须再增设，可以将这些站点中的直线停靠方式改为港湾式停靠.

4 结论

采用机器学习聚类算法对城市公交车站点进行优化分析，针对公交车的刷卡数据密度等因素，对公交车站点进行有效的选址和压缩，同时构建上下车人数预测模型，分析出居民出行的OD矩阵.此优化可以有效降低公交车运输成本，人们出行也更加方便，有利于缓解交通拥堵.另外，还可以为公交汽车公司提供辅助决策参考，在乘客少的路段可以提高行驶速度以提高效率、在上下车人数多的站点设置港湾式停靠方式等.本研究是针对城市公交车站点的设置进行的优化分析，同时本研究对火车、高铁、BRT和轻轨地铁等交通网络规划有很高的参考价值.