符号序列多阶Markov分类在银行客户风险预测中的应用

程铃钫，陈黎飞，赖晓燕，林燕

（1.福建农林大学 金山学院，福建 福州 350002；2.福建师范大学 数学与计算机科学学院，福建 福州 350117）

0 引言

当今，由于金融行业突飞猛进的发展，银行可以从庞大的数据库中挖掘出很多潜在的价值，譬如银行账户资产信息、用户个人以及交易等信息，以便提高银行业务水平和运营收益。然而在投资主体越发复杂、多元的背景下，必须高度重视风险预警工作的重要性。由此正确预测银行客户风险是一项非常重要的风险管理任务，其具有重要的意义[1-2]。

早期的银行破产预测的模型较多采用传统计量和统计方法。近年来，伴随人工智能的不断发展，机器学习、数据挖掘技术得到广泛推广，银行风险预测因此得到行之有效的方法。

目前国内较多学者首先通过改进apriori算法、银行客户信息特性，以实现快速响应和智能分析。然后采用非结构化手段存储客户各项关联信息，并对信息进行清洗、转化、标准化等处理后将有用的信息存储在数据库中，为下一步的数据分析提供数据源。最后构建客户风险评估和预测的模型[3-5]。然而，目前大多数模型都应用于国外，国内大多数学者的研究始终停留在定性分析的层面，尚未研究出与国情相匹配的完整模型，由此银行在应用模型时时常遇到亟待改进的局限。

1 马尔科夫模型

隐马尔科夫模型（简称“HMM”）是结构最简单的动态贝叶斯网，其中的变量分为两组，第一组是状态变量{y1，y2…yn}，表示第i时刻的系统状态。第二组是观测变量{x1，x2…xn}，其中表示第i时刻的观测值。模型中存在多个状态相互之间转换，观测变量Xi可以是离散型也可以是连续型[6-9]。我们假定其取值范围X为{o1，o2…om}。

从图1可以看出，变量之间存在依赖关系，t时刻状态yt仅依赖于t-1时刻的状态yt-1，与此前t-2个状态无关[10]。由此我们推出新的分布式：

隐马尔科夫需要的3个参数分别是：

表示在任意时刻t，若状态为Si，则在下一时刻状态为Sj的概率。

表示在任意时刻t，若状态为Si，则观测值Oj被获取的概率。

银行客户管理中客户行为通常采用离散符号表示，一段时间内的客户行为即构成一条符号序列。符号数据包含结构化的符号属性（类属型）数据和非结构化符号序列数据，对符号数据进行分类是必要过程。目前得到广泛使用的支持向量机、决策树、近邻（nearest neighbor，NN）分类、基于概率模型的分类的机器学习方法多针对向量型数据，同时现在的符号序列Markov分类多数是基于固定阶Markov模型（n-阶Markov模型），而阶数n与所提取的序列结构特征息息相关，其值将直接影响分类器的性能，最终会影响预测的结果，所以最优阶次n的估计和重视其他阶次子序列等问题亟待解决[11-16]。

由于符号序列长度通常不相等并且数据之间有顺序关系，所以符号序列相似性度量成为难题。当前研究符号序列的主要方法主要有两种。

第一种是直接法。通过序列比对直接度量序列间相似性，如果满足相同的或者相似的符号子串越多相似性越大。代表性算法包括SCS、n-gram等。以n-gram算法中n=2为例，对aenhashow和aenheshowe进行分段，可得如下结果（采用斜体标出公共子串）：

ae，en，nh，ha，as，sh，ho，ow

ae，en，nh，he，es，sh，ho，ow，we

比对后发现两序列的公共符号子串数为6。但是直接法缺点是不能捕捉符号序列下有序符号的隐藏信息，譬如序列中全局结构信息等。

第二种是间接法。此法能够捕捉隐藏在序列中的全局结构，也称其是基于模型的方法。然而基于模型的方法劣势是度量两个序列间相似性时仅仅利用两个序列所构建的模型，而忽略了数据集整体的统计信息。

上面两种方法，即子序列法和概率模型法，用于提取序列结构特征。第一种以n-元组为代表，目的是提取蕴含在序列中的局部结构信息，后者通过Markov模型、隐Markov模型记录序列中的全局结构信息。我们可以理解n-元组是序列中n个连续符号构成的短子序列，相当于n-阶Markov模型中的前缀子序列。由此可以说，n-gram方法是Markov模型的一种应用[17]。当前，基于Markov模型的分类器已成为符号序列分类的主要工具之一[18-19]。

然而，当n给定后，仅有固定阶次的子序列进行序列分类，而忽略其他阶次子序列中的结构信息，必然影响符号序列Markov分类的性能。

本文针对上述问题，提出一种符号序列贝叶斯分类新方法，该方法是基于多阶Markov模型基础上的，高阶的Markov链表示马尔科夫链的高阶记忆性，即下一步的状态不仅和当前状态相关，同时和之前多步的状态也相关，这将有助于提高基于行为符号序列的银行客户破产风险的预测精度。首先开展对序列中各种符号以及符号彼此顺序关系的监督学习，预测对象的类别标号，提出多阶马尔科夫模型；然后在一个统一的模型中同时使用1~n阶马尔科夫链模型化符号序列，并构造新的算法，最终提出了一种新的贝叶斯分类器[20]。

2 相关工作

首先约定使用记号。W为训练数据集（由N个样本构成的），每个样本是一个二元组（S，k），其中S表示符号序列，k∈[1，K]是序列S的类别标示，K为类别数。序列S的长度记为L，即S表示为S=s1，s2，…sL。所有符号的集合记为D，|D|表示其中的符号数；因此，si∈D，i=1，2…L。

基于如下假设：任一序列S中符号si与其前缀子序列s0，s1…si-1相关性很大，其中s0表示序列的起点。采用n阶马尔科夫模型时，前缀子序列被截断为δl（n）=sl-n…sl-1，其中j＜0的符号sj用s0代替，所以n阶马尔科夫模型中的前缀子序列具有固定的长度n，用“（n）”标识。序列S的概率是条件概率的乘积来估计，即：

式（1）表示的模型称为符号序列的条件概率分布模型[13-16]。用于分类时，式中的条件概率根据训练数据集中符号的条件分布估计；显然，这种条件分布随训练类别的不同而有所差异。记符号sl相对于第k个训练类别的条件概率为，通常使用如下拉普拉斯校正估计：

其中，fk（t）表示子序列t在第k个训练类别的所有序列中出现的次数。

2.1 符号序列多阶马尔科夫模型

在一个n-阶Markov模型中，序列S中符号sl的条件概率定义在长度固定为n的前缀子序列δl（n）=sln…sl-1上。对于一个给定的序列集，理想的模型阶数可能是1，2，3…具体取值应与序列结构有关。鉴于估计最优模型阶数的困难，本文提出多阶模型方案，基于如下假设：（X）给定一个较大的n，序列集最优Markov模型的阶数i∈[1，n]；（Y）任何阶数为i∈[1，n]的模型都是可能的，但各模型的“可能性”不同。对于序列S中的符号sl，事实上，其n-阶Markov模型下的前缀子序列已经包含了所有i∈[1，n]阶前缀子序列。注意到是的后缀子序列，这为构造融合i∈[1，n]阶的多阶模型提供了基础。

结合上述假设，序列S第k类的先验概率P(S|k)估计为：

由式（3）可以分析得出包含n个条件概率，i∈[1，n]。衡量各阶次Markov模型的“可能性”，即不同阶次条件概率的贡献度，我们用“阶次权重”（简称“阶权”）w1-1，w2-1，…，wn-1表示。显然，若wn=1且其他i∈[1，n]阶的权重为0，式（3）退化为单阶条件概率模型。另一方面，从优化的角度看，当所有权重均为0时P（S|k）取最大值，为避免所有阶次模型具有相同的可能性，并区分不同阶次的贡献，务必对式（3）进一步约束，条件是：。

2.2 多阶马尔科夫模型算法的构造

通过遍历扫描序列集而获得的条件概率，既可以提高计算的效率，又能够使得算法更加高效。为得到式（3）中的多阶模型，所以为每一条序列的每一个符号sl计算条件概率pk（sl|δl（i）），我们称这种数据结构为“附后缀表的N阶后缀树”，简称n-STS，如图2所示。

如图2所示，序列“XYXXXYYXY”和“YYXYXYX”由‘X’和‘Y’两个符号组成，在每个结点上附加一个后缀表，用来记录当前结点对应子序列作为前缀的符号个数。其中以‘X’为后缀的3阶对应树上5条路径，分别是“□□X”“XXX”“YXX”“XYX”和“YYX”，假设，在序列“XYXXXYYXY”和“YYXYXYX”中，3-元前缀子序列“YYX”之后符号＇Y＇出现了2次，‘X’为0次，所以标注TXYY为图中格式。同理，子序列“YX”是“YYX”的后缀子序列，所以其结点是“YYX”对应的叶子结点的父结点，由此在“XYXXXYYXY”和“YYXYXYX”序列中，TXY的标注表示以“YX”为前缀，其后的‘X’和‘Y’的计数分别为1和3。

图2中的重要性质是：前缀子序列在序列集中的计数即是后缀表中所有计数的和。所以利用式（2）和n-STS树可得出每个符号的条件概率。譬如，对于2-元前缀子序列δl(2)=“YX”，由TXY可知fk(“YXX”)=1和fk(“YXY”)=3，则fk(“YX”)=fk(“YXX”)+fk(“YXY”)=4；由式（2）得出估计条件概率为pk(＇X＇|δl(2))=(1+1)/(4+2)≈0.33和pk(＇Y＇|δl(2))=(3+1)/(4+2)≈0.67。综上所述最终得到式（3）所需的所有阶次的条件概率。

初始模型阶数n和给定训练集W，可以为每个类k的序列构造一棵n-STS树，各个树根结点用NK表示，k=1，2…K；每棵树最多有|D|棵子树；算法扫描每条序列S，为其上每个符号sl提取其n-元前缀子序列δl（n），插入n-STS树后更新各个结点的后缀表。算法过程描述如下。

算法：n-STS树构造算法；

输入：训练集W，阶数n；

输出：K棵n-STS树。

算法扫描序列集一次构造出K棵n-STS树。算法的时间复杂度为O（n×M），其中，M表示W中所有序列的总长度。

2.3 改进后的贝叶斯分类器

OWYC即基于多阶Markov模型的符号序列贝叶斯分类器。给定训练集W以及由算法生成的K棵n-STS树，OWYC训练阶段算法从中学习优化的阶权集合W={wi|i=1，2…n}。采用最大似然学习法，最大化下列目标函数：

将其代入式（3）引入归一化约束条件式后使用拉格朗日乘子法λ，目标函数变为：

3 实验方法和步骤

分别在3个不同应用领域开展实验，形成6个数据集，包括银行客户行为序列、基因、语音序列（表1）。DNX序列集DS1和DS2、语音序列集YS1和YS2中序列长度较长，其中DNX取自NCYI基因库和PYIL微生物同源基因家族库。语音序列集由5个法语元音（＇X＇，＇e＇，＇i＇，＇o＇，＇u＇）的音频分箱取样而来。银行客户行为序列来自连续10或12个月信用卡交易行为符号序列，反映客服行为的符号数为3个。序列长度分别是10或12。相对DNX序列集序列长度较长，符号数也较多，语音序列集YS1和YS2的符号数是最多的。

3.1 实验数据与设置

实验采用4种不同方法形成分类器性能的对比，见表2，分别采用一阶马尔科夫模型的贝叶斯分类器为（简称为BC），BC分类器相当于OWBC一个特例：当wn固定为1且wi-1=0时，OWBC即可退化为BC。还采用1-NN（近邻数为1的近邻分类器）、SVM方法，二者都使用基于n-gram的符号序列向量表示模型。为提高分类性能，1-NN分类器采用加权投票法，SVM分类器为C-SVC，采用了LIBSVM的实现。使用分类精度CA作为各种分类器指标的评估。

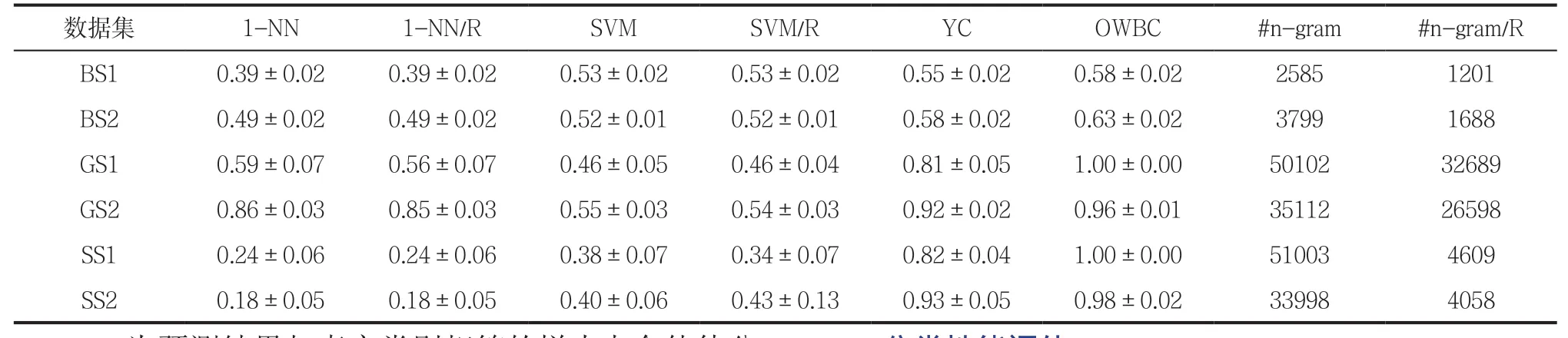
表2 实际序列集上不同分类器的平均分类精度及n-gram数目

CA为预测结果与真实类别相符的样本占全体待分类样本的比例，计算公式如下：

式（6）中I是取值0或1的指示函数，k＇S表示分类器预测的类别标号，kS表示测试序列S真实类别标号，|W|为测试序列的数量。由此可见，CA的值越大分类器具有越好的分类性能。

3.2 分类性能评估

表2数据显示，由于数据高维的特性以及高维空间特征间存在相关性，所以1-NN和SVM的平均分类精度明显低于两个贝叶斯分类器。还看出银行序列集经过特征约简后1-NN和SVM的平均分类精度基本保持不变；在基因序列和银行序列中GS1、GS2、BS1、BS2，SVM上的平均分类精度略有提高；但在SS1、SS2上精度显著下降。这说明固定阶数子序列如果进行特征简单的约简处理，其实不能有效提高分类精度。

由图3可以看出，不同阶次子序列对序列类别的预测会因为贡献程度不同导致预测结果不同。同时还发现一个有趣的现象：BS1，BS2的银行客户行为序列，GS1，GS2的DNA序列，都会随着阶次的提高对分类的贡献表现出增加的趋势，但是并不适用于SS1，SS2语音序列，而只有在3阶子序列时贡献最大。以上分析将为确定符号序列马尔科夫模型最优阶数提供参考。

3.3 预设阶数n的影响

由3.2节分析得出，OWBC算法时间复杂度为O（n×M），阶数n和序列总长度M呈线性关系，算法复杂度则是O（n2×M），接下来实验将重点关注算法复杂度。从图4不难发现，OWBC算法随着阶次（2＜=n＜=8）所需时间呈多项式增长趋势。因为实际应用中n＜＜M，所以OWBC学习效率较高。6个实际序列集上的训练任务均可在1秒内完成。

如图5所示，本组实验采用5-折交叉验证法，对于两个银行客户行为序列来说，OWBC平均分类精度在n＞6时略有下降。在两个DNA序列集上，其平均分类精度随n变大反而略有增加。但是在语音序列集上OWBC接近100%的高分类精度。可以说OWBC对预设阶数n的变化是鲁棒的。OWBC采用的多阶马尔科夫模型加权融合机制，既能够抵消不正确模型阶数对分类器性能的影响，又可以在不同应用领域序列集上取得高质量分类结果。

4 结语

目前广泛使用的支持向量机、决策树等机器学习方法多针对向量型数据，而符号序列Markov分类多数是基于固定阶Markov模型（n-阶Markov模型），而阶数n与所提取的序列结构特征息息相关，其值将直接影响分类器的性能。本文提出多阶马尔科夫模型，为构造多阶模型，提出了后缀树结构，并且构造出后缀树的高效算法，最终提出新的贝叶斯分类器。新分类器的训练算法既可以学习各种符号不同阶次的条件概率，还可以优化不同阶次的权重。为验证新分类器有效性，我们在三个实际应用领域的序列集上开展实验，并验证了新的分类器对预设阶数n是鲁棒的。新分类器通过使用多阶马尔科夫模型加权机制，可抵消错误模型阶数对分类器性能的影响，得出可在不同应用领域的实际序列集上取得高质量的分类结果。