基于非线性动力学的分数阶直驱式永磁同步发电机建模与性能分析

解 骞，李佳鑫，贾业萌，杨晓萍，郭 舵

(1.西安理工大学 电气工程学院，陕西 西安 710048；2.天津大学 建筑工程学院，天津 300072)

随着我国风力发电产业的迅速发展，直驱式永磁同步风力发电机(D-PMSG)在电网中占有的比例不断升高[1]。D-PMSG采用低速永磁发电机且风轮与电机直接耦合，这种发电机取消了风力机和发电机之间的增速齿轮箱，具有高效率、低噪声、高寿命等优点[2,3]。

当某些参数处于一定工作范围时，系统就会产生不稳定的运行状态，甚至混沌状态[4]，具体表现为产生不规则电磁噪声、转速和输出功率间歇性振动等现象[5]。目前，国内外已就D-PMSG开展了大量研究[6-8]，但是这些研究主要基于整数阶D-PMSG数学模型[9]。相较于整数阶系统，分数阶系统更易稳定，且可以更好地揭示和描述自然现象[10-12]，许多系统可以由分数阶微积分恰当地描述。因此，本文基于分数阶D-PMSG数学模型，研究其动力学行为，探究参数和阶数变化对系统运动状态的影响机制。

另一方面，在现有的研究中，大多数学者忽略了发电机与电动机的区别，在研究发电机时却使用了电动机的模型，并且采用的都是理论参数，而未采用实际的运行参数进行分析。因此，本文基于笔者先前的研究成果[13]，建立一个具有实际参数的30 kW分数阶D-PMSG模型，使得本文的研究内容更具实际意义。

1 分数阶微积分理论

在分数阶微积分理论的发展过程中，许多学者提出了多种不同的分数阶微积分定义，但是主要有Riemann-Liouville分数阶微积分定义以及Caputo分数阶微积分定义。

1)Riemann-Liouville分数阶导数定义式为：

(1)

式中：Γ(·)表示Gamma函数。

当给定的函数x(t)=(t-α)β，函数(t-α)β可积，且β>-1时，由Riemann-Liouville给出的分数阶导数的定义为：

(2)

这里限制x(t)=(t-α)β，β>-1且此函数具有可积分性。

2)Caputo分数阶导数定义式为：

(3)

其中，xm(τ)为函数x(τ)的m阶导数，m-1≤q≤m+1，m为整数。

2 分数阶D-PMSG数学模型建立

对于D-PMSG，通常采用d-q转子坐标系，由此可以得到D-PMSG的空间矢量图，如图1所示。

从而得到电压方程、磁链方程、转矩方程以及运动方程：

1)电压方程：

(4)

2)磁链方程：

(5)

3)转矩方程：

(6)

4)运动方程：

(7)

由此，D-PMSG模型可以表示为：

(8)

式(8)中参数的含义，如表1所示。

表1 D-PMSG数学模型参数Tab.1 Mathematical model parameters of D-PMSG

本文采用表贴式结构的D-PMSG，根据其特性可知Ld=Lq。

从式(8)可以看出，D-PMSG系统代表高度非线性系统，在动态分析过程中将会变得非常复杂。因此，采用仿射变换对式(8)所示的模型进行简化。简单来讲，仿射变换就是“线性变换”加“平移”。一组平行直线经过仿射变换之后依然是直线，且直线的比例保持不变[14]。由于其特有的性质，仿射变换在非线性动力学分析中有着重要作用。

下面考虑仿射变换的形式：

(9)

由此，可以得到以下两种变换：

(10)

(11)

定理1[13]：对于一个三维动态系统：

(12)

定义：

将已知条件代入式(8)，可以得到：

(13)

利用式(10)、式(11)以及定理1，可得简化后的数学模型：

(14)

其中：

(15)

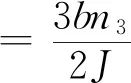
(16)

(17)

(18)

(19)

(20)

由此可以得到分数阶D-PMSG的数学模型：

(21)

D-PMSG的风力发电机组主要由风力机和D-PMSG两部分组成，风力机将风能转化为机械能，带动D-PMSG转子旋转，从而产生电能。D-PMSG的基本框图如图2所示。

图2 D-PMSG的基本框图Fig.2 Basic block diagram of D-PMSG

3 分数阶D-PMSG非线性动力学及性能分析

分数阶D-PMSG数学模型为非线性系统，具有复杂的动力学行为。然而当D-PMSG的参数发生变化时，可能会出现一些不稳定运动状态，这将严重影响其工作稳定性，降低甚至破坏发电机的性能，限制众多机电设备的工作范围。非线性分析方法是研究系统动力学行为最重要的方法。下面将在不同情况下对系统进行数值仿真，并分析其动力学行为。

3.1 当参数ϑ变化时

取一组参数μ=3、ψf=2.5，初始参数选择为[0.1，0.1，0.1]，分岔参数ϑ∈(0,35)。

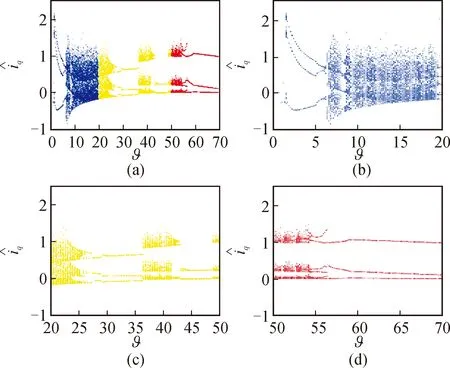
图3 q1=q2=q3=1.03时与ϑ的分岔图Fig.3 Bifurcation diagrams of versus ϑ,q1=q2=q3=1.03

从图3(a)中可以看出，随着ϑ的变化，系统在大多数情况下为混沌状态。当参数逐渐增加时，系统最终通过一系列分岔行为摆脱混沌状态。

图3(b)～(d)描绘了分岔图(图3(a))中更多的动力学行为细节。图3(b)描述了图3(a)中参数ϑ∈[0,20]区间上的分岔图，图中发现了霍普分岔。当ϑ=1.5时，系统开始失去稳定状态，发电机运行性能也开始降低。在ϑ∈(1.5,6.6)范围内，系统有三个周期。当分岔参数ϑ=6.6时，系统出现了倍周期分岔，由周期运动进入了混沌状态。之后在混沌区中，出现了两个周期窗口，此时发电机会产生剧烈振荡、机组过热等现象，使系统无法正常工作，甚至造成损坏。

图3(c)描述了图3(a)中参数ϑ∈[20,50]区间上的分岔图，能够观察到两个明显的周期窗口。在这里可以观察到逆分岔、吸引子合并激变和内部激变：当ϑ=25.27和ϑ=42.72时发生逆分岔；在ϑ=38附近，系统会出现合并激变和内部激变。

图3(d)描述了图3(a)中参数ϑ∈[50,70]区间上的分岔，系统在该区间内大多为周期运动。随着分岔参数ϑ的增大，在经历了一个短的混沌区之后，当ϑ>42.72时，系统开始摆脱混沌状态，进入周期运动。

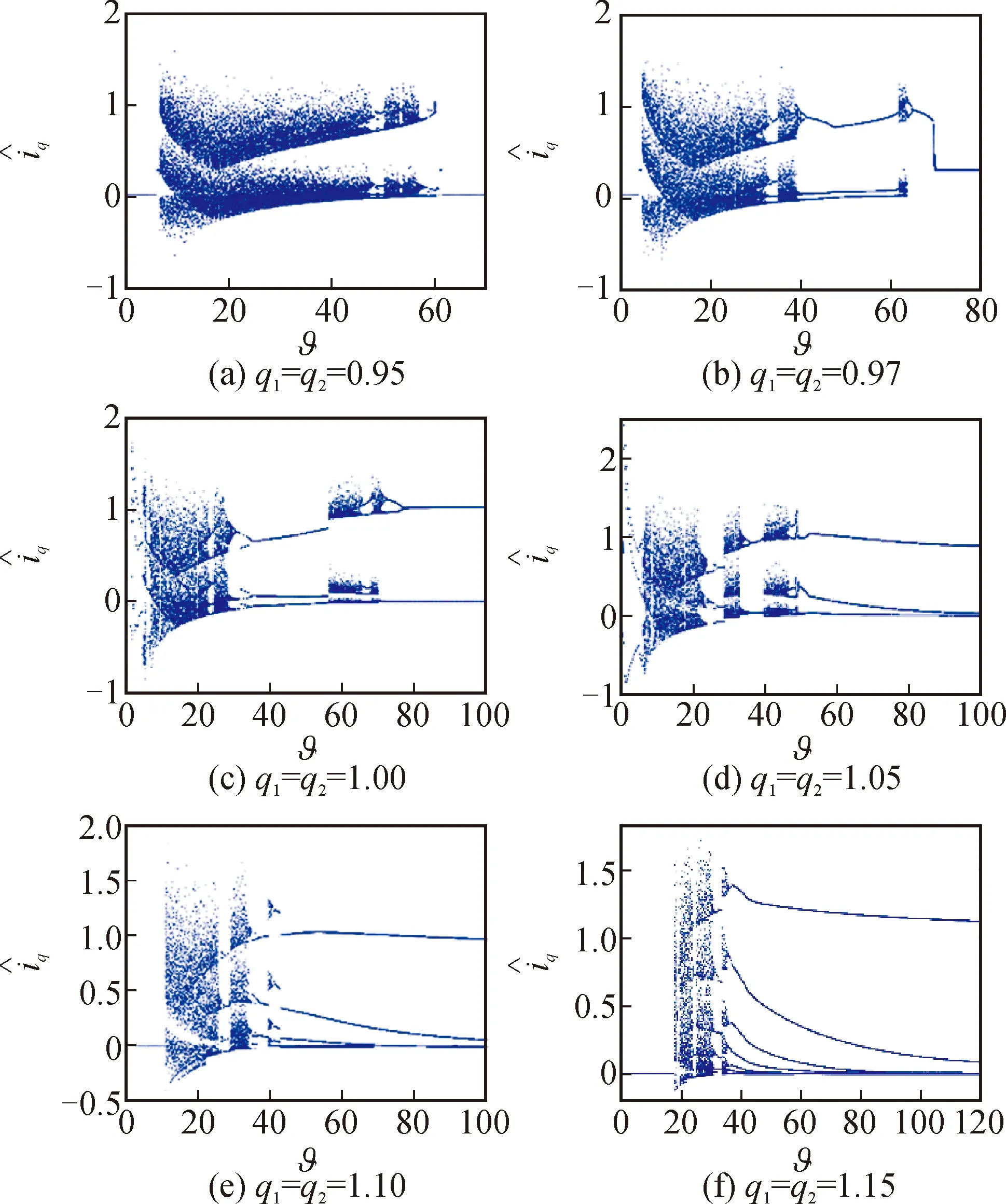
图4 系统阶数q3=1.03、q1与q2变化时，与ϑ的分岔图Fig.4 Bifurcation diagrams of versus ϑ with different system orders (q1,q2)and q3=1.03

比较这些分岔图可以发现，不同阶数的系统都经历了分岔和周期窗口。另一方面，系统的阶数确实能对系统的混沌以及分岔行为产生影响。

当q1=q2=0.95，q3=1.03时，系统的分岔图如图4(a)所示。随着分岔参数ϑ的增大，当ϑ=6.62时，系统突然变得混沌。然后，系统在一个大范围内保持混沌状态。当ϑ=47.13时，出现了一个明显的周期窗口。直到ϑ=56.96，系统保持稳定。

与图4(a)相比，图4(b)中多了一个大的周期窗口。随着分岔参数ϑ的增大，当ϑ=3.75时，系统突然变得混沌，在ϑ∈(35.52,39.06)范围内，存在一个短的混沌区，之后经历一个大的周期窗口和一个短的混沌区后，系统再次保持稳定。

在图4(c)中，同样有一个很大的周期窗口。随着分岔参数ϑ的增大，当ϑ=2.00时，系统突然变得混沌。此外，还可以明显观察到，在ϑ=30和ϑ=70附近，系统出现逆分岔。

在图4(d)～(f)中，系统经历了混沌和许多小的周期窗口，最终通过一系列的分岔行为摆脱混沌。

当ϑ=29.2时，在图5中绘制了具有不同系统阶数的iq-id相图，从不同的角度描述了系统的动力学行为，与系统分岔图相对应。

图5 系统参数ϑ=29.2，阶数q3=1.03、q1与q2变化时的相图 phase graphs with different system orders(q1,q2)and q3=1.03,ϑ=29.2

此时，随着阶数的增加，相图中一直呈现出混沌吸引子，表明系统处于混沌状态。这时，发电机出现剧烈振荡，不能正常运行，并且还会影响周边设备的正常运行。从图中可以看出，当系统阶数增加时，吸引子不仅改变了大小，而且改变了形状。例如，图5(f)中的吸引子比其他吸引子大，并且形状也与其他吸引子大不相同。

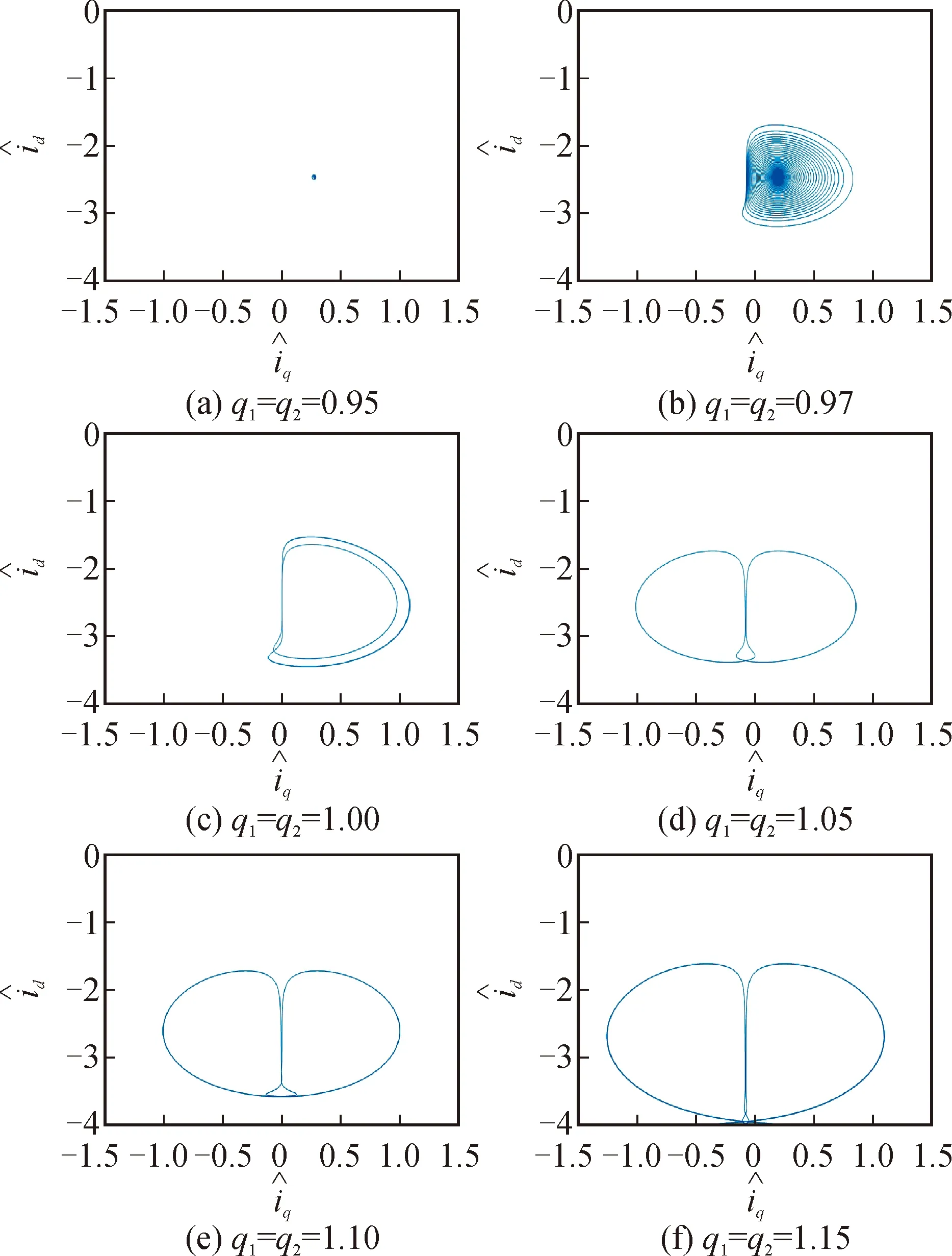
图6 系统参数ϑ=75，阶数q3=1.03、q1与q2变化时的相图 phase graphs with different system orders (q1,q2)andq3=1.03,ϑ=75

图5和图6中相图对应的功率谱密度(PSD)图分别示于图7和图8中，其与分析结果一致。

图7 系统参数ϑ=29.2，阶数q3=1.03、q1与q2变化时的功率谱图Fig.7 PSD diagrams with different system orders (q1,q2)andq3=1.03,ϑ=29.2

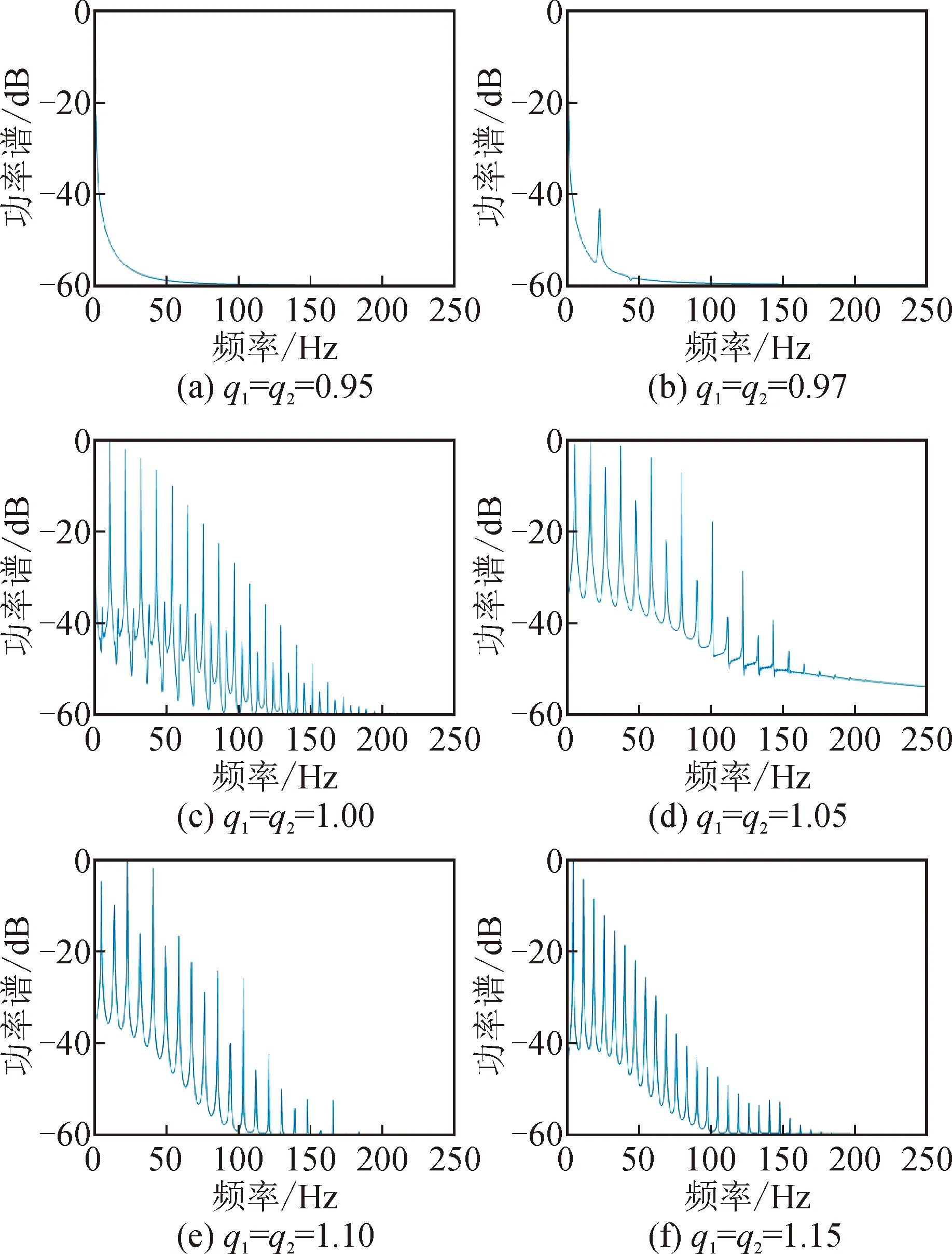
图8 系统参数ϑ=75，阶数q3=1.03、q1与q2变化时的功率谱图Fig.8 PSD diagrams with different system orders (q1,q2)andq3=1.03,ϑ=75

分析所有的分岔图可以发现，当参数ϑ变化时，总能找到一个区间范围，使得系统处于稳定状态。这为发电机的设计提供了理论上的帮助。例如，当q1=q2=q3=1.03时，系统在ϑ∈(0,1.5)范围内是稳定的。结合式(16)，只要在设计时选取合适的黏性阻尼系数b、转动惯量J，就可以使发电机稳定运行，保持较好的性能。

图9给出了ϑe与系统阶数q之间的关系。ϑe表示混沌结束时的ϑ，q表示q1、q2，其中q1=q2。从图中可以看出，ϑe与系统阶数q之间的关系比较复杂。当q从0.95增加到1时，ϑe逐渐增大；但当q继续从1增加到1.15时，ϑe开始减小，特别是在q∈[1,1.05]范围内，ϑe下降较快。

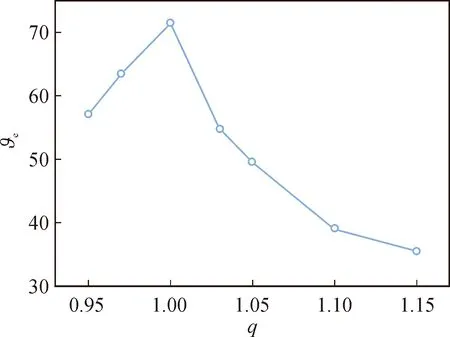
图9 ϑe与系统阶数q之间的关系Fig.9 ϑe versus system order q

3.2 当参数μ变化时

取一组参数ϑ=9.8、ψf=4.2，初始参数选择为[0.1,0.1,0.1]，分岔参数μ∈(0,4)。

图10(b)描述了图10(a)中参数μ∈[0,1.5]区间上的分岔图。当分岔参数μ=0.36时，系统开始失去稳定，当分岔参数μ=0.56时，系统突然进入混沌，之后一直处于混沌状态。当系统处于混沌状态时，发电机会出现剧烈振荡，不能正常工作，严重时甚至损坏电机，产生事故。

图10(c)描述了图10(a)中参数μ∈[1.5,2.4]区间上的分岔图，在图中出现了一个周期窗口。从μ=1.5开始，系统处于混沌状态，之后经历分岔，当μ=2.05时，系统再次进入混沌状态。在该图中，可以发现吸引子内部激变和合并激变。

图10(d)描述了图10(a)中参数μ∈[2.4,4]区间上的分岔图。图中可以观察到明显的分岔行为，当μ=2.55时，发生逆分岔，当μ=3.32时，系统再次达到稳定状态。

图10 q1=q2=q3=1.03时与μ的分岔图Fig.10 Bifurcation diagrams of versus μ,q1=q2=q3=1.03

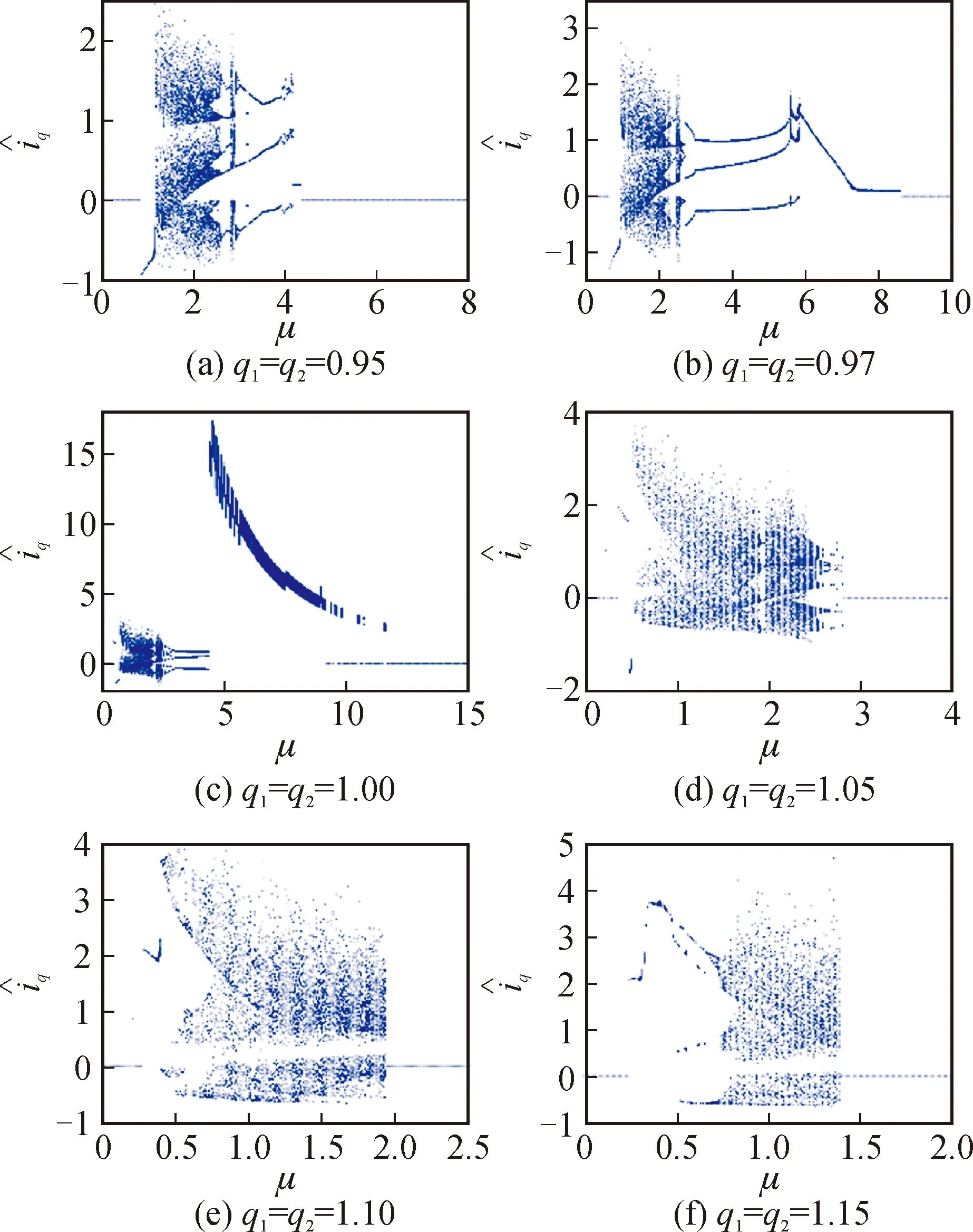
图11 系统阶数q3=1.03、q1与q2变化时，与μ的分岔图Fig.11 Bifurcation diagrams of versus μ with different system orders (q1,q2)andq3=1.03

从图11(a)～(f)中可以看出，当μ到达一定值时，系统会突然进入混沌，这在系统阶数q1、q2不同时表现得有所不同。虽然系统的阶数有所不同，但是系统在经历了一系列分岔、混沌之后，最终都回到稳定状态，并且在图11(a)～(c)中都出现了吸引子内部激变和合并激变，而在图11(f)中存在霍普分岔。

图12 系统参数μ=1，阶数q3=1.03、q1与q2变化时的相图 phase graphs with different system orders (q1,q2)andq3=1.03,μ=1

图13 系统参数μ=0.6，阶数q3=1.03、q1与q2变化时的相图 phase graphs with different system orders (q1,q2)andq3=1.03,μ=0.6

图12和图13对应的PSD图如图14和图15所示，与分析结果一致。

图14 系统参数μ=1，阶数q3=1.03、q1与q2变化时的功率谱图Fig.14 PSD diagrams with different system orders (q1,q2)andq3=1.03,μ=1

图15 系统参数μ=0.6，阶数q3=1.03、q1与q2变化时的功率谱图Fig.15 PSD diagrams with different system orders (q1,q2)andq3=1.03,μ=0.6

分析所有的分岔图可以发现，当参数μ变化时，总能找到一个区间范围，使得系统处于稳定状态。这为发电机的设计提供了理论上的帮助。例如，当q1=q2=q3=1.03时，系统在μ∈(0,0.36)及μ>3.2范围内是稳定的。结合式(15)，只要在设计时选取合适的极对数np、黏性阻尼系数b和定子绕组电阻R，就可以使发电机稳定运行，保持较好的性能。

图16给出了μe与系统阶数q之间的关系。μe表示混沌结束时的μ，q表示q1、q2，其中q1=q2。从图16中可以看出，μe与系统阶数q之间的关系比较复杂。当q从0.95增加到1时，μe逐渐增大，但当q增加到1之后，μe突然减小；当q∈[1.03,1.05]时，μe缓慢增大，但当q∈(1.05,1.15]时，μe依然随着q的增加而减小。

图16 μe与系统阶数q之间的关系Fig.16 μe versus system order q

3.3 当参数μ、ϑ、ψf固定，系统阶数变化时

取一组参数μ=0.6、ϑ=6.377 6、ψf=3，初始参数选择为[0.1，0.1，0.1]。

图17 系统参数μ=0.6、ϑ=6.377 6、ψf=3，阶数q1、q2与q3变化时的相图 phase graphs with different system orders (q1,q2,q3)and μ=0.6,ϑ=6.377 6,ψf=3

从图17(a)～(d)中可以看出，当系统阶数为0.95、0.97、1.10和1.05时，随着阶数的增加，相图中一直呈现出规则的圆，并不断向中心运动，表明系统可以运行到稳定状态。此时发电机运行性能良好，输出电压幅值和频率都较为稳定。但当系统阶数增加到q1=q2=q3=1.10及q1=q2=q3=1.15时，相图中呈现出混沌吸引子，如图17(e)、(f)，表明系统处于混沌状态。此时发电机不能正常运行，会出现剧烈振荡。

图17中相图对应的PSD图示于图18中，与分析结果一致。

图18 系统参数μ=0.6、ϑ=6.377 6、ψf=3，阶数q1、q2与q3变化时的功率谱图Fig.18 PSD diagrams with different system orders (q1,q2,q3)and μ=0.6,ϑ=6.377 6,ψf=3

4 结 论

本文根据一个实际的D-PMSG模型，采用仿射变换的方法，建立了分数阶D-PMSG新的紧凑方程式(21)，并且通过非线性动力学理论以及分数阶理论，分析了分数阶D-PMSG系统中不同参数、不同系统阶数变化时的影响。

由本文分析可知：第一，在不同系统阶数下，D-PMSG会有不同的动力学行为，系统的运动状态也会随之改变；第二，混沌吸引子的形状和大小也都会随分岔参数ϑ和μ的变化而变化；第三，在参数μ变化，阶数q1=q2=q3=1.03时，系统较其他阶数具有较大的稳定区间：ϑ=9.8，ψf=4.2时，系统在0<μ<0.36和μ>3.2范围内是稳定的；第四，结合本文对分数阶系统动力学行为的分析，相较于笔者先前对整数阶系统的研究，可以发现分数阶系统在单参数变化、阶数q1=q2=q3=1.03时，系统的稳定区间更大，使得满足发电机稳定运行时可供选择的系统参数范围更广；且当系统参数固定时，随着阶数的增加，系统逐渐进入混沌状态；第五，得到发电机稳定运行的区间，在发电机设计时，可以选取合适的实际参数，保证发电机获得更可靠、更良好的性能；第六，得到参数ϑ和μ变化时，系统脱离混沌时相应的系统参数与阶数q之间的关系曲线，这对在其他阶数下获得系统的稳定区间具有重要意义。

本研究中采用的实际D-PMSG参数、建立的数学模型，相较于其他研究更具有实际意义。此外，本文的研究对进一步探索D-PMSG及其他分数阶系统的动力学特性具有一定的参考价值。