兰州高能电子成像实验平台电子束团长度测量研究

艾 蕾，赵全堂，宗 阳，冉朝晖，袁肖肖，曹树春,3，李 佳,3，申晓康,3，赵书俊，张子民,3

(1.郑州大学 物理学院，河南 郑州 450000；2.中国科学院 近代物理研究所，甘肃 兰州 730000；3.中国科学院大学 核科学与技术学院，北京 100049)

高能电子成像(HEER)技术[1-6]是高能量密度物质(HEDM)[7-8]诊断的潜在方法之一，而HEDM的研究对天体物理学、等离子体物理学和加速器物理学具有重要的推动作用，因此中国科学院近代物理研究所搭建了一个专用于HEER的实验平台[9-10]。该平台已于2019年初完成基本安装调试，2020年平台已能开展成像实验，其成像空间分辨率可达1 μm[11]。通过优化束流品质提高成像性能，其关键在于束流参数的诊断，其中最重要的参数之一是电子束团长度。为了测量电子束团长度、重建电子束团纵向分布，本文搭建一个基于相干渡越辐射测量电子束团长度的实验平台。

1 实验平台

HEER实验平台的布局如图1[9]所示，其主要包括光阴极微波电子枪、热阴极微波电子枪、阿尔法磁铁、3 m长的行波加速管和实验终端。目前，实验平台只安装了热阴极微波电子枪，电子束团长度正是基于热阴极微波电子枪的电子直线加速器进行测量。由于热阴极微波电子枪产生的电子束团能散较大、长度较长而不能直接进入加速管，故利用阿尔法磁铁调节电子束团能散和长度，进而提升束流品质，其中电子束团长度及纵向分布测量是优化电子束团在阿尔法磁铁中传输的重要检测手段。直线加速器设计参数列于表1[11]，电子束团长度测量平台位于HEER实验终端前。

微波电子枪的工作频率为2 856 MHz，电子枪的射频电场用于对电子束团加速。电子束团从电子枪发射被输送到阿尔法磁铁中，通过调节磁场梯度和刮束器在磁铁中的位置优化电子束流品质。电子束团长度的测量方法包括时域法和频域法。时域法直接从电子或其辐射波的时间分布测量电子束团长度，包括条纹相机法[12]、电光采样法[13]、零相位法[14]和横向偏转法[15]。频域法从电子束产生的辐射能谱中测出电子束团长度，根据辐射产生机制的不同其可分为相干衍射辐射[16]、相干渡越辐射[17]、相干同步辐射[18]和相干Smith-Purcell辐射[19]。两种方法均能满足本研究对时间分辨率的要求，但结合实验室空间大小、实验简易程度及经费情况，最终选择频域法中的相干渡越辐射方法进行电子束团长度测量。

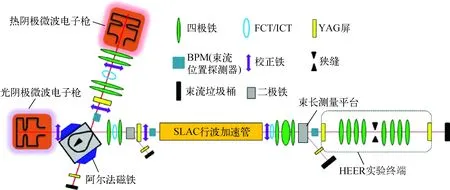
图1 HEER实验平台布局Fig.1 Layout of HEER platform

表1 直线加速器设计参数Table 1 Design parameter of linac

2 实验原理与方法

2.1 单个带电粒子的渡越辐射

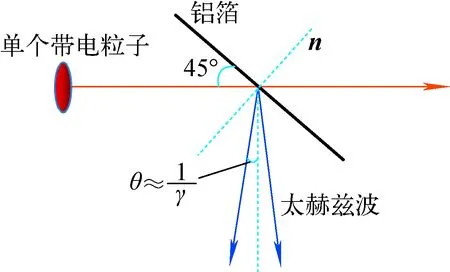
图2 渡越辐射原理图Fig.2 Schematic diagram of transition radiation

当带电粒子穿过两种介电常数不同的介质(如空气和铝箔之间的界面)时，会产生渡越辐射[20-21]。图2为单个带电粒子直线运动情况下的渡越辐射原理图，其中θ为观测角，γ为洛伦兹因子，n为法向量。将铝箔界面与电子束流入射方向呈45°角安装，可使后向辐射两边的辐射强度平均分布。生成的后向渡越辐射主要分布在与法向量相差45°角的左右两边，辐射波呈90°角离开真空室，其能谱空间分布可用Ginzburg-Frank方程[22]描述：

(1)

其中：Isp为单个带电粒子的渡越辐射强度；ω为太赫兹波的角频率；Ω为渡越辐射的立体角分布；e为电子电荷量；ε0为真空中的介电常数；c为真空中的光速；β为束流的相对速度。式(1)仅在远场大屏条件下有效且当θ满足式(2)时，Isp有最大值。其中γ≫1，故Isp只集中在1个很小的锥角内。

(2)

2.2 电子束的相干渡越辐射

电子束团产生的辐射强度必须考虑束团中每个电子的辐射强度，这与电子束团长度有关。当电子束团长度大于辐射波长时，电子辐射相位相差参差不齐，每个电子的辐射不相干，总辐射强度与电子束团中电子的个数呈正比。当电子束团长度小于或等于辐射波长时，电子辐射相位大致相同，辐射波满足相干条件，此时总辐射强度正比于电子个数的平方，其中电子束团渡越辐射[23]能谱为：

(3)

其中：N为电子个数；I为电子束团渡越辐射的强度；F(ω)为电子束团的形状因子，描述电子束团辐射的相干程度，定义为电子束团纵向密度分布的傅里叶变换的平方。

(4)

其中：k为电子束团波数；ρl(z)为电子束团的归一化纵向密度分布；Sl(ω)为电子束团纵向密度分布的傅里叶变换。由于电子束团中电子数在108～109数量级，对于短脉冲束，非相干辐射可忽略，因此式(1)可近似为式(5)，其中F(ω)可由单电子辐射和电子束团辐射能谱反推出来。

(5)

3 实验测量

3.1 实验装置

搭建的电子束团长度测量平台如图3所示。当超短脉冲电子束(束长在ps量级或以下)撞击铝箔时，产生的后向太赫兹波首先穿过用于真空密封的太赫兹窗。该太赫兹窗的材料是聚甲基戊烯(TPX)，厚度为3.5 mm，在频率为10 THz以下的透射率稳定在70%。穿过太赫兹窗的辐射波被离轴抛面镜(THORLABS，MPD269-F01)收集并传输到迈克尔逊干涉仪[24]中。迈克尔逊干涉仪(图3中虚线部分)由分光片(透射率约为54%，反射率约为46%)、定镜和动镜组成。入射光被分光片分成两部分，这两束光分别被定镜和动镜反射回分光片发生干涉，最后由高莱探测器(DYTEX，GC-1D)收集测量干涉能谱。

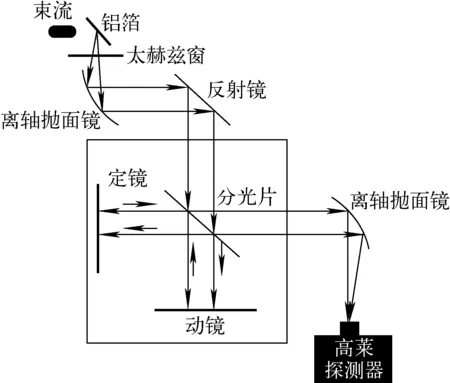
图3 电子束团长度测量平台Fig.3 Electron bunch length measurement platform

3.2 电子束团长度测量及纵向分布重建

1) 自相关曲线拟合

由于光学传输系统和探测器尺寸的限制，大部分低频辐射能量没有被探测器收集，整个探测系统可简化为高通滤波器。由于数据处理能力的限制，趋于无穷大的高频辐射能量需在最大有效信息处截断[25]，引入滤波函数g(ω)为：

g(ω)=1-e-ξ2ω2

(6)

其中，1/ξ为截止频率。

滤波函数表达形式来源于横向高斯光束衍射远场分布。低频辐射经衍射衰减后，到达分光片的电场强度Ef(ω)可表示为发射电场E(ω)与滤波函数g(ω)的乘积，即：

Ef(ω)=E(ω)g(ω)

(7)

其功率谱Pf(ω)为：

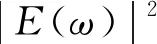
(8)

假设电子束团纵向分布为高斯分布，经过傅里叶变换、考虑辐射经过传输和探测光路衍射后，自相干曲线表达式[26]为：

(9)

其中：σ为均方根电子束团长度；τ为太赫兹波的干涉持续时间；τ0为干涉强度最大处的时刻。由于从强相干到弱相干的全过程，自相干能谱的测量数据与高斯分布类似，故式(9)可用于测量能谱拟合得出电子束团长度。

2) K-K相位分析法

任意线性无源系统的响应函数的实部和虚部之间存在K-K关系[27]，相位信息可通过形状因子的振幅得到，该方法称为K-K相位重建方法[28]。式(4)中Sl(ω)可为：

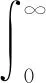
(10)

其中：ρ(ω)为形状因子振幅；Ψ(ω)为形状因子的相位。振幅和相位的K-K关系为：

lnSl(ω)=lnρ(ω)+iΨ(ω)

(11)

则最小相位因子Ψm(ω)可通过积分得到:

(12)

将式(12)代入式(10)后积分得到电子束团的纵向分布为：

(13)

为了验证K-K相位重建方法的可行性，本文进行了模拟数据验证，重建过程及结果如图4所示。由于文献[10]中在该加速管出口处模拟的电子束团分布为强度较大束流在前、强度较弱束流在后的密度分布，同时为了验证K-K方法的镜像特性，本文选择先弱后强的双高斯束流分布进行重建。图4a为随机设定均方根束长σ=0.06 ps的归一化模拟双高斯信号，即：

(14)

图4d为重建后经过镜像翻转处理的分布，该分布与原分布相同，证明K-K相位分析法是可行的。

3.3 两种方法的比较

自相关曲线拟合法可直接得出电子束团长度，但不能重建束团形状。而K-K相位分析法可从振幅推出相位信息，最后经过傅里叶反变换重建束团形状，得到束团纵向分布，但此方法的缺点为：对于非对称的双高斯束团，当强度较大的高斯分布在前面时，重建出的电子束团分布和真实分布完全一致。当强度较大的高斯分布在后面时，重建出的电子束团和真实束团的镜向一致，即头尾互换，这主要是因为电子束团和其镜向电子束团的傅里叶变换满足共轭关系，具有完全相同的模，仅是相位符号相反，而探测器无法感知二者的区别。因此利用K-K关系重建出的束团形状并不是唯一的，需要借助其他诊断方法来确定真实的束团形状是重建的还是其对应的镜向分布。

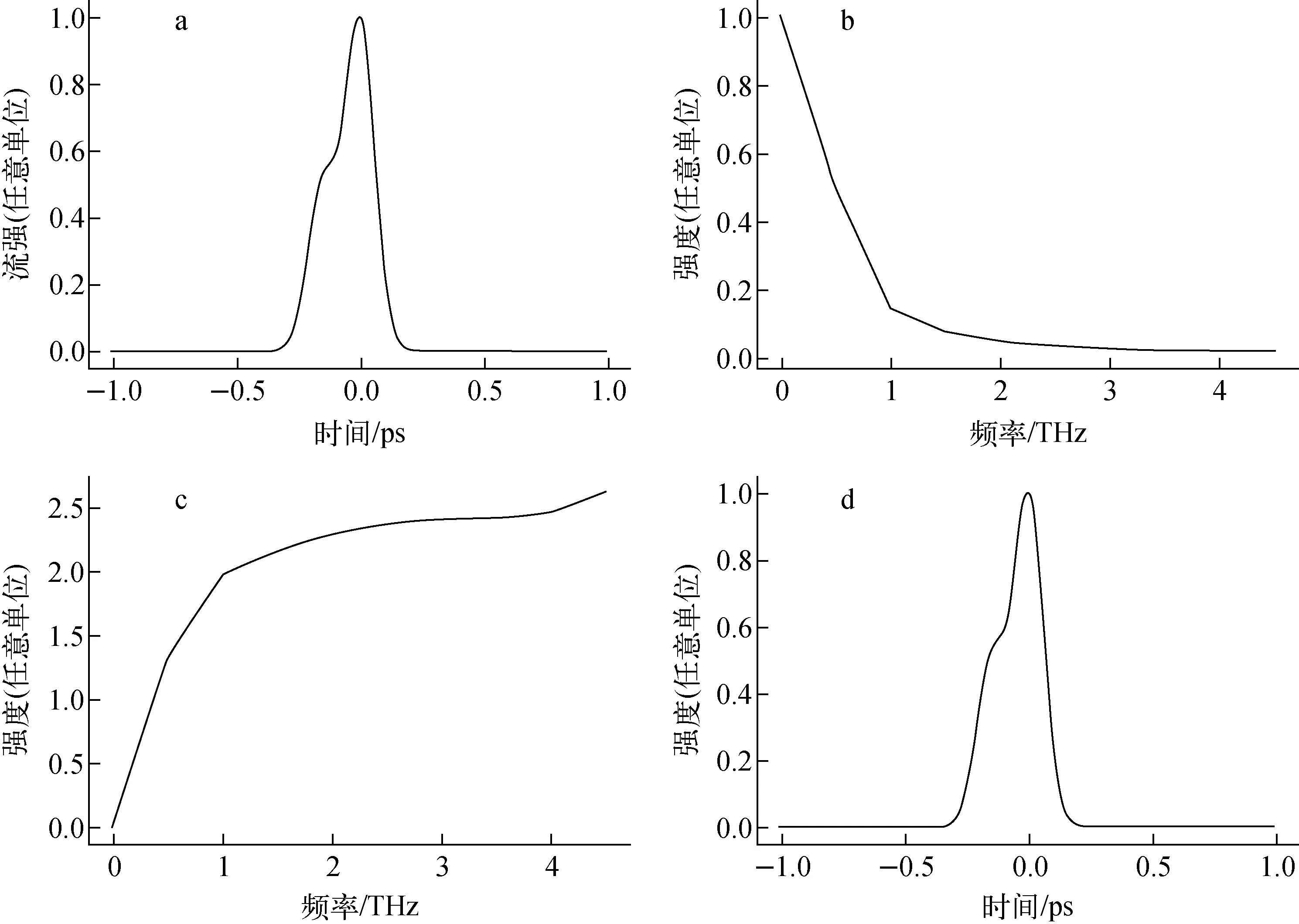
a——模拟信号；b——形状因子；c——相位因子；d——重建结果图4 K-K相位分析模拟实验Fig.4 Simulated test of K-K phase analysis

4 实验步骤及结果分析

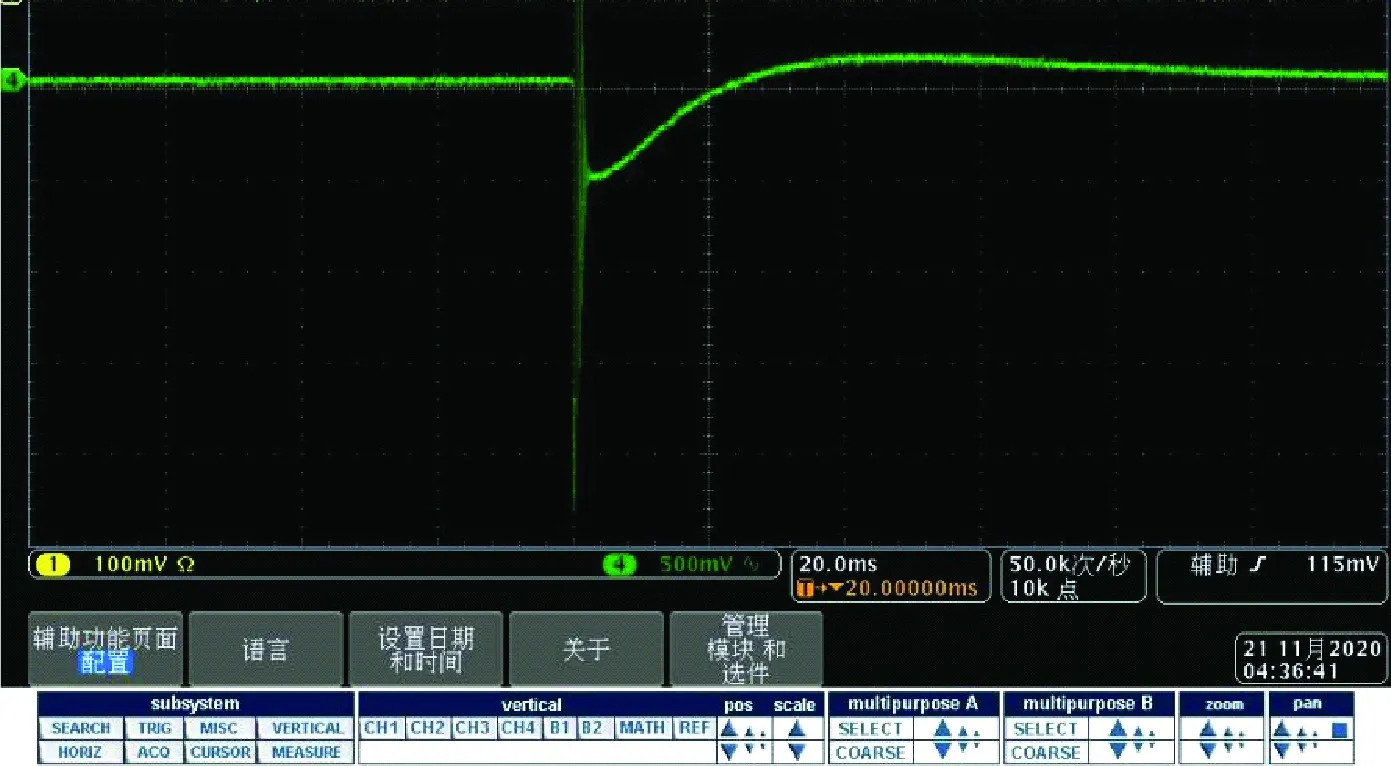
图5 示波器输出信号Fig.5 Signal of oscilloscope output

实验过程中，高莱探测器连接一台可远程调节的示波器(RTB2004-Digital oscilloscope-2.5 GSa/s)，干涉强度越大输出的电压越大。由于探测器需匹配2 000 Ω以上的电阻，该示波器只有50 Ω，因此输出信号产生一些畸变，但这种畸变不影响电压峰值的结果，图5为示波器输出信号。

控制动镜的步进电机(THORLABS，LST150/M)的精度为0.1 μm，行程为150 mm，设置步长为10 μm，在动镜每个位置测量5次干涉强度，进行统计分析。图6为束流宏脉冲峰值流强约为24 mA(由快速电流互感器测出)，即电荷量约为15 pC时的原始自相干曲线数据，微束团电荷量根据宏脉冲宽度及微脉冲频率估算出。5个样本测量前后的电流基本不变，可见束流流强稳定性较好。

图7为实验数据归一化后与理论函数的拟合结果，实验误差主要来自数据读取过程及动镜移动的位置误差。根据拟合结果，得出束团均方根长度约为0.723 5 ps，与束团电荷量为15 pC的直线加速器束流模拟结果基本一致。

图8为利用K-K方法重建出的一种可能的束团纵向分布，该分布的束团长度与自相关曲线拟合得出的束团长度基本一致，但形状呈不规则分布，束团末端的拖尾是导致束团能散较大的主要原因，这表明阿尔法磁铁还需进一步优化调试。

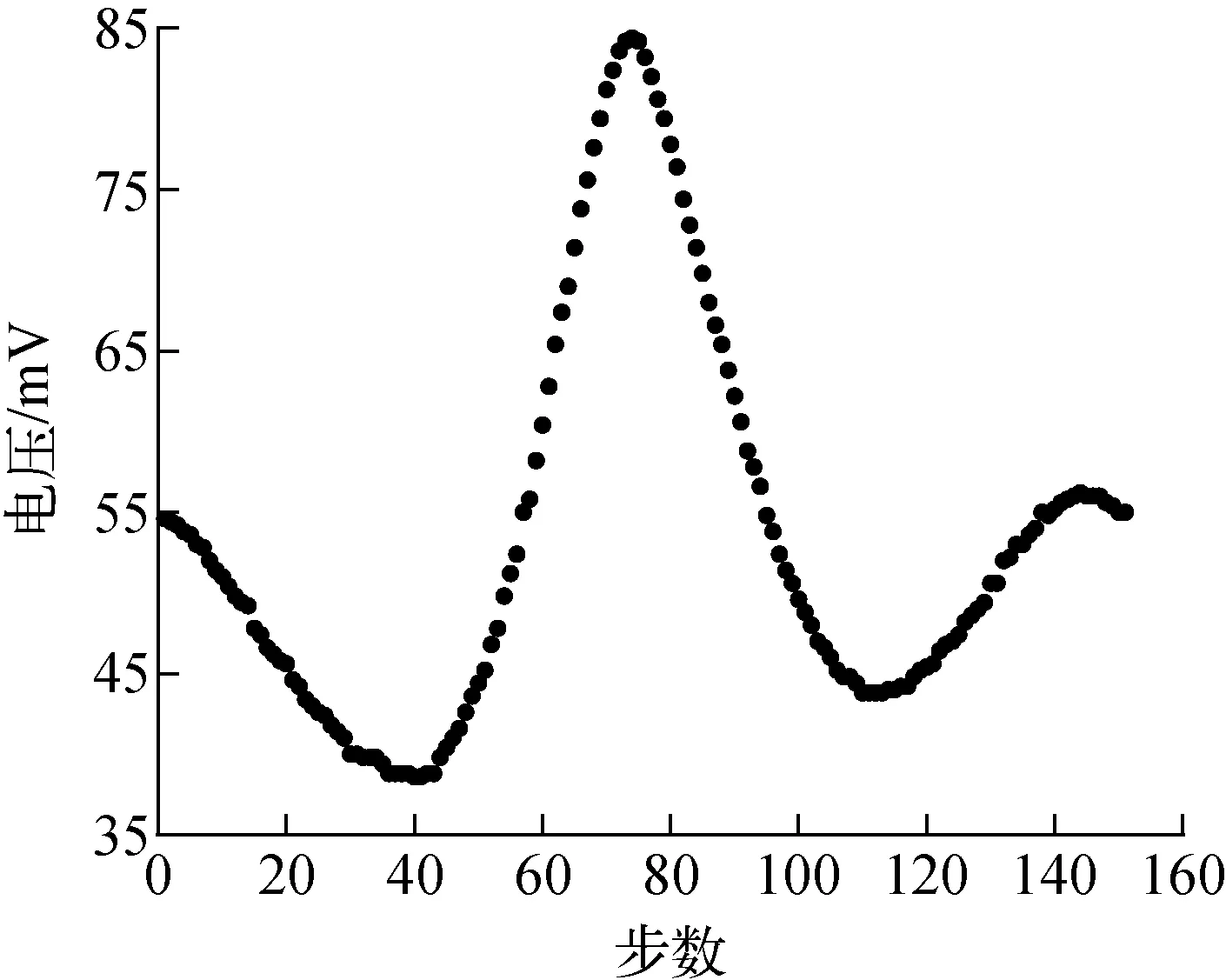
图6 自相干曲线数据Fig.6 Data of auto-coherence curve

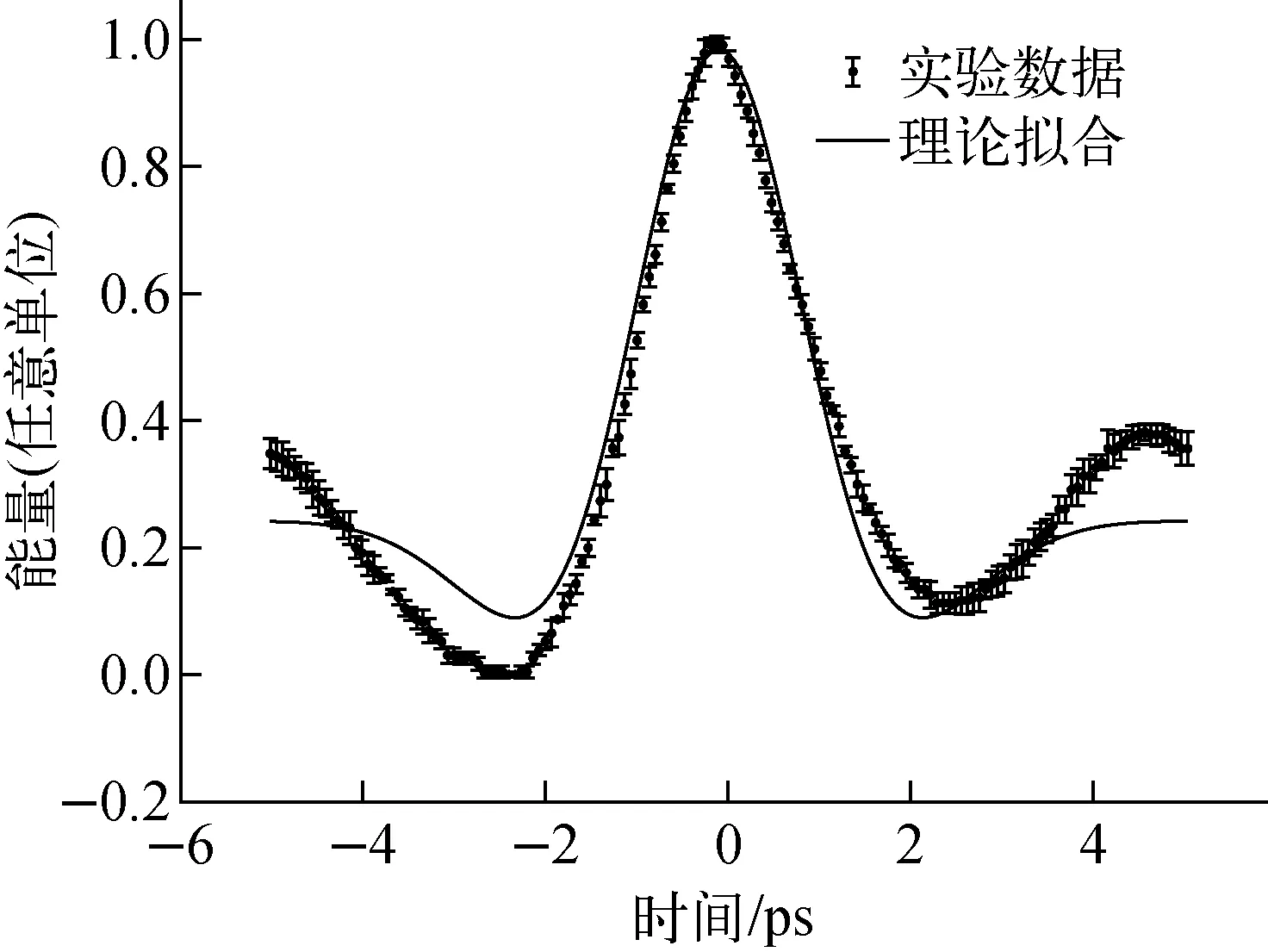
图7 自相干曲线的实验数据与理论函数的拟合Fig.7 Experimental data and theoretical fitting of auto-coherence curve

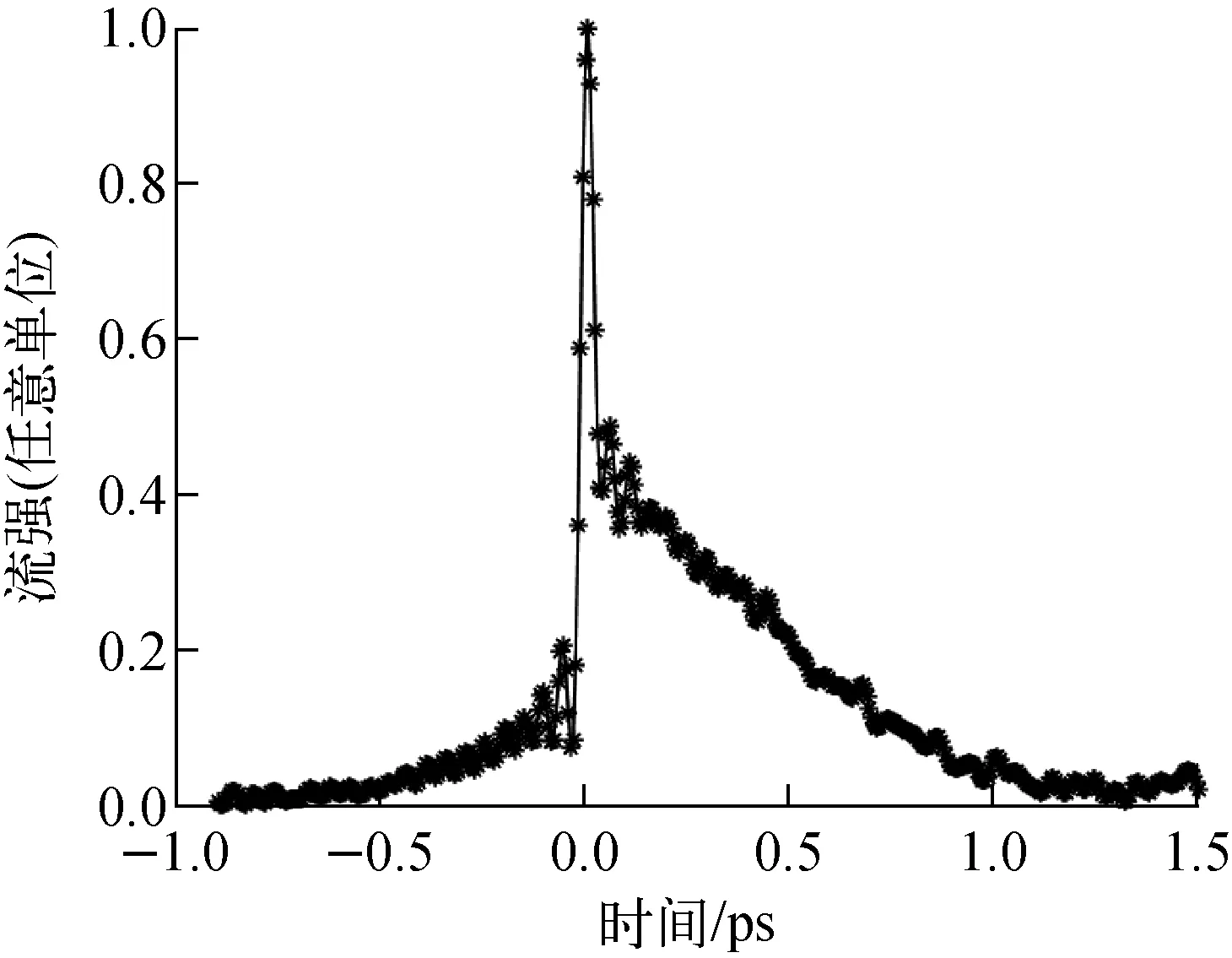
图8 K-K方法重建出的一种可能的束团纵向分布Fig.8 Possible bunch longitudinal distribution reconstructed by K-K method

5 结论

本文基于相干渡越辐射的能谱分析方法，利用自相关曲线拟合法得出HEER实验平台的直线加速器的电子束团长度，并用K-K方法重建了一种可能的束团纵向分布。实验结果表明，当束流宏脉冲峰值强度约为24 mA，即电荷量约为15 pC时，电子束团均方根长度约为0.723 5 ps。电子束团长度测量的研究可优化束流品质，对后续高能电子成像实验有重要的参考意义。

感谢清华大学梁一凡提供的帮助及有益讨论及德国DESY Prach Boonpornprasert博士的实验指导。