基于贝叶斯分类器的核电厂事故诊断方法研究

齐 奔，梁金刚，张立国，童节娟

(清华大学 核能与新能源技术研究院，北京 100084)

核应急是核安全纵深防御的最后1道防线[1]。福岛核事故后，业界更加关注核应急决策技术研究，核应急的首要环节是对核事故快速准确诊断[2]。人工智能(AI)技术，诞生于1956年，经历知识驱动和数据驱动两大阶段，目前正向第3代迈进[3]。自20世纪80年代，AI技术在核电厂事故诊断方面开始应用[4]，其后的发展与AI技术发展紧密相连。基于专家系统的核电厂事故诊断方法[5]，是基于知识驱动的第1代AI技术在核电厂上的应用案例，该方法由故障诊断知识库、综合知识库、故障诊断推理机等组成，通过将监视的物理征兆导入故障诊断推理机，并由故障诊断推理机与诊断知识库交互，求解出能解释物理征兆的事故类型，从而完成诊断步骤。这种方法的缺点在于完全依赖领域专家经验知识，缺乏足够的数学基础。第2代AI技术采用数据驱动方式，如神经网络[6]、支持向量机[7]等方法，由于具备坚实的数学基础，允许使用者仅提供原始的特征数据，无需领域知识的帮助。基于神经网络的核电厂事故诊断方法[8]，利用样本训练神经网络得到能识别事故网络模型，是目前基于第2代AI技术的核电厂智能化诊断方法研究中最为活跃的方向之一。但目前这种方法面临两方面的挑战，第一，它采用数据驱动方式，对数据的数量和质量均有着较高的要求：数据量不足，将不能够训练出合适的网络结构；数据质量过差，使得网络的推广能力严重下降。对核电厂事故诊断来说，缺乏大量真实事故数据，高度依赖仿真机对真实事故数据的仿真能力[9]，仅能使用仿真机作为数据源来训练样本，并且事故发生后很大概率面临着数据的缺失问题。第二，神经网络的运作原理目前不能充分的解释，即“黑盒”性质，对监管极严的核电厂来说，这种不可解释性将被认为可能隐藏巨大风险，是难以被接受的。第3代AI技术期望将第1代AI技术的知识驱动和第2代AI技术的数据驱动结合，克服各自的局限性[10]，而将第3代AI技术应用在核电厂事故诊断上的目标便是增强前两代智能化核电厂事故诊断的方法的鲁棒性和可解释性。

本文提出将贝叶斯分类器技术引入到核电厂事故诊断中，利用贝叶斯分类器方法本身提高诊断方法的鲁棒性，并以图论方法表达各物理征兆间的逻辑关系，提高诊断方法的可解释性。

1 贝叶斯分类器原理及类别

贝叶斯分类器是一种概率模型，主要利用贝叶斯公式解决分类问题，而核电厂事故诊断本质上也是一个分类问题。贝叶斯公式[11]如下：

(1)

式中：c为样本类别的集合{c1,c2,…,cN}，对应于核电厂事故的类型；x为样本，该样本包含m个属性{x1,x2,…,xm}，对应于核电厂事故相关的物理参数；p(c)为先验概率；p(x|c)为样本x相对于类标记c的类条件概率，或称为“似然”，对应于核电厂发生某种事故下相关物理参数表现某种状态的概率；p(x)为用于归一化的证据因子。求解上式时，p(x)和p(c)可直接确定，关键是计算类条件概率p(x|c)，它是所有属性的联合概率。在机器学习领域，根据求解该联合概率方法的不同，贝叶斯分类器主要分为以下3种。

1.1 朴素贝叶斯分类器

考虑到基于有限训练样本直接估计联合概率时在计算上将会遭遇组合爆炸问题，在数据上将会遭遇样本稀疏问题，属性越多，问题越严重。朴素贝叶斯分类器采用属性条件独立性假设：对已知类别，假设所有属性相互独立。换言之，假设每个属性独立地对分类结果产生影响[12]，如图1所示。

基于属性条件独立性假设，贝叶斯公式可重写为：

(2)

对于特定样本，上式中分母均一致，因此分类的判别准则为：

(3)

对于朴素贝叶斯分类器，又可分为离散型朴素贝叶斯和高斯型朴素贝叶斯，其中离散型是指样本属性呈离散状态，可通过统计计数的方式计算条件概率，而高斯型朴素贝叶斯直接处理连续性数值的样本属性，将条件概率分布认为是高斯分布，如式(4)所示，求解该条件概率仅需确定在训练样本中不同类别下该属性的均值和方差即可。

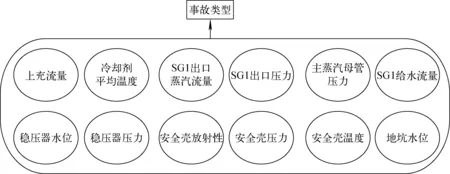
图1 朴素贝叶斯结构示意图Fig.1 Naive Bayes structure diagram

(4)

1.2 半朴素型贝叶斯分类器

考虑到朴素贝叶斯分类器基于属性条件独立性假设，在现实中通常很难成立，适当考虑一部分属性间的相互依赖信息，从而既不需完全进行联合概率计算，又不至于彻底忽略了较强的属性依赖关系。独依赖估计是半朴素贝叶斯分类器最常用的一种策略[13]。计算方法如下：

(5)

该方法假设每个属性在类别之外最多依赖于1个其他属性，既然属性条件独立性假设可获得泛化性能的提升，能否考虑增加属性的个数进一步提升泛化性能呢？不能，属性的增加导致训练所需的样本数量将以指数级增加，若数据充足，泛化性能可提升，但样本有限的情况下，求解高阶联合概率将成问题。

1.3 贝叶斯网络

为解决半朴素贝叶斯分类器，在有限的样本下求解高阶联合概率难题，引入贝叶斯网络[14]。基本的贝叶斯网络如图2所示，其中字母代表节点，箭头代表因果关系，例如A与B节点及两者之间的箭头，表示A为B的父节点，B为A的子节点。对于整个贝叶斯网络，A为根节点，D、E为顶节点。领域知识在贝叶斯网络的体现主要是网络中节点与节点之间的因果逻辑关系和条件概率的确定。该网络借助有向无环图来刻画属性间的依赖关系，并使用条件概率表来描述属性间的联合概率分布。贝叶斯网络的优点在于在有限的训练样本条件下，可引入领域知识和专家认知构建网络，以避免机器学习方式求解高阶联合概率的障碍。

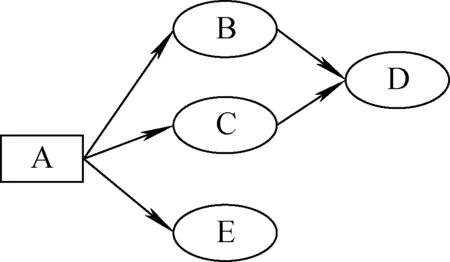
图2 贝叶斯网络Fig.2 Bayesian network

综合上述分析，依据属性间依赖的程度，将贝叶斯分类器看成1个“谱”：朴素贝叶斯分类器不考虑属性间依赖性，贝叶斯网能表示任意属性间的依赖性，二者分别位于“谱”的两端；介于两者之间的则是一系列半朴素贝叶斯分类器，它们基于各种假设和约束来对属性间的部分依赖性进行建模。

2 贝叶斯分类器在核电厂事故诊断中应用研究

将贝叶斯分类器应用于核电厂事故中通常需要3步：1) 事故诊断前的数据准备；2) 确定贝叶斯公式的“先验”概率；3) 应用不同的贝叶斯分类器，进行诊断结果分析。

2.1 事故诊断前的数据准备

本文数据来源为基于M310堆型设计的仿真机，按照该仿真机的特点，选取的核电厂3类不同破口尺寸事故(LOCA(大破口失水事故),MSLB(主蒸汽管道破裂),SGTR(蒸汽发生器传热管破裂))案例共300个。根据仿真机测试流程说明书针对核电厂不同事故下的物理征兆选择提取1 min时长的12个物理参数，如表1所列。

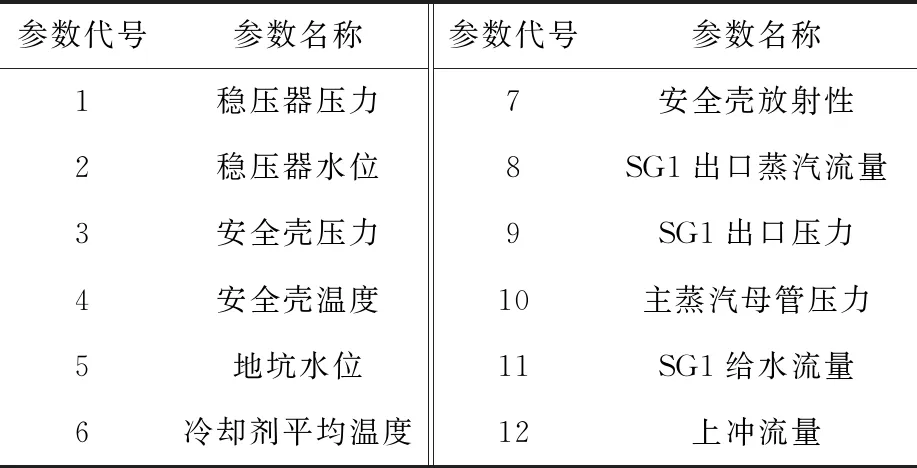
表1 监视参数Table 1 Monitored parameter

2.2 确定贝叶斯公式中的先验概率

与经典统计学中认为可用公理化定义的具有非负性、正则性和可加性的概率不同，在贝叶斯学派中认为先验概率是一种主观概率，而主观概率是人们根据经验对事件发生机会的个人信念的强弱。确定该主观概率的方法有以下3种：1) 对事件进行对比确定相对似然性；2) 利用专家意见；3) 利用历史资料[15]。针对核电厂不同事故类型的先验概率，本文采用以下两种方法确定先验概率分布。

1) 事故发生可能性对比确定相对似然性

根据自身的领域认知认为不同事故的发生概率一致，因此先验概率是均匀分布的；

2) 利用历史资料

根据红沿河核电厂PRA报告中对不同事故的发生频率来估计事故类型的先验概率分布(简称PRA估计分布)。

2.3 应用贝叶斯分类器诊断

由于半朴素贝叶斯分类器中属性最多考虑受两个属性的影响，而贝叶斯网络相比于该方法更适合表达事故下多个属性的相互影响，因此本文主要验证朴素贝叶斯分类器(包括高斯型和离散型)和贝叶斯网络两种贝叶斯分类器的效果。贝叶斯分类器模型构建思想为：将300个各类型事故构成的数据集，划分为训练集和测试集，利用训练集构建贝叶斯分类器，用测试集检测训练所得贝叶斯分类器的性能即诊断准确率，后续小节中对各贝叶斯分类器的诊断验证便是基于该思想进行的。而应用于实际核事故中，其诊断思路是：在事故发生后，得到事故相关各物理参数监视值，欲确定核事故类型，利用事先训练好的贝叶斯分类器进行诊断，以达到快速核电厂事故诊断目的，诊断结果为核应急后续环节如源项估计、后果评价和防护行动建议等提供技术基础。

1) 朴素贝叶斯分类器诊断方法

首先采用离散型贝叶斯分类器验证两种先验分布(均匀分布和PRA估计分布)的影响。提取事故发生后第6 s的数据作为数据集。选取数据集的80%作为训练集，其余20%作为测试集，并采用蒙特卡罗交叉验证方法，诊断结果显示均匀分布诊断准确率为98.82%，PRA估计分布诊断准确率为95.30%，可看出，不同的事故先验分布对诊断准确率的影响较小，这也进一步验证了贝叶斯定理用于诊断时，粗糙的先验分布经过似然函数的修正可显著减小对后验分布(诊断结果)的影响。同时对于核电厂事故这种实际发生概率在百万分之一以下的事件，在进行后续诊断时，由于缺乏足够充足样本，将其分布认为均匀的，是符合贝叶斯定理应用情景的。确立先验分布后，将离散型和高斯型贝叶斯分类器用于事故诊断。

(1) 离散型朴素贝叶斯分类器诊断方法

本研究通过观察6 s时各样本物理征兆的差异显著度划分如表2所列的破口范围。

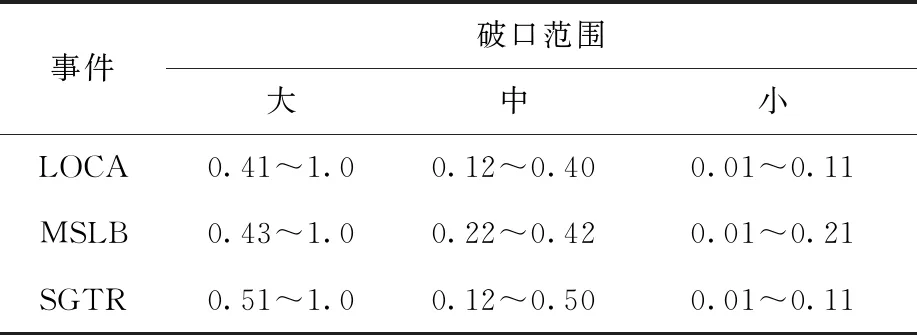
表2 划分范围Table 2 Dividing range

离散型朴素贝叶斯分类器诊断思路是：事故发生后，得到了1 min内12个物理参数监视值，并不确定核事故类型，基于PyCharm平台，编写Python程序，对事故发生后1 min内的数据进行事故类型的持续诊断，诊断准确率随时刻的变化如图3所示。

经计算事故诊断结果的准确率均值在97%以上，证明基于朴素贝叶斯核电厂事故诊断方法的有效性。在事故发生的前几秒，由于小破口事故物理参数特征与正常工况的差异性并不明显，导致诊断精度较低，同时之所以在事故6 s附近诊断精度均为100%，这是因为在划分破口尺寸范围时，主要基于6 s时的各物理参数之间的差异性进行划分，导致6 s附近的诊断结果较为准确。

为进一步验证大、中、小尺寸破口范围对诊断结果的影响，依据不同时刻，观察物理征兆差异显著度，划分如表3所列的破口范围。在事故发生后的1 min内持续诊断准确率如图4所示。

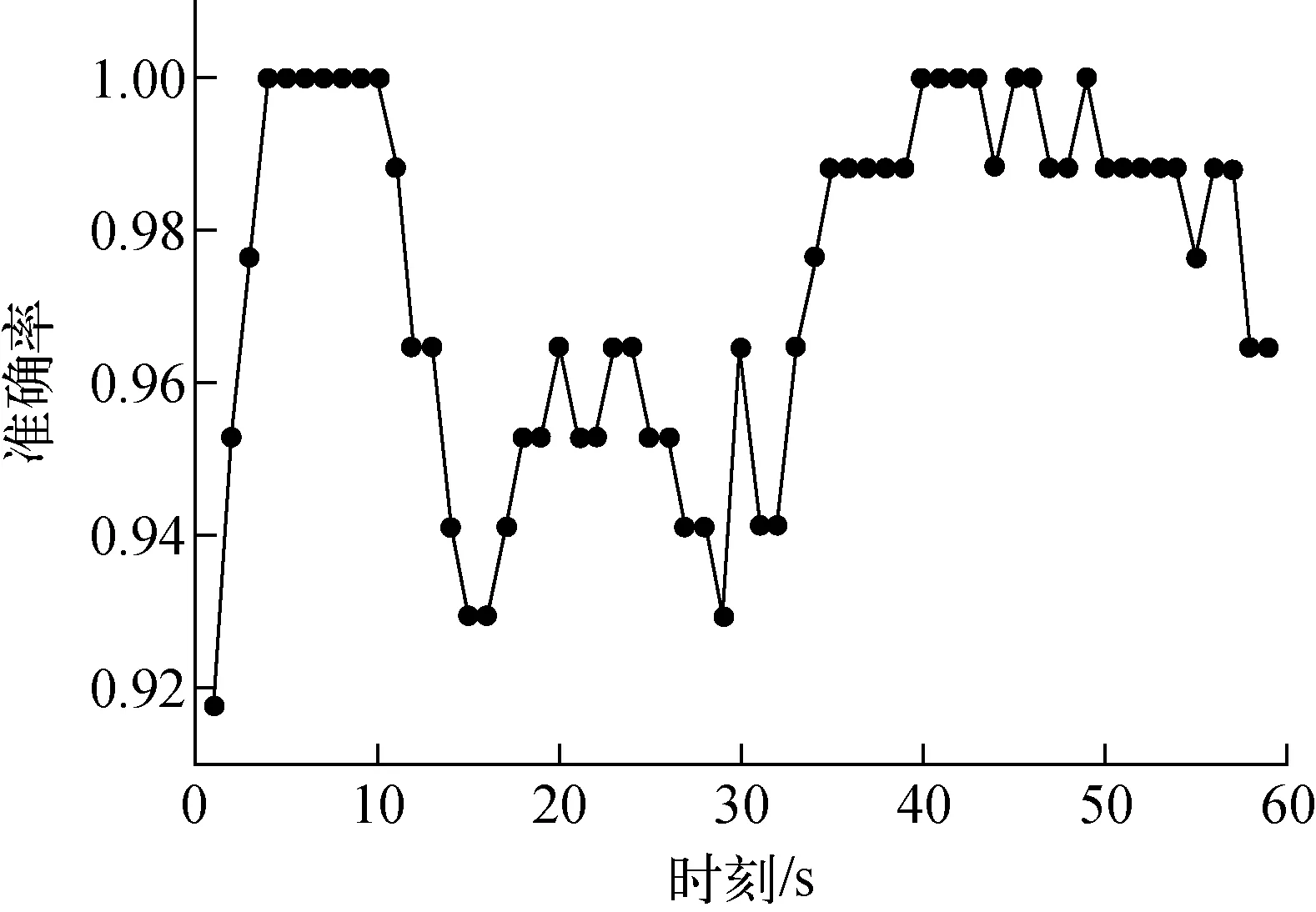
图3 离散型朴素贝叶斯诊断准确率Fig.3 Diagnostic accuracy of discrete naïve Bayes

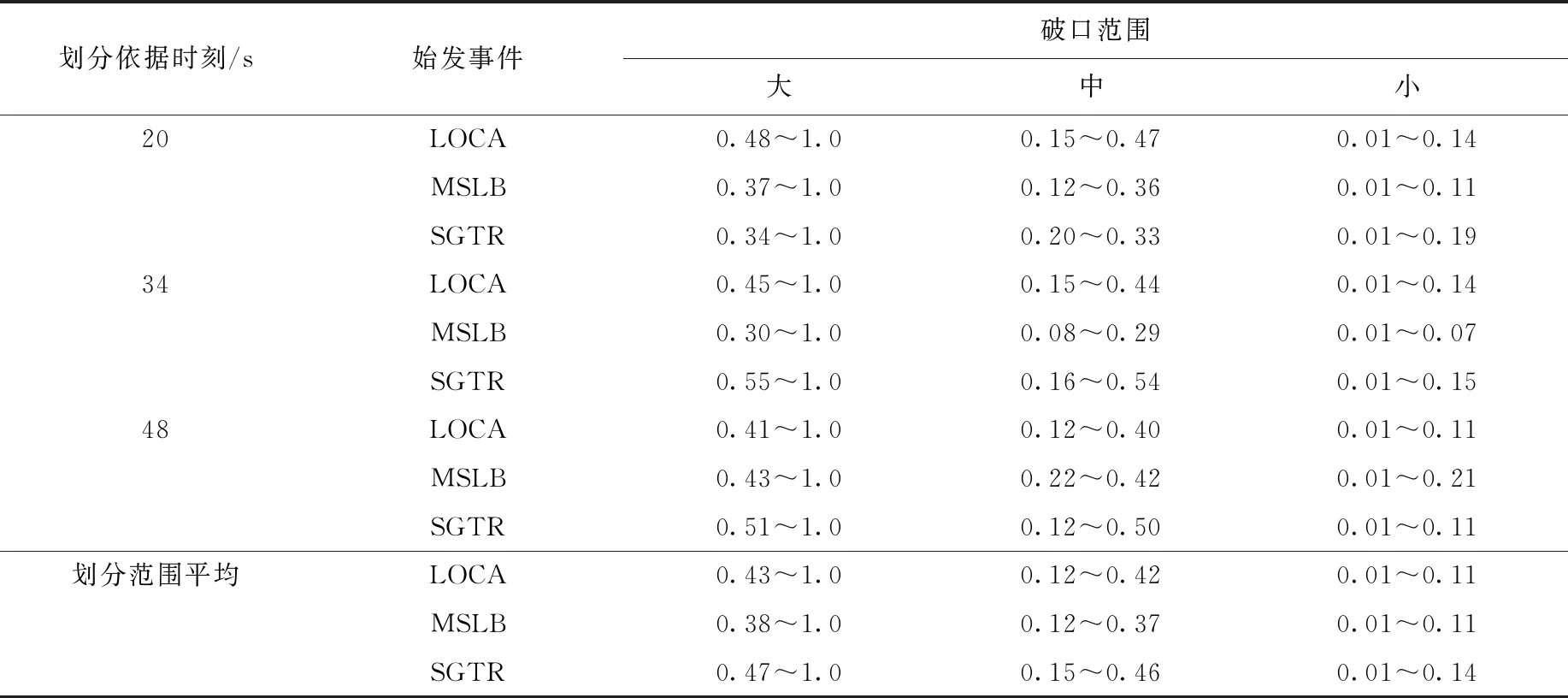
表3 不同破口归类范围Table 3 Classification range of different breaches

图4 不同划分方式诊断准确率Fig.4 Diagnosis accuracy rate of different classification methods

根据诊断结果可看出，无论是何种划分范围，其准确率均在91%以上。根据图4在不同的划分依据时刻附近(图中圆圈标记所示)准确率均为100%，可得诊断准确率一定程度上受大、中、小破口划分依据时刻的影响，这是因为该时刻附近样本差异性分布与依据该时刻进行划分的大、中、小破口范围一致性较高，从而导致该结果。根据上述分析，可看出朴素贝叶斯诊断方法有一定的错误诊断率，受划分范围依据时刻的影响，诊断准确率表现为一定的敏感性，其根本原因是物理参数转化为离散状态时，部分样本数据离散结果彼此之间差异性较弱。

(2) 高斯型朴素贝叶斯分类器诊断方法

根据离散型朴素贝叶斯分类器的验证结果，将采用均匀分布的先验概率和4类划分均值范围作为破口尺寸划分依据，进行诊断，如图5所示，诊断准确率均值在99.4%以上，高于离散型朴素贝叶斯诊断准确率均值。

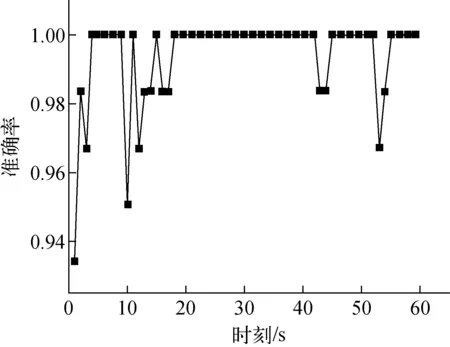
图5 高斯型诊断准确率Fig.5 Gaussian diagnostic accuracy

2) 贝叶斯网络诊断方法

图6 3类事故贝叶斯网络Fig.6 Bayesian network of three types of accidents

该诊断方法的第1步是进行贝叶斯网络的建模，根据PRA报告中针对3类事故物理征兆的描述，如对于一回路冷段大破口失水事故，该事故发生后将引起稳压器压力、稳压器水位、上充流量、安全壳压力、安全壳温度、安全壳放射性以及地坑水位这些物理参数变化，同时结合仿真机已有的测点信息，建立如图6所示的贝叶斯网络模型。建好模型后，还需添加条件概率表，主要根据领域专家知识添加节点与节点间的条件概率。

该方法采用朴素贝叶斯诊断方法相同的数据来源与数据离散过程，构建好贝叶斯网络模型后，编写Python程序，利用Pgmpy库完成模型和测试集的读入，并基于变量消去法进行精确推理，其诊断结果如图7所示，诊断准确率均值为62.5%。

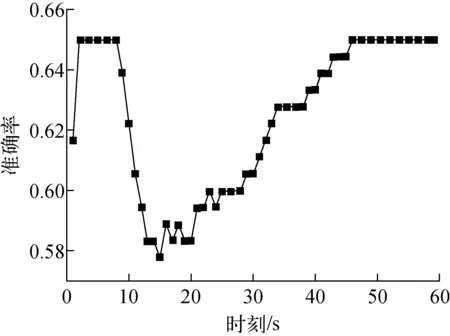
图7 贝叶斯网络诊断准确率Fig.7 Bayesian network diagnosis accuracy

2.4 不同的贝叶斯分类器性能对比

2.3节中先后采用了离散型朴素贝叶斯、高斯型朴素贝叶斯和贝叶斯网络3种分类器针对核电厂事故发生后1 min内的数据进行诊断，诊断准确率对比如图8所示。

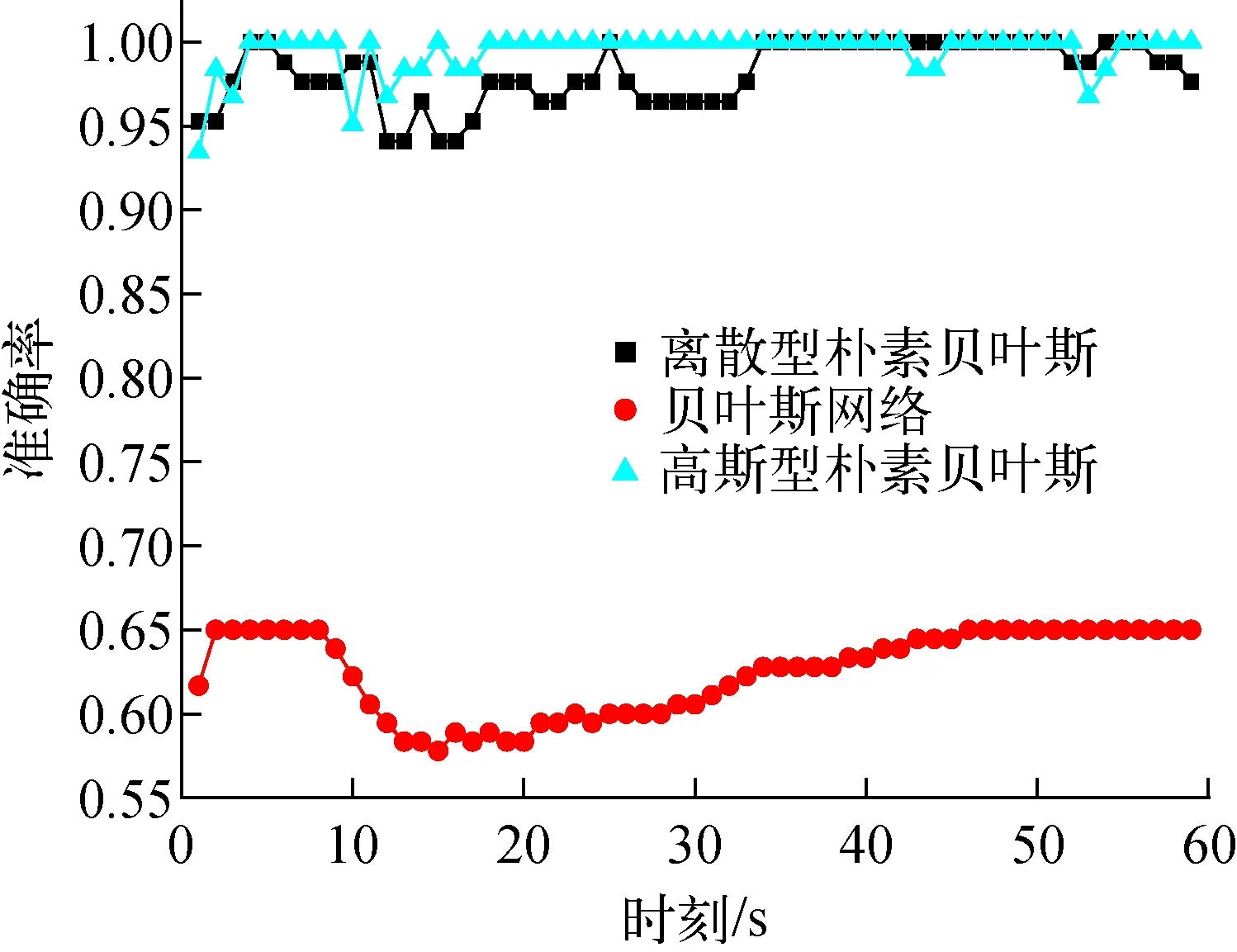
图8 不同分类器诊断结果对比Fig.8 Comparison of diagnosis results of different Bayesian classifiers

综合上述诊断结果，对比分析以下几个方面。

1) 准确率对比

根据诊断结果可看出贝叶斯网络诊断结果准确率显著低于朴素贝叶斯分类器，主要有以下两点原因。(1) 贝叶斯网络虽考虑属性间的相互影响，但整个建模过程中，引入了较大的人为不确定性，数据挖掘程度较浅，诊断结果误差较大。(2) 朴素贝叶斯分类器采用属性条件独立性假设，在现实中很难成立，但却能获得较好的诊断结果。一种解释是对分类任务来说，仅需各类别的条件概率排序准确、无需精准概率即可导致正确分类结果。另一种解释是，若属性间依赖对所有类别影响相同，或依赖的影响能相互抵消，则属性条件独立性假设在降低计算消耗的同时不会对性能产生负面影响。

2) 诊断效率对比

朴素贝叶斯分类器诊断步骤简单，不需要贝叶斯网络的建模过程，效率较高。尤其是高斯型朴素贝叶斯分类器不需要数据离散化处理，可直接对仿真机原始数据进行诊断。

3) 破口尺寸诊断精度

在确定事故破口程度时，人工建立的贝叶斯网络主要取决于自身对核电厂事故物理现象的定性认知，细化到破口的具体尺寸诊断时，由于相同类型的事故物理征兆较为类似，对破口具体尺寸的建模较难。而朴素贝叶斯主要基于数据驱动，可进一步诊断出事故的破口尺寸。

4) 事故可扩展性

朴素贝叶斯分类器诊断时，主要由程序完成诊断任务，理论上可无限制添加可能的事故类型进行诊断。而依赖于人自身建立的贝叶斯网路，在事故类型进一步扩展时，会引起网络节点组合爆炸问题，条件概率表的制定和推理算法的选择均将成问题。

5) 程序自主化诊断

朴素贝叶斯分类器完全可由1套编好的处理程序自动完成事故的诊断。而贝叶斯网络需要专家参与，建立贝叶斯网络等，将降低诊断时效。

3 结论与展望

核应急是核安全纵深防御的最后1道防线，以期减少对公众、环境的危害和降低经济损失。核应急一般包括机组状态诊断、源项估计、事故后果评价和防护行动建议等技术环节，而事故诊断是机组状态诊断的核心内容之一，领域专家期待在严重事故发生后的第一时间确定事故类型，将其作为后续核应急技术环节的基础。本文将贝叶斯分类器技术引入到核电厂事故诊断中，充分利用贝叶斯分类器相比于神经网络等智能化诊断技术具备的可解释性和鲁棒性优点，并进一步对比分析3种不同的贝叶斯分类器的性能，结果表明：

1) 高斯型朴素贝叶斯分类器诊断准确率最高，1 min内诊断均值在99.4%以上；

2) 朴素贝叶斯分类器在诊断效率、破口诊断精度、事故可扩展性、程序自主化诊断等方面有显著优势；

3) 贝叶斯网络为不确定学习和推断提供了基本框架，具备更高的可解释性和鲁棒性，未来可将机器学习引入到贝叶斯网路的构造中，进一步提高其性能。

作为一种智能化核事故诊断方法，朴素贝叶斯分类器方法(离散型和高斯型)主要基于数据进行构建，这使得该方法高度依赖仿真机对真实事故数据的仿真能力。因此，仿真机性能会影响朴素贝叶斯分类器实际应用诊断精度。而与高斯型相比，离散型朴素贝叶斯在原始事故数据基础上加入了领域认知，即将原本连续的事故数据离散成偏低、正常和偏高等状态信息，降低了对仿真机模拟数据的仿真度要求，且最终诊断准确率与高斯型相比变化较小。而贝叶斯网络作为一种摆脱仿真机数据依赖的尝试，在网络的构建阶段完全依赖领域知识，但最终的诊断性能相对于朴素贝叶斯分类器较差，这是由于贝叶斯网络构建过程中，节点间连接关系和条件概率具体数值的构建具有较大的不确定性，对网络构建者的领域知识要求较高，该方法可随领域专家知识的加强，进一步提高其性能，对于实际应用更具意义。除上述两种贝叶斯分类器外，对于假设属性符合多维正态分布的贝叶斯分类器[16]，在核事故诊断方面的性能有待验证。未来，将该方法与神经网络、支持向量机等方法做性能对比。

感谢红沿河核电厂在事故仿真数据方面的支持。