间隙度量模式下的闭环系统故障诊断实现

余伟,江艳,张凡

(1.佛山科学技术学院机电工程与自动化学院,广东佛山 528231;2.华南理工大学广州现代产业技术研究院,广东广州 510640)

1 引言

随着科学技术的发展,现代控制系统正在变得越来越复杂.由于系统结构的复杂性和外部环境的变化,如果故障发生而没有被及时诊断出来并得到有效处理,就有可能传播、演化成灾难性事故[1–3].因此,如何提高系统在运行过程中的安全性和可靠性,成为现代控制系统中的重大问题.故障诊断技术为解决上述问题提供了有效的方法,由于过去几十年的显著努力,故障诊断技术得到了快速发展,大量的研究成果得到了发表[4–7].

在实际系统中,为了使设备实现预期的生产目标,同时满足稳定性和鲁棒性等要求,通常需要对系统施加反馈控制.然而,现有故障诊断文献大多是为开环系统设计的,没有考虑反馈对故障诊断性能的影响[8].这些基于开环的故障诊断方法,为了实现对故障的敏感性、同时对干扰具有鲁棒性,一般采用系统传递函数矩阵的H∞,H2和L2等范数指标[9–11].但是这些工具都是基于欧氏距离的表象性能,难以有效解决闭环系统的故障诊断问题,因此有必要在闭环前提下研究故障诊断方法,以符合实际的工业需求,解决更实际的生产安全性问题[12].

目前基于闭环系统的故障诊断已有部分成果,文献[13]验证了转矩功率谱在开环系统下可以用来检测感应电动机的电气故障,但在闭环情况下用于开环操作的指标不再有效.文献[14]通过设计一个常规观测器和一个不受敏感器故障累积效应影响的特殊观测器结合,对无刷直流电机的典型输入和输出性故障型故障准确定位和隔离,但在使用这种方法时需要观测器与模型完全匹配,因此这种方法有很大的局限性.文献[15]通过设计增广系统观测器的方法对高速列车牵引电机闭环系统的传感器故障进行分析,这种方法可以减少故障在闭环系统内传播的影响,但对于控制效果、干扰对输出的鲁棒性和故障对于残差的可检测性不能兼顾,无法获得全局的解决方法,对于微小故障达不到相应的检测要求.

由于发生故障的系统与正常系统间几乎必然出现一定程度差异,因此,可以使用一种所谓间隙(gap)度量方法从系统角度来判别闭环系统之间的差异.早期gap度量技术广泛应用于鲁棒控制理论中的不确定闭环稳定性分析[16–18],经过近几年的发展,基于gap度量的方法逐渐被应用于故障诊断的研究领域中.文献[19]指出传统系统差异的度量可能无法准确预测闭环系统性能的变化,因此提出一种基于gap度量的方法可以作为对故障系统进行诊断的一种新途径.文献[20]和文献[21]采用v-gap度量对系统的故障严重程度进行分级分类研究,文献[22–24]提出将gap度量技术辅助故障检测与隔离的分析方法,目前这些方法还处于理论探索阶段.

受上述文献启发,本文针对包含不确定性和扰动的闭环系统,从系统整体角度出发,在间隙度量模式下,进行故障检测和分级分类,通过故障系统与正常系统的k-gap度量值为指标,将故障对系统的危害程度划分为多个界限清晰的故障等级,并依据同一级别故障系统之间的k-gap度量值,进一步对故障进行分类,最后通过数值仿真,对电机双闭环系统,验证本方法的有效性.

注1本文所采用的符号表示如下:

RH∞(RHm×n∞)表示稳定系统的所有(m×n维)实有理传递函数的集合;

H2表示所有信号的子空间,这些信号的能量是有界的,且K <0时为零;

H∞表示稳定的所有传递函数的集合;

sup表示上确界;

inf表示下确界;

Im×m(Ip×p)表示m×m(p×p)维单位阵.

2 预备知识

在本节中,首先简要介绍互质分解技术,在此基础上,引入gap度量,k-gap度量以及基于互质分解技术的故障模型一般形式相关基础知识.

2.1 互质分解技术

2.1.1 左互质分解和稳定核表示

则称它们为在RH∞上的左互质.

考虑一个线性时不变系统

则G的一个左互质分解可写成

由式(3)可知,系统模型式(2)可改写成

2.1.2 右互质分解和稳定像表示

则称它们为在RH∞的右互质.

一个传递函数矩阵G对应的右互质分解可以写成G=NM−1.更进一步系统模型可以等效表示为

由式(6),稳定像表示可以被描述为

其中v表示参考输入.

2.2 gap度量技术

2.2.1 图和gap度量

通过式(7)可以得到对于v∈H2,所有输入输出对(u,y)在H2中建立一个子空间并且它是闭合的.这个子空间被称为系统(6)的图,并且可以表示为

由式(8)可以得到图表示的一般形式

一般而言,间隙是指希尔伯特空间中两个封闭子空间之间距离的度量.令ϑ1,ϑ2是两个图,从ϑ1到ϑ2的有向间隙,通过表示,被定义为

ϑ1和ϑ2之间的gap度量被定义为

2.2.2 k-gap度量

间隙度量是在像子空间中定义的,它被广泛用于反馈控制系统的稳定性分析.对于故障检测性能的分析,核子空间中的度量是至关重要的,因此,引入k-gap度量作为两个核子空间之间的距离测量.为此,引入下面的图定义

类似于gap度量的图定义,式(14)表示所有输入输出对(u,y)在H2中建立一个封闭的核子空间,它的图表示可以被一个传递函数矩阵G的任意稳定核表示定义.为了测量两个不同图κ1和κ2之间的距离,根据有向间隙定义(10),可以引入以下k-gap度量的定义.

则有向k-gap可以表示为

类似于式(12)中给出的gap度量定义,可以引入k-gap度量的定义为

一般说来,k-gap度量是对H2中两个内核子空间之间距离的度量,这两个内核子空间分别由来自两个不同过程的输入和输出信号.此外,与gap度量不同的是,k-gap度量目前主要用来量化标称系统到不确定系统或故障系统的距离,因此,k-gap度量被更多用于故障诊断内容中.

接下来,给出上面引入的k-gap度量的计算方案.

式(18)给出了k-gap度量的近似计算.

2.3 基于互质分解技术的系统建模

在本节中,介绍基于互质分解技术建立无故障模型,在此基础上,推导出带有不确定性和扰动的故障模型一般形式.

2.3.1 无故障模型

假设标称系统(无故障和不确定性)模型描述为

其中:y∈Rm,u∈Rp,为了描述模型的不确定性和各种干扰,标称模型(19)可以扩展为

2.3.2 故障模型的一般形式

乘性故障:类似于处理模型不确定性的方式,将标称模型(19)扩展为

当同时考虑系统的不确定性、扰动、加性故障和乘性故障时,互质分解技术建立系统模型的一般形式可以描述为

3 基于k-gap度量的闭环系统故障诊断方法

在本节中,介绍基于互质分解技术的残差生成器和阈值设置方法,并依据k-gap度量值定义故障诊断指标.

3.1 残差生成器与阈值设置

3.1.1 残差生成器

对于标称系统(19),给出稳定核表示的一般形式

对于所有的线性时不变系统,一种参数化的残差生成器可以表示为

其中R∈RH∞是参数矩阵.

在故障诊断研究中,残差生成器式(24)的动态变化,在模型不确定性、系统扰动和待检测故障方面起着重要作用.假设系统动态过程由式(23)描述,则可直接得到

反馈控制回路是故障诊断中应用领域之一,考虑如图1所示的反馈控制回路.

图1 反馈控制回路Fig.1 Feedback control loops

它可以表示为

控制器:

输出:

反馈控制回路中:v是控制回路的参考信号,d表示扰动向量,K是反馈控制律,G表示具有互质因子不确定性的对象模型.假设系统中存在乘性故障,将残差生成器式(24)运用到反馈控制式(27),可得式(30).

3.1.2 阈值设置

在后续研究中,用L2范数评估残差信号r0.假设

其中:δ∆表示系统不确定性,δ∆d表示扰动不确定性,δ∆,δ∆d∈(0,1).

从残差生成器式(30)可知,闭环系统阈值为

参考信号v一般都是在线设置或计算的,并且J(K,G)取决于模型的不确定性,给出闭环系统的阈值设置公式如下:

3.2 故障检测指标

显然,由式(36)可知,一个更大的δK(K0,Kf)意味着更强的故障可检测性.在考虑系统的不确定性和扰动时,通过阈值设置式(33),可以给出以下基于k-gap度量的故障检测逻辑:

∥r0∥2≤Jth故障未发生;

∥r0∥2>Jth故障发生.

3.3 故障分级分类指标

如果系统发生的故障对系统的危害性很小,就可以认为是小等级的故障,否则就可以认为是其他等级的故障[25–27].按照故障的危害程度进行分级,可以为后续系统容错控制提供重要依据.为实现对闭环系统故障进行分级分类,可以采用k-gap度量值作为故障分级分类指标.

故障对系统性能的危害程度可以依据k-gap度量值的大小来划分系统故障严重等级,故障分级图如图2所示.

图2 k-gap度量故障分级示意图Fig.2 Diagram of k-gap metric fault gradation

小故障等级:0<δK(K0,Kf)≤ξ1;

中故障等级:ξ1<δK(K0,Kf)≤ξ2;

大故障等级:ξ2<δK(K0,Kf)≤ξ3;

严重故障等级:ξ3<δK(K0,Kf)<1.

同一级别的故障其闭环特性也会有所不同,因此可以进一步将同级别故障进行分类,故障分类图如图3所示.

图3 k-gap度量故障分类示意图Fig.3 Diagram of k-gap metric fault classification

基于上述的分级机制,每一故障等级都需要一个阈值,因此可以依据故障模型之间的k-gap度量值设置多级阈值ςi(0<ςi <1,i=1,2,3,4),同级别故障模型之间的k-gap度量为δ(fi,fj)(i,j∈N+).给出基于k-gap度量的故障分类逻辑如下:

δ(fi,fj)≤ςi同级同类故障;

δ(fi,fj)>ςi同级不同类故障.

4 仿真验证

4.1 电机双闭环系统

转速、电流反馈控制的电机双闭环系统凭借其优良的静、动态性能在现役飞机、电动汽车和工业伺服驱动等领域被广泛应用.

根据电机统一理论,采用磁动势相等原则,多相电机可以等价为两相电机,原始坐标经过坐标变换,可变换到旋转坐标dq轴下,采用转子磁链定向控制策略,等效为一台直流电动机[28].等效电路如图4所示.

图4 多相电机等效电路图Fig.4 Equivalent circuit diagram for multi-phase motors

电机双闭环系统的动态结构框图如图5所示,其中W1表示转速环PI调节器,W2表示电流环PI调节器,WS表示电力电子变换装置,WTl表示电机的电磁环节,WTm表示电机的机电环节.

在图5中,为了获得良好的静、动态性能,转速和电流两个调节器一般都采用PI调节器.根据陈伯时主编的教材[29],设计电机双闭环系统各环节传递函数如表1所示,使电机双闭环系统的动态性能达到最优.

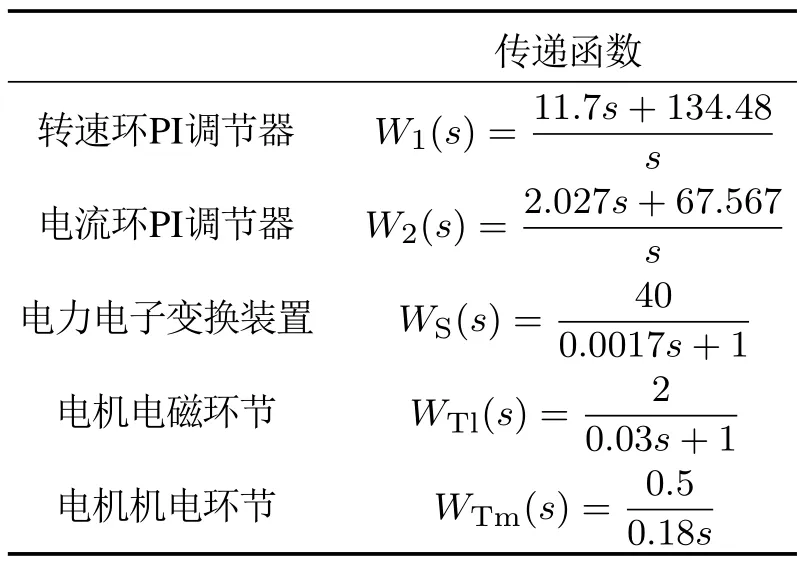
表1 双闭环系统各个环节传递函数Table 1 Transfer functions for each link of a double closed-loop system

图5 电机双闭环系统动态结构框图Fig.5 Block diagram of the dynamic structure of a double closed-loop motor system

在实际应用中,系统的不确定性和扰动是不可避免的,带有不确定性和扰动电机双闭环系统模型可以由式(20)来表示.其中互质分解因子不确定性的H∞范数界限应满足式(31),设定δ∆=0.01,δ∆d=0.02,负载扰动d=2,输入电压u=1 V.上述设计的带有系统不确定性和扰动的电机双闭环系统(标称系统G0)传递函数为

4.2 故障检测

针对电机双闭环系统中的不同程度乘性故障和执行器故障,以Fij(i=1表示乘性故障,i=2表示执行器故障;j=1∼9,分别表示10%∼90%故障严重程度)为故障程度因子,取值范围为0.1∼0.9.分别选取机电时间常数变化和转速调节器增益变化作为乘性故障和执行器故障,具体表示为WTm(s)=整个仿真时间设为5 s,在t=2 s时刻分别加入不同程度的乘性故障和执行器故障.

传统故障检测方法一般采取提取故障特征量的方法来判别系统的异常情况.当电机双闭环系统分别出现不同程度乘性故障(F11,F13,F16和F18)和执行器故障(F21,F23,F26和F28)时,采集电枢电压和电枢电流作为故障特征量,采用文献[30]中的平均能量法设置阈值Jth=±0.0949,故障检测结果分别如图6–7所示.

由图6(a)可知,发生乘性故障后故障超过阈值时间约为0.2 s,电枢电压故障残差最大幅值为0.57 V;由图6(b)可知,故障超过阈值时间约为0.3 s,电枢电流故障残差最大幅值为1.35 A.因此在采用传统的故障检测方法时,故障出现的时间短,在检测时难以捕捉,不同故障特征量产生的残差大小不同,极易受系统量纲的影响,故障出现之后很快被双闭环系统反馈控制的作用所抑制,导致无法对故障进行有效检测.类似于乘性故障,如图7所示,在发生执行器故障后也呈现出上述特点.

图6 乘性故障检测图Fig.6 Multiplicative fault detection diagram

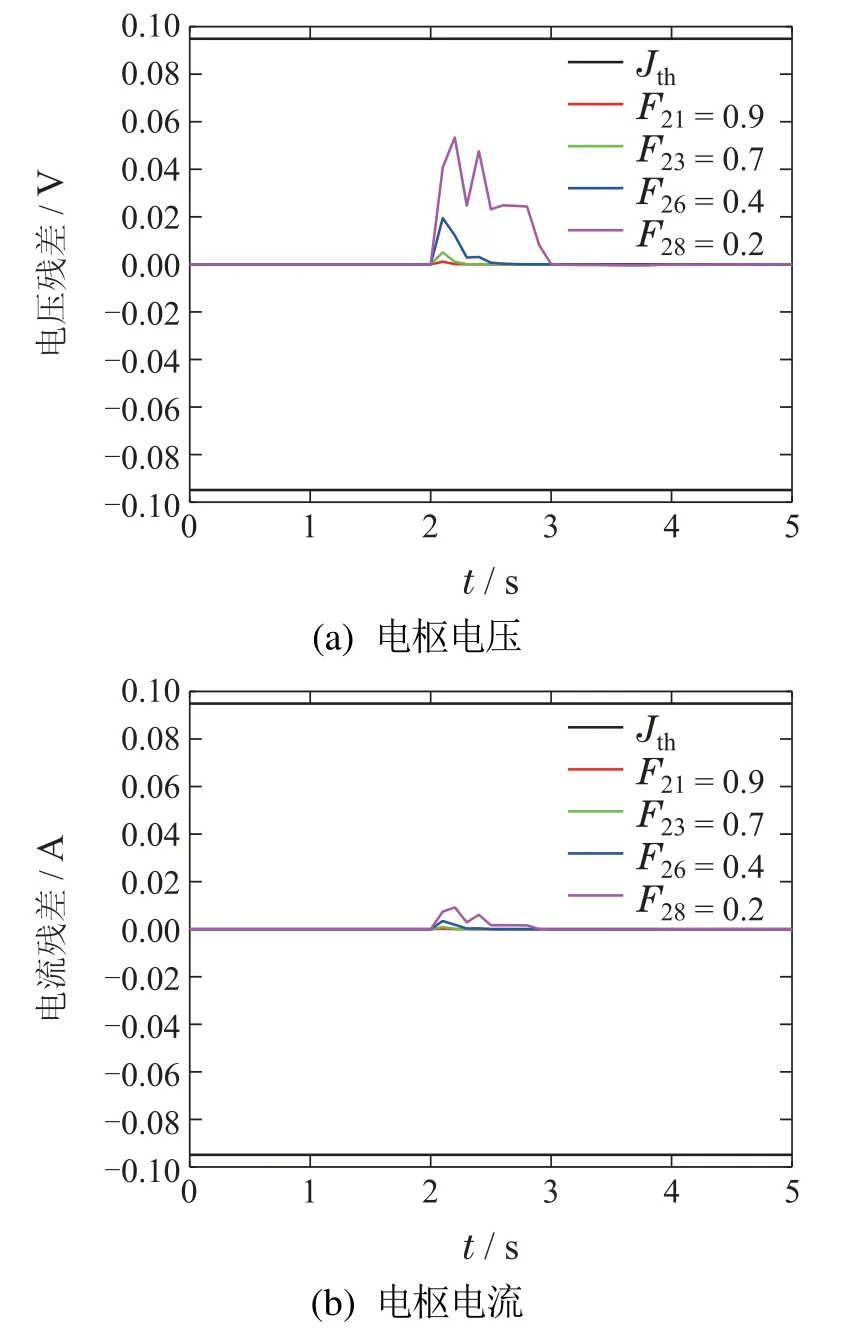
图7 执行器性故障检测图Fig.7 Actuator fault detection diagram

针对欧氏距离的表象性能,难以有效解决闭环系统的故障检测问题,采用k-gap度量的故障检测方法在同等条件下进行仿真分析.

不同程度的故障模型GFij与标称模型G0之间的k-gap度量值分别如表2所示.

表2 不同程度故障模型与标称模型的k-gapTable 2 k-gap for different degrees of failure models with nominal models

由表2可以看出,随着故障程度的增加,故障模型与带有不确定性和扰动模型之间k-gap度量值也不断增大.由闭环系统阈值设置式(33)可以得到阈值Jth=4.4671,基于k-gap 度量的残差,对电机双闭环系统不同程度的乘性故障和执行器故障,故障检测结果分别如图8–9所示.可以看出随着故障程度的增加,故障可检测性也不断增加,k-gap度量方法从系统的角度进行故障检测,不会受到量纲的影响,并且故障发生后不会受到双闭环系统反馈控制的影响.

图8 基于k-gap度量的乘性故障检测Fig.8 Multiplicative fault detection based on the k-gap metric

图9 基于k-gap度量的执行器故障检测Fig.9 Actuator fault detection based on the k-gap metric

4.3 故障分级分类

根据表2中故障系统和标称系统间的k-gap度量值(反映了故障对系统的危害程度),由故障分级机制将电机双闭环系统划分为如下4个不同的故障严重程度等级:

依据电机双闭环系统分级结果,接下来,对同一等级故障进行分类.因在实际闭环控制系统中,理论上当两个不同等级故障发生时,容错控制会进行控制器切换,所以进行两个不同等级故障分类划分,无实际意义.因此,表3给出了故障在同一等级下,依据不同程度故障模型之间的k-gap度量值,对应上述4个故障等级(小、中、大、严重),得到各级的分类阈值为0.1,0.3,0.5和0.7.例如,对于小故障等级,故障模型之间的k-gap小于0.1时被认为两个故障为同级同类故障,否则为同级不同类故障,其余故障等级分类机制与小故障等级相同.根据各级的分类阈值,可将电机双闭环系统,同级故障分类结果如图10所示.

表3 同等级故障模型之间的k-gapTable 3 k-gap between fault models of the same grade

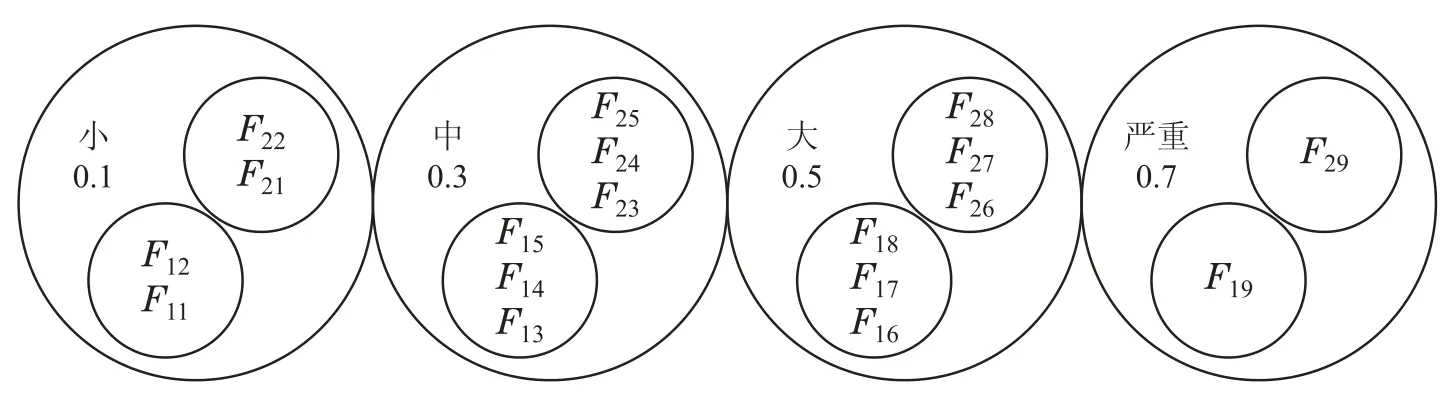
图10 电机双闭环系统故障分类图Fig.10 Motor double closed loop system fault classification diagram

5 结论

针对闭环系统的故障诊断,现有基于解析模型的方法中,基于物理数值的偏差(残差估计)只是表象,极度依赖于每个分量的物理量纲.为克服难以刻画其内在本质变化的困难,本文从间隙度量这一新的视角出发,针对包含不确定性和扰动的电机双闭环系统,根据故障模型与标称系统模型,以及故障模型之间的k-gap度量值,得到了故障检测和故障分级分类的具体实现过程.结果表明,此方法有利于闭环系统故障检测和不同类别故障评级分类,对后续容错控制器选择提供判据,此方法也可用于风险投资相关闭环系统诊断.