基于视觉SLAM–伺服框架的移动机器人指令滤波反步控制

李晨萍 张雪波 王润花 李宝全方勇纯

(1.南开大学人工智能学院机器人与信息自动化研究所,天津 300350;2.南开大学新闻与传播学院,天津 300350;3.天津工业大学电气工程与自动化学院,天津 300160)

1 引言

移动机器人具有运动空间大、运动灵活等优点;同时,低成本的单目相机能提供丰富的环境信息,因此利用单目相机反馈的图像信息来实现位姿镇定[1–2]或轨迹跟踪[3–4]的移动机器人视觉伺服发展迅速,在家庭服务、智能运输、自主停车等方面得到了广泛应用.

移动机器人本身的非完整约束给伺服控制器的设计带来了挑战,Brockett定理阐明了不存在光滑非时变的控制器完成移动机器人的位姿镇定[5],因此位姿镇定伺服控制器设计比轨迹跟踪控制器设计更加困难.移动机器人的非完整约束和单目相机的未知深度都是伺服控制器设计需要考虑的问题.文献[6]设计了分段连续控制策略,进而实现在部分视觉参数未知情况下的有限时间饱和镇定问题;文献[7]通过单应矩阵的元素构造状态变量,利用切换控制器将伺服镇定控制分原地旋转、移动至期望位姿正前方或正后方、直线运动三阶段进行;Shi等人[8]利用先验信息投影预测的方法处理陆标被遮挡的特殊情况,同时利用强化学习调整相关参数进而保证伺服的效率;文献[9]提出一种模糊自适应控制策略,使用两个独立的伺服增益解耦平移和旋转;Zhang等人[10]针对未标定的单目视觉伺服问题,提出一种自适应控制器实现移动机器人位姿镇定和轨迹跟踪.然而,上述方法都是运动学控制器,通过设计线速度和角速度进而实现控制目标.此类控制器在初始位置较大的误差信号下通常输出较大的速度,而由于惯性原因,设计的速度会与实际的速度有较大偏差,进而影响系统的性能.文献[11]从机械结构、执行器和能源3个子系统出发,设计了三级控制器,采用递阶控制器将3层控制器连接起来,最终实现移动机器人的动力学控制.但是该方法模型复杂,同时大部分商用移动机器人动力学参数未知且接口未开放,因此限制了动力学控制器的实际应用.文献[12]通过设计加速度的伪动力学控制器,进而积分得到光滑的速度信号,但是动态面方法滤波产生的误差被忽略,最终会影响系统的控制精度;同时,反步法不可避免的复杂求导计算以及单目相机造成的未知位姿尺度自适应更新也增加了控制器的计算负担.

针对移动机器人单目视觉伺服,本文基于SLAM的伺服框架基础[13],设计了图1所示的指令滤波反步控制策略.一方面,在SLAM感知模块中利用已知的速度信息,对未知尺度在线估计和优化,进而减小伺服控制器设计的复杂度;另一方面,伺服控制模块通过加速度信号的设计积分得到光滑的速度命令,进而减小SLAM的位姿预测模型误差;同时,指令滤波器的引入也避免了反步法的求导复杂计算.

图1 系统概述Fig.1 System overview

论文其他部分安排如下:第2节对移动机器人视觉伺服位姿镇定问题进行了系统建模;第3节介绍了SLAM感知模块;第4节设计了基于指令滤波反步法的位姿镇定控制器,并对其稳定性进行了分析;第5节通过仿真和实验验证了算法的有效性,同时与动态面方法的对比也体现了本方法的优势;最后一节对本文工作进行了总结.

2 系统建模

如图2所示,假定相机坐标系与移动机器人运动坐标系重合,即将相机光心垂直安装于移动机器人轮轴中心上方.令F表示固定于相机光心的坐标系,其中x轴沿光轴方向指向前,y轴垂直指向左侧.F∗和Fc分别表示固定于期望位姿和当前位姿的坐标系,θ表示Fc相对于F∗的旋转角,(∗xc,∗yc)是Fc原点在F∗的坐标,∗Tc=[∗Rc∗tc]表示Fc相对于F∗的变换矩阵,其中

图2 视觉伺服坐标系关系Fig.2 Coordinate systems relationship in visual servoing

根据移动机器人的特性,可以得到其运动学方程如下:

其中v和ω分别表示移动机器人的线速度和角速度.

定义(x,y)表示F∗原点在Fc的坐标,cT∗=[cR∗ct∗]表示F∗相对于Fc的位姿变换矩阵.根据位姿矩阵变换关系,可知,即

对式(2)求导,结合式(1)得到

为了减小机器人实际速度与设计速度信号的偏差,本文通过设计线加速度u1和角加速度u2的方法积分得到平滑的线速度和角速度信号,即

位置和姿态误差定义如下:

本文旨在设计u1和u2,驱动移动机器人运动至期望位姿处,即令位置误差ex,ey和姿态误差eθ趋于零.

3 SLAM反馈信号解算

基于文献[13]提出的SLAM–伺服框架,本文在图优化的SLAM模块中,添加了位姿节点之间的运动约束(如图3所示),继而利用式(5)得到反馈位姿的尺度因子

图3 SLAM位姿解算Fig.3 SLAM module for feedback signals estimation

其中:N表示初始地图中的位姿节点数量,Ri表示第i个位姿节点相对于初始位姿的旋转矩阵,ti+1表示第i+1个位姿节点相对于初始位姿的平移向量,s表示视觉模块的尺度因子,tim表示利用运动信息积分得到的第i+1个位姿节点相对于第i个位姿节点平移向量:

其中:vt和ωt分别表示两位姿节点的中间帧对应的线速度和角速度.

伺服过程中,SLAM模块应用前一帧的位姿和控制器输出的速度信息引导当前位姿的解算.具体而言,通过速度积分可以预测当前帧的位姿,进而预测地图点投影,辅助特征匹配.同时,位姿解算过程中,当前图像和地图点的3D-2D匹配以及和前一帧之间的运动约束均参与位姿优化

关键帧插入后的局部地图优化中,定义状态量χ=[T0··· TN1s P0··· PN2],利用伺服控制的运动信息和地图点投影观测值优化状态量

其中:N1是关键帧数量,s代表尺度因子,表示根据运动信息得到的第i个关键帧的预测平移向量,N2表示关键帧观测的地图点数量,Nj表示观测到第j个地图点的关键帧数目,ejk表示第j个地图点在第k个关键帧上的投影误差.

利用伺服控制器设计的速度信息,SLAM模块完成基于预测位姿引导定位的当前位姿解算.同时,SLAM因子图中添加了位姿节点之间的运动约束,进而恢复视觉反馈位姿信号的尺度因子,避免了伺服模型中因平移量的未知尺度带来的未知参数问题.伺服控制器设计过程无须考虑未知参数的迭代更新,SLAM模块恢复的尺度因子降低了控制器设计的复杂度.

4 基于指令滤波反步法的位姿镇定控制器

4.1 控制器设计

视觉伺服系统中,平移子系统和旋转子系统的开环误差模型分别

根据指令滤波反步法,平移系统跟踪误差状态量定义如下:

其中:exc和vc表示指令滤波αx和αv得到的信号,αx和αv分别表示状态量ex和v的虚拟期望控制指令.

同时,为了补偿滤波误差,定义平移系统的误差补偿状态量如下:

其中:ξy和ξx初值为0,导数设计如下:

ky,kx∈R+为正的常数增益.

将其作为指令滤波器的输入,滤波器的状态量zx,1和zx,2设计如下:

其中:ζ∈(0,1]表示滤波器阻尼系数,ωn >0表示自然频率;初始状态zx,1(0)=αx(0),zx,2(0)=0.指令滤波器输出信号为exc=zx,1和根据式(13),指令滤波器输出信号exc与输入信号αx之间的传递函数为

可以看出,该指令滤波器具有稳态单位增益.同时,该指令滤波器可以根据αx直接求解得到避免了反步法导数求解的复杂计算.

由式(12)可得˜ey的闭环动态方程如下:

结合式(9)–(10)和式(14),闭环误差补偿状态量vy的动态方程如下:

结合式(9)(11)和式(17),闭环误差补偿状态量vx的动态方程如下:

结合式(9)和式(20),可得闭环误差补偿状态量vv的动态方程如下:

与反步法相比,引入指令滤波器避免了虚拟信号求导带来的复杂计算量.尤其是加速度u1的计算过程中,如附录式(A.5)–(A.7)所示的反步法控制律需求解虚拟输入量的二次导数,计算繁琐;通过引入式(13)所示的指令滤波器,虚拟输入量的导数作为其输出信号可直接得到,避免了复杂的求导计算.

4.2 稳定性分析

定理1对于系统(6)–(9)和(22),控制律(12)–(13)(16)(19)(23)(25)可以使误差补偿状态量vy,vx,vv,旋转子系统状态量eθ,ω以及平移系统误差˜v均趋于0,即

定理1的证明可以通过以下步骤完成:

步骤1证明平移子系统误差补偿状态量vy,vx,vv∈L∞.

构造李雅普诺夫函数如下:

对其求导,并将式(15)(18)和式(21)代入,整理后可得

根据李雅普诺夫理论可知vy,vx,vv∈L∞.

步骤2证明旋转子系统状态量eθ,ω∈L∞.

根据模型(7)和(22),应用控制律(23)和(25),整理可得旋转子系统状态空间如下:

其中:a=kθkω+1>0,b=kθ+kω >0,故系数矩阵特征值位于复平面左侧.vy,sint∈L∞,所以系统控制输入kξvysint∈L∞.因此,旋转子系统状态量eθ,ω∈L∞.

步骤3证明平移子系统ωvy,vx,vv趋于0.

对式(30)两边积分可得

步骤4证明平移子系统补偿状态量vy趋于0.

定义f(t)=ωvy,因此有

对f(t)求导整理可得

其中:

对f1(t)求导整理可得

即f1(t)一致连续.

根据扩展芭芭拉引理,由式(34)–(37)可得

定义g(t)=f1(t),有

对g(t)求导并整理可得

其中:

结合eθ,vy,sint∈L∞,可以得到

对g1(t)求导整理可得

即g1(t)一致连续.

根据扩展芭芭拉引理,由式(39)–(42)可得

步骤5证明旋转子系统状态量eθ,ω趋于0.

步骤6证明平移系统误差状态量˜v趋于0.

对其求导,并将式(14)(17)和式(20)代入,整理后可得

因此式(46)可以转化为

其中

因此通过合理选择参数使k1,k2,k3>0,可以保证跟踪误差最终一致有界. 证毕.

注1文献[14]通过奇异摄动理论已证明指令滤波反步法的跟踪误差相对于标准反步法(如附录所示)的跟踪误差也是O(ϵ)数量级,即最终一致有界的边界会随滤波器频率ωn的增大而减小.

注2与动态面方法[12]相比,式(9)所示的滤波误差补偿机制,使指令滤波反步法的跟踪误差更小.

5 仿真与实验

5.1 仿真

为了验证算法的有效性,本文通过MATLAB对算法进行仿真,并与文献[12]中的动态面方法进行比较.

以固定于期望位姿的坐标系F∗作为参考坐标系,初始位姿为(−1.5 m,−0.3 m,22◦).指令滤波反步法的控制参数如下:

滤波器阻尼系数ζ=1,带宽ωn=30.

动态面控制律参数设置如下:

滤波时间常数τ=0.03.

仿真结果如图所示.其中图4表示指令滤波反步法的跟踪误差状态量变化曲线,跟踪误差最终均收敛至0.图5表示根据设计的输入信号积分得到的平滑的速度信号.

图4 指令滤波反步法的跟踪误差Fig.4 Tracking error signals of the command filter backstepping method

图5 机器人速度(指令滤波反步法)Fig.5 Velocities of the mobile robot in command filter backstepping method

图6是指令滤波反步法和动态面方法对应的误差信号变化曲线,最终的稳态位姿误差如表1所示.可以看出,指令滤波反步法比动态面方法收敛更快,精度更高.

图6 误差信号曲线Fig.6 Evolution of error signals

表1 稳态位姿误差比较Table 1 Comparison of control errors

5.2 实验

本文通过实验验证了算法的有效性.如图7所示,实验平台是Pioneer3-DX 差分移动机器人,并于轮轴中心上方安装了RealSense D435i相机(实验仅利用单目图像作为反馈信息),图像频率为30 Hz,分辨率为1280×720像素.用于图像处理和控制器计算的笔记本电脑配置为2.6-GHz Intel Core i7-6700HQ CPU.以期望位姿作为参考坐标系,设置初始位姿为(−1.33 m,−0.25 m,10.3◦).实验环境是无人工陆标的实验室自然场景,期望图像、初始图像和伺服完成采集的图像如图8所示.

图7 移动机器人视觉伺服实验平台Fig.7 Experimental platform of visual servoing

图8 视觉伺服图像(初始图像、期望图像、最终图像)Fig.8 Images captured during visual servoing experiment(initial,desired and final images)

图9和图10分别表示控制器输出的加速度、速度命令曲线和误差变化曲线.通过简单的平移运动进行SLAM的地图初始化和尺度初始化,该阶段角速度为0,设置固定的线加速度.之后通过两步法关联期望图像和SLAM地图,进而获得误差反馈信号.可以看出,即使初始位置具有较大的位姿误差,速度依然平滑增长;同时,期望位姿优化带来误差信号突变时,速度依然保持平滑变化,可以减小因惯性造成的执行误差引起的SLAM模块预测误差.

图9 加速度、速度命令曲线Fig.9 Acceleration and velocity signals

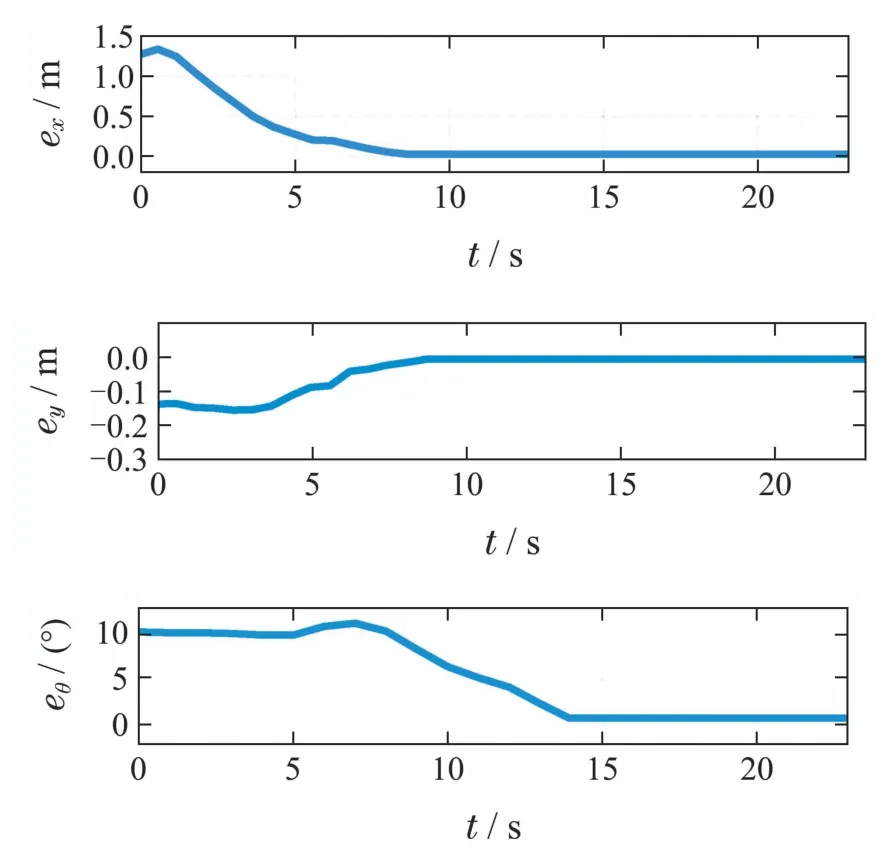
图10 反馈误差信号曲线Fig.10 Evolution of error signals in experiment

6 结论

针对移动机器人视觉伺服位姿镇定,本文设计了基于视觉SLAM–伺服框架的指令滤波反步控制策略,在解算反馈位姿的SLAM模块中,利用速度信息对单目未知深度信息引起的位姿尺度因子进行在线估计和优化,进而减小伺服控制器设计的复杂度;同时,伺服控制模块通过设计加速度积分得到光滑的速度信号,减小执行误差造成的SLAM位姿预测误差;基于指令滤波反步法的位姿镇定控制器,通过滤波误差补偿机制避免了动态面方法因滤波误差造成的系统误差.基于李雅普诺夫稳定性理论证明了闭环系统的稳定性,同时仿真和实验也验证了算法的有效性和误差补偿机制的优越性.

附录

平移系统反步法状态量定义为

其中exd和vd表示虚拟输入量,可得平移系统状态模型如下:

针对z1,z2子系统,设计虚拟期望输入量exd,vd如下:

针对跟踪误差状态量z3,设计线加速度u1如下:

其中:

旋转系统的反步法状态量定义为

其中:ωd表示虚拟角速度输入.因此旋转子系统状态模型为

对于z4子系统,设计虚拟输入量ωd如下

对其求导可得

考虑跟踪误差状态量z5,设计角加速度u2如下:

定理3对于系统模型(A.1)和(A.9),反步控制律(A.2)–(A.7)和(A.10)–(A.12)可以使系统误差收敛至0,即

构造李雅普诺夫候选函数如下:

对其进行求导,并将式(A.1)–(A.5)代入,可得

定理3证明与定理1证明类似:

1) 李雅普诺夫理论和式(A.13)–(A.14),可知z1,z2,z3∈L∞.

2) 根据反步控制律可知式(A.15)所示的旋转子系统状态空间,其中c=k4k5+1>0,d=k4+k5>0.系数矩阵特征根位于复平面左侧,因此旋转子系统状态量eθ,ω∈L∞.