无人机基站部署问题综述:模型与算法

靳晓洁 ,石建迈 ,伍国华 ,黄魁华

(1.国防科技大学系统工程学院,湖南长沙 410073;2.中南大学交通运输工程学院,湖南长沙 410075)

1 引言

小型无人机(unmanned aerial vehicle,UAV)具有机动性强、部署灵活、成本低等优点,在农业、物流、交通、环境、通信、军事等领域得到越来越广泛的应用.随着无线网络的发展与普及,无人机开始作为空中基站提供网络服务,为快速构建临时性无线覆盖网络提供有效支撑[1].特别在地震、洪涝、火灾等公共事件以及军事应急等突发情况中,以无人机为基站构建的无线网络为提高人员搜救效率提供了有力保障.

以无人机为基站构建无线网络时,决策者面临的一个重要问题是无人机部署位置优化,即如何优化无人机在三维空间中的位置为地面用户提供服务,以满足最大覆盖、节能可持续覆盖等目标.通过优化无人机部署,避免无人机之间的信号干扰,同时提高无人机的电池能量利用率、信号覆盖范围,可以得到高效的局域无线网络.近年来,无人机基站部署优化问题受到了国内外学者的广泛关注与研究,涌现出了大量研究成果.Sharma等[2]建立了无人机基站在辅助地面通信中的位置部署模型,使通信覆盖率最大.Lyu等[3]提出了一种无人机基站螺旋布局算法,同时优化无人机数量和信号覆盖率.Plachy等[4]将用户与最合适的静态基站或飞行基站相关联,通过优化飞行基站的位置,使数据传输速率最大.

无人机基站的部署优化可以看作一类新的选址优化问题,相对于传统的设施选址问题,无人机基站的部署问题面临更多新的挑战.首先,无人机在三维空间中移动时,起飞点和降落点要有一定面积的空旷区域,在飞行途中可能面临避障航迹规划问题;其次,无人机续航能力有限,其电池容量限制了有效载荷和持续工作时间[5],需要综合考虑飞行、服务时间与质量等的电量消耗;再者,当多个无人机同时作为分布式基站提供网络服务时,需要考虑无人机基站间的连通性及干扰情况,以提高网络服务的质量和效率.

而且需要考虑部署环境的影响,在郊区、一般市区、密集市区及高楼林立区域等不同环境中,无人机的通信传播概率不同[6].由于安全和隐私问题,无人机在应用中还有飞行干涉、禁飞区和最大飞行高度等限制,需要在这些约束条件下优化无人机基站的位置.上述挑战,增加了无人机基站部署问题的建模难度,需要考虑更多更复杂的约束条件.同时,也增加了部署优化问题的求解难度.理论上来看,无人机在连续三维空间的可选部署位置是无限的,各种约束又将解空间进一步分割.因此,高效的求解算法属于该领域的研究难点.

从当前无人机基站部署优化问题的总体研究来看,国内外学者在不同方面进行了大量探索性研究,但还缺乏系统的分析与综述.目前,只有Cicek等[7]在2019年的无人系统国际会议上对5G蜂窝网络中的无人机部署问题进行了较为系统的综述.为进一步促进该领域的发展,本文将近10年来无人机基站部署优化相关的主要文献进行了分析总结:首先分析了主要影响因素,包括覆盖半径、容量约束、能量消耗、连通性、干扰、用户分布和外部环境等;然后总结了当前主要的建模方法,从最大覆盖问题、集覆盖问题、p-median问题和p-center问题等方面进行了分类归纳;同时,整理分析了无人机基站部署优化问题的求解算法和验证实验;最后,探讨了该领域未来的主要发展趋势,为后续研究者理解无人机基站部署问题研究现状和开展研究提供参考.

2 影响因素

不同于传统二维平面或网络中的设施位置问题,无人机基站的部署一般是在三维空间,还需要考虑部署高度,以尽可能扩大覆盖范围.而且需要考虑无人机的容量约束、能量消耗、连通和干扰等自身特性,以及用户分布和环境条件等外部因素.

2.1 部署高度

无人机的部署高度是影响无人机覆盖范围的重要因素.无人机在越高的位置悬停,空对地传输的视线机会越大,其覆盖半径也越大,意味着无人机能够服务的范围越大.同时,部署高度增加,信号传输距离也会加大,造成更大的路径损失,进而影响用户接收信号的质量,使得覆盖服务质量变低.因此,部署位置需要在服务范围和质量之间均衡,过高过低都不是最优的决策.文献[8–11]等在满足服务质量的条件下,研究了使无人机覆盖区域最大的部署高度.文献[11]还对使传输速率最大的最优飞行高度进行建模.

2.2 容量约束

有容量约束的设施选址问题中,每个设施可提供的服务数量有限.同样,无人机也有容量约束.每个无人机可提供的总带宽是有限的,因此,为了满足用户的带宽需求,可服务的用户数量是有限的.这是无人机作为空中基站为地面用户提供网络服务的一个基本约束,在优化无人机基站位置时通常都会考虑[12–13].

2.3 能量消耗

一般无人机的能源消耗主要有两个方面:一是保持无人机空中盘旋姿态或者提供其飞行动力的能源损耗;二是无人机进行覆盖服务时的能源损耗,包括无线电辐射、信号传输和通信电路能量消耗等.而无人机的能源消耗主要受到无人机的大小、重量和功率(SWAP)约束,这在一定程度上决定了无人机的续航能力[1].目前无人机的续航能力都比较差,因此在部署无人机基站时,需要考虑如何降低功率实现节能[14–15],或者通过充电[16–17]进行能源补给.

2.4 连通性

在多无人机协同提供服务时,需要考虑无人机与用户间的关联,通过任务分配[18]将地面用户与无人机相关联.更重要的,需要考虑每个无人机与其他无人机的连通问题,这要求无人机与无人机间的距离要在一定范围内,才能保持无人机间的连通,进行有效的数据传输和信息交换[19–20].依赖于无人机间的连通形成特定的无人机网络,并且由于无人机的灵活属性,无人机网络具有拓扑可变化特性.在临时性或应急性的活动中,无人机网络可以随着用户移动不断变化形成新的拓扑网络.

2.5 信号干扰

每个无人机在提供网络服务时,都有一定的覆盖范围.而当使用相同频带的多无人机共同提供服务时,无人机间会产生一定的干扰,使得网络服务质量下降.Mozaffari等[9]研究了两个无人机提供服务时的最佳距离,使得无人机间的干扰最小,提供的服务质量最佳.Dong等[6]对每个无人机计算了所有周围的无人机产生的干扰,并称其为累计单元间干扰.Lin等[21]提出了一系列无人机通信中的干扰缓解技术.Mozaffari等[22]假设无人机使用不同频带,避免产生干扰.

2.6 用户分布

用户分布主要包括分布密度和分布状态(静止和移动).由于无人机容量有限,只能为给定区域的部分用户提供通信服务,因此覆盖给定区域用户所需的无人机数量与用户密度成正比[12].用户或设备作为无人机的服务对象,当他们处于静止状态时,无人机也可以处于静止状态提供服务,部署工作相对较为简单;而当他们处于移动状态时,则应该考虑如何部署无人机来适应移动用户,可以使无人机网络随用户进行自适应移动[23],也可以根据用户移动特性部署无人机网络进行服务[24].总之在部署过程中需要考虑用户密度及移动性,以为给定区域内的用户提供有效服务.

2.7 环境条件

文献[25]表示在高层建筑城市、密集城市、城市以及郊区,覆盖给定区域的同样数量用户,最后无人机的位置和覆盖区域有所不同.这是因为建立无人机无线覆盖模型主要通过空对地通信模型,而不同环境参数会影响通信传播概率.在部署无人机时,还需要考虑遮挡、禁飞区及最大飞行高度等环境条件:如果是在城市等具有高的建筑物或者遮挡物的区域,无人机的放置位置则有一定的高度限制;如果是在郊区等比较空旷的区域,无人机的放置高度则没有太多要求.另外,无人机在放置过程中,需要避开禁飞区以及不需要提供无人机服务的区域[26].Savkin等[27]研究了如何部署无人机来覆盖不平坦的地形.

3 模型

无人机基站的部署问题可以看作是设施位置问题的一个分支方向.覆盖范围和距离是衡量设施位置问题有效性的两个重要指标.根据覆盖特点,Laporte等[28]将覆盖选址问题分为最大覆盖位置问题(maximum covering location problem,MCLP)和集覆盖问题(set covering problem,SCP).根据距离因素,选址问题可以分为p-median和p-center问题.无人机基站部署问题通常抽象建模为上述4个基本选址问题,并根据具体情况进行扩展.

3.1 基于MCLP的无人机基站部署

MCLP是指在有限的设施数量和指定资源限制下,尽可能多地覆盖需求节点[29–31].很多情况下,无人机基站部署问题是考虑容量、能量、连接质量、干扰以及用户需求等约束条件下,在给定区域部署一定数量的无人机,使覆盖的用户数量最多.因此,基于MCLP,融合无人机覆盖的特有约束,进行扩展应用,是无人机基站部署问题的一类重要建模方法.Bor-Yaliniz等[32]研究了单个无人机在给定区域和用户数量下的三维最大覆盖部署问题.Sharma等[13]研究在MBS宏基站调控下的无人机最大覆盖部署,考虑了无线网络容量的影响.

基于MCLP的无人机部署建模,通常考虑能量消耗.Alzenad等[14]研究了单无人机在三维空间中的节能最大覆盖问题,增加了使发射功率最小的约束.Ruan等[15]提出一种基于节能通信的多无人机最大覆盖模型,将模型分解为最大覆盖和功率控制两个步骤.

在多无人机的最大覆盖部署建模中,通常要考虑无人机间的连接和干扰.Zhao等[20]在用户位置信息未知情况下,研究保持连通性条件的最大覆盖部署问题.Huang等[16]针对无人机在街道场景中为户外娱乐设备提供网络服务的场景,研究考虑充电情况下最大覆盖和最小干扰的部署问题.

基于MCLP的无人机部署建模,通常会考虑用户需求和用户分布.Lai等[33]在无人机最大覆盖中要求满足每个用户的数据速率,并且考虑了用户呈不同密度分布下的几种典型场景.文献[34–35]研究了用户具有不同QoS要求下无人机在三维空间中的MCLP,Klaine等[36]还增加了无人机回程和无线电接入网络的限制,同时考虑了用户的移动.

考虑数据速率[37]、链路质量[38]等网络性能的约束,也是无人机基站最大覆盖问题的一个重要研究方向.

3.2 基于SCP的无人机基站部署

SCP一般是在确保覆盖范围的前提下,尽可能降低设施数量或总体费用.基于SCP的无人机基站部署问题是在满足规定覆盖比例的前提下,融合无人机基站相关约束,优化所需无人机数量及部署位置.Mozaffari等[25]假设无人机基站具有相同的发射功率和高度,研究了覆盖半径为R的圆形区域所需的最少无人机数量.Lagum等[39]研究了地面网络存在下无人机基站部署的集覆盖问题.

能源消耗往往需要在无人机集覆盖问题建模时考虑.Li等[17]根据用户需求部署无人机,并考虑了充电问题,旨在优化多无人机通信系统的能源效率,以在城市地区实现无缝长期覆盖.

在多无人机的集覆盖问题建模中,通常要考虑无人机之间的连接和干扰.Zhao等[20]考虑在保持无人机间连通性情况下,研究如何确定无人机的最优数量和位置来覆盖给定位置信息的用户.Khuwaja等[40]考虑多个无人机产生共信道干扰,研究实现目标覆盖概率所需无人机的最少数量及位置.他们考虑了两种场景:一种是具有相同传输功率的无人机对称放置在相同的最优高度;另一种是具有不同传输功率的无人机非对称放置在不同的高度.

用户需求和用户分布也通常需要考虑.Kalantari等[12]考虑无人机的覆盖范围、容量、服务质量要求等约束,研究了不同用户密度分布情况下的集覆盖部署.Sharafeddine等[41]研究用户需求激增或受自然灾害影响的无人机基站的集覆盖问题.

很多无人机基站的集覆盖问题还考虑了无人机通信的网络性能[42],如通信延迟[43]、数据速率及吞吐量[44]等.

3.3 基于p-median的无人机基站部署

p-median选址问题由Hakimi(1964,1965)[45–46]提出,也被称为最小和选址问题.p-median问题是要确定p个设施在n个候选地点之间的最佳位置,从而使所有需求与其最近设施之间距离(或加权距离)的总和最小化.在应用p-median选址模型解决无人机基站部署问题时,通常将无人机视作设施,将用户或终端设备当作需求点,将传输功率、距离等作为成本,目的是找到总成本最小的无人机部署方案.Cui等[47]研究了单架无人机的室内最优部署问题,目的是使总传输功率最小化.Zahedi等[48]将无人机基站部署问题转化为一个p-median优化问题,其中p是覆盖用户所需的天线数量,目的是使用户和天线间的总距离最小.Sobouti等[49]将无人机在期望环境中的部署问题建模为基于p-median框架的数学优化模型,其中无人机使用动态信道分配或动态频率选择方法来避免干扰.

基于p-median的无人机部署建模,不仅考虑用户需求和分布,更注重用户的服务质量体验.Mozaffari等[22]研究无人机如何根据用户分布来移动和改变位置,并使用p-median设施建模框架进行求解.Shakhatreh等[50]研究了为高层建筑内均匀分布的用户提供无线覆盖的单个无人机部署问题,在满足室内用户速率要求条件下,使总发射功率最小.Savkin等[51]考虑了在保持无人机与固定基站连接的同时尽量减少无人机与用户间的平均距离的问题,使整体服务质量最大化.

3.4 基于p-center的无人机基站部署

p-center问题也被称为极小极大选址问题.与pmedian问题不同,p-center问题通过尽可能减少任何一个节点到其最近设施的最大距离来改善较远需求节点的服务,实现用户间的公平性.一般用于应急服务设施选址问题,如消防队、警局等公共救援设施以及自然灾害下应急物资供应中心等,尽可能快地使每个需求节点获得服务.在无人机的部署优化问题中,p-center问题类型相对较少,一般将无人机视为设施,用户或终端服务设备视为需求节点,以路径损耗等有关距离的因素作为成本,目的是尽可能降低无人机部署的最大成本.

Wang等[52]提出了一种无人机节能部署算法,使用最小的传输功率服务一组地面用户,保证满足边缘用户的QoS要求.Noh等[53]通过调整天线半功率波束宽度、方向和三维部署位置,使边缘用户的路径损耗最小,获得无人机的覆盖范围.Zhang等[54]分析了两个快速无人机部署问题:一个是在考虑公平条件下,使所有无人机的最大部署延迟(min-max)最小;另一个是在考虑效率条件下,使总部署延迟(min-sum)最小化.

3.5 模型分析

通过对不同模型进行对比分析,得到表1.可以看出,MCLP和SCP的区别在于,前者是给定无人机数量,使覆盖范围最大,后者是给定覆盖范围,使无人机数量最少.MCLP模型能够在无人机资源有限情况下,充分利用资源,尽可能多地覆盖用户,但缺点是缺乏公平性.SCP模型则是以全覆盖为目标,并尽量减少成本,可以平衡覆盖水平与效益.p-median模型与pcenter模型之间的区别在于是使总成本还是最大成本最小.前者可以将设施建设的总成本降到最低,但遥远的需求节点需要更长的时间才能获得服务.后者尽可能考虑每个节点获得服务所需的时间,主要用于紧急救援活动中的无人机部署问题.通过统计主要文献使用的模型得到图1,发现69%的文献是覆盖问题,22%的文献是p-median问题,只有9%的问题是p-center问题.p-center模型能够考虑到距离设施较远的用户,具有良好的公平性,广泛应用于应急设施选址问题.但目前基于p-center模型建模的无人机基站部署研究相对较少,因此有待进一步扩展研究,探索其在应急事件中的建模应用.

图1 不同问题模型的主要文献分布Fig.1 Distribution of the main literatures on different problem models

表1 不同问题模型的对比分析Table 1 Comparative analysis of different models

根据本章分析,发现能量消耗是考虑较多的,但是当前研究主要通过降低发射功率实现节能,对于无人机的能量补充问题考虑的较少,因此可持续充电策略下的无人机基站部署是一个值得研究的重要方向.对于多无人机部署,关于无人机间的连通及干扰因素考虑也较多,但大多数研究却没有同时考虑连通和干扰,这进一步增加了建模难度.为更贴合实际,仍需进一步深入研究同时考虑连通和干扰下的无人机基站部署.关于用户分布,目前对于用户移动场景考虑较少,这是因为动态场景下的建模和求解更为复杂,因此实时动态部署无人机基站是未来的一个研究难点.在目前无人机基站部署的相关研究中,更多是独立地部署无人机基站,探索地面基站存在下的无人机基站部署是一个值得研究的现实问题.

4 算法

由于无人机可以在一定空域范围内任意位置悬停,无人机基站部署问题的解空间理论上是无限大的,因此对于无人机基站的部署优化问题,在求解时一般会对解空间进行一定简化或转化,然后再设计求解算法.经过多年研究,精确算法、近似算法、聚类算法、启发式算法、学习算法等都被尝试用来求解不同的无人机基站部署问题.

4.1 精确算法

精确算法在问题规模较小时能在可接受的时间范围内求解出问题最优解,在无人机基站的部署优化中使用较多的有穷举搜索、分支定界算法等.Kalantari等[37]使用穷举搜索和分支定界算法求解无人机基站部署问题.Cui等[47]使用一种迭代算法和一种穷举算法来优化无人机的位置,以覆盖随机分布的所有用户.

一些研究者将无人机基站放置问题建模为解析几何问题进行求解.Mozaffari等[25]推导出了无人机下行链路覆盖概率与海拔高度和天线增益的关系.利用圆包装理论,求解使无人机覆盖寿命最长的最佳三维位置.Alzenad等[14]在垂直和水平维度解耦了无人机的部署问题,首先找到最大覆盖区域的高度,再搜寻最佳二维平面位置.将无人机在水平维度上的部署转化为一个圆放置问题,并使用MOSEK求解;为降低发射功率,进一步引入一个最小覆盖圆问题,将其转化为二阶锥问题,使用CVX解析器进行求解.

Wang[52]等提出一种节能放置算法,令无人机用最小传输功率覆盖所有用户.首先将水平面的问题转化为最小覆盖圆问题,并建模为二阶锥问题使用MATLAB求解出最佳水平位置及最小覆盖半径.最后根据最优无人机高度与最小覆盖半径之间的线性关系,使用MATLAB获得最优高度.

除了将无人机部署问题转化为圆包装、圆放置、最小覆盖圆等问题,Mozaffari等[43]提出了基于截断八面体形状的无人机部署方法.截断的八面体是球体最近的近似,可以完全镶嵌在三维空间中,因此可以尽可能减少完全覆盖三维空间所需的多面体数量来优化无人机部署.Babu等[55]在无人机间的干扰和能耗条件下,解析地推导出了多无人机的全局最优节能高度,然后设计了一种新的基于多层规则多边形的无人机放置算法求解最优水平位置.

求解无人机基站部署问题的精确算法并不能保证得到无人机在连续三维空间的最优解,而是首先对部署问题在水平和垂直维度上进行解耦,然后分别求解精确解.

4.2 近似算法

近似算法是指设计算法得到的近似解,能够在数学证明该近似解与全局最优解相差A倍(A被称为近似系数),并且算法复杂度为多项式时间复杂度.Lyu等[3]提出了一种部署连续移动基站的多项式时间算法,这种算法在最坏的情况下具有多项式时间复杂度O(k3),远低于k均值聚类算法.

Zhang等[54]还研究了如何快速部署无人机网络实现最小最大部署延迟.对于最小最大部署延迟:当多无人机从同一位置出发时,设计了一种复杂度为O(n2)的算法进行求解:当多无人机从不同位置出发时,设计了带有相对误差的全多项式时间逼近方法.

凸优化的相关技术也常被用来近似求解无人机的部署优化问题.刘伯阳等[56]将无人机辅助移动边缘计算的位置部署和资源分配问题转化为非凸优化问题,并利用连续凸近似和二分法对其进行两阶段迭代求解.Chen等[57]提出了密集边界优先覆盖方案,其中设计了一个可行区域划分算法,通过拉格朗日乘子法将可行区域划分为内外可行区域,得到使单架无人机容量最大的最佳位置.

Wang等[58]首先提出了一种基于深度学习的预测方法分析长期历史照明分布的时间和空间特征,然后利用用户关联约束的物理松弛,将原始的非凸问题转换为凸等价问题,最后设计了一种对偶分解迭代算法,求解在照明、通信和用户关联约束下使总传输功率最小的无人机部署问题.Luo等[59]提出了一个两层优化策略优化无人机部署,上层基于动态规划的投标优化方法来优化用户分配,而下层则使用交替方向乘子法解决比特分配和无人机位置的动态变化.

近似算法将无法直接求解出精确解的复杂问题,经过数学近似或松弛求解,获得较优解.这种算法计算复杂度较高,更适用于小规模问题,不太适合求解大规模复杂性问题.

4.3 聚类算法

聚类算法主要用于优化无人机在水平面的位置,对服务的用户或设备进行聚类,然后将每个集群的中心作为无人机的水平位置,最后通过高度公式或者搜索算法等得到无人机的三维空间位置.Galkin等[60]采用k-means聚类来分别确定无人机基站的位置和用户关联.在给定用户坐标的情况下,根据欧几里德距离对用户进行聚类,然后将用户关联到无人机基站,并优化基站的位置.Zahedi等[48]应用模糊聚类算法来确定p-median部署问题中的一组初始候选点,再利用二分法得到p的最优值,最后通过CPLEX求解无人机天线的最优位置.Noh等[53]提出一种椭圆聚类算法求解无人机基站部署问题,目的是使用户覆盖概率最大,并以最小传输功率避免干扰.

考虑到空对地传播通道的特征、其他无人机同频干扰的影响以及无人机的能量约束,Hydher等[18]使用k-means聚类优化无人机的水平位置和用户分配,再利用搜索空间约束的穷举搜索和粒子群优化两种方法,寻找无人机的最优高度.Yang等[61]提出了一个主动的无人机部署框架,用于缓解快速人群流量下蜂窝网络的过载情况.首先设计一个联合时间空间的混合分布来描述用户分布,然后提出关于用户网络需求的预测方案,最后使用聚类方法确定所需无人机的数量和位置.

应用聚类算法得到的无人机基站部署方案一般只是一个局部近似优化解,还有进一步优化的空间.因此,一般使用聚类算法获取初始解.

4.4 启发式算法

启发式算法是求解无人机基站部署优化问题的常用算法,主要包括构造启发式算法和元启发式两大类.

4.4.1 构造启发式算法

构造启发式算法主要是针对无人机部署问题的特点,基于贪婪、节约、聚类等思想,设计构造可行解的规则,进行启发式搜索,得到问题的可行解,一般为局部最优解,少数情况可以得到最优解.Zhang等[62]提出一种自适应多无人机部署启发式算法,在热点区域迭代部署无人机基站,每次迭代部署一个可以为最大数量用户服务的无人机,直到满足所有用户的QoS要求,以确定最少的无人机数量及其经度、纬度和高度.

Wang等[63]建立了一种新型的多无人机移动边缘计算系统,包含无人机部署和任务调度两层优化问题.在上层使用带有贪婪消除算子的微分演化算法来优化无人机的部署,首先确定无人机的最大数量,再使用贪婪消除算子逐渐减少无人机,直到在满足各项约束条件下不能再减少为止,最后使用微分进化算法进一步优化剩余无人机的部署位置.

Sobouti等[49]设计了bi-section算法,用来求解无人机p-median的p值,并使用用户探索方法、简单网格划分和智能网格划分从候选节点中选出了p个最优位置.实验结果表明,这种方法能够有效减少搜索空间.

4.4.2 元启发式算法

元启发式算法通常具有通用的启发式搜索框架,通过迭代搜索不断优化解空间,不借助于某种问题的特有条件,能够广泛应用于求解大多数组合优化问题.应用不同元启发式算法的搜索框架求解无人机部署优化问题,可以简化求解过程,优化部署效率及效果.常用的元启发式方法有粒子群算法、遗传算法、灰狼优化及混合元启发式算法等.

1)粒子群算法

粒子群优化(particle swarm optimization,PSO)算法是模仿鸟类捕食行为的一种种群迭代搜索算法,是求解无人机基站部署问题的常用元启发式算法之一.Kalantari等[12]使用PSO算法求解无人机在容量约束条件下不同用户密度区域的位置,通过删除不影响网络质量的无人机基站来优化最终的部署数量和位置.Li等[64]应用PSO算法进行二维搜索,求解发射功率约束下无人机基站的最大覆盖问题.首先在二维平面上初始化粒子群的随机位置和速度,通过限制天线波束角和无人机飞行高度实现节能约束;然后以无人机的覆盖面积作为适应度函数进行迭代,最终达到迭代标准后停止.

Shi等[38]在每个无人机单元上独立地使用PSO算法,将每个无人机看作是一个粒子,以求解在保持D2B链接质量下的无人机部署问题.相较于将多无人机看作一个粒子的PSO算法,可以避免陷入局部最优.Arafat等[65]提出了一种基于PSO的无人机群智能三维定位算法,通过边界框的方法在有限边界内使用粒子进行搜索.李晓伟[66]提出了一个基于PSO的两阶段联合优化算法,分别优化无人机部署位置和循环充电策略,以实现高能效、可续航的多无人机协同覆盖服务.基于上一次迭代的最优循环充电策略,优化无人机部署位置;并使用离散PSO优化循环充电策略,目标均为使无人机系统的能源效率最大化.

2)遗传算法

遗传算法(genetic algorithm,GA)是一种模拟生物进化论的自然选择和遗传学机理的生物进化算法,也常用来求解无人机部署问题.Roberge等[26]在无人机部署中考虑了无人机最小燃料消耗和平均飞行高度等动态约束,提出在GPU上并行实现GA,与基本GA相比,使用大规模并行架构的GA执行时间减少了290倍.

Plachy等[4]设计了基于遗传算法的无人机部署优化算法,在传统GA基础上根据无人机基站部署问题的特点改进了选择算子、交叉算子和突变算子.选择算子使用轮盘赌方法,选择一个父代,使其适应度值大于一个0∼1间均匀分布的随机数w.交叉算子通过一个0∼1间均匀分布的参数α,对两个父代的位置进行更新.突变算子是以一定的概率随机选择一些个体在原有位置上增加一个向量,向量值由个体所在位置决定,方向随机确定.通过检查种群多样性选择下一代个体,如果多样性不够,使用一个更高的突变概率对父代进行突变,避免过早收敛.

王超[67]设计了改进遗传算法求解无人机部署问题.首先对无人机所在二维平面使用网格划分进行离散化处理,将无人机部署在网格中心,形成无人机的侯选位置集合.然后采取二进制编码方式表示每个位置是否部署无人机,侯选位置集合大小即为染色体基因编码的长度,编码中的每一位代表无人机的侯选位置.为避免无人机之间重复覆盖,提高种群多样性,他对标准遗传算法进行改进,在每一代进化操作之后对新种群中的染色体进行安全距离和部署约束的检查和修正.

多目标进化算法也常用来解决多目标无人机部署问题.Sabino等[68]应用NSGA-II找到无人机的最少数量和最优位置,与目标区域的地面节点形成连接,以满足用户的服务质量要求.Reina等[69]将覆盖、容错和冗余作为相关因素构建加权适应度函数,设计了多层次多子群遗传算法,优化多目标无人机部署,利用不同子群体随不同布局变化的特征,探索无人机网络在多目标覆盖问题中的应用.

3)灰狼优化算法

灰狼优化(grey wolf optimizer,GWO)算法是一种模拟自然界灰狼领导和狩猎机制的优化算法.芦方旭[70]基于平面搜索的灰狼优化算法,提出了改进灰狼优化算法,将无人机位置看作狼的位置,在三维空间内迭代搜索获得无人机的最优位置.首先划分灰狼的社会等级,将适应度最高的3个无人机位置看作是3个等级首领狼的位置,再进行跟踪包围,由3个等级首领狼带领其他狼搜索更优的位置,并重新选取适应度最好的3个位置标记为3个等级首领狼的位置,最后是攻击阶段,根据公式逐步逼近全局最优位置.

文献[71]设计了一种超启发式灰狼算法,通过迭代来逼近无人机最大覆盖要求下的纳什均衡点,实现最少无人机基站的最优部署.该算法应用近点搜索与远点搜索两类搜索空间扩大搜索;应用灰狼优化算法计算远点效用函数值,减少搜索空间、加快收敛速度;并且使用近点搜索和策略选择概率对纳什均衡点施加扰动,防止算法过早收敛.Ghazzai等[72]提出了一种LTE-Advanced规划方法,首先基于灰狼优化算法找到感兴趣区域中满足覆盖范围和容量限制的基站位置,并根据不同空间用户密度将该区域分为几个子区域,再使用迭代算法删除冗余基站得到一个可行方案.

4)混合元启发式算法

混合元启发式算法集成了两种或两种以上元启发式算法的优点,以提高搜索效率与效果.

向智睿[73]根据自适应差分进化算法和带惯性权重的粒子群算法的特点,提出基于自适应差分的人工蜂群算法.对传统人工蜂群算法的雇佣蜂阶段进行改进,首先引入惯性权重因子平衡算法的全局和局部搜索能力,再引入交叉率扩大搜索空间,最后通过差分向量和全局最好个体引导搜索解决蜜源搜索的随机性.

王福星[74]提出一种遗传粒子群算法求解多无人机覆盖部署问题,在粒子群算法更新个体速度和位置后,应用遗传算法的选择、交叉和变异操作产生染色体并加入种群,淘汰适应度低的染色体,以避免粒子群算法陷入局部极值.并且在基本交叉算子基础上,对基因的移动速度进行交叉,以赋予染色体速度应用到粒子群算法框架中.

涂慧[75]通过自适应惯性权重的遗传粒子群混合算法求解使网络中断概率最小的无人机部署问题.在传统粒子群优化算法基础上,为平衡搜索速度和精度,先根据粒子群的平均适应度值和最小适应度值,自适应得调整惯性权重,再更新粒子的速度和位置.并且为防止PSO陷入局部最优,扩大搜索空间,在应用PSO更新个体速度和位置后,使用遗传算法的选择、交叉和变异算子对粒子群进行再次更新.

5)其他元启发式算法

Li等[76]提出了基于无人机的人工蜂群算法(UAVartificial bee colony,U-ABC)求解受灾后无人机提供通信服务的部署问题.U-ABC与标准ABC的算法框架类似,它使用m个无人机基站的吞吐量之和构造新的适应度函数.在搜索过程中,将无人机看作蜜蜂,使用雇佣蜜蜂、观察蜜蜂和侦察蜜蜂3个算子,雇佣蜜蜂会根据当前解寻找更优解,如果搜索到的候选解优于当前解则被接受;观察蜜蜂使用轮盘赌方法选择新解,适应度越高越容易被选择;侦察蜜蜂用来跳出局部最优解.

向庭立等[77]首先在满足网络连通性约束下,估计需要的最少无人机数量以及热点区域范围,再基于标准布谷鸟算法提出了3处改进,首先根据热点区域信息对位置更新方程进行改进,然后根据当前鸟巢适应度值与最大适应度值对发现概率参数进行自适应改进,最后引入加权覆盖率对目标区域整体覆盖率和热点区域覆盖率进行归一化来改进目标函数,以重点优化热点区域的覆盖.

Islambouli等[78]设计了一种基于离子运动优化(ion motion optimization,IMO)的元启发式算法,迭代地搜索无人机的最优数量和位置以及设备关联和任务分配.IMO是一种基于种群的元启发式算法,其中候选解被表示为一半阴离子和一半阳离子.适应度函数由已部署的无人机数量和不满足约束条件的无人机和物联网设备数量构成,因此适应度函数值越低表示解的质量越好.

钟舒馨[79]针对无人机部署问题,提出了一种基于力平衡的启发式方法.根据无人机与用户间的距离及用户需求建立引力,无人机则根据引力大小自适应得部署到较优位置.她还提出了自适应区域划分方法,使得每个区域内用户数量近似相同,以提高无人机资源利用率.

王花[80]提出了基于3种相对距离的启发式方法解决无人机在灾害场景下的部署.首先将无人机随机部署在同一高度,并将部署区域离散化成大小相同的方格,无人机部署在方格中心,再基于无人机与未覆盖网格间的相对距离、无人机与无人机间的相对距离、无人机与障碍物边界间的相对距离这3种相对距离更新无人机的位置,以解决多无人机间覆盖重复和覆盖盲区问题.

启发式算法常用于求解组合优化问题,同样是求解无人机基站部署优化问题中最常用的方法.这是因为根据问题特点,设计构造式算法或者使用通用算法框架,相对来说更容易实现,并且能够获得更优解,平衡解的质量和求解速度.但是启发式算法不太适用于用户移动场景,可以开发启发式算法和学习算法相结合的新型算法用于实时在线部署无人机基站.

4.5 学习算法

随着人工智能技术的发展应用,探索机器学习类算法在无人机基站部署领域的应用成为近年来的一个新兴方向.

机器学习算法可以基于大量数据学习经验,训练模型进行行为预测.因此很多文章基于机器学习预测用户需求和分布,实现无人机基站的部署.Sharma等[2]提出一种基于神经元成本函数的多无人机部署方法.这个模型根据用户需求模式为每个无人机和区域分配一个成本和密度函数,再使用这些函数通过基于用户需求模式的反神经元模型为每个区域分配相应的无人机.Chen等[81]引入了一种新的基于概念或基于回波状态网络的学习算法来预测用户的内容请求分布和用户上下文的移动性模式,然后根据预测的用户行为找到用户–无人机的关联、无人机的最佳位置和内容缓存策略,使用户体验质量最大,传输功率最小.

Sharafeddine等[41]将三维离散搜索空间的问题表述为一个混合整数问题,提出了基于无监督学习技术的连续三维空间多无人机部署方法,使用排斥力和吸引力的静电概念,为无人机基站分配动态正电荷,为用户分配固定负电荷,这样在空中基站和用户之间,以及在空中基站之间会形成一个电场.空中基站和用户会在空间中不断移动,直到达到静电平衡,形成三维空间的固定位置.

任佳智等[82]首先使用基于线性回归的方法来预测用户将来发起内容请求时的位置和时间,再结合用户内容偏好,分别应用基于自组织映射神经网络的聚类算法和基于凝聚嵌套的分簇算法计算无人机的位置,并据此设计部署方案.El Hammouti等[83]提出了一种Learn-As-You-Fly算法,允许无人机动态地学习其最优的三维位置,并与地面用户进行关联,使网络和速率最大.通过分布式匹配方案解决无人机与用户的联系,并使用改进的k-means来更新无人机的二维位置,最后通过基于干扰的邻域结构优化局部效用函数来调整无人机的高度.

强化学习也是求解无人机基站部署优化问题的重要方法,通过不同的动作改变agent的状态,再通过奖励函数评价并反馈在不同状态下的不同动作,不断训练后最终生成较好的策略.Klaine等[36]提出一种使用Q-learning的分布式方法,每个无人机都是Q-learning的代理,无人机的状态被定义为环境中的三维位置.每个无人机根据ε-greedy策略选取7种可能行动中的任何一个进行移动,以找到覆盖用户数量尽可能多的最佳位置.

郜富晓[84]基于深度强化学习算法联合优化无人机的位置部署和能量消耗.通过获取无人机的状态信息,估计无人机下一步的移动动作及需要消耗的能量,并设置奖励函数对无人机移动的动作成本进行奖励或者惩罚,最终将无人机部署到最佳位置.

Ren等[85]采用深度强化学习来获得动态环境下大规模无人机接入移动边缘计算的实时调度策略,从而根据动态系统状态生成高效的无人机移动和任务卸载策略.周毅等[86]基于深度强化学习解决考虑能效优化的无人机部署问题,将无人机的初始位置和地面终端的分布作为状态集合,将无人机的能效作为奖励函数,根据DNN和Q-learning指导无人机的动作,以找到满足覆盖率和路径损耗下能耗最小的位置.

学习算法具有良好的学习性能,可以实时学习用户状态和需求,进而在线部署无人机,常用于求解连续动态空间的无人机基站三维部署问题,具有较好的研究前景.但算法设计中随机性较强,对于强化学习方法如何设计“动作”非常关键.

4.6 其他方法

除了以上常用的方法外,还有一些研究者采用控制算法和博弈论等方法求解无人机基站的部署优化问题.

Zhao等[20]将无人机部署的SCP问题看作持续编程问题,并设计基于虚拟力的分布式运动控制算法进行求解.在每次迭代中,无人机根据4种虚拟力(热点区域的吸引力、用户的吸引力、防碰撞的排斥力、防障碍物的排斥力)形成的合力的方向和大小飞行到合适的位置.当合力小于阈值且无人机实现双连接时,结束迭代过程.吴炜钰等[87]基于虚拟力求解双连接无人机网络的按需覆盖部署问题时,引入了最大移动距离对虚拟力合力进行归一化处理.最大移动距离会随迭代次数增加而减少,当所有无人机实际移动距离小于给定停止距离时,完成部署工作.Huang等[88]提出了一种反应式无碰撞三维部署算法,使用垂直和水平两个维度的导航规律来实现无人机的自主导航.

Ruan等[15]提出一种基于节能通信的无人机覆盖模型.这个模型被分为覆盖最大化和功率控制两个部分,都被证明是精确的势博弈并具有纳什均衡点.因此,他们基于博弈论框架设计了一种基于空间自适应行动的多无人机节能覆盖部署算法.Xu等[89]使用博弈论解决考虑用户具有双偏好情况下无人机基站在三维空间中的部署问题.双偏好是指用户可能会向无人机错误地报告他们的位置和偏好类型(有利的或不利的),以防止无人机远离它.

4.7 算法对比

根据图2文献统计,可以看到,精确算法、近似算法和聚类算法使用的频率相差不大,相对都比较低,学习算法因为其良好的学习性能,相关研究应用相对较多.而常用于求解组合优化问题的启发式算法占到了50%的比例,是求解无人机基站部署优化问题中最常用的方法.各类算法在求解无人机基站部署问题时都有一定的优势和局限性,表2对此进行了具体的对比分析.

图2 主要求解方法的文献分布Fig.2 Literatures distribution of the main solution methods

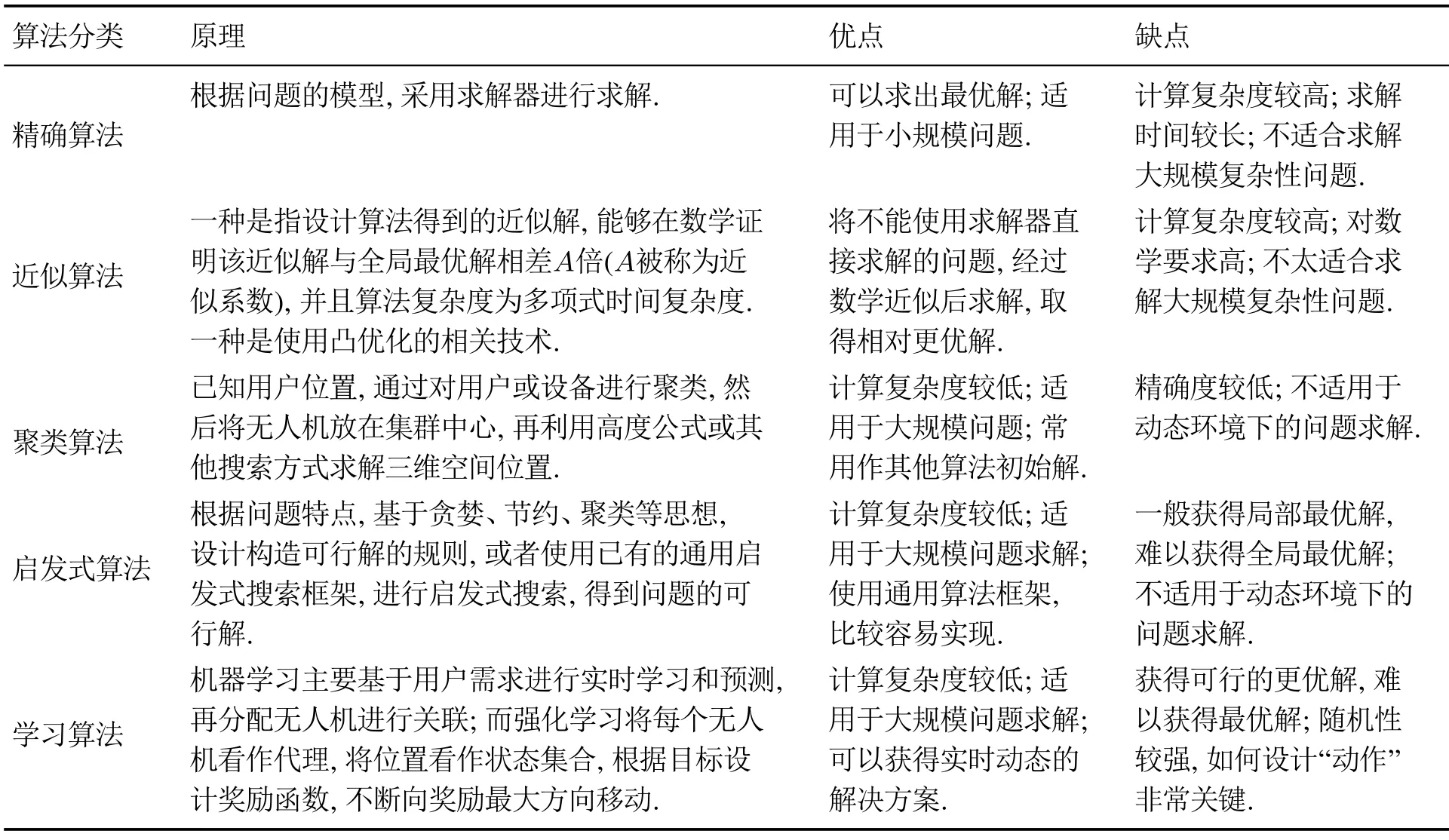
表2 不同求解算法的对比分析Table 2 Comparative analysis of different algorithms

5 实验

本章节主要对无人机基站部署问题的数据来源和典型数据集进行分析.

5.1 数据来源

实际应用中,用户一般在一定区域内随机分布,因此大多数无人机基站部署优化的实验数据集都是采用随机生成数据来模拟用户分布,即基于特定分布函数在一定区域内随机生成一定数量的用户位置.典型的用户分布包括随机分布[52]、泊松分布[62]、具有标准截断偏差的高斯分布[90]等.也有一些研究基于实际场景数据,Zahedi等[48]根据真实数据模拟点的分布.此外,基于真实地理数据的社交软件“陌陌”记录的数据,也能反映实际用户的分布情况,Huang等[16]基于“陌陌”选择中国北京1000×1000 m2的用户数据.表3对主要数据生成方式的代表性文献进行了总结.

表3 主要数据来源的代表性文献Table 3 Representative literatures on primary data sources

5.2 典型数据集

无人机基站部署问题的模型构建及算法设计是否有效,需要通过实际案例数据或现有算例数据来验证.由于真实案例数据具有难以收集、通用性较弱等问题,很多研究者通过随机生成测试数据来开展研究.在无人机基站的部署问题中,数据构造需要考虑部署环境、区域范围及高度限制、用户规模及分布等参数.关于该问题的研究时间较短,因此目前国内外还没有统一的测试数据集.表4总结了典型测试用例的代表性文献,为研究无人机基站的部署问题提供参考.

表4 无人机基站部署问题的典型数据集Table 4 Typical dataset of the UAV base station deployment issues

6 未来研究展望

无人机基站的部署优化作为一个新兴领域,目前已有不少研究致力于如何建立模型和设计算法,但根据上述综述,这个领域的研究还可以进一步发展应用.从当前问题特点、建模方法、求解算法和实验应用的研究现状来看,无人机基站部署优化领域未来的拓展与深化方向包括以下几个方面.

从无人机基站部署问题的特点来看:1)优化可持续充电策略下的无人机基站部署是未来一个重要研究方向.当前研究对于部署高度、能量消耗等因素的考虑较多,而对于无人机的能量补充问题考虑的较少.小型无人机续航能力低是限制无人机应用的重要因素,目前大部分研究考虑如何优化部署来降低功率损失,对于充电策略研究较少,未来探索部署过程中无人机的循环充电策略是一个重要研究课题;2)同时考虑连通性和干扰,优化无人机网络的部署.在部署多无人机形成无人机网络时,为了简化问题,大多数研究更侧重于无人机间的连通性,没有考虑同频带传输下的干扰.但实际情况下,无人机间的连通性和干扰会分别影响无人机网络稳健性和网络质量,因此同时考虑连通性和干扰、优化无人机基站部署是一个重要研究方向;3)优化动态环境下的无人机基站部署.目前大部分研究集中在确定环境下的无人机基站部署,对于用户位置的动态性、环境干扰的不确定性等考虑的较少,后续融合动态不确定性因素的研究是该领域的一个难点;4)优化地面基站存在下的无人机基站部署.目前关于无人机基站部署问题的研究,更多是独立地部署无人机基站.如果存在多个地面基站,在部分地面基站损毁或容量不足时,如何灵活部署无人机基站、保持与其他地面基站的连接以满足用户需求,是一个值得研究的实际问题.

从无人机基站部署问题的建模方法来看:1)如何建模将连续解空间转换为离散解空间? 单架无人机的部署一般采用解析方法,而多架无人机的部署一般都需要进行解空间离散化,然后采用整数规划方法,借鉴经典设施选址模型,建立无人机部署的优化模型.但是解空间的离散化过程还缺乏规范的方法或指导框架,大多需要决策者根据实际情况辅助完成.因此,建立无人机部署优化问题的统一建模框架,指导从连续解空间向离散解空间转换,能够提高数学规划建模的效率;2)如何建模使离散解空间回归连续解空间?基于整数规划的模型得到的解并不能保证是连续空间内的最优解,进一步研究如何在整数规划模型求解的基础上回归连续解空间,进而得到更优的部署方案,也是建模领域的重要研究方向;3)探索p-center模型的扩展使用.据文献统计,目前大部分研究基于覆盖模型或p-median模型进行建模,对于p-center模型的探索使用较少.未来可以发挥p-center模型的公平性优势,探索其在紧急救援情况下无人机部署问题的建模应用.

在无人机基站部署的优化算法方面:1)探索设计混合优化算法.早期研究以精确算法和聚类算法为主,随着问题规模不断变大,对求解性能要求越来越高,各种元启发式算法应用越来越广泛.当无人机基站部署问题越来越关注各种环境影响因素,问题复杂性迅速增加.将问题进行分解,集成多种启发式算法的优势联合解决无人机基站部署问题是混合优化算法的主要设计思路;2)探索知识和数据协同驱动的优化算法.当前算法中知识驱动的优化算法应用较多,同时,近些年开始探索机器学习这类数据驱动算法的应用,常用于求解连续动态环境下的无人机基站部署问题.未来进一步研究知识和数据协同驱动的优化算法,充分集成无人机基站部署的领域知识,可以提高问题的求解效率,实现在线动态的部署规划;3)加强算法对比分析.目前关于无人机基站部署问题,大多数研究比较侧重探索设计算法,但是和已有算法的对比分析相对较少,建议在未来研究中加强算法的对比分析.这样有助于促进该领域算法研究的不断进步和更新.

在实验验证与应用方面:1)开发标准测试用例.目前大部分的研究采用随机生成算例,缺乏统一的标准测试用例.而标准测试用例的开发对于无人机基站部署优化问题的模型和算法有效性的验证至关重要,因此有待进一步开发和完善;2)基于数据挖掘技术,获取真实案例数据.采用真实数据进行实验验证的文献相对较少,随着数据挖掘技术的发展,数据获取的方式越来越多样化,未来可以探索更多数据采集方式收集真实数据,更充分地测试问题模型和求解算法的实际应用性能,使得研究更具有实际意义.

7 小结

随着自控技术、信息技术和人工智能技术不断发展进步,无人机开始广泛应用于军事和民用领域,其中通过部署无人机基站快速构建局部无线传感网、为用户提供应急服务是小型无人机的重要应用领域之一.无人机基站部署优化问题的建模与优化算法一直是该领域的研究重点与难点.通过优化无人机部署在空间的位置,可以减少应用成本,并且提高服务效率、质量等.论文总结了无人机基站部署的影响因素,分析了基于不同选址模型的无人机基站部署建模,阐述了不同求解算法的优势和局限性,归纳了实验的数据特点,展望了无人机基站部署的未来研究方向,可以为相关学者开展该领域的研究提供有价值的参考.