基于多分支残差深层网络的稀土萃取流程模拟
朱建勇,王 伟,杨辉,徐芳萍,陆荣秀
(华东交通大学电气与自动化工程学院,江西南昌 330013;江西省先进控制与优化重点实验室,江西南昌 330013)
1 引言
自20世纪70年代徐光宪教授提出“串级萃取理论”以来,我国稀土萃取分离技术逐渐处于国际领先水平,其团队后续发表的串级萃取静态计算和动态模拟方法进一步为稀土萃取工艺提供了优化指导[1].目前,基于串级萃取工艺的实际生产过程存在分离级数多、相邻级间变化缓慢以及多变量、非线性和强耦合等特点[2],生产过程中常依赖人工经验调整参数,限制了企业产能.为了提高工业智能化水平,根据生产工艺参数对稀土萃取过程预先进行流程模拟,预测可能的萃取状态,从而为后续的流程重组和工艺调整提供决策依据,这对于避免人工经验的主观性和提升生产效率具有重要意义[3].王振华[4]针对基础串级萃取理论不匹配多组分萃取体系的问题,提出“等效组分、等效分离因素法”将多组分体系简化为两组分进行计算,并通过计算机仿真模拟了串级萃取操作.但是因为料液中元素占比不均衡,对于远离切割线的元素,该方法计算出的等效分离系数偏大.钟学明[5]提出平均分数法求取多组分稀土萃取体系中不同元素组分间的有效分离系数,进而模拟出各级组分含量变化,当难萃和易萃组分间摩尔分数相差较大时,该方法计算精度会下降.此后,文献[6]提出相对分离系数静态计算模型,并设计仿真软件计算各级组分含量与出口组分含量值,但该算法未考虑萃取效率的变化,计算值与实际值间存在偏差.文献[7–8]通过简化热力学平衡模型搭建出多组分稀土萃取流程模拟器,用于计算萃取过程的元素平衡浓度,该方法基于简化的机理分析,忽略实际特性,也不能准确描述实际生产过程.
由于稀土萃取过程中伴随着复杂的物理化学变化,目前仍有部分机理不明[9].在未能完全掌握萃取机理情况下,构建的机理模型不能准确表达实际萃取过程中的组分含量变化.随着深度学习技术的蓬勃发展[10],如神经网络等数据驱动方法[11]开始被用于研究稀土萃取流程建模问题.Giles等[12]较早利用人工神经网络模拟各种稀土萃取体系中的物料传递过程,其对组分含量变化的预测结果比传统模型更准确.文献[13]介绍了反向传播神经网络在稀土溶剂萃取平衡数据模拟中的应用,其采用神经网络模型预测有机相和水相元素分配比的误差是常规模型的四分之一.但是,对于存在工况频繁变化的复杂工业过程,浅层神经网络的学习能力不足[10],不能满足复杂长流程模拟精度的要求.此外,稀土串级萃取工艺具有萃取级数多、级间耦合性强等特点,而LS-SVM[14]、ANN[15]作为黑箱模型,预测结果统一在最后的网络输出层显示,也不符合组分含量层次化输出的稀土萃取流程.
针对传统前馈神经网络不能很好地表达多级输出的问题,有学者改进了卷积神经网络(convolutional neural networks,CNN),提出一种多分支神经网络结构[16–19]应用于需要逐级输出预测结果的场景.分支神经网络的概念较早出现在文献[16],该文提出一种称为BranchyNet的新型网络结构,通过在传统CNN结构上增加额外的侧枝分类器,使得具有不同置信度的预测结果从不同分支输出,降低了计算冗余度.此后,文献[17]提出了一种多分支神经网络(multi-branch network,MB-Net),用于解决不同遥感场景图片数据集手工标注存在差别的知识自适应问题.文献[18]提出一种新的多特征分支卷积神经网络(multi-feature branch based CNN,MFB-CNN),用于心电图识别问题中对心肌梗死情况的自动检测和定位.文献[19]提出一种可端到端训练的两分支划分与重组网络,用于完成车辆重识别任务,仿真结果表明不用依赖额外注释就达到比现有方法更高的准确性.通过对网络结构的改进,上述多分支网络在图像分类[20–21]、事件识别[22]等分类问题上取得了较好的效果.稀土萃取流程模拟[23]是根据原料液属性、添加药剂量等生产条件参数建立流程模型以预测目标萃取槽的元素组分含量值(工艺指标),本质上属于多输出回归问题[24].作者目前还未发现多分支神经网络应用于类似多输出回归领域的工作.
针对稀土萃取过程存在的实际特性,本文在多分支神经网络结构基础上,创新性地提出一种多分支残差深层网络方法(multi-branch residual deep network,MB-RDN)应用于稀土萃取流程模拟.MB-RDN在其分支输出中引入残差结构[25]以及特征短接操作[26]实现多层次特征融合,使得MB-RDN不仅拥有深层神经网络的强大学习能力和分支神经网络的逐级输出特性,还可以有效缓解梯度消失问题.此外,本文根据分支网络的结构特点,设计了对应的多分支深层网络训练策略(multi-branch deep network training strategy,MBTS)用于模型训练.仿真结果证明了所提方法对于稀土萃取流程模拟问题的有效性.
2 工艺描述及多分支神经网络
2.1 萃取分离工艺描述
由于稀土元素间分离过程缓慢,稀土工业常将一定数量的萃取槽级联,使得原料液在洗涤剂和萃取剂作用下可以在各级萃取槽中连续混合–搅拌–分离–澄清,以此提纯目标稀土元素[13].图1描述了稀土串级萃取分离工艺流程,该流程分为n级萃取段和m级洗涤段.处理后的原料液从第n级加入,通过电机搅拌和分离,易萃组分会逐渐分布到每级萃取槽的上层(有机相),难萃组分逐渐沉淀到每级萃取槽的下层(水相).上层有机相溶液从左向右流动,下层水相溶液从右向左流动.经过该工艺,即可从第1级萃取槽获得组分含量为YB的难萃产品,在第n+m级获得组分含量为YA的易萃产品.由图1中所示,第i级需要观测的组分含量值为y(i)=[yi1yi2],i∈[1,j],其中yi1表示第i级萃取槽中易萃组分(有机相)含量值,yi2表示第i级难萃组分(水相)含量值,总级数j=n+m.
针对图1中描述的稀土萃取反应过程,使用简单的浅层网络即可模拟前几级萃取槽中的组分含量变化.但随着流程级数的增加,其内部复杂度也不断增加,故需要更深的网络结构表达组分含量变化与工艺参数间的关系.当级数较少时,如果采用与数量级大的萃取级相同的深层网络,又会因其复杂度不足导致模型过拟合.传统前馈神经网络无法满足稀土萃取过程对网络深度的要求.故本文首先设计一种基础的多分支深层神经网络(multi-branch deep neural network,MB-DNN),通过逐级引入分支输出初步解决了此问题.

图1 稀土萃取分离工艺示例Fig.1 Schematic diagram of rare earth extraction and separation process
2.2 多分支深层神经网络(MB-DNN)
MB-DNN基本结构如图2所示,其由主网络、分支层和输出层组成.MB-DNN采用多隐含层结构逐级学习原始特征,并在主网络下引入n+m级独立分支bi,i∈[1,n+m],每个分支包含相应的输出,使模型能够充分学习到输入输出间的复杂映射关系.相比单向输出的前馈网络,多分支网络结构考虑了工业过程中不同输出与输入特征间映射复杂度不一致的实际特性,避免了建立多个不同深度网络模型的冗余和设备计算压力.

图2 MB-DNN基本结构Fig.2 Basic structure of MB-DNN
对于一个具有n级萃取段和m级洗涤段的工艺流程,设计的MB-DNN具有n+m个分支,每个分支末端增加一个回归层用于组分含量预测,由此可在输出层得到相应级数下的组分含量值.稀土萃取过程中,自第一级萃取剂进入料液开始反应至第n+m级有机相组分出口,各级萃取槽组分含量值与工艺参数间的复杂度关系逐级递增,且各萃取级间的组分含量变化具有耦合关系.基于此先验信息,MB-DNN在主网络中按实际反应顺序引出网络分支,使得后序分支可以提取前一级分支学习到的主网络隐含特征.假设输入共有p个特征参数,则建立的MB-DNN模型数学描述如下:
式中:y(j)=[yj1yj2],j∈[1,n+m]表示网络分支j对应的易萃组分与难萃组分输出;fj(·),j∈[1,n+m]为模型要学习的各分支输出函数.考虑神经网络中特征传递过程,可以将第j分支输出进一步表示为
3 多分支残差深层网络(MB-RDN)
实际的稀土萃取流程常常包含几十上百级萃取槽,如果MB-DNN网络分支随级数增加,其隐含层数也不断增加.原始特征经过逐层传递后存在梯度消失的风险[27],且当模型复杂度不断增加,网络会达到性能饱和.对此,本文利用残差结构能够同时学习深层特征和浅层特征的特性,在MB-DNN基础上再提出一种基于多特征融合的多分支残差深层网络(MB-RDN).
3.1 MB-RDN的结构设计
在MB-DNN结构基础上引入残差块进行改进,以分支j举例.在残差结构中加入特征筛选函数对输入特征X与分支j实际输出Yj间进行相关性分析,获取特征子集Xj,再通过残差块将Xj传递到分支融合层,由此可挑选出相关性更大的特征辅助预测.为使筛选的特征保留原始特征的可解释信息,本文采用决策树回归算法[28]作为特征筛选函数,表示如下:
式中:(X,Y)={(x1,y1),(x2,y2),···,(xN,yN)},其中:表示输入特征数据,yi,i∈[1,N]表示实际输出,N为样本量.决策树通过启发式方法划分特征空间,每次划分都逐一考察当前集合中所有特征的可能取值,再根据平方误差最小化准则选择其中最优的取值作为切分点.例如将第j个特征变量x(j)和它的取值s作为切分变量和切分点,并定义两个区域R1(j,s)=及R2(j,s)=,为找出最优的j和s,需求解下式:
式中:c1,c2表示划分后的输出值,括号内两个min意为使用最优的c1和c2使得各自区域内平方误差最小.找到最优的切分点(j,s)后,依次将输入空间划分为两个区域,接着对每个区域重复上述划分过程,直至满足停止条件,通过不断地迭代便可以生成最终的决策树.最后,可以根据对输出值的贡献度大小将所有特征进行重要度排序,以此筛选出特征子集.
图3所示为分支j的残差结构示意图,可以看出原始特征通过特征筛选后被跳跃连接到分支j的特征融合层,融合层再将Xj与主网络隐含层提取的抽象特征进行融合.融合特征随即被传递到后续的分支输出层进行组分含量预测.此时分支j可以同时提取到原始特征以及深层抽象特征.绿色方框表示分支j的输出层,其输入特征可表示为
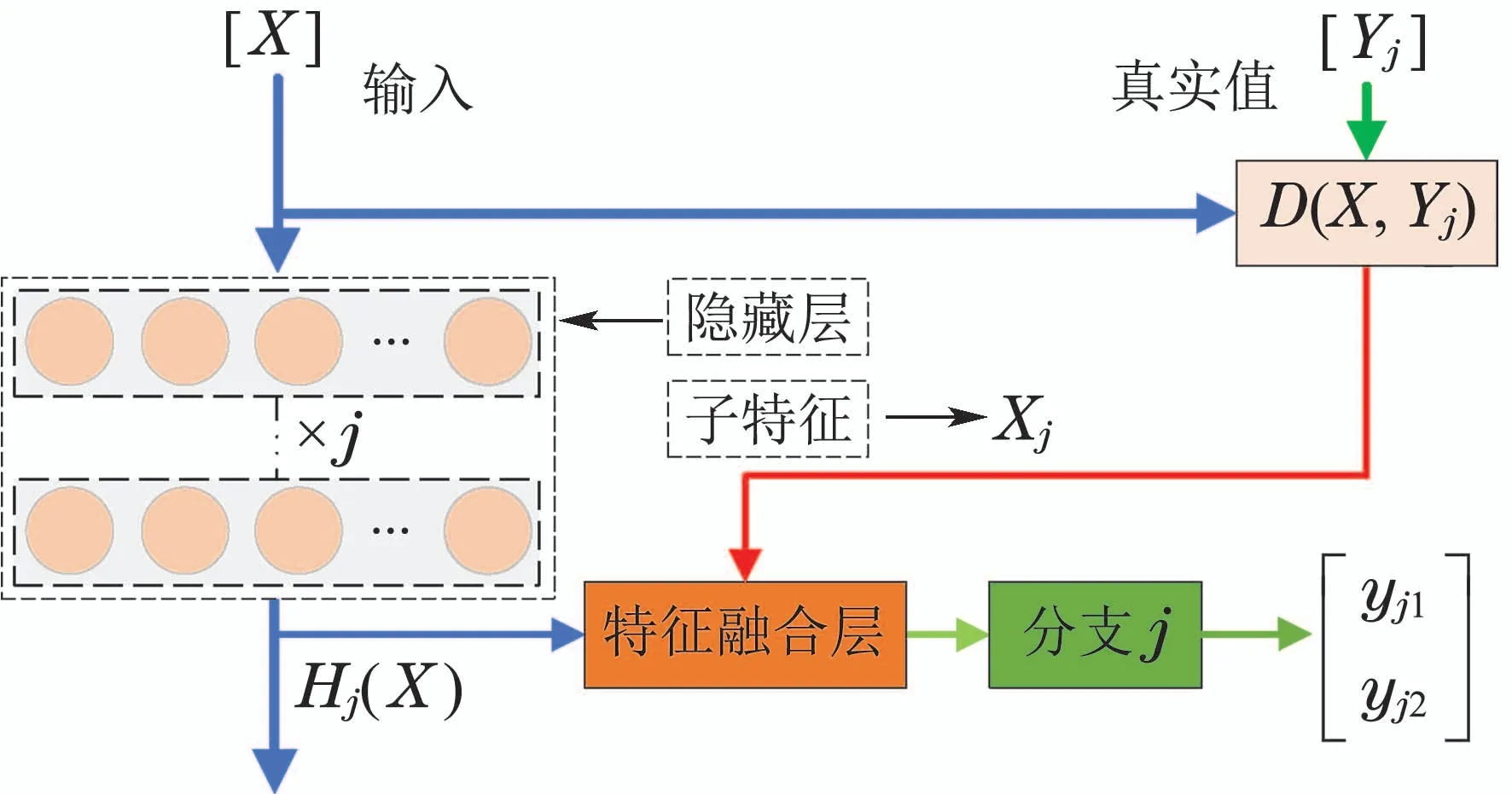
图3 基础残差块Fig.3 Basic residual block
式中:hBj表示分支j输出层的输入特征;Xj表示筛选出的子特征;Hj(X)表示主网络向分支j特征融合层传递的隐含层残差映射;⊕表示特征拼接操作,假设Hj(X)和Xj维度分别为dH及dX,则特征拼接后得到的融合特征维度dim[hBj]=dH+dX.
完整的MB-RDN结构如图4所示.针对萃取槽逐级串接的稀土萃取过程,考虑到相邻输出间存在的正向耦合作用,对分支1之后的n+m−1级分支再提出特征短接操作,使得前一级分支提取到的预测特征通过短接回路[25]被连接到后一级分支的融合层,作为相邻分支间的耦合特征进行学习.则通过原始特征筛选连接以及分支特征短接操作后,各分支能充分提取到数据原始特征、深层特征以及分支间耦合特征,使得MB-RDN可以利用包含多层次信息的融合特征对萃取槽中的组分含量变化进行预测.实现多层次特征融合后,分支j输出层的输入特征可由表示为

图4 MB-RDN结构示意图Fig.4 Schematic diagram of MB-RDN structure
式中:hB(j−1)表示前一分支输出层的输入特征.
以分支j举例,假设希望其学习到关于输入的理想函数为Oj(X),而f(X)是实际拟合出的函数,则有f(Hj−1(X))=Hj(X).对基本的MB-DNN,令其第j−1到第j隐含层中权重连接矩阵为Wj−1(忽略偏差项),则网络在训练中需要不断通过梯度更新来使得f(Hj−1(X),Wj−1)=Hj(X)=Oj(X).当引入残差连接Xj后,实际拟合的函数将会变为,Wj−1)=f(Hj−1(X),Wj−1)−Xj.而针对MB-RDN的多特征融合机制,即除了原始特征筛选外再引入分支特征短接,使得网络学习目标变为令⊕符 号表示特征融合.为了便于说明,暂时忽略分支输出层中的参数,只考虑其之前的传递过程.假设总共有L个分支输出,在主网络中每经过一个隐含层便形成一个分支残差结构,序号表示为j,每个分支输出的输入为hBj,j∈[1,L],那么有
令Ej表示MB-RDN中分支j在训练过程中的总误差,则反向传播公式为
可以看出,当增加多特征融合机制后,梯度计算公式中会存在常数项1.此时即便公式括号内右边项计算结果为0,依然可以保证梯度计算值不会太低,梯度消失问题将得到缓解.类似的特征重用机制[26]已被证明可以缓解神经网络层数增加导致的梯度消失和过拟合问题.
3.2 多分支深层网络训练策略(MBTS)
针对MB-RDN模型的训练,考虑其分支结构不同于传统的前馈型网络.本文针对性地提出一种多分支深层网络训练策略(MBTS)用于模型参数的更新.首先,对MB-RDN的n+m级分支建立独立的优化目标函数,本文采用均方误差(mean square error,MSE),得到各分支输出的损失优化函数如式(12)所示:
对于网络参数更新,MBTS提出隐含层逐级更新方法.即先确定第一隐含层以及其所连接的分支参数,再在该层基础上逐级训练得到更深层的参数,使得各分支输出能够描述实际萃取过程.基于先验信息,令前一分支学习到的网络参数作为后序分支的共同特征,符合稀土萃取逐级反应的实际特性.MBTS具体训练步骤如表1中所示.

表1 MBTS具体训练步骤Table 1 Complete training steps of MBTS
MBTS采用Adam算法[10]更新网络参数.Adam可以在消耗较少计算资源的情况下计算不同参数的适应性,加速收敛过程,该算法更新参数过程可以表示如下:
式中:δW和δB分别表示损失函数关于权重和偏差的梯度值;vw和vb是权重和偏差梯度的一阶动量;sw和sb是权重和偏差梯度的二阶动量;β1和β2表示指数衰减率,本文取默认值0.9和0.999.通过式(13)–(16)即可分别求得网络权重和偏差的一阶、二阶动量值,然后再进行如下计算:
网络中的神经元权重和偏差
式中:W和B分别表示网络各隐含层的权重参数和偏差系数;ε是一个用于保证数值稳定性的微小常数,本文取默认值为10−8;α表示学习步长,取默认值为0.001.Adam算法通过求解历史梯度的一阶动量和二阶动量动态更新网络参数,直至损失函数收敛至阈值即停止更新.
4 仿真结果及分析
4.1 数据集描述
以江西省某稀土公司一段具有60级萃取槽的LaCe/PrNd分离生产线作为研究对象.工艺流程如图1所示,其中镨(Pr),钕(Nd)元素合称为易萃组分(有机相),镧(La),铈(Ce)元素称为难萃组分(水相).对于实际生产线,现场技术人员只需要根据几个监测级中的组分变化趋势来进行工艺调整.因此,考虑到数据采集的成本,每组样本也只收集这几个具有敏感性和代表性的监测级组分含量作为标签数据.过程中实际组分含量的获取是通过手工提取5 个监测级(第15/25/30/35/45级)萃取槽溶液并进行离线分析.经过前期数据采集以及预处理,共获取到2000例样本作为原始数据集.为兼顾深层网络的训练效果,按8:1:1的比例将其划分为训练集、验证集和测试集.本文仿真平台是一台CPU为i5-9500K,内存8 GB的计算机,所有模型都是基于Tensorflow深度学习框架编程实现.
数据集中包含原料液属性、进料方式、药剂量等14个工艺输入变量以及相应萃取槽的组分含量.输入变量描述见表2中所示.特征X1–X4分别表示原料液中La,Ce,Pr,Nd 4种待分离元素的含量占比.不同稀土元素间具有不同分离系数,特征X5–X7分别表示相邻元素间的分离系数,如X5即表示Ce相对La元素的分离系数.变量X8和X9分别表示工艺中设置的主产品出口方式和原料液进料方式,本文将其离散化表示.对于X8,归一化后的数值0表示易萃组分为主产品,数值0.5表示难萃组分为主产品,数值1表示两者均为主产品.对于X9,0表示采用水相进料方式,1表示有机相进料方式.变量X10和X11表示注入的萃取剂以及洗涤剂使用量,不同的药剂量会影响到最终的稳态反应结果.变量X12表示原料液进料级数,设置不同的进料级会形成不同的萃取段和洗涤段.变量X13和X14表示萃取流程两端出口生产指标,由设计人员预先拟定,其中X13表示有机相产品出口分数(即输出料液中易萃组分的占比),X14表示水相产品出口分数.绘制测试数据集中输入变量以及第30级对应的易萃组分含量数据分布趋势如图5所示,不同特征间分布差异较大,无明显规律.

图5 输入变量与输出y(30)1数据趋势图Fig.5 The data trend of input variables and output y(30)1

表2 输入变量描述Table 2 Description of input variables
4.2 实验设置
本文选取平均绝对误差(MAE),均方根误差(RMSE)以及决定系数(R2)作为模型评价指标,计算公式如下:
式中:T表示样本总数;yi表示样本实际值;为模型预测值;ymean表示对样本输出实际值求平均.对于MAE和RMSE指标来说,其数值越小表明模型预测精度越高,而针对R2指标,其值越接近于1表示模型输出与真实值越接近.
基于需要模拟输出的5个萃取级,首先构建具有5个分支输出的MB-DNN和MB-RDN模型.受限于数据集规模,为了最大化验证模型效果,本文将两模型的主网络都确定为5 隐含层结构.在模型主网络中每两个隐含层后再引入批归一化[27]进行正则化操作,称为BN层.采用网格搜索确定隐含层中神经元的数量,MB-DNN 神经元个数在[32,40,48,56,64,72,80]范围内的性能变化如图6所示.
图6显示当神经元数量为64时,模型可以取得最好的性能.因此,本文设置MB-DNN和MB-RDN主网络中的神经元个数为64,则两者主网络结构表示为[14-64-64-BN-64-64-BN-64].同理,网格交叉验证后,两者分支末端的输出层神经元数量设定为32,其结构为[32-2].对于MB-RDN分支中的特征筛选操作,通过决策树算法进行相关性分析并根据贡献度大小将各特征进行排序,最后挑选对各分支输出贡献最高的前八个特征作为筛选特征引入对应的分支特征融合层.经过特征筛选后各分支连接的特征子集见表3中所示.

表3 分支特征筛选结果Table 3 Selection results of branch features

图6 神经元个数网格搜索Fig.6 Grid search for the number of neurons
由引文中所述,现有的多分支网络方法都是卷积神经网络针对图像领域的创新,并不能直接应用于稀土萃取流程建模.故将所构建的MB-DNN网络作为多分支残差深层网络(MB-RDN)的一种基础结构进行对比验证.为了充分验证所提方法的性能,再选择4种常见的数据驱动模型作为比较方法,分别是单输出的支持向量机、BP网络[13]、多层神经网络[15]以及具有时间序列记忆特性的长短时记忆网络[29].针对本文应用问题对各方法进行相应的设置.支持向量回归机(SVR)核函数采用多项式核函数,其他超参数基于交叉验证选取较优值.BP神经网络(BPNN)是单隐含层结构,其结构设置为[14-64-10].多层神经网络结构与MB-RDN的主网络设置完全一致,只是在最后直接添加输出层,结构为[14-64-64-BN-64-64-BN-64-10],称为5L-DNN.对于长短时记忆网络,将其堆叠为双层结构,神经元个数为64,时间步长设置为1,并在最后添加一个10输出的全连接层,表示为2L-LSTM.
各神经网络模型的激活函数统一设定为Tanh函数,训练周期设置为500,初始学习率为0.001,较大的训练周期是为了便于后续关于计算负荷的讨论.对比的神经网络方法使用基本的Adam算法进行训练,MB-DNN和MB-RDN则采用第3.2节提出的MBTS算法进行训练.小批量训练单次输入的样本量为32,设置学习率衰减系数为0.1,当损失函数在验证集上连续20 个周期没有明显下降时启动学习率衰减.训练结束后取验证集上的最优模型作为测试模型.
4.3 结果分析
训练结束后,首先验证所用数据集是否足以训练具有5层结构的深度网络,绘制关于5L-DNN,MBDNN和MB-RDN 3个深层模型的损失变化曲线,如图7所示.由图中结果可以看出,3个模型都能够在有限的迭代周期内达到收敛状态,证明训练是有效的.进一步观察发现,本文针对稀土萃取过程实际特点所设计的多分支网络相比传统的多层神经网络(5LDNN)收敛性能更好,多分支结构可以加速学习过程.特别是MB-RDN,在3个模型中具有最低的训练初始值以及最快的收敛速度.这结果说明基于多层次特征融合机制设计的多分支残差深层网络适合应用于稀土萃取流程建模.
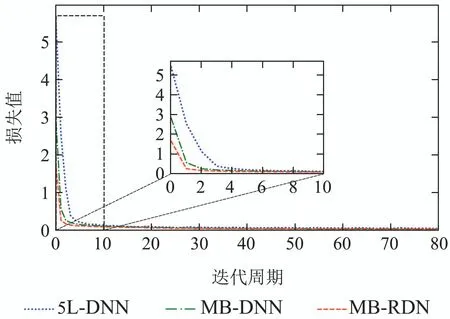
图7 损失函数变化曲线Fig.7 The change curve of the loss function
不同方法的测试评价指标对比如图8–10所示,区分了有机相和水相的结果.由图中结果可以看出,SVR和BPNN两个浅层方法可以较好地预测排序靠前的萃取槽中组分含量,但是对于更后序的萃取槽,由于反应复杂度的递增,导致两者性能有所下降,整体表现弱于5L-DNN.长短时记忆网络基于门控机制对于时序数据有较好的预测性能,但是本文中的2LLSTM对不同萃取级预测误差波动较大,分析是因为其只考虑到单一特征的时序变化,未利用数据中萃取级间的耦合信息,导致存在输出不平衡现象.具有多分支结构的MB-DNN和MB-RDN表现较优,其中MBRDN基于深层特征融合,并通过不同分支逐级输出预测值,可以稳定预测组分含量变化,预测精度总体优于5种对比方法.

图8 不同方法的MAE指标对比Fig.8 Comparison for MAE indicators of different methods
为了更加精确地比较不同方法的性能,对图8–10中不同方法在萃取级上的评价指标求平均值,得到平均性能比较结果如表4中所示,表中加粗数值表示最优值.对于稀土萃取流程模拟,数据结果显示SVR与BPNN性能接近,SVR仅仅对水相组分的预测精度略优于BPNN.但两者整体表现较差,不论在水相还是有机相上,两者平均性能都低于其他方法.具有多隐含层结构的5L-DNN学习复杂非线性函数的能力更强,通过隐含层的多层特征提取使得其平均性能优于SVR和BPNN.长短时记忆网络是一种针对长序列数据的深度学习方法,网络基于神经元门控机制可以存取多个时间步长内的特征信息用于下一步预测,本文2L-LSTM的平均R2值高于0.91,相比传统的神经网络预测精度更高.由于技术限制,本文数据集并不是基于等时间间隔采集的,不同样本间的时间间隔可能并不一致,这会影响时序模型的输出效果.图8和图9 也显示2L-LSTM 模型存在输出误差波动较大的现象,针对不同萃取级中组分含量的预测精度不能保持稳定.分析以上方法的性能,在不进行结构创新的情况下,常见的数据驱动模型并未取得很好的效果,输出精度不足以满足流程模拟要求.

表4 平均性能指标比较Table 4 Comparison of average performance indicators
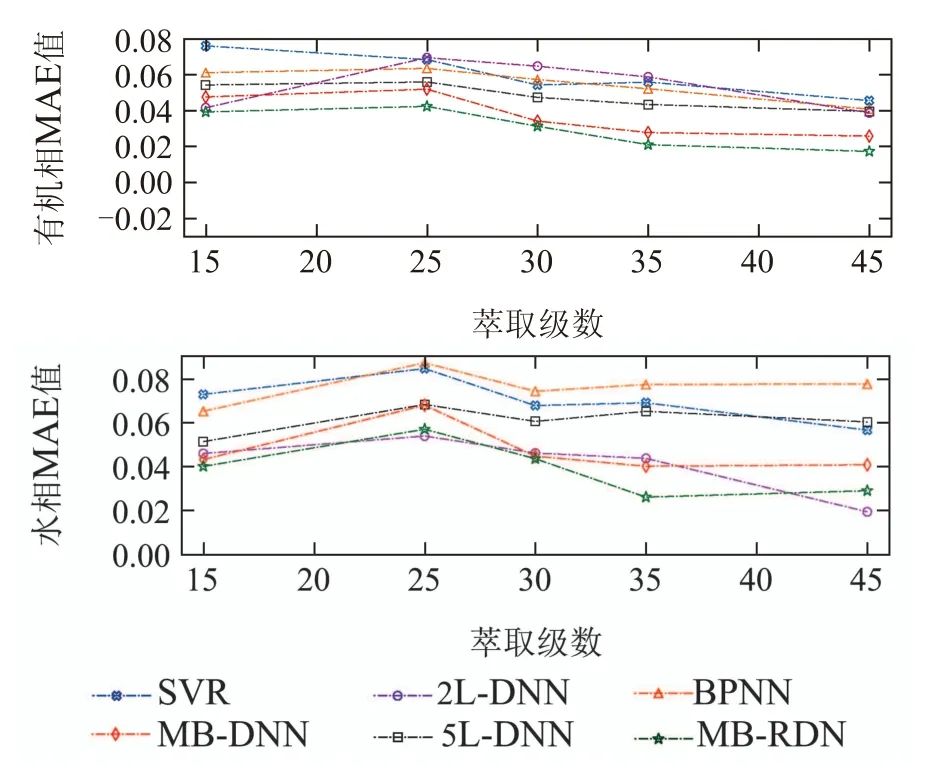
图9 不同方法的RMSE指标对比Fig.9 Comparison for RMSE indicators of different methods
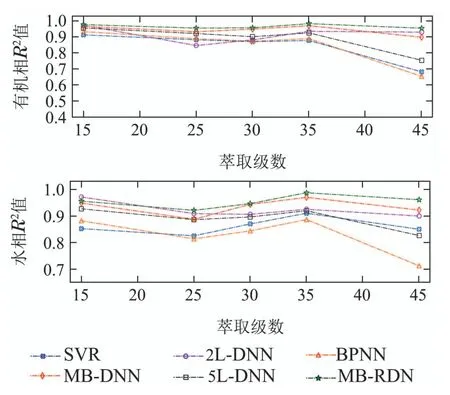
图10 不同方法的R2指标对比Fig.10 Comparison for R2 indicators of different methods
针对存在长流程特性的稀土萃取过程,本文尝试采用具有逐级输出特性的多分支神经网络建立其流程模型.根据表4,具有多分支输出结构的MB-DNN平均性能优于前4种对比方法,证明了多分支网络对于多输出工业过程的有效性.为了缓解梯度消失,结合萃取槽间存在级联耦合的先验信息,在MB-DNN结构基础上进一步提出多分支残差深层网络(MB-RDN)方法.MB-RDN在其分支中引入改进残差结构与特征短接操作实现多层次特征融合,使得分支可以同时提取不同层次的特征用于输出预测.结果显示MB-RDN的输出精度得到明显提升,不论是对有机相还是水相的预测,其平均R2值都能达到0.95以上,在6种方法中表现最优.
萃取流程中位于中段萃取槽的组分含量变化比位于两端的更明显也更频繁,使得单纯通过评价指标不易清晰比较模型预测精度.对此,再绘制三种性能较好的深层模型对中段第30萃取级的组分含量预测输出进行比较,如图11所示.由于5L-DNN未考虑萃取先验信息,只是单向提取信息并在网络最后一层输出目标值,结果显示其预测误差最大,且有部分预测结果超出数据真实范围.本文多分支网络能够以较高的精度贴合实际曲线,特别是基于多层次特征融合的MB-RDN,无论是在有机相还是水相上,其对组分含量变化的预测都有最高精度.

图11 第30萃取级上组分含量预测结果Fig.11 Predicted results for the component content of the 30th extraction stage
为了讨论所提方法的计算负荷以及应用可行性,总结6种模型数据如表5所示.在本文设置下SVR总的训练时间不到300 ms,这是因为SVR遍历所有数据一次即可完成训练.而几个神经网络设定的迭代周期为500,使得相比SVR训练时间更长.根据表5,BPNN在参数量仅为1738的情况下,完成500个迭代周期用时32 s左右.具有深层结构的5L-DNN参数量远大于BPNN,最终训练耗时48.8449 s.MB-DNN是在传统的深层网络基础上引入多分支输出,每个分支末端存在额外的回归层,相比5L-DNN模型参数量增加近2倍.而MB-RDN在分支输出基础上又设计了多层次特征融合机制,导致其参数量进一步增加.尽管2LLSTM仅被设置为双层结构,但由于每个神经元中还包含输入门、遗忘门和输出门操作,使得其训练参数量在6个模型中最多.比较不同模型的训练时间,参数规模最大的2L-LSTM也用时不到66 s,对于离线训练来说,这样的时间消耗是可以接受的.而比较测试时间,6个模型花费的时间差别不大,只有参数规模较大的2L-LSTM 和MB-RDN 超过200 ms.即使是部署于在线预测环境,毫秒级别的预测时间也是实际生产现场可以接受的,能够保证操作人员根据输出结果进行及时的工艺调控.
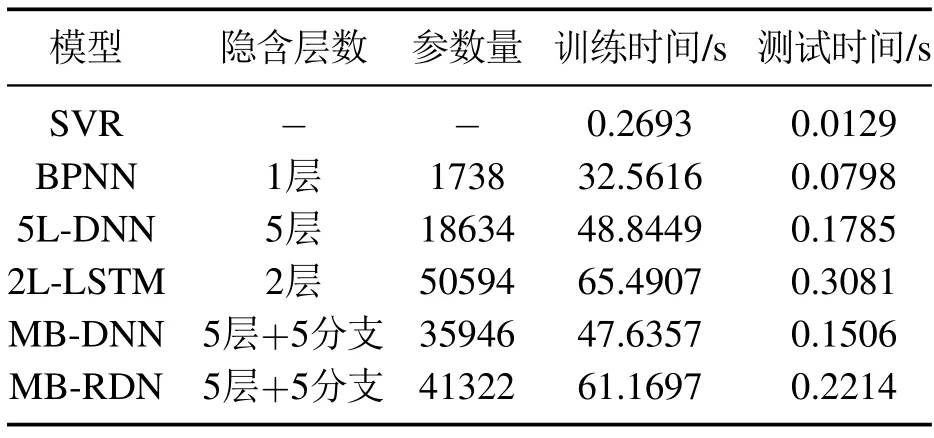
表5 模型的计算负荷对比Table 5 Comparison of calculated loads for the models
生产现场采集的数据不可避免会存在噪声干扰.为此,对训练数据加入噪声干扰后,重新对网络进行训练测试,验证模型的抗干扰性.具体操作如下:对1600例训练数据,随机选择50%(噪声比NR=0.5)的样本加入均值为0,方差为0.1的高斯噪声[30],模拟稀土萃取过程中的环境干扰以及传感器测量偏差.
选择与前述相同的6种方法进行噪声干扰测试,实验设置不变.训练后计算各模型在测试集上输出的平均预测性能指标,结果如表6所示,最优值已加粗显示.在噪声干扰情况下,几种方法的预测性能都存在不同程度的下降.BPNN因为单隐层的结构限制导致抗噪能力不足,其在5个萃取级上的平均R2值已经低于0.7.而SVR在噪声干扰下的性能下降幅度较小,原因是支持向量机只考虑高维特征空间的局部边界线附近的数据点,对异常值不敏感,使得其抗干扰性要优于传统的BP网络.作为深层网络的5L-DNN和2L-LSTM在噪声干扰下会学习到错误的特征分布,两者预测性能也大幅下降.但是同样的实验环境下,两个多分支网络仍然保持着较好的鲁棒性,特别是MBRDN,依然是6种方法中综合性能最好的模型.基于分支结构和多特征融合机制,使得MB-RDN对于错误的特征输入具有一定的抗干扰性.

表6 平均性能指标比较(NR=0.5)Table 6 Comparison of average performance indicators(NR=0.5)
最后,验证本文所提方法对稀土萃取流程的模拟效果.从测试数据中随机选取6例样本,对训练好的MB-RDN模型输入相应样本的工艺参数,得到6例模拟结果如图12(a)–(f)所示.可以看出,所提方法成功模拟了不同萃取槽中组分含量的实际变化情况,且数值误差在可接受范围内.依据MB-RDN所得的模拟结果可以作为后续工艺参数调整的决策依据.
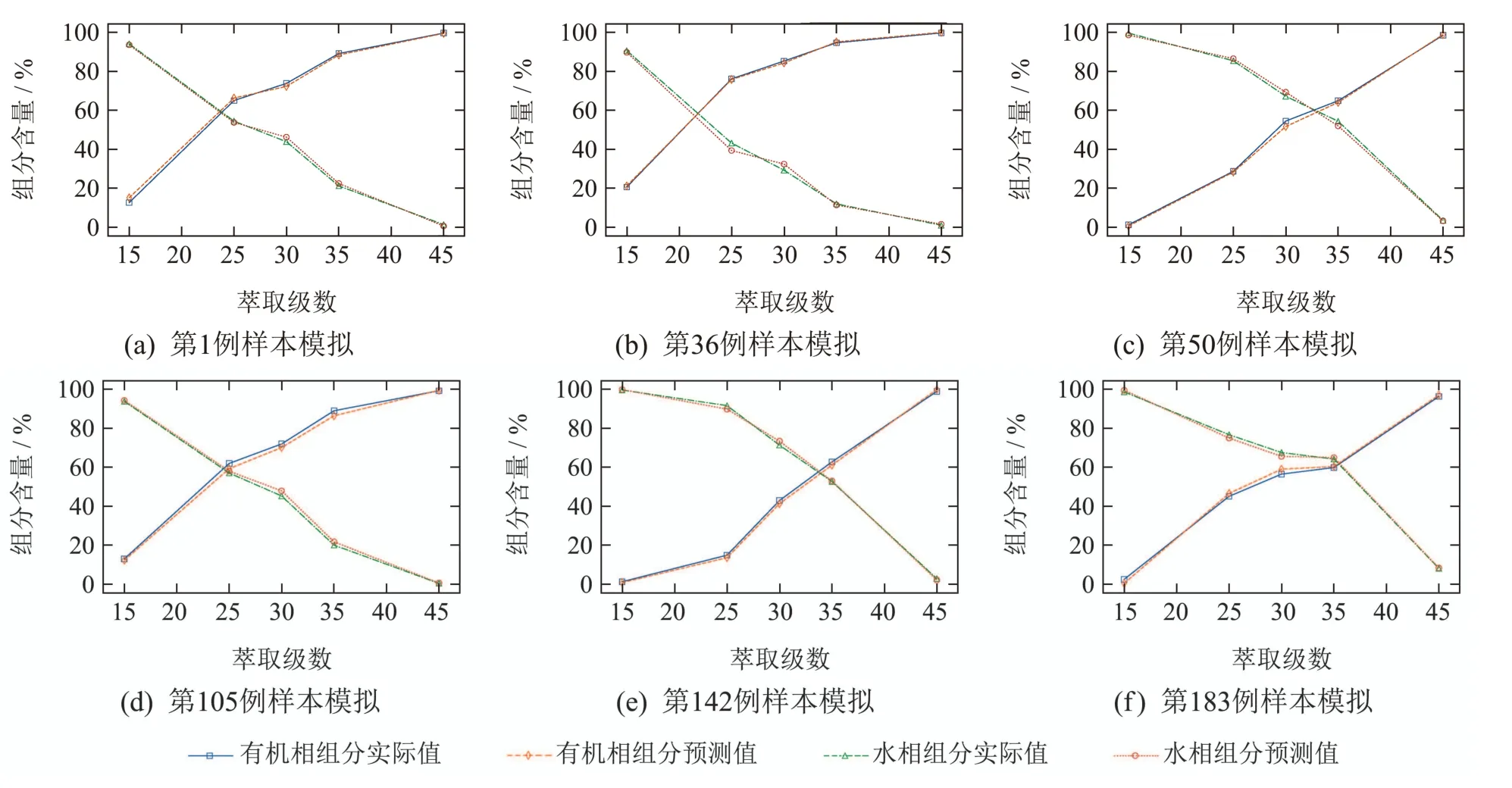
图12 MB-RDN对测试集样本的流程模拟结果Fig.12 Process simulation results of MB-RDN for testset samples
5 结论
针对稀土萃取过程机理复杂,难以准确建立流程模型的问题,本文首次提出采用多分支深层神经网络(MB-DNN)构建萃取流程模型.考虑萃取级间的强耦合特性以及深层网络梯度消失现象,对MB-DNN进行改进,提出一种基于多特征融合机制的多分支残差深层网络(MB-RDN).仿真表明,与SVR,BPNN以及传统深度网络相比,MB-RDN在预测性能上有明显的提升.无论是正常数据还是噪声干扰情况下,通过多层次特征融合充分学习到原始特征、深层特征以及分支耦合特征的MB-RDN在对比方法中都表现出最优性能,能够反映真实的稀土萃取流程.本文所提方法不仅可为稀土萃取过程工艺调整以及智能决策提供支持,也可考虑应用于其他存在强耦合特性的多输出工业过程.
由于本文是近年来首次将多分支神经网络与工业多输出流程建模问题结合的研究,目前只是根据简单的网格搜索确定超参数.进一步还要考虑的是如何根据不同方法确定最优的超参数,以尽可能减少模型计算量.此外,针对工业过程中标签数据采集困难,而本文提出的MB-RDN又无法利用大量易采集的无标签数据,也是下一步需要考虑的方向.

