最值的常见误区引发的包络线问题

华南师范大学附属中学(510630)罗碎海

许多名师是在“教学相长”中成长起来的.学生的求知欲刺激着老师的水平提高,同时学生的错误也使老师反思教学的问题与方法,并有所发现突破.

一、一个传统的错误

二、最小(大)值的定义

最小值的定义对定义在D上的函数y=f(x),若有常数m,对任意x都有f(x)≥m恒成立,并且存在x0∈D,满足f(x0)=m,则m为函数y=f(x)在D上的最小值.

最大值的定义类似.

最小(大)值定义的本质变量恒不小于(或不大于)常量,且等号取到.所以只有在不等式一端为常量的前提下,才可以谈最小(大)值.

原题正确的解法因为x ＞0,所以当且仅当即x=1 时取等号,所以函数的最小值是3.

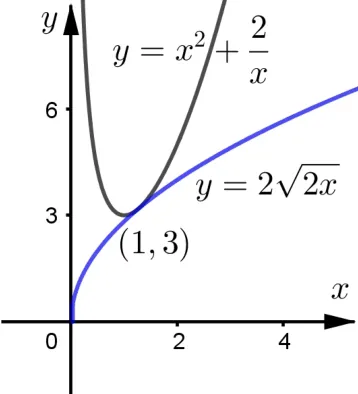
图2

三、反思错误解法中得出的是什么

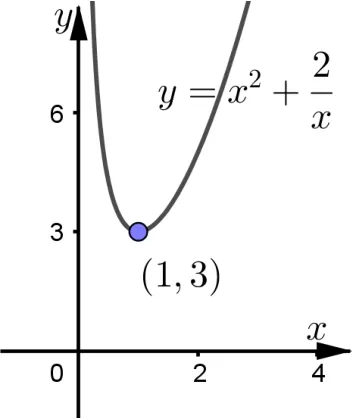
图1

四、代数形式的演变

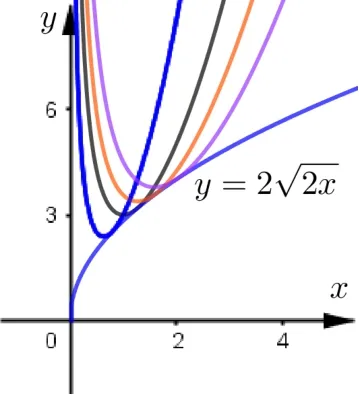
图3

五、包络线的定义及其求法

六、初等方法求包络线问题举例

由以上分析可知求曲线系的包络线的初等方法就是消去参数,具体消参的方法常用的有:应用判别式;应用均值不等式;应用柯西不等式等.我们只能解决一些较简单的问题,许多复杂问题需用高等数学求偏导的方法.

例1求曲线系y-t2=(x-t)2的包络线.

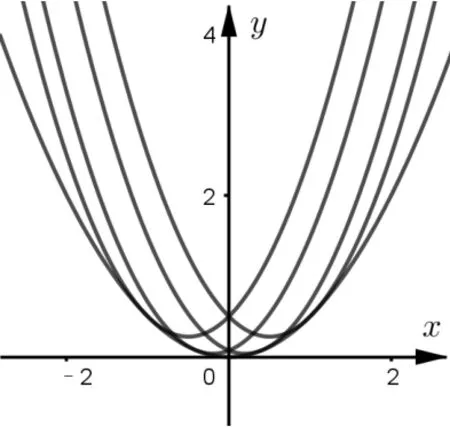
图4

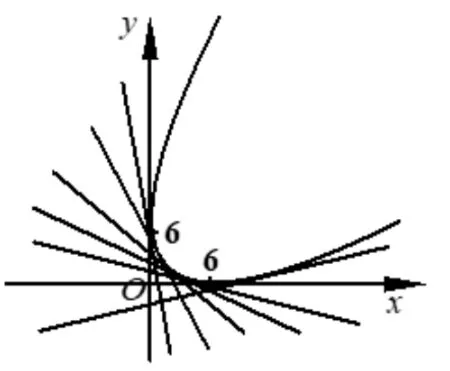
图5

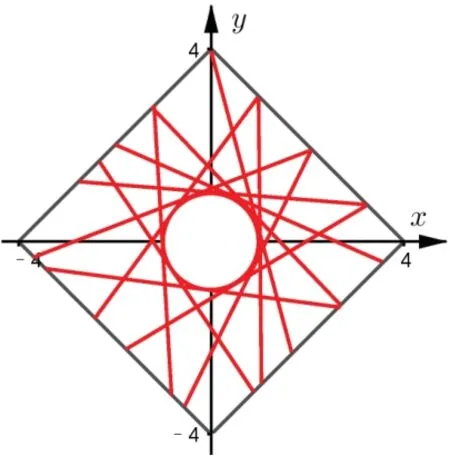
图6

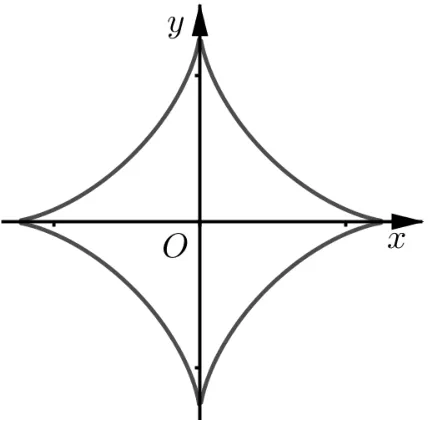
图7

七、圆锥曲线的包络线问题

许多老师在教授椭圆时,用以下问题让学生动手引入新课:

“一张平整的白纸上画有一个半径为R的圆O和圆内一定点A,且OA=a(0＜a ＜R).折叠纸片,使圆周上某一点A′与点A重合.这样的每一种折法留下一条直线折痕MN.当点A′取遍圆周上的所有点时,求所有折痕直线上的点的集合.”

读者不妨取一张白纸画个圆试着折一折,多折几次,不难发现,所有折痕直线好像围成一个椭圆,如图8.下面我们用初等方法证明如下:

性质所有折痕直线围成的图形是以O、A为焦点,长轴的长为R的椭圆,并且这个椭圆和所有折痕直线都相切.

证法1如图8,以O为原点,OA所在的直线为x轴建立直角坐标系,则A(a,0).设折叠时圆O上点A′(x0,y0)与点A重合,则折痕直线MN为线段AA′垂直平分线.

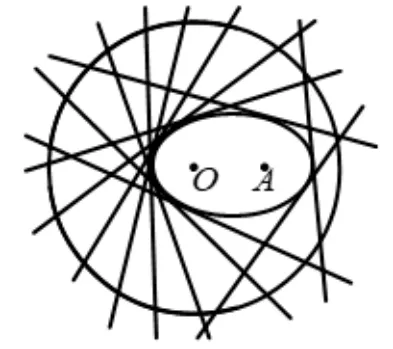
图8

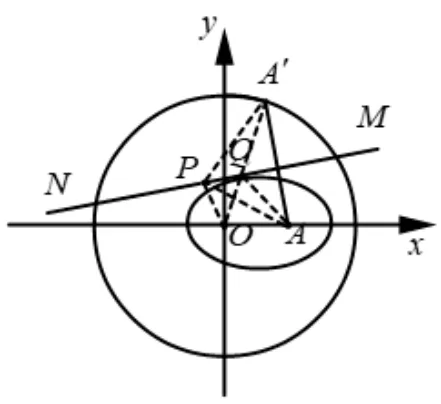
图9

如果把上题中的圆换成直线,则有下面的题目.

变式一张纸上画有直线l和直线外一定有点A,且点A到l的距离为a.折叠纸片,使直线l上某一点A′恰好与点A合.这样的每一种折法都留下一条折痕直线.当点A′取遍直线l上的所有点时,求所有折痕直线上的点的集合.

可以证明:所有折痕直线上的点都在以点A为焦点,直线l为准线的抛物线外部(含边界),且这条抛物线与所有折痕直线都相切.请读者自己证明.

八、高考中的包络问题

多年来,高考数学题中也涉及以包络为背景的问题,当然这些题都可用高中数学知识解决.但若能看透题目的背景,无疑对问题的理解更深刻.试看以下几例:

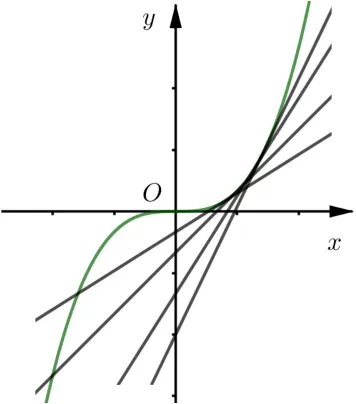
图10

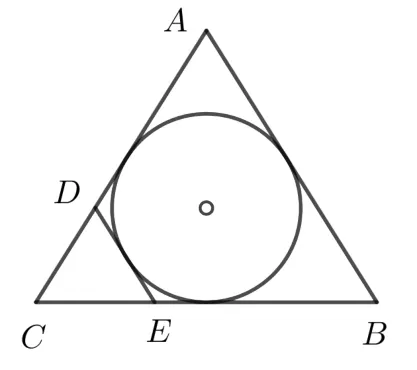
图11

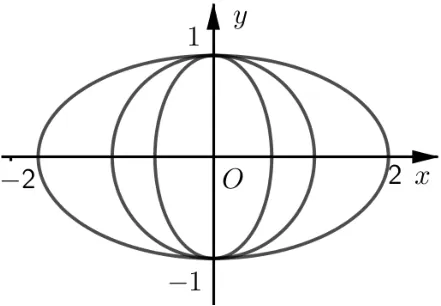
图12

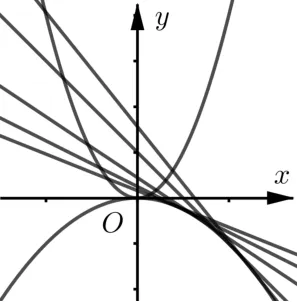
图13

九、构造新的包络线

我们从学生的错误的方法发现一类新的数学问题,并找到解决方法.虽然此法目前不能解决所有问题,而且消参过程需要技巧,许多问题还需继续研究,但它使我们对数学有新的认识与感觉,这正是数学的魅力,是最好的学习,是思维的提升.