正多面体一个定值问题的初等证明

甘肃省静宁县第一中学(743400)刘俊娥

文[1]中,笔者论证了关于正多面体的几个定值问题,在此基础上,文[2]中又论证了正多面体的同心球(球心在正多面体的中心)球面上任意一点P到正多面体各棱的距离的平方和也为定值的问题.但证明过程用的是高等数学的方法.事实上,关于正多面体有关问题的学习,对培养高中生的空间想象能力大有裨益,因此,为了能让高中生更好地理解此定值,本文利用初等方法给出其证明.

命题设正多面体A1A2A3···AV-1AV的棱数为E,棱切球半径为r棱,同心球(球心在正多面体的中心)的半径为R,则同心球球面上任意一点P到正四面体各棱的距离的平方和为定值.

证明首先证明正四面体中成立.如图1所示,正四面体A1A2A3A4的中心为O,棱长为a,点P为正四面体同心球上的任意一点,到各边的距离分别为hi(i=1,2,3,4,5,6),在ΔA1PA2中,有ah1=PA1·PA2sin ∠A1PA2.

图1

由于正六面体、正八面体、正十二面体及正二十面体分别关于其中心对称,易见,欲证成立,只需证明引理在正六面体中成立即可.

如图2,设正方体的棱长为2a,建立如图所示的空间直角坐标系,则A1(a,-a,a),A3(-a,a,a),A5(a,a,-a),A7(-a,-a,-a),点P为正四面体A1A3A5A7同心球上的任意一点,P(x,y,z),设同心球半径为R,若与所成的角分别为θi(i=1,3,5,7),则有,

图2

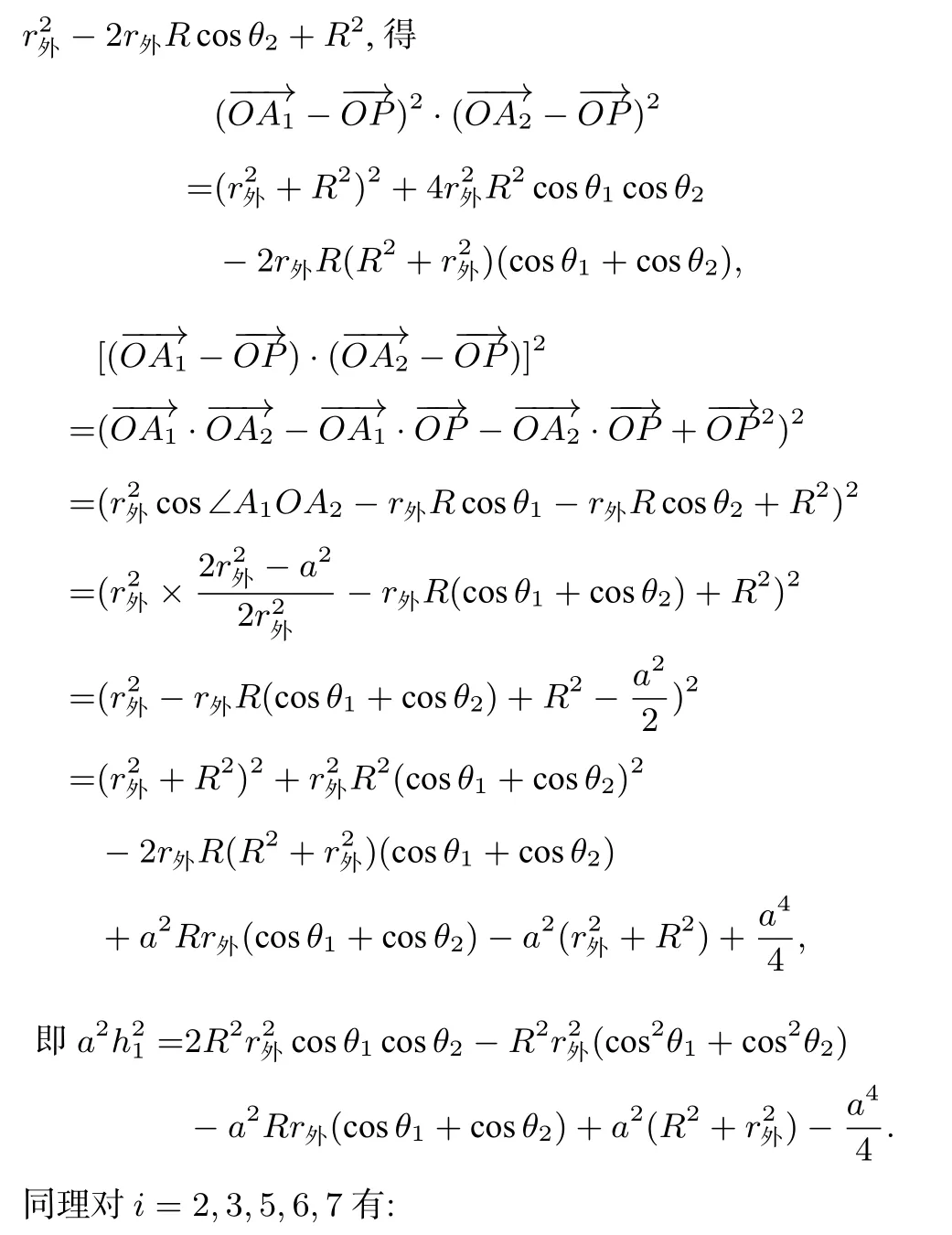
故命题在正六面体中成立.

下面证明命题在正八面体中成立.

如图3,在正八面体中,设外接球半径为r外,棱长为a,1,2,3,4,5,6)所成的角分别为θ1,θ2,···,θ6,且满足cosθi=-cosθ7-i(i=1,2,3).

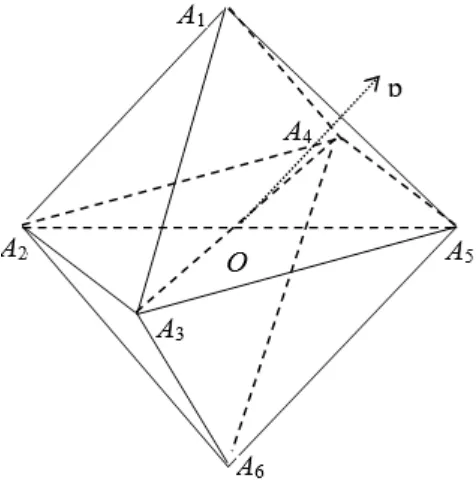
图3

设点P到棱A1Ai+1的距离为hi(i= 1,2,3,4),到棱A6A6-i(i= 1,2,3,4)的距离为hi+7(i= 1,2,3,4),到棱AiAi+1(i= 2,4)的距离分别为hi+8(i= 2,4),到棱AiAi+2(i=2)的距离为hi+8(i=2),到棱AiAi+2(i=3)的距离为hi+9(i=3).则有

根据正十二面体和正二十面体的对称特点,总有一对顶点的连线过其中心O,按上述证明亦可以证明命题在正十二面体和正二十面体中成立(本文从略).

图4

图5