塑料经纱管振程工作台驱动机构定位精度分析

王延蒙，纪 红

(济宁职业技术学院，山东 济宁 272073)

0 引言

经纱管在纱线加捻卷绕过程高速旋转，所引起的振动是影响纱线质量的重要因素[1-3]。目前，一般采用离线式抽样检测，依赖人工安装锭子和经纱管，效率极低。而采用由弧面分度凸轮机构驱动的经纱管振程自动化检测机构中，弧面分度凸轮机构的定位精度是影响纱管振程检测结果的重要因素。目前，针对弧面分度凸轮定位精度的研究主要有：常宗瑜[4]等考虑到弧面分度凸轮间隙的影响，对弧面分度凸轮动力学问题进行实验研究，给出了不同转速条件下工作转盘的加速度响应，结果表明工作盘处的动力学响应与输出轴的动力学响应有着较大的不同。刘海[5]等从实验的角度对弧面分度凸轮进行动分度精度检测和静分度精度的检测。王晓飞[6]等以三坐标测量机进行弧面分度凸轮测量评定凸轮的几何误差，其主要是针对静态测量，主要研究对象包括廓面偏差、螺旋线偏差以及轴向界面偏差，建立了误差评定标准。王海燕[7]等建立了弧面分度凸轮轮廓误差评定模型，通过样条差值来应用于实际的检测。KUANG[8]等从主动轮的转速入手，分析了速度对输出轴工作盘残余振动的影响关系。

针对弧面分度凸轮机构定位精度对纱管振程检测的影响，笔者通过分析纱管振程检测对多工位转盘定位精度的工艺要求，对弧面分度凸轮进行动力学仿真，确定弧面分度凸轮机构能够在纱管振程检测过程中将定位精度保证在合理范围之内。

1 经纱管振程检测工艺要求

经纱管振程自动化检测平台将插管、增速检测、锭子刹车、拔管等工艺分布在4个工位上，见图1。

1—插管；2—增速检测；3—刹车；4—拔管。

纱管振程检测在锭子增速工位进行。设工作台直径d1为600 mm，纱管分布圆直径d2为500 mm，纱管检测处直径d3为18 mm，假设弧面分度凸轮机构在定位过程中出现θ的偏差，对经纱管振程测量产生的偏差计为△x，如图2所示，则△x与纱管振程x应满足△x/x≤ε。其中，ε表示纱管振程检测的误差。

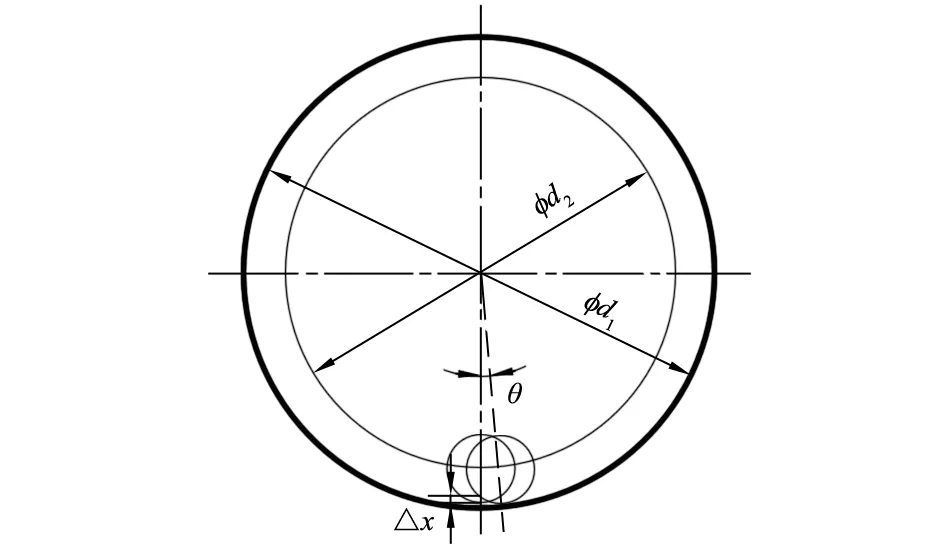
图2 经纱管振程测量产生的偏差局部示意

由于纱管直径相对于均布圆直径较小，且偏移角度θ很小，因此可近似认为纱管偏移沿水平方向进行，偏差△x主要是由于水平移位导致测量点的偏移，如图3所示。则△x可表达为：

1—经纱管；2—移位经纱管。

△x=r3―[r32―(r2θ)2]1/2

图4给出了经纱管振程与工作台定位角度的关系。经纱管振程检测的误差ε要求控制为5%以内，不同类型经纱管振程的幅值范围并不相同。如：管长为180 mm的G型经纱管对于振幅要求小于0.15 mm，其弧面分度凸轮机构在定位过程中出现的偏差应小于0.086°；管长为230 mm的G型经纱管对于振程幅值要求小于0.35 mm，其弧面分度凸轮机构在定位过程中出现的偏差应小于0.110°。由于多工位转盘要满足各种类型纱管的检测，因此以经纱管振程最小的0.15 mm为准，验证弧面分度凸轮机构的定位精度。

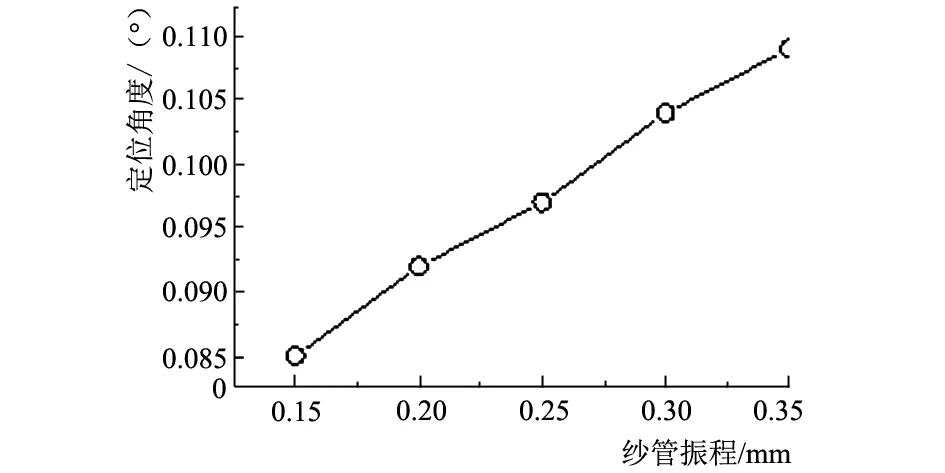
图4 经纱管振程与工作台定位角度关系

2 弧面分度凸轮机构动力学仿真

由纱管振程检测工艺要求可知，在驱动过程中定位精度及平稳性是影响检测结果的关键因素，因此仿真过程重点观测转盘位移、速度和加速度的动力学变化情况。经纱管振程检测驱动机构设计参数如表1所示，利用Pro/E建立弧面分度凸轮模型，并导入ADAMS动力学进行仿真分析，仿真模拟设计如表2所示。通过虚拟模型分析位移、速度和加速度在传动过程中的变化，以保证弧面分度凸轮能够精准的实现多工位驱动。

表1 经纱管振程检测驱动机构设计参数

表2 仿真模拟设计

3 仿真验证

在ADMAS仿真中将步长设计为400，即曲线图包括400个数据点，导出的数据点曲线如图5所示。

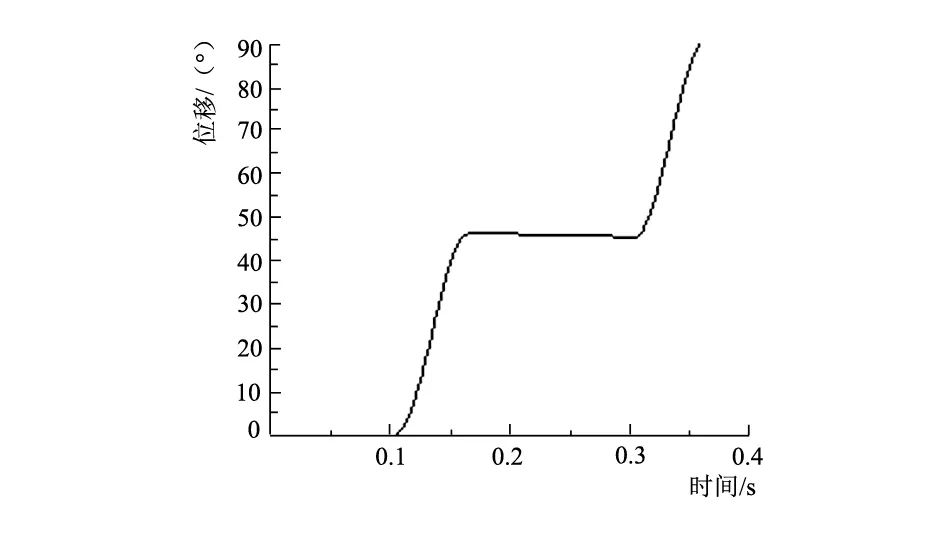
a) 工作盘角位移变化曲线

3.1 工作盘角位移变化曲线

工作台在转位期角位移偏差为0.002 3°。在弧面分度凸轮机构由转位至定位的瞬间位移偏量较大，误差率达到5.98%，在0.015 s后趋于理想位置，经纱管振程检测工艺时间之内最大误差为2.51%，最小误差仅为0.87%。

3.2 工作台角速度的变化

由角速度变化曲线可知，在工艺时间内，弧面分度凸轮定位准确，基本无大范围的抖动，满足在该时间内对纱管振程检测的位置要求。

3.3 工作台角加速度的变化

在定位时间内，角加速度存在一定的波动。仿真结果与理论值差异，主要是因滚子与主动轮之间的间隙及建模误差所引起。

4 结语

4.1为了验证经纱管振程工作台驱动机构的定位精度，根据经纱管振程检测的工艺要求，通过对不同类型的合格经纱管的振程所要求的测量精度进行分析，得出满足检测各种经纱管所需要的工作台驱动定位精度。

4.2利用Pro/E和ADAMS对弧面分度凸轮进行动力学仿真，仿真结果表明在经纱管振程检测工艺时间内的最大误差为2.51%、最小误差仅为0.87%，弧面分度凸轮的角速度和角加速度曲线基本平稳，说明弧面分度凸轮机构具有良好的定位性能，能够满足经纱管振程多工位驱动的要求。