圆的数学性质在动力学问题中的应用

■四川省资中县教育研究室 邓贤彬

圆是生活中常见的几何图形,也是平面几何中研究较多的数学模型。熟练掌握圆的几何性质、圆与直线的位置关系并巧妙结合物理情景解决物理问题,不仅可以拓宽解题思路,而且能够提高解题速度和提升解题能力。下面利用圆的特点并结合物理规律迅速、准确地求解力的动态平衡、匀变速运动等动力学问题,权作抛砖引玉之说,愿对读者有所帮助和启迪。

一、利用同圆或等圆解决力的动态平衡问题

1.圆的数学性质:在同圆或等圆中,同弧(等弧)所对的圆周角相等,相等的圆周角所对的弧长也相等。如图1所示,∠ACB=∠ADB=∠AEB。

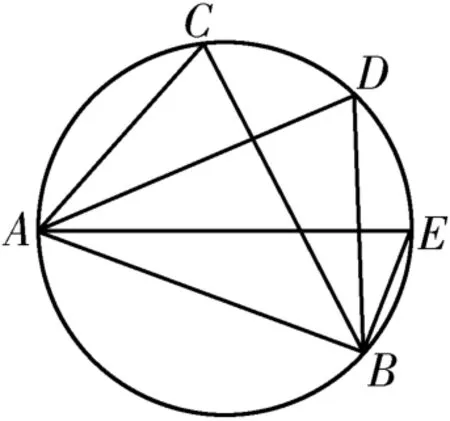
图1

2.物理模型:在三个力的动态平衡问题中,若某个力的大小和方向保持不变,另两个变化力的夹角始终保持不变,则通过定量计算得出正确答案的难度相当大,而利用圆的有关性质通过作动态变化图往往可以迅速、直观地得出正确答案。

例1如图2所示,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住轻绳的另一端N。初始时,OM段竖直且MN段被拉直,OM段与MN段之间的夹角为现将重物向右上方缓慢拉起,并保持夹角α不变,在OM段由竖直被拉到水平的过程中( )。

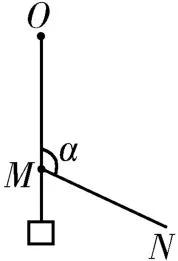
图2

A.MN段中的张力逐渐增大

B.MN段中的张力先增大后减小

C.OM段中的张力逐渐增大

D.OM段中的张力先增大后减小

解析:题目中的重要信息包括三个,一是重物在缓慢运动中始终只受三个力的作用,如图3甲所示;二是根据受力平衡,将三个力平移,则这三个力必然构成首尾相接的三角形,如图3乙所示;三是这三个力中的mg的大小、方向始终保持不变,另外两个力TMN和TOM的夹角α始终不变。

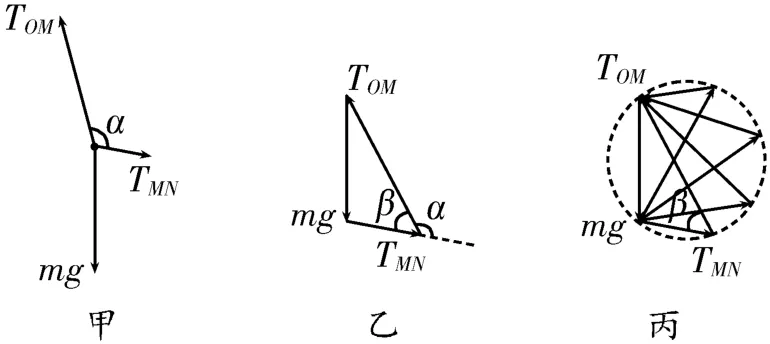
图3

因为mg保持不变,且夹角α保持不变,即图3乙中的β角也保持不变,所以在封闭的力的矢量三角形中,表示mg的边长不变,其所对的角β也保持不变。根据圆的性质,过三角形的三个顶点作一圆,如图3丙所示,改变拉力TMN和TOM的方向,其交点始终在圆周上。根据动态图可知,在OM段由竖直被拉到水平的过程中,TMN由零逐渐增大,当OM段水平时TMN(直径所对的圆周角为直角)最大,TOM先增大后减小。

答案:AD

方法与技巧:(1)力的平衡是历年高考必考的知识点之一,同学们在复习备考时必须重视知识的落实,强化解题技能的训练,提高解题的速度和准确度。(2)当物体受到三个力作用处于平衡状态,其中一个力恒定,另一个力的大小变化而方向不变,第三个力的方向变化而大小不变(或者另外两个力的大小和方向均变化但其夹角保持不变)时,应用作圆的动态图的方法解决则较为直观、快捷。

实战演练1:(2021年高考湖南省等级性考试)质量为M的凹槽静止在水平地面上,内壁为半圆柱面,截面如图4所示,A为半圆的最低点,B为半圆水平直径的端点。凹槽恰好与竖直墙面接触,内有一质量为m的小滑块,用推力F推动小滑块由A点向B点缓慢移动,力F的方向始终沿圆弧的切线方向,在此过程中所有摩擦均可忽略。下列说法中正确的是( )。

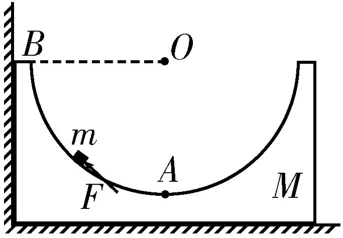
图4

A.推力F先增大后减小

B.凹槽对滑块的支持力先减小后增大

C.墙面对凹槽的压力先增大后减小

D.水平地面对凹槽的支持力先减小后增大

答案:C 提示:对滑块进行受力分析,如图5甲所示,滑块处于动态平衡的变化过程中(图中的θ由0增大到90°的过程中),重力mg保持不变,且F与N的夹角一直为90°,因为三个力的合力始终为零,所以可以以重力大小mg为直径作一个圆,则F和N恰好是夹角始终为90°的两条弦,如图5乙所示。观察图像可以直接得出在θ从0 增大到90°的过程中,F逐渐增大,N逐渐变小,选项A、B错误。在θ从0增大到90°的过程中,F的竖直分力一直增大,而水平分力先增大后减小。对由滑块和凹槽组成的整体进行受力分析,如图5丙所示,根据平衡条件,结合F的竖直分力和水平分力的变化规律可知,N2一直减小,N1先增大后减小,选项C正确,D错误。

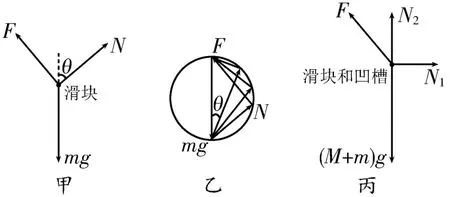
图5

二、利用“等时圆”比较物体的运动时间

1.圆的数学性质:半圆(直径)所对的圆周角是直角,90°的圆周角所对的弦是直径。

2.“等时圆”的物理结论:

(1)定性结论:质点从竖直圆环上沿不同的光滑弦上端由静止开始下滑到圆环的最低点所用的时间相等(如图6甲所示),或者质点从竖直圆环的最高点沿不同的光滑弦由静止开始滑到下端所用的时间相等(如图6乙所示)。

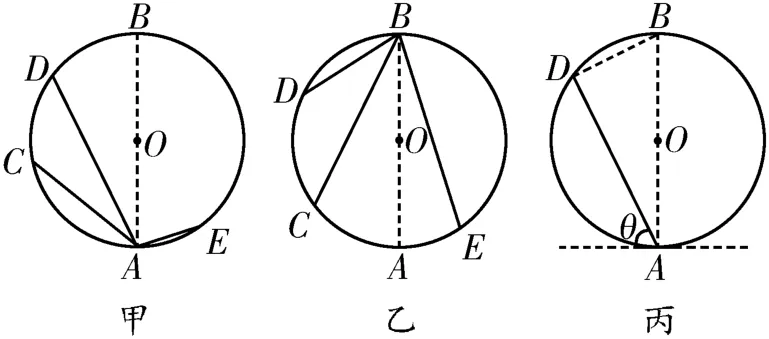
图6

证明:以图6甲中的DA弦为例,设DA弦与水平面之间的夹角为θ,如图6丙所示,物体沿DA弦做初速度为零的匀加速直线运动,根据牛顿第二定律得mgsinθ=ma,根据运动学公式得xDA=,连接BD,则∠ADB=90°(直径所对的圆周角等于90°),根据几何关系得∠DBA=θ,xDA=2Rsinθ,解得,即时间t与角度θ无关,只由圆的半径R和当地的重力加速度决定。

3.解题思路:

(1)分析模型条件:①多条相交于同一点的光滑倾斜直轨道为同一圆的不同弦;②质点由静止开始从轨道一端滑到另一端。

(2)确定运动起点(或者运动终点):起点为圆周的最高点,或者终点为圆周的最低点。

(3)作等时圆:①过最高点作竖直线;②以某轨道为弦作圆心在竖直线上的圆。

(4)定性比较时间:①轨道端点在圆周上,质点运动时间相等(等时圆);②轨道端点在圆周内,质点运动时间短些;③轨道端点在圆周外,质点运动时间长些。

(5)定量分析时间:根据牛顿第二定律得mgsinθ=ma(θ为弦与水平面之间的夹角),解得a=gsinθ,根据运动学公式得x=,利用数学知识找出x与圆周的半径R、弦与水平面之间的夹角θ的关系,联立所列关系式便可写出关于时间t的定量表达式。

例2如图7所示,OA、OB和AD是竖直平面内三根固定的光滑细杆,O、A、B、C、D位于同一圆周上,C为圆周的最高点,A为圆周的最低点,O＇为圆心。每根细杆上都套着一小滑环(图中未画出),将两个滑环从O点无初速度地释放,将一个滑环从D点无初速度地释放,用t1、t2、t3分别表示滑环沿OA、OB、DA杆下滑到A、B两点所用的时间,则下列关系式中正确的是( )。

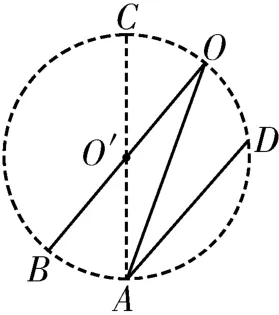
图7

A.t1=t2B.t2＞t3

C.t1＜t2D.t1=t3

解析:沿OA杆和DA杆运动的两个滑环,A为圆周的最低点,根据“等时圆”结论得t1=t3,选项D 正确。沿OA杆和OB杆运动的两个滑环,因为O不是圆周的最高点,所以“等时圆”结论不成立,只能定量分析。假设还有一根光滑固定细杆CA,因为xCA=xOB,aCA＞aOB,所以tCA＜tOB=t2。再由“等时圆”结论得tCA=t1=t3,因此t1＜t2,t2＞t3,选项A 错误,B、C正确。

答案:BCD

例3如图8所示,在倾角为θ的斜面上方的A点放置一光滑的木板AB,B端刚好在斜面上。木板与竖直方向AC所成夹角为α,一小物块自A端沿木板由静止下滑,要使物块滑到斜面上所用的时间最短,则α与θ角的大小关系应为 ( )。

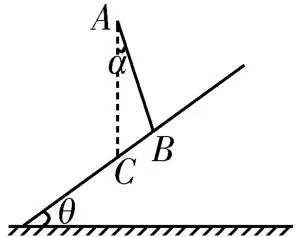
图8

A.α=θB.α=

C.α=D.α=2θ

解析:物块在竖直平面内沿光滑的木板由静止开始下滑,满足“等时圆”模型中质点运动的特点,因此可以以A点为圆的最高点,使得圆心在AC连线上,以AB为弦作一个圆。根据“等时圆”的定量关系可知,要使物块滑到斜面上所用的时间最短,即要求作出的圆半径最小,又有B点在斜面上,则这个圆应该与斜面相切,即B为圆与斜面的切点,如图9所示。因为B为圆与斜面的切点,则OB⊥BC,根据数学知识得∠COB=θ=2α,即

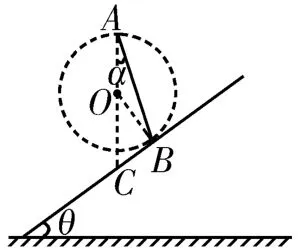
图9

答案:B

例4如图10所示,圆弧AB是半径为R的圆弧,在圆弧AB上放置一光滑木板BD,一质量为m的小物体从木板BD的D端由静止下滑,然后冲向水平面BC,在水平面BC上滑行距离L后停下。不计小物体滑至B点时的能量损失,已知小物体与水平面BC之间的动摩擦因数为μ。求小物体在木板BD上下滑的过程中,重力做功的平均功率。

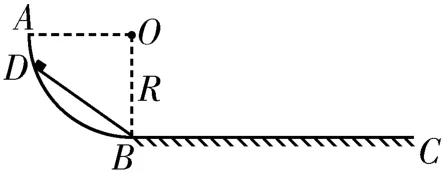
图10

解析:根据动能定理可知,小物体从D点运动到C点的过程中有W重-μmgL=0,解得W重=μmgL。根据“等时圆”结论可知,小物体从D点运动到B点所用的时间等于小物体从圆周的最高点下落到B点所用的时间,即因此小物体在木板BD上下滑的过程中,重力做功的平均功率

方法与技巧:(1)定性比较竖直圆面内的不同光滑斜面上物体运动的时间长短问题,构造“等时圆”是一种快捷的解题方法,尤其是在遇到需要比较多个物体的运动时间时,相当简捷。(2)沿不同光滑弦运动的物体所用的时间(R为圆的半径)为一定值,也等于做自由落体运动的物体下落高度2R所用的时间,此结论也可用于定量计算。

实战演练2:(2021年高考全国甲卷) 如图11所示,将光滑长平板的下端置于铁架台水平底座上的挡板P处,上部架在横杆上。横杆的位置可在竖直杆上调节,使得平板与底座之间的夹角θ可变。将小物块从平板与竖直杆交点Q处由静止释放,物块沿平板从Q点滑至P点所用的时间t与夹角θ的大小有关。若θ由30°逐渐增大至60°,则物块的下滑时间t将( )。

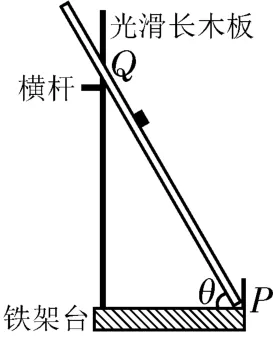
图11

A.逐渐增大

B.逐渐减小

C.先增大后减小

D.先减小后增大

答案:D 提示:如图12所示,先过P点作一条竖直线PA,再作与水平面之间的夹角为30°的直线PQ1,然后作线段PQ1的中垂线与竖直线PA相交于O1点,以O1为圆心、O1P为半径作圆(圆1),圆1与竖直杆的交点为Q1、Q2,根据“等时圆”结论可知,物块从Q2、Q1两点分别下滑至P点所用的时间相等,即tQ2P=tQ1P。在竖直线PA上找一点O2(O2到竖直杆的距离d=O2P),以O2为圆心、O2P为半径作圆(圆2),使圆2 与竖直杆相切于Q3点。因为圆2的直径小于圆1 的直径,所以tQ3P＜tQ2P=tQ1P,且弦PQ3与水平面之间的夹角为45°。因为θ角由30°逐渐增大至60°,所以物块的下滑时间先减小后增大。

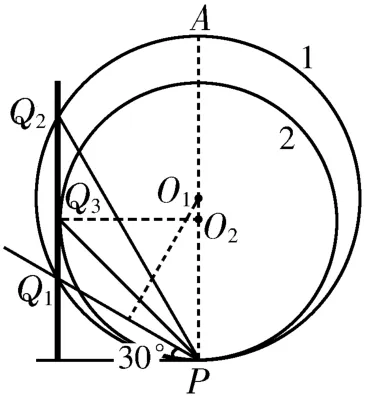
图12