三道相似习题多解的比较

■重庆市江津第二中学校 黄 泌

直线运动涉及的公式繁多,同学们在求解直线运动问题时对公式的选择比较困难,利用相似习题的一题多解,通过相似习题多种解法的比较,有助于同学们熟练掌握并灵活选用这些公式。下面以三道相似习题的部分解法为例进行讨论。

一、相似习题多种解法展示

例1一物体做匀速直线运动,它在两段连续相等时间内通过的位移分别是24 m和64 m,连续相等时间为4 s,求该物体的初速度、末速度和加速度大小。

解法一:如图1所示,设物体到达A点时的速度为vA,到达B点时的速度为vB,到达C点时的速度为vC,加速度为a,根据位移公式得,根据速度公式得vB=vA+at,vC=vA+a·2t,其中sAB=24 m,sBC=64 m,t=4 s,解得vA=1 m/s,a=2.5 m/s2,vC=21 m/s。

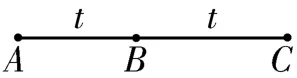
图1

解法二:根据相邻相等时间位移差公式得Δs=at2,解得a=2.5 m/s2。根据位移和速度公式得sAB=vAt+,vC=vA+a·2t,解得vA=1 m/s,vC=21 m/s。

解法三:根据平均速度等于中间时刻瞬时速度得v1==6 m/s,v2==16 m/s。两中间时刻之间的时间差Δt=4 s,则

例2一质点做匀变速直线运动,依次通过A、B、C、D四点,已知经过AB段、BC段和CD段所用的时间分别为t、2t、3t。AC段和BD段的长度分别为x1和x2,则质点经过C点时的瞬时速度为( )。

解法一:如图2所示,设质点到达A点时的速度为v0,到达B点时的速度为vB,加速度为a,根据位移公式得x1=v0·3t+,解得设质点到达C点时的速度为vC,根据速度公式得vC=v0+a·3t,解得vC=

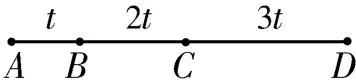
图2

解法二:如图3所示,利用平均速度等于中间时刻瞬时速度可得,质点通过AC段的平均速度是中间时刻t1=1.5t的瞬时速度,即;质点通过BD段的平均速度是中间时刻t2=3.5t的瞬时速度,即v2=两中间时刻之间的时间差Δt=t2-t1=2t,则设质点到达C点时的速度为vC,以v1为起点,根据速度公式得vC=v1+a·1.5t,解得vC=

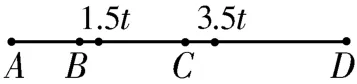
图3

答案:B

例3如图4所示,一物体从O点由静止开始做匀加速直线运动,途经A、B、C三点,其中AB段的长度为2 m,BC段的长度为3 m。若物体通过AB段和BC段所用的时间相等,则O、A两点之间的距离等于( )。

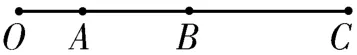
图4

解法一:设物体到达A点时的速度为vA,物体通过AB段和BC段所用的时间为t,加速度为a,根据位移公式得sAB=vAt+两式相减得Δs=sBC-sAB=at2=1 m,解得设物体通过OA段所用的时间为t1,则O、A两点之间的距离

解法二:根据相邻相等时间内的位移差公式得Δs=sBC-sAB=at2=1 m,根据位移公式得,解得设物体通过OA段所用的时间为t1,则O、A两点之间的距离

解法三:利用平均速度等于中间时刻瞬时速度可得,物体通过AB段中间时刻的瞬时速度物体通过BC段中间时刻的瞬时速度加速度,根据位移公式得sAB=vAt+,解得设物体通过OA段所用的时间为t1,则O、A两点之间的距离

答案:A

二、解后反思

1.题意上的比较:审题是解决物理试题的最初环节,通过审题可以明确命题者的意图,厘清题目中各个物理量之间的关系,形成解决问题的思路。上述三个习题均是匀变速直线运动问题,题干都给出了各段的位移和时间。其中例1、例3两题干中有相邻相等时间间隔的条件,例2题干中却不是相邻位移,时间也不相等,因此解法有所不同。例2 不能直接从Δs=at2的角度进行思考;例1 给出的条件较多,因此可供选择的解法也较多;例3给出的条件较少,且关系相对隐蔽,求解要困难一些。

2.解题方法上的比较:

(1)在三道习题的题干中都给出了时间、位移关系,均能从匀变速直线运动的位移、速度等基本公式入手进行求解,只是在运算上相对复杂一些。

(2)三道习题都能利用平均速度等于中间时刻瞬时速度这一结论进行求解。需要注意的是在例2中两瞬时速度的时间关系容易出错,正确作出示意图有利于厘清时间关系。

(3)例1、例3从解题思路上讲完全一致,但从试题难度上讲例3 的难度相对大一些,原因是题干中给出的物理量较少,在解题的过程中需要将at2或vAt看作整体代入运算,这就要求答题者要有一定的观察力,能够在运算过程中想到后面可能用到的关系式。

总之,习题的作用是促进答题者对知识的理解和领悟,匀变速直线运动涉及的公式和推论繁多,通过一题多解的训练同学们能够尽快熟悉这些公式,通过对同类试题多种解法的比较同学们能够掌握各个公式的特点并灵活运用。