车体支撑刚度对车体垂向弯曲的影响分析
张远亮,张立民
(1 四川城市职业学院 智能制造与交通学院,成都610110;2 西南交通大学 牵引动力国家重点实验室,成都610031)
随着我国动车组速度的不断提高,对整个动车组系统的安全性要求越来越高,用于描述车辆振动特性的模态参数也越来越得到人们的重视。车体的模态是车体本身固有的振动特征,同时整备车体的1 阶垂向弯曲频率是考核动车刚度的重要指标参数[1-3]。我国在铁道标准中TB/T 3115—2005《机车车辆动力学性能台架试验方法》中明确规定:在整备条件下,车体1 阶垂向弯曲振动频率和转向架的沉浮运动频率、点头运动频率之比大于1.4 倍;在没有检测沉浮运动频率、点头运动频率的情况下,整备车体的1 阶垂向弯曲频率应当大于10 Hz[4-6]。
车体模态参数的识别主要包括仿真计算以及现场试验等方法。在仿真计算时一般利用有限元软件将车体简化为壳单元计算模态,计算时一般为自由模态,即无约束模态;现场测试试验时,车体一般坐落于转向架上,测试结果为约束模态。在测试模态时,目前的相关标准并未严格要求支撑情况,一般为弹性橡胶垫支撑(针对白车体)以及正常的坐落于转向架上即可(针对整备车)。因此支撑刚度对车体模态的影响非常有必要深入研究。
1 车体简化模型理论
由于车体长度大于宽度和高度的5 倍,故可以将车体简化为欧拉梁。车体弹性模态不考虑转动惯量及剪切变形的影响[4]。由于阻尼不影响车体系统的特征频率和特征向量,故系统简化为无阻尼系统。 车体与支撑系统振动简化[4]如图1所示。

图1 车体与支撑系统振动简化图
虚线为车体结构的初始位置,实线为车体结构的振动位置。
将车体结构等效为自由振动的梁,其第n阶振型的广义坐标运动方程[4]为式(1):
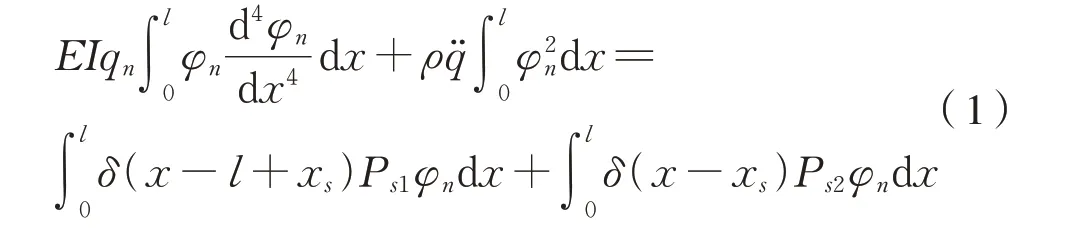
式中:EI为车体结构的垂向抗弯刚度;ρ为车体结构 的 线 密 度,ρ=mc/l;Ps1为1 位 端 二 系 悬 挂 垂 向作用力;Ps2为2位端二系悬挂垂向作用力。
其中:

φn是车体结构的弯曲振型函数[4],为式(2):

整理得式(3):

系统的刚体运动方程为式(5)、式(6):

且
由模态叠加原理[2]可知:
对于列车车体,取其1 阶垂弯振型能得到垂向弯曲变形较好的近似[1]。联立式(4)~式(9),得到车体刚柔耦合振动方程式(10):

式中:z为广义位移量,{z}=[zc,θc,q1]T
M为广义质量矩阵为式(11):

K为广义刚度矩阵为式(12):

式中:
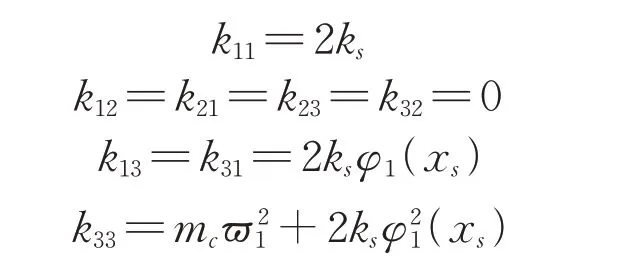
求解矩阵方程(10),即可得到车体的固有弯曲频率及振型。在每个固有频率中,总有一个自由度的运动是主要运动形式,即振幅相对最大。
故在某一频率f下,车体1 阶垂向弯曲振幅相对最大时,该频率即为车体1 阶垂向弯曲频率。
2 数值计算


图2 支撑刚度ks与1 阶垂向弯曲频率f 关系(数值计算结果)
由图2 可以得出:随着支撑刚度ks的增大,1 阶垂向弯曲频率f逐步增大,但增加十分有限,当刚度增加10 倍时,垂弯频率仅仅增加0.6 Hz 左右。
3 有限元仿真
将车体地板、侧墙等简化为壳单元,因只考虑支撑刚度对车体垂向弯曲频率的影响趋势,故车下吊挂设备均不予考虑。
考虑车体为空气弹簧支撑时,将每个空气弹簧简化成16 根弹簧组合。只考虑每根弹簧的垂向刚度,用Spring-Damper14 单元模拟弹簧[7-12]。
空簧刚度变化范围为2×104~1×106N/m,进行有限元仿真,计算结果见表1:

表1 有限元仿真结果
支撑刚度ks与1 阶垂向弯曲频f关系(有限元仿真结果)如图3 所示,由图3 可以得出:随着支撑刚度ks的增大,1 阶垂向弯曲频率呈缓慢增加趋势,但增加幅度非常小,当刚度增加10 倍时,垂弯频率仅仅增加0.2 Hz 左右。支撑刚度的增加与自由模态及无约束模态相差甚微。
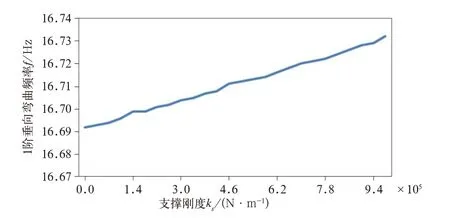
图3 支撑刚度ks与1阶垂向弯曲频率f关系(有限元仿真结果)
4 试验验证
对某高速动车组整备状态,空气弹簧完全充气和完全失气状态下进行多点正弦扫频激励,测试车体1 阶垂向弯曲频率。车体坐落于转向架上,车体分为9 个截面,每个截面4 个测点,测试垂向和横向加速度。空气弹簧结构如图4 所示。

图4 空气弹簧结构
空气弹簧采用橡胶堆弹性支撑,橡胶堆与空气弹簧串联,在空气弹簧完全失气状态下,橡胶堆仍然起弹性支撑作用。
在空气弹簧完全充气与完全失气时,气囊内压力及空簧高度见表2。根据LMS 软件的多参考点最小二乘复频域法(PolyMax),识别出车体1 阶垂向弯曲频率见表2。

表2 空簧状态与1 阶垂向弯曲频率关系
空气弹簧刚度与气囊压强、受力载荷、附加空气室容积等因素有关。在其他因素不变的前提下,空簧气囊压强越大,刚度越大。空簧从完全充气到完全失气状态,压强减小,刚度变小,相应的1阶垂弯频率有所下降。
5 结 论
(1)通过数值计算,随着支撑刚度ks的增大,1阶垂向弯曲频率f逐步增大,但增加十分有限,当刚度增加10 倍时,垂弯频率仅仅增加0.6 Hz 左右。
(2)通过有限元仿真,随着支撑刚度ks的增大,1 阶垂向弯曲频率呈缓慢增加趋势,但增加幅度非常小,当刚度增加10 倍时,垂弯频率仅仅增加0.2 Hz 左右。支撑刚度的增加与自由模态及无约束模态相差甚微。通过比较有限元及数值计算结果,车体1 阶垂向弯曲频率非常接近,将车体简化为欧拉梁,模型正确,结果可靠,工程中可以采用。
(3)在其他因素基本不变的前提下,空簧气囊压强越大,空簧刚度越大。空簧从完全充气到完全失气状态,压强减小,刚度变小,相应的1 阶垂弯频率有所下降。
通过数值计算、有限元仿真以及现场模态试验可以得出:随着支撑刚度的增加,车体1 阶垂向弯曲频率呈缓慢增加趋势;支撑刚度对车体1 阶垂向弯曲频率影响不大。

