中低速磁浮列车系统振动响应的非线性度分析

陈双喜

（成都大学 机械工程学院， 成都610106）

和轮轨列车不同，磁悬浮列车的推进、悬浮和导向功能均由电磁力来完成。当电磁铁提供最大悬浮时，磁铁处在力与距离特性曲线的非线性部分［1］。由于工作环境复杂，负载变化大，磁浮列车需要控制能力强的非线性控制系统。因此，磁悬浮列车动力学系统与控制系统具有显著的非线性特征。磁浮车在运行过程中，悬浮间隙会出现极限环运动、多频率耦合、悬浮失稳振动等动力学行为，如果进行线性化处理，这些复杂的现象就会被忽略。国防科大的CMS 试验车在试验中曾被观察到因为控制环节非线性时滞导致的车轨共振现象。武建军等在研究磁浮车动力学特性时发现了非线性混沌现象［2］。可见，如果忽略系统中的非线性环节可能导致完全不同的动力学行为［3-5］。因此，研究磁浮列车系统振动的非线性问题具有重要的理论和实际意义。

西南交通大学赵春发建立了常温超导磁浮列车动力学模型，并提出了性能评价方法［6］。国防科技大学施晓红建立了基于刚性轨道的悬浮控制器模型和电磁铁模块的悬浮车轨耦合系统模型［7］。王洪坡从非线性动力学和结构动力学2 方面着手，揭示了车轨耦合系统的动态本质［8］。国防科大赵春霞通过数学建模与仿真的方法建立了列车沿轨道匀速运行时车辆系统的导向动力学模型［9］，对车辆系统和线路系统的结构进行了参数化。陈强将系统误差变量引入PID 控制系统，生成非线性PID控制算法，改善了跟踪设定值与控制挠动之间的矛盾［10］。国防科大刘耀宗建立了包含闭环控制在内的悬浮架动力学方程，仿真分析单点扰动时各个闭环悬浮系统的稳态响应［11］。国防科大贺光建立了中速磁浮列车整车动力学模型，研究了200 km/h中速磁浮列车的导向能力［12］。同济大学孙友刚针对单点悬浮系统的非线性、时变性，提出了一种滑模控制方法［13］。王连春提出了基于磁通导数反馈的磁浮列车—钢梁耦合共振抑制算法［14］。

目前磁浮车耦合动力学特性研究一个重要方向是研究耦合系统的非线性振动特性。由于非线性振动学理论发展还不完善，许多问题还无法进行理论计算分析，而数值计算方法的发展和计算机性能的提高使数值仿真分析成为可能。非线性振动信号通常包含频率调制或幅值调制成分，美籍华人Huang 提出了基于信号的调制现象定义振动非线性度［15］。文中根据磁浮列车—轨道—桥梁耦合动力学理论建立典型的中低速磁浮列车动力学模型，计算不同控制参数下车辆系统的振动响应，并将非线性度指标计算方法引入仿真数据的分析中，研究控制参数对车辆振动信号非线性程度的影响规律。

1 中低速磁悬浮列车模型

1.1 磁浮列车动力学模型

文中建立典型的中低速磁浮车辆—轨道—桥梁耦合动力学模型，如图1 所示。单节磁浮车有3个磁浮转向架，转向架左右2 个悬浮导向模块通过防侧滚梁连接，相同悬浮模块的悬浮电磁力共用1个控制器。转向架与车体之间通过空气弹簧连接，而导向结构采用类似日本HSST-100 磁浮车的装置。建立的磁浮车模型包括1 个车体、3 个转向架（6 个悬浮模块），每个部件具有5 个方向的运动自由度（沉浮、横移、点头、摇头、侧滚），整车一共35 个自由度。

图1 中低速磁浮车—轨道—桥梁耦合动力学模型

车体垂向运动zc、横向运动yc、点头运动φc、摇头 运 动ψc、侧 滚 运 动θc微 分 方 程 分 别 为 式（1）～式（5）：

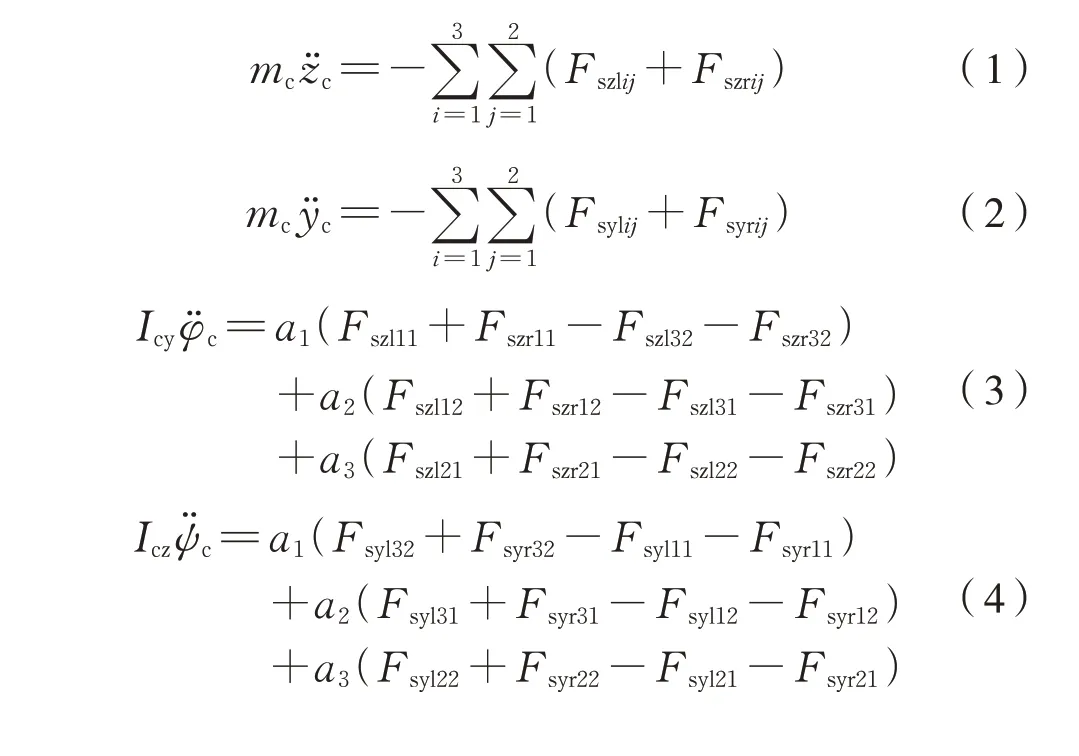
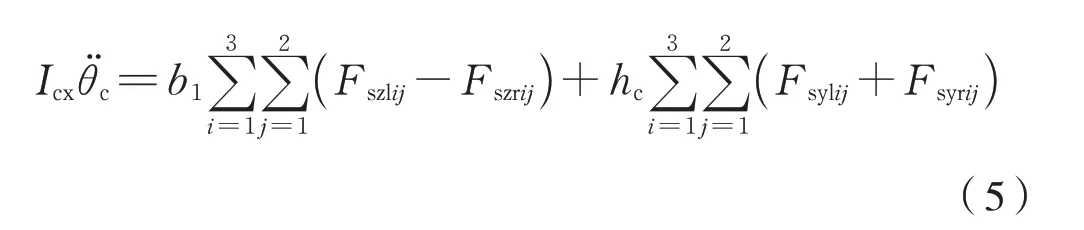
第i个转向架单侧悬浮块的垂向运动zb、横向运 动yb、点 头 运 动φb、摇 头 运 动ψb、侧 滚 运 动θb运动微分方程分别为式（6）～式（10）：

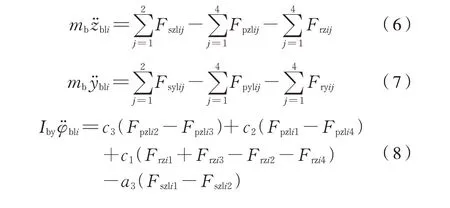
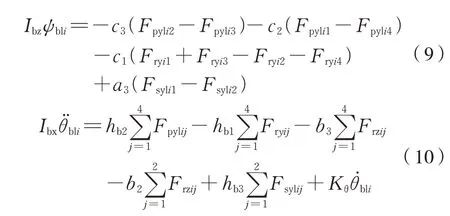
式 中：mc为 车 体 质 量；Icx、Icy、Icz分 别 为 车 体 侧 滚、点头、摇头转动惯量；mb为转向架悬浮模块质量；Ibx、Iby、Ibz分别为转向架悬浮模块侧滚、点头、摇头转动惯量；Fszl(r)ij、Fsyl(r)ij分别为二系悬挂垂向力、横向 力；Fpzl(r)ij、Fpyl(r)ij分 别 电 磁 垂 向 力、横 向 力；Frzij、Fryij分别为单个转向架防侧滚梁铰点垂向力、横向力；Kθ是电磁铁侧滚刚度。其他参数为车辆的几何结构参数。

1.2 高架桥梁模型

磁悬浮轨道高架桥梁通常采用混凝土简支梁结构，先在工厂制造出单跨梁，然后现场组装或者焊接成连续梁。高架桥梁高跨比和宽跨比通常都很小，从材料力学角度考虑都归结为细长梁，在低频振动时候完全可忽略其剪切变形和截面绕中性轴转动惯量。因此，高架桥梁完全可采用Bernoulli-Euler 简支梁模型来描述。磁浮高架桥梁的微分方程为式（11）、式（12）：

式中：EI为梁的垂向抗弯刚度；c为梁的阻尼；ms为梁的线密度；fi(t)为外力；ym、ygi分别为梁上作用点位移及其转向架上对应点的位移；φn(x)为梁的n阶 模 态 函 数；qn(t)为n阶 模 态 广 义 幅 值；kb、cb分别为磁隙刚度、阻尼。

1.3 磁浮系统悬浮控制模型

根据电磁学理论，在不考虑磁阻和漏磁情况下，单个模块悬浮电磁铁系统的耦合方程组为式（13）～式（15），式（13）～式（15）分别是力学、电学和关联方程。

式中：mb为电磁铁悬浮质量；Fmb为电磁力；Fp为外部干扰力；u、i为电磁铁电压、电流；N为线圈匝数；R0为线圈电阻；A为磁铁有效磁极面积；δ为悬浮间隙；μ0为真空磁导率；zb为电磁铁垂向位移。

中低速磁浮列车一般两级串联悬浮控制系统，其控制电压来自悬浮块两端的传感器。假定电磁与控制电路处于理想状态，则悬浮电磁铁PID控制的数学模型为式（16）：

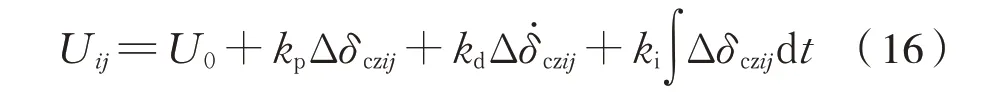
式中：kp、kd、ki分别为悬浮间隙比例、微分和积分反馈控制系数；Δδczij、δ˙czij分别为悬浮间隙和间隙导数控制信号。

2 振动信号非线性度计算方法

根据线性代数理论，线性系统是一个状态量和输出量对所有输入量、初始状态都能满足叠加、放大原理的系统。该准则依赖系统的初始条件和载荷情况，这种系统现实中很少存在，这是因为现实中的系统比理想要复杂得多，输入输出量很难量化。Huang［15］提出了基于振动信号的波内调制现象来量化信号的非线性程度，即式（17）：

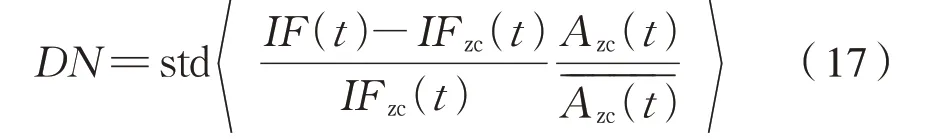
式中：std 表示求标准差；IF(t)为瞬时频率；IFzc(t)为过零点频率；Azc(t)为零点频率对应的幅值。瞬时频率的计算通常采用正交化Hilbert 变换或者DQ 变换［16］。文中采用DQ 变换方法。

3 磁浮车振动响应非线性度分析

假定磁浮列车运行在直线高架桥梁轨道上，列车运行速度v为100 km/h；车体质量12 000 kg；车体侧滚、点头、摇头转动惯量Icx=2 500 kg·m2、Icy=150 000 kg·m2、Icz=150 000 kg·m2；模 块 质 量1 000 kg；模块侧滚、点头、摇头转动惯量分别为Ibx=100 kg·m2、Iby=1 200 kg·m2、Ibz=1 200 kg·m2；二系悬挂垂向、横向刚度分别为120 000 N·m、25 000 N·m；二系阻尼分别为60 000 N·s/m、40 000 N·s/m；抗侧滚梁垂向、横向刚度分别为10 000 N·m、1 000 N·m；桥梁设定为12 跨，总长288 m。桥梁单跨24 m；抗弯刚度EI=2.456×1010N·m2；线密度m=3 755 kg/m。

磁浮线路的周期性不平顺表示为式（18）：

式中：z0=Az为不平顺幅值；λz为波长。仿真分析中，设定轨道不平顺波长为24 m，幅值为2 mm。

悬浮电磁铁长度840 mm，磁极宽度28 mm，线圈匝数为320，磁导率μ0=4π×10-7，名义悬浮间隙10 mm，等效输出电阻1 Ω。电磁铁侧滚刚度Kθ= 4×105N·m/rad。每个电磁铁上集中力数量为4。悬浮系统采用PID 控制方式，反馈控制系数kp、kd、ki取 值 范 围 分 别 为3 000～50 000、200～1 000、0.1～20。磁浮车辆—高架桥耦合系统动力学问题可采用中心差分法和龙格库塔法求解，但求解速度较慢，文中采用翟婉明院士提出的一种快速显式积分法［17］。

在设定参数下，磁浮车典型的动力学响应计算结果如图2 所示。图中实线是悬浮模块的振动加速度，虚线是车体的振动加速度。可以看出，悬浮模块振动加速度大于车体，两者均为1 个低频振荡承载着在载波上下波动的高频振荡，振动信号具有显著的非线性特征。

对图2 的振动加速度进行经验模态分解得到本征模态函数，然后求瞬时频率IF(t)和过零点频率IFzc(t)（幅值Azc(t)），运用式（17）计算振动信号的非线性度DN。磁浮列车在典型PID 控制方式下，控制参数对车辆振动非线性度的影响如下。

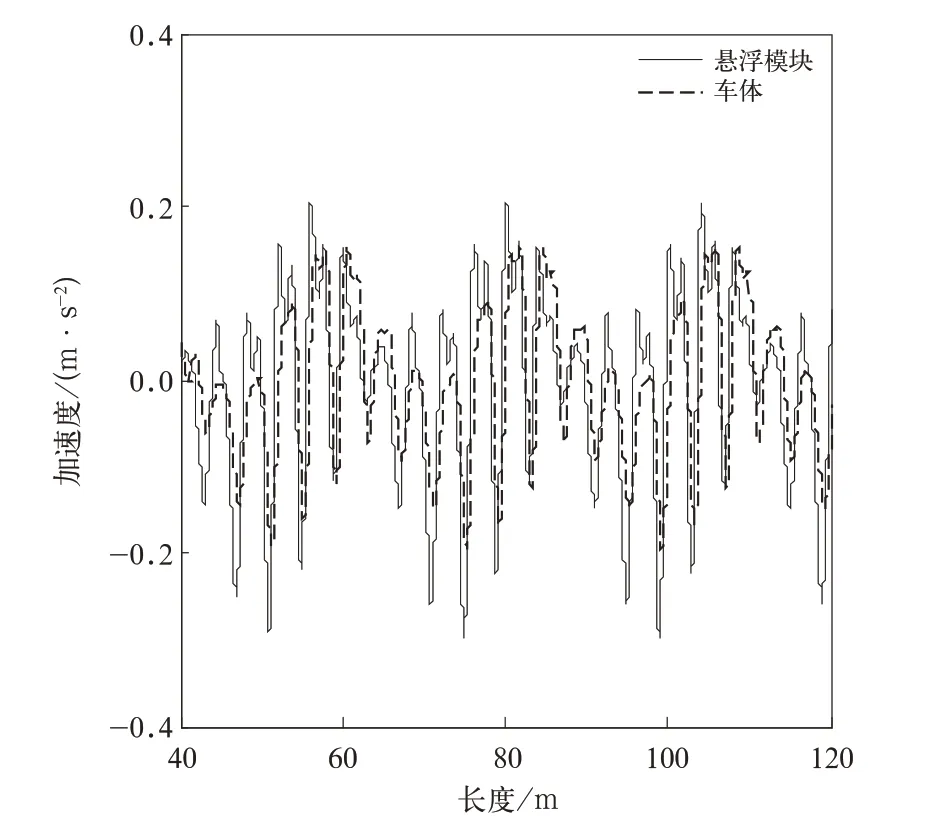
图2 车体与悬浮模块垂向振动加速度

3.1 控制参数kp 对振动非线性度的影响

悬浮控制参数kp是比例反馈系数，成比例地反映控制系统悬浮间隙的偏差信号Δδczij，偏差一旦产生，立即产生控制作用以减小偏差。由偏差理论知，增大kp虽然可以减小偏差，但不能彻底消除偏差。比例控制系数kp作用的大小除与偏差Δδczij有关之外，还取决于比例系数kp的大小。比例系数kp越小，控制作用越小，系统响应越慢；反之，比例系数kp越大，控制作用也越强，则系统响应越快。当kp在3 000～50 000 范围内，磁浮车车体、悬浮模块的垂向振动响应的非线性度随参数变化情况如图3、图4 所示。当kp=3 000 时，车体振动DN最大值0.32，非线性程度很大；当kp＞30 000 时，DN减 小 到0.1 以 下，非 线 性 程 度 大幅度减小。总体上，车体、悬浮块垂向振动非线性度DN随kp增 大 而 减 小，且 当3 000＜kp＜10 000，DN下降幅度比kp＞10 000 时大。因此，合理范围内增大比例系数kp，不仅可以增强控制作用，加快系统响应，而且可以降低振动响应的非线性程度。

图3 kp 对车体垂向振动非线性度DN 影响

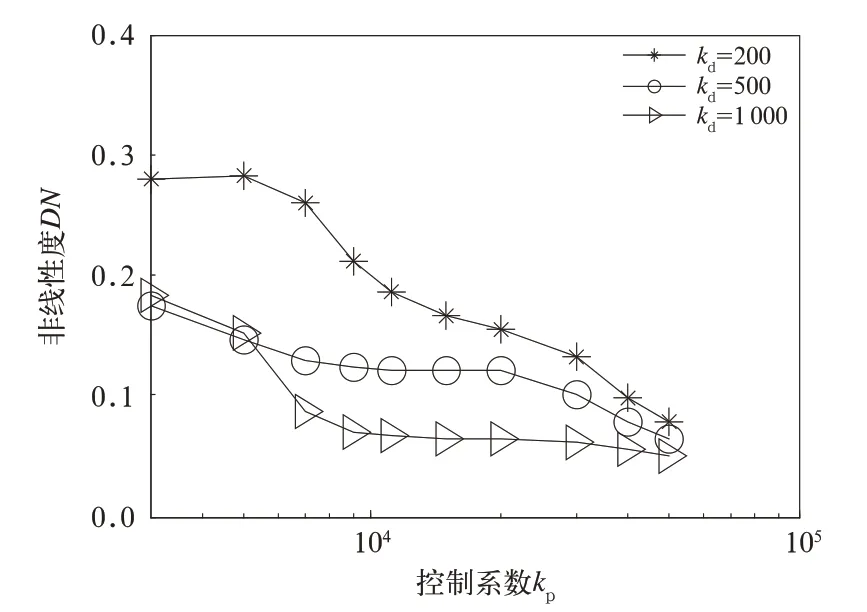
图4 kp 对模块垂向振动非线性度DN 影响

3.2 控制系数kd 对振动非线性度的影响

磁浮PID 控制系统微分环节的作用是反映磁浮间隙偏差信号的变化速率δ˙czij，并在间隙偏差信号Δδczij变得太大之前引入1 个有效的修正信号，从而加快系统的动作速度。微分输出只与偏差的变化速度δ˙czij有关，而与磁浮间隙偏差Δδczij的大小以及偏差是否存在无关。如果磁浮间隙偏差Δδczij为固定值，不管多大，只要不变化，则输出的变化一定为0，磁浮控制器没有任何控制作用。合理的微分控制系数kd有助于克服振荡，改善系统的动态性能。设定kp和ki为固定值（设定kp=7 000，ki=10），分析kd对振动非线性度的影响。当kd在200～1 000 范围内，磁浮车车体、悬浮模块的垂向振动响应的非线性度随参数变化情况如图5 所示。当kd=200，模块、车体振动DN最大值分别为0.26、0.20，具 有 较 大 非 线 性 度；当kd=1 000，模块、车体振动DN分别减小到0.08、0.07，非线性程度大幅度减小。总体上，车体、悬浮块垂向振动非线性度DN随kd增大而迅速减小。

图5 kd 对车体与模块垂向振动非线性度DN 影响

3.3 控制系数ki 对振动非线性度的影响

磁浮PID 控制系统积分环节中，控制器的输出与输入误差信号Δδczij的积分成正比关系。积分控制作用的存在与偏差Δδczij的存在时间有关，只要磁浮间隙存在着偏差，积分环节就会不断起作用，对输入偏差Δδczij进行积分，使控制器的输出和执行器的开度不断变化，产生控制作用以减小悬浮间隙偏差。当积分控制系数ki在0.1～20 范围内，磁悬浮模块的垂向振动响应的非线性度随参数变化情况如图6 所示。当ki=0.1，模块振动DN最大值为0.309，具有较大非线性度；当ki=20，模块振动DN最小为0.302，非线性程度几乎没有变化。计算结果表明：积分控制系数ki对车体、悬浮块垂向振动非线性度DN几乎没有影响，系统振动响应的非线性程度并不会随着ki增加而明显减小。

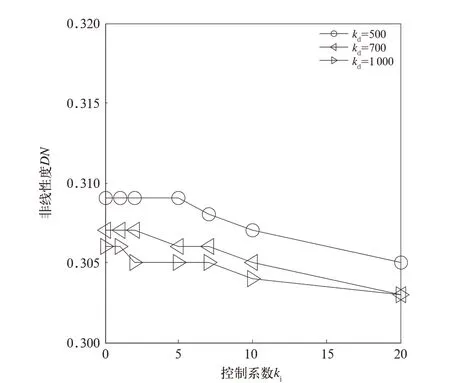
图6 ki 对车体与模块垂向振动响应非线性度DN 影响

4 结 论

根据磁浮列车车辆—轨道—桥梁耦合动力学理论建立典型的中低速磁浮列车模型，计算不同控制参数下车辆系统的振动响应，并将非线性度指标计算方法引入仿真数据的分析中，研究磁浮控制系统参数对车辆振动信号非线性度的影响规律。通过仿真分析得到如下结论：

磁浮列车PID 控制系统的比例反馈系数kp和微分反馈系数kd对车辆系统振动响应非线性度DN有很大影响。kp、kd较小时，车体、悬浮块振动信号具有很强的非线性特征，但非线性度随kp、kd增大而迅速减小。积分反馈系数ki对车体、悬浮块振动非线性度影响很小，几乎不会改变磁浮车辆动力学系统的强非线性特征。从降低振动非线性度方面考虑，可给出一组优化的控制参数：kp=10 000，kd=1 000，ki=10。