大功率制动盘紧固连接设计及拧紧技术研究*

曹建行

（1 北京纵横机电科技有限公司， 北京100094;2 中国铁道科学研究院集团有限公司 高速铁路与城轨交通系统技术国家工程研究中心， 北京100081）

随着高速动车组运营速度的提高，特别是“复兴号”系列动车组的批量运营，列车的制动可靠性成为了轨道交通行业关注的重点。制动盘作为高速动车组制动系统的关键部件，制动功率大，运用工况复杂，其紧固件连接性能对列车制动盘的可靠性起着至关重要的作用［1-2］。

高速列车轮装制动盘为法兰式圆盘状结构，由多颗螺栓连接到轮辐两侧。紧固螺栓安装预紧力的准确性和一致性是决定产品紧固性能的重要因素，也是评价产品安装质量的重要指标［3］。但高速列车轮装制动盘的运用工况复杂，产品结构紧凑，螺栓预紧力的精细化设计成为了制动盘开发过程中的难点问题；同时，在当前传统扭矩法的拧紧工艺下，紧固件摩擦系数的离散性会影响安装预紧力的精确控制［4-5］。文中深入研究制动盘的紧固技术，以VDI2230 高强度螺栓连接理论（以下简称“VDI2230 理论”）为基础，建立适用于轮装制动盘的紧固连接计算模型，确定螺栓目标预紧力；针对工业生产中制动盘螺栓安装预紧力的控制要求，开发轮装制动盘扭矩—转角法组装工艺。提高工业化生产中制动盘螺栓预紧力的准确性和一致性，达到提升制动盘可靠性的目的。

1 紧固连接计算

以某型号速度350 km/h 高速动车组轮装制动盘为研究对象，研究紧固连接理论，建立紧固连接计算模型，确定螺栓目标预紧力。 该计算以VDI2230 理论为基础，结合轮装制动盘的结构特点及服役特性，对制动盘螺栓进行紧固分析。

轮装制动盘由螺栓和螺母把盘体紧固连接到轮辐两侧，如图1 所示。列车制动时，闸片与制动盘摩擦对车轮产生制动扭矩。列车制动过程中将动能转化成热能，摩擦制动产生的热能被制动盘储存并逐步传递到车轮和空气中［6-8］。制动过程中，制动盘螺栓需要提供满足制动扭矩所需的最小夹紧力，需要考虑由于微观嵌入作用和温度变化引起的预紧力损失，考虑工作载荷对螺栓轴力的影响［9］。

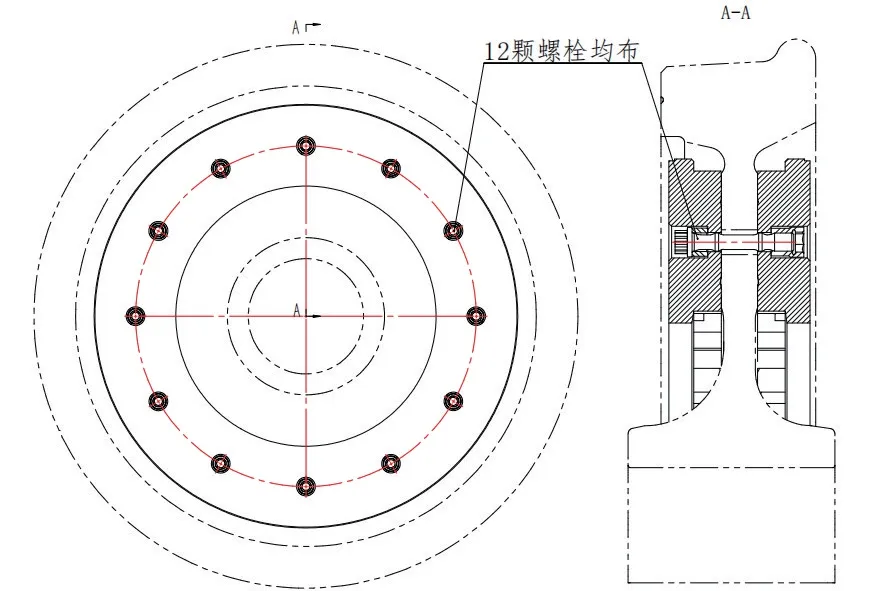
图1 轮装制动盘结构示意图

1.1 受力模型

根据轮装制动盘的结构特点，将法兰结构多螺栓连接问题简化为同心夹紧和同心加载的单螺栓连接问题，建立螺栓的受力模型［10］。连接结构的简化模型如图2 所示，连接结构受力模型如图3所示。

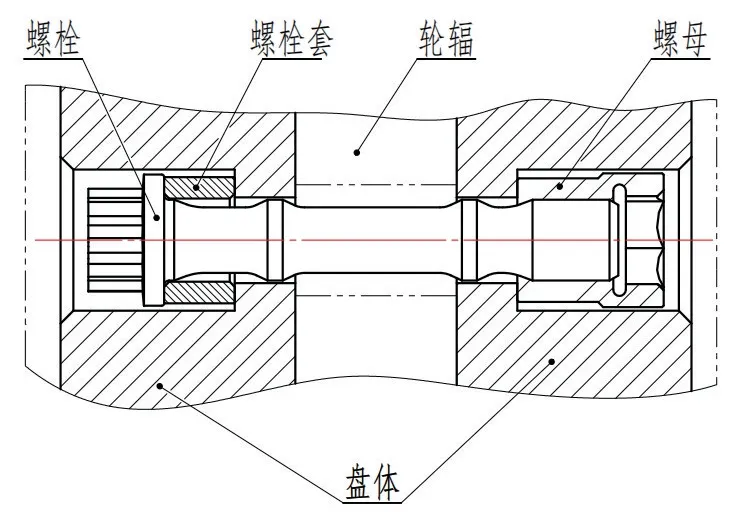
图2 螺栓连接简化模型

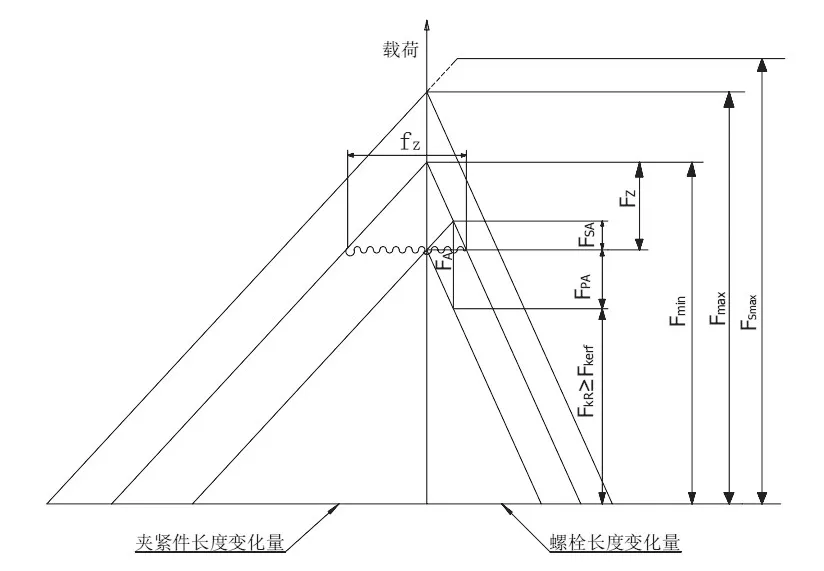
图3 螺栓的受力模型

1.2 校核计算

1.2.1 确定最小夹紧力

制动盘螺栓需要提供满足制动扭矩所需的最小夹紧力FKerf为式（1）：

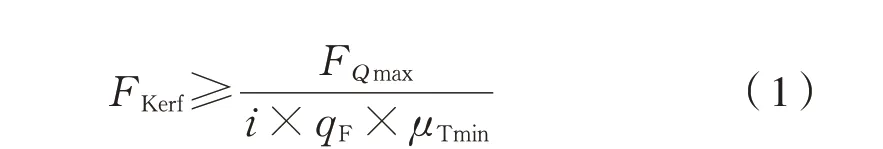
式中：FKerf为最小夹紧力；FQmax为螺栓横向载荷；i为螺栓数量；qF为分界面数量；μTmin为分界面间的最小摩擦系数。

1.2.2 确定工作载荷

列车高速运行过程中，制动盘承受频繁振动冲击力FA1，列车高速制动过程中，螺栓承受盘体热膨胀带来的热载荷FA2。

则螺栓附加工作载荷为式（2）：

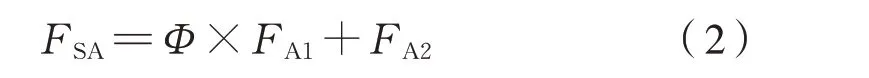
式中：Φ为载荷系数。

由于振动冲击引起的夹紧件附加工作载荷为式（3）：

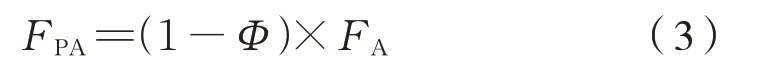
紧固连接模型的载荷系数为式（4）：

式中：δp为夹紧件的柔度；δs为螺栓的柔度。

1.2.3 确定预紧力的变化量

各分界面和螺纹间的微观压溃会导致螺栓安装预紧力的衰减，安装预紧力的衰减量为式（5）：

式中：fZ为微观压溃量。

由于制动盘螺栓和夹紧件具有不同的热膨胀系数，当制动过程中温度发生变化时，安装预紧力会发生衰减，衰减量为式（6）：

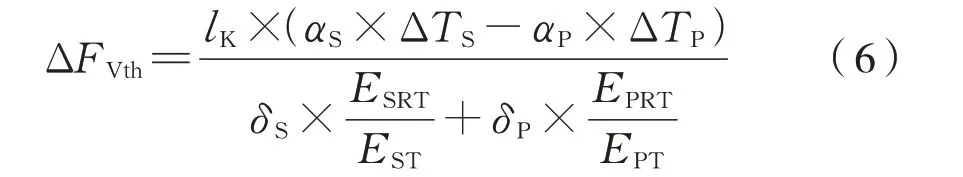
式中：lK为夹紧长度；ΔTS为螺栓的温度变化量；ΔTP为夹紧件的温度变化量；ESRT为螺栓室温弹性模量；EST为螺栓工作温度下弹性模量；EPRT为夹紧件室温弹性模量；EPT为夹紧件工作温度下弹性模量。

1.2.4 确定安装预紧力

考虑到制动盘工作过程中安装预紧力的变化量和工作载荷对螺栓轴力的影响，结合满足制动扭矩所需的最小夹紧力，可以确定制动盘螺栓的最小安装预紧力为式（7）：

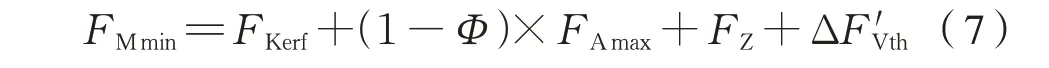
确定最大安装预紧力为式（8）：

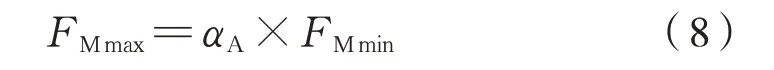
式中：αA为拧紧系数。

1.2.5 校核螺栓的安装预紧力

螺栓所允许的最大安装预紧力为式（9）：

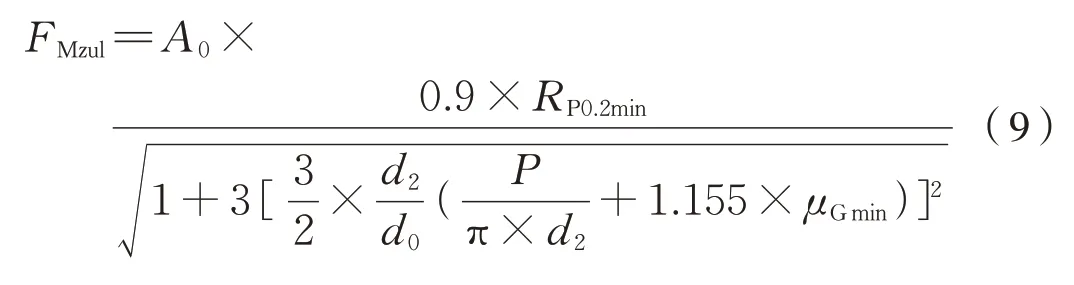
式中：A0为螺栓最小横截面积；RP0.2min为螺栓最小屈服强度；μG为螺纹间摩擦系数；P为螺距；d0为螺栓最小直径；d2为螺栓的螺纹中径。

螺栓安装预紧力需满足FMmax≤FMzul。

1.2.6 校核螺栓的工作应力

螺栓的最大轴向载荷为式（10）：

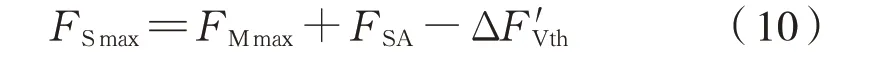
螺栓最大拉应力为式（11）：

螺栓最大扭转剪切应力为式（12）：

其中，

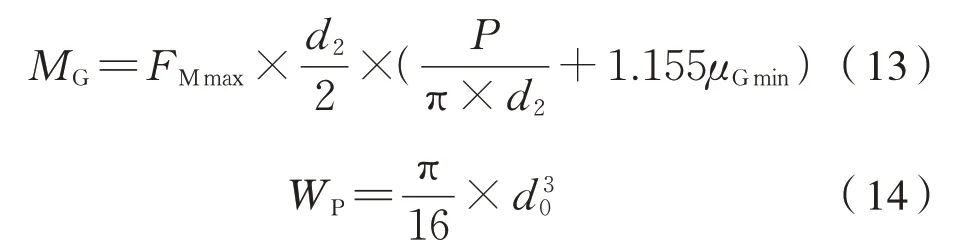
螺栓最大等效应力为式（15）：

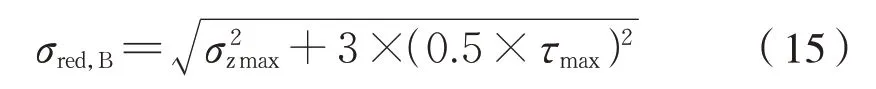
螺栓工作应力安全系数需满足式（16）：

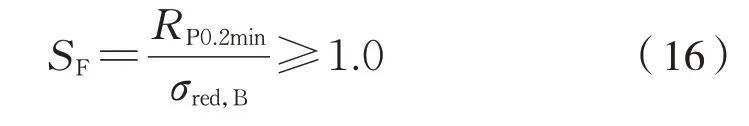
1.2.7 校核螺栓的交变应力

连接螺栓交变应力幅为式（17）：

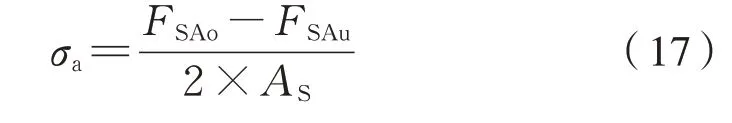
式中：FSAo为最大轴向附加载荷；FSAu为轴向最小附加载荷；AS为螺纹应力截面积。

高强螺栓关于应力截面AS的疲劳极限在ND≥2×106交变次数的参考值：

热处理前滚丝（SV）为式（18）：

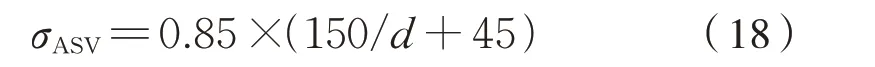
热处理后滚丝（SG）为式（19）：

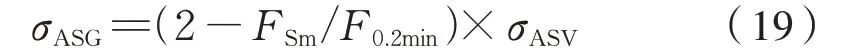
式中：d为螺栓螺纹公称直径；FSm螺栓平均载荷；F0.2min为螺栓最小屈服载荷。

螺栓交变应力安全系数需满足以下要求为式（20）：

1.2.8 校核表面抗压强度

表面抗压强度需满足以下要求：

式中：pMmax为装配状态表面最大压应力；pBmax为工作状态表面最大压应力；Ap为螺栓或螺母支承面积；pG螺栓、螺母或垫圈的最大许用压应力。

1.2.9 校核抗滑移能力

紧固连接模型中，螺栓的横向载荷需要承担制动扭矩，因此：

最小残余夹紧力：FKRmin=FKerf

承担横向载荷所需的最小夹紧力为式（21）：

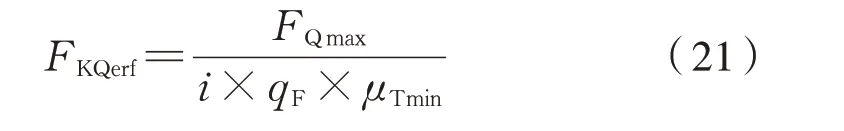
抗滑移安全系数需满足如下要求为式（22）：

1.3 结果分析

按照建立的计算模型，结合制动盘的运用工况，对制动盘螺栓的安装预紧力进行校核计算，计算结果见表1。

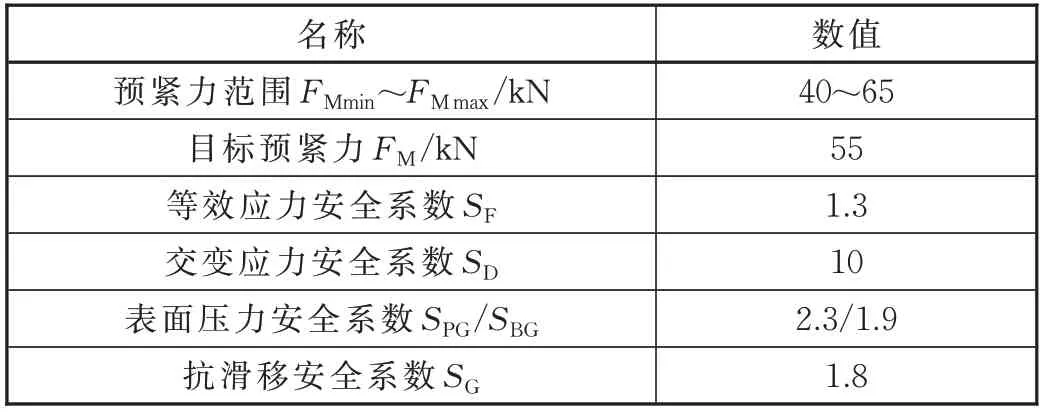
表1 计算结果

从计算结果可以看出，满足运用要求的预紧力 控 制 范 围 在40～65 kN 之 间，该 范 围 内，SF、SD、SPG、SBG、SG大于等于1.0。各项安全系数满足运用要求。考虑装配过程中安装预紧力的离散性，确定扭矩—转角法工艺开发过程中螺栓的目标预紧力为55 kN。

2 工艺参数研究

通过扭拉试验，研究紧固件的扭拉特性，探索初步的扭矩—转角法组装工艺参数。试验室扭拉特性测试设备为Schatz 卧式拧紧试验机。

2.1 扭拉试验

考虑到螺纹配合界面间摩擦系数、毛刺、凸起等离散性因素的影响，试验时先对螺母施加一定预紧扭矩，然后再拧松螺母，对螺纹进行磨合，最后按目标预紧力进行扭拉测试试验。取5 套紧固件作为试验样本进行测试，试验结果如图4 所示。

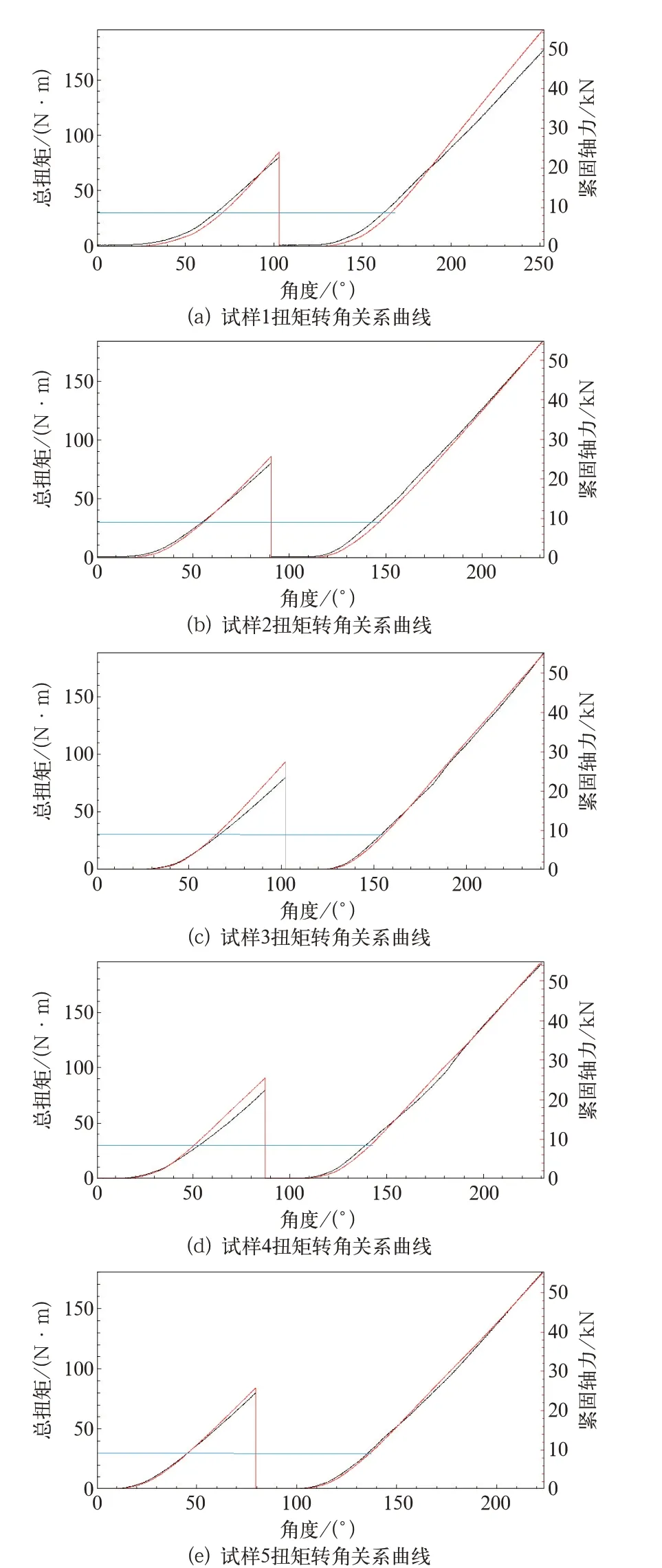
图4 试验样本扭矩转角关系曲线

贴紧扭矩达到30 N·m 时，试验螺栓扭拉关系曲线全部进入线性段，表明紧固件已经完全贴合。考虑到拧紧时摩擦系数具有一定的离散性，为了保证所有螺栓均完全贴合，贴紧扭矩通常为试验值的1.3 倍，因此初步确定贴紧扭矩为40 N·m。拧紧试验过程中，扭矩达到4 N·m 时，开始记录扭转角度，当螺栓轴力达到目标预紧力时，各试验样本的扭矩转角度见表2，扭转角度均值为79.5°。确定初步的工艺参数为40 N·m+79.5°。

表2 扭转角度 单位：（°）

2.2 参数修正

试验室扭拉试验机的夹紧层材料为铝合金，制动盘的实际夹紧层材料为铸钢，分析对比2 种夹层材料的弹性模量，见表3。由表3 可知，扭拉试验机的夹层刚度小于制动盘的夹层刚度。因此采用扭矩转角法进行组装时，扭拉试验测得的扭转角度要大于实际组装过程中的扭转角度。有必要对扭拉试验测得的扭转角度进行修正。

表3 夹紧层材料弹性模量 单位：GPa

扭矩—转角法是在组装过程中螺纹紧固件达到规定的起始扭矩后，再转动螺纹件达到目标角度的一种紧固件安装方法［11］。具体原理为：螺纹副相对转动一定的角位移后使螺栓产生一定的轴向伸长量，从而产生轴向预紧力。根据扭矩—转角法的拧紧原理建立螺栓的受力三角形模型，如图5 所示。

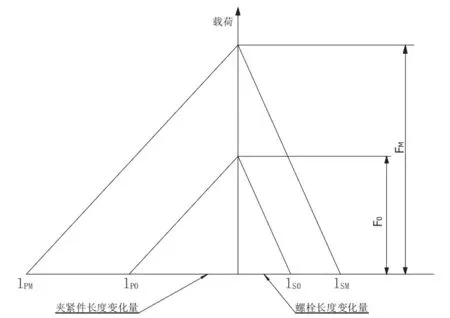
图5 扭矩—转角法拧紧过程螺栓受力三角形

由图5 可以看出，拧紧螺母达到贴紧扭矩40 N·m 时，螺栓轴力 为F0，螺栓变形量为lS0，夹紧件的变形量为lP0。当不停顿继续拧紧，并开始记录扭转角度，扭转角度达到λ时，螺栓轴力达到目标预紧力FM，螺栓变形量为lSM，夹紧件变形量为lPM，由此可以得出：

螺栓的弹性变形量为式（23）：

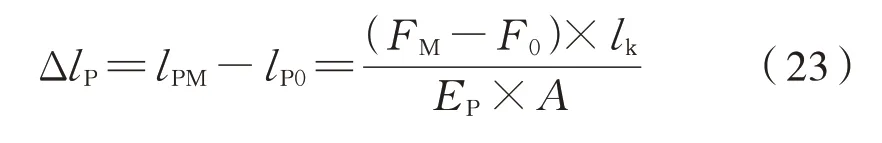
式中：A为螺栓横截面积；EP为夹紧件弹性模量。

夹紧件的弹性变形量为式（24）：

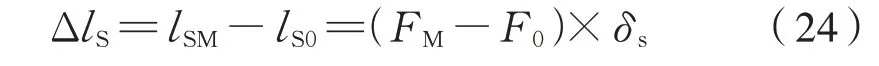
拧紧过程中，螺母的扭转角度转化为螺栓和夹紧件的弹性变形量，由此可以得出式（25）：

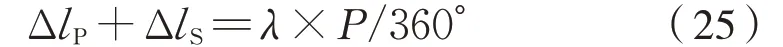
式中：P为螺纹螺距。

由式（23）～（25）可以得出式（26）：

式中：η为修正系数。

结合轮装制动盘的实际工况参数可以得出：修正系数η=0.55，制动盘作为夹紧层时λ钢=43.76°。根据实际组装工况对扭转角度进行取整，从而确定初步的工艺参数为40 N·m+45°。考虑到实际组装条件影响因素较多，该工艺参数还需在工程实践中进行验证。

3 组装验证试验

为了验证试验室扭矩—转角法工艺参数的准确性，确定扭矩—转角法的最终工艺参数，进行组装验证试验。

3.1 试装试验

在组装现场对初步的扭矩—转角工艺参数40 N·m+45°进行试装，试验样本为1 套轮装制动盘（包括12 颗螺栓），组装设备为Atlas 自动拧紧机。组装完成后，采用超声波轴力测试设备对螺栓预紧力进行测试，记录螺栓的预紧力值。

扭矩—转角工艺参数为40 N·m+45°时，试验结果如图6 所示，1 套制动盘12 螺栓共测得8 个有效预紧力值。

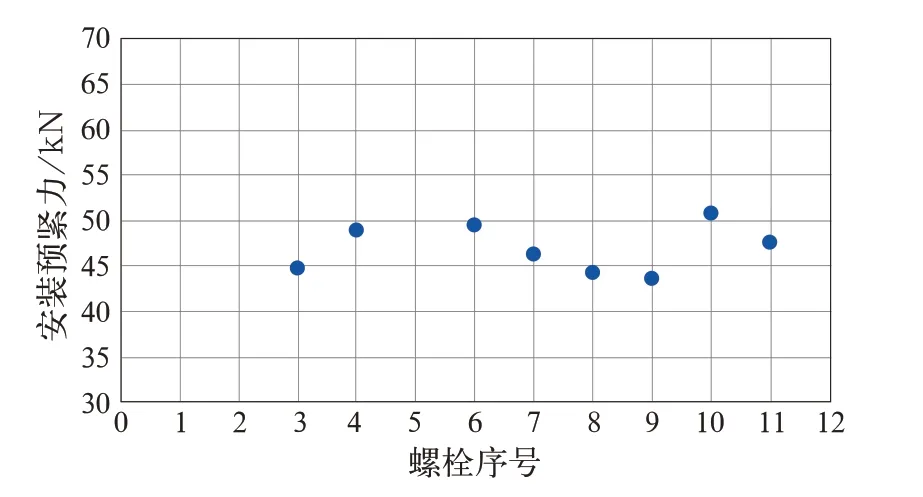
图6 螺栓预紧力分布图

从图6 可以看出，当扭矩—转角工艺组装参数为40 N·m+45°时，测得的安装预紧力均小于目标预紧力，因此该扭矩—转角工艺组装参数不满足工程应用要求，需要对扭转角度进行调整。

3.2 参数调整试验

根据试装情况，增大扭转角度进行参数调整试验，扭矩—转角工艺参数分别为40 N·m+47.5°、40 N·m+50°和40 N·m+52.5°，每个工艺参数试验样本均为1 套轮装制动盘，试验结果如图7 所示。

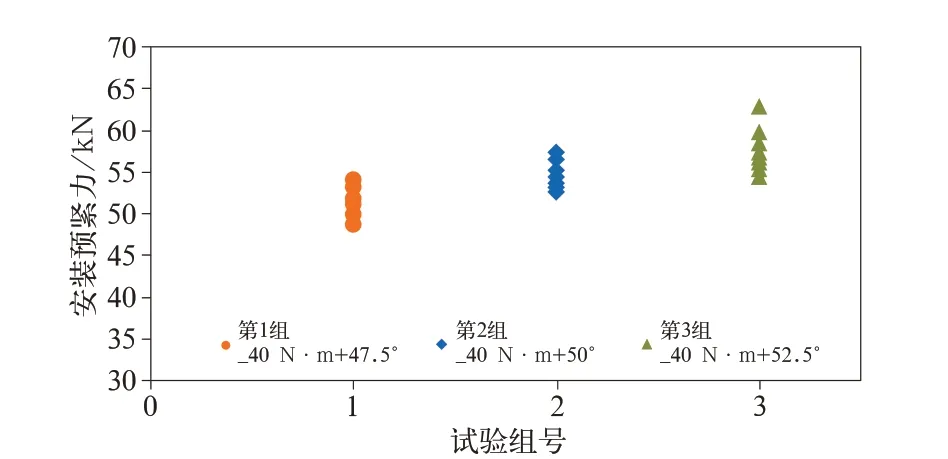
图7 各组螺栓预紧力分布图

由图7 可以看出，第1 组制动盘组装工艺参数为40 N·m+47.5°，安装预紧力范围为48～54 kN，均小于目标预紧力；第2 组制动盘组装工艺参数为40 N·m+50°，安装预紧力范围为52～57 kN，安装预紧力围绕目标预紧力上下波动；第3 组制动盘组装工艺参数为40 N·m+52.5°，安装预紧力范围为54～62 kN，大部分安装预紧力大于目标预紧力。因此确定适用于制动盘组装的扭矩转角工艺参数为40 N·m+50°。

3.3 扩大样本试验

为了验证轮装制动盘扭矩—转角工艺组装参数（40 N·m+50°）的适应性，确定扭矩—转角法组装工艺的监控扭矩，进行扩大样本组装试验，试验样本为4 套制动盘（每套12 颗螺栓），在A、B 2 个不同的组装厂进行试验。具体试验方案：在A 厂组装1 套制动盘，采用相同批次紧固件；在B 厂组装3 套制动盘，其中2 套为相同批次紧固件，1 套为不同批次紧固件。按照上述试验方案进行试验，对螺栓预紧力进行测试，试验结果如图8 所示。

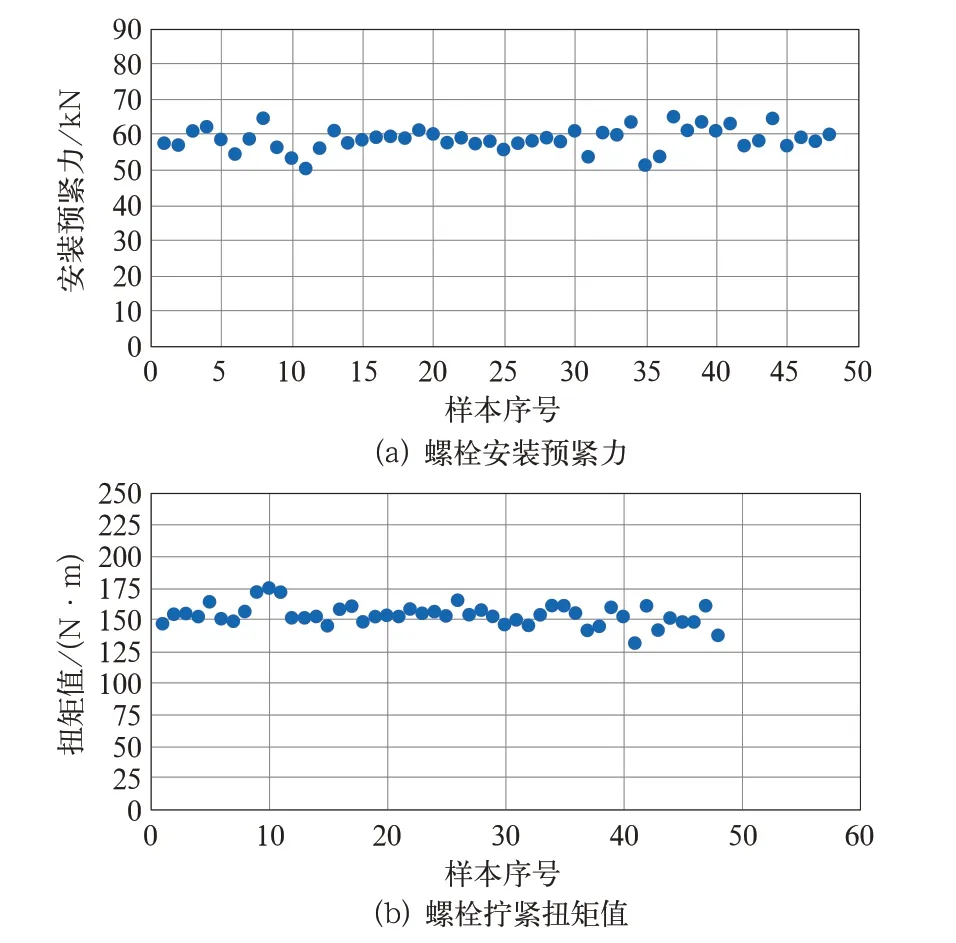
图8 扩大样本试验数据汇总

由图8 中（a）试验结果可以看出，螺栓安装预紧力分布在50～65 kN 之间，围绕目标预紧力55 kN 上下波动，一致性较好，满足预紧力的范围要求，说明扭矩转角工艺参数（40 N·m+50°）合理可行，具有良好的稳定性和适应性。

为了增强扭矩—转角法组装过程中异常件的辨识能力，需要确定合理的扭矩范围，作为制动盘组装过程中的监控扭矩。由图8 中（b）试验结果可以看出，安装扭矩分布在137～175 N·m 之间，安装扭矩一致性较好，考虑到批量组装过程中紧固件摩擦系数的离散性，在试验结果的基础上适当增大监控扭矩范围为130～190 N·m。

4 结 论

文中形成了以紧固连接计算为依据，以扭拉试验结果为基础的紧固件扭矩—转角法组装工艺开发流程。具体结论如下：

（1）基于VDI2230 理论对高速动车组轮装制动盘进行紧固连接计算，建立适用于轮装制动盘的紧固连接计算模型，确定了螺栓目标预紧力。

（2）通过扭拉试验，研究了紧固件的扭拉特性和初步的扭矩—转角工艺参数，提出了以试验为基础的工艺参数修正方法，确定了初步的扭矩—转角法组装工艺参数。

（3）通过工厂验证试验，明确了最终的扭矩—转角工艺参数及监控扭矩，验证了工艺参数的稳定性和适应性，增强了制动盘组装工艺故障件的辨识能力。