基于小波变换的三门峡市年降水序列多时间尺度分析

戴翠贤， 贾 斯， 王 君， 李晓琳

（1.三门峡市气象局，河南三门峡 472000； 2.长垣市气象局，河南长垣 453400； 3.河南省气象学会，郑州 450003；4.中国气象局河南省农业气象保障与应用技术重点开放实验室，郑州 450003； 5.河南省气象科学研究所，郑州 450003）

降水是导致一个地区洪涝、山体滑坡、泥石流等自然灾害发生的首要影响因素，对于农作物种植等也有重要意义. 随着全球气候变暖，洪涝等极端灾害性天气发生的频率和强度也在增大［1-9］，且降水时空分布不均，存在着明显的区域特征［10-12］. 孙杰等［13］研究了华中地区近45 a来的降水变化特征；焦建丽和康雯瑛［14］、苗长明和熊杰伟［15］分析了河南省年、季降水的区域特征；还有些学者对黄河中游三门峡—郑州花园口区间及郑州、开封和临颍降水特征进行了分析［16-20］.

三门峡地处河南、山西、陕西三省交界，年内降水分布不均，降水年际变化大，易发生旱、涝等灾害，严重影响该市农业产业的发展. 分析该市降水变化尺度特征及趋势对预测其短期气候变化，助力农业可持续发展有重要的价值和意义.

小波分析方法［21-22］是通过时频变化突出信号在某些方面的特征，将需要处理的原始信号进行伸缩或平移，从而消除噪音影响和边界效应. 小波分析方法的特点是可直观显示需要分析数据的某一方面特征［23-24］，故可以使用Morlet小波分析方法对数据的周期变化规律和未来趋势进行评估. 本文使用三门峡市气象观测站质控后的1960—2020年降水观测资料进行分析，总结三门峡市降水的气候特征. 首先利用趋势检验对三门峡市近60 a降水时间系列进行趋势分析，然后采用Morlet小波分析方法对三门峡市降水的周期变化规律和未来趋势进行评估.

1 分析方法

1.1 线性分析

一元线性回归拟合曲线：

式中：yt为年份对应降水量；t为时间序列，t=1，2，3，4，…，n；a为常数项；x为年份值；b为回归系数，可以代表降水的气候趋势倾向.b>0，说明y随时间呈现上升趋势；b<0，说明y随时间呈下降趋势.

1.2 小波分析

1.2.1 小波函数

小波函数表达式：

对于给定的有限数据信号f(t)，其连续小波变换为：

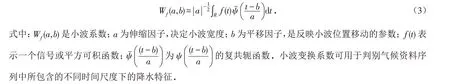
1.2.2 小波方差

将式（3）中Wf(a,b)的平方值在b域上积分，即：

式中：Var(a)为小波方差，小波方差随时间尺度a的变换过程称为小波方差图. 式（4）反映小波信号波动能量随时间a的分布，在降水序列分析中反映不同尺度的降水变化强弱和周期.

1.3 Mann-Kendall突变检验

Mann-Kendall 突变检验是一种气候诊断与预测方法. 应用Mann-Kendall 检验法可以判断气候序列中是否存在气候突变，如果存在，可确定出突变发生的时间.

1）求出UF. 对有n个数值检测分析降水变化趋势以及检测显著性，分析突变点，可用Mann-Kendall方法.计算公式为：

式中：在时间序列随机独立的假定下，定义正系列统计量为UF：

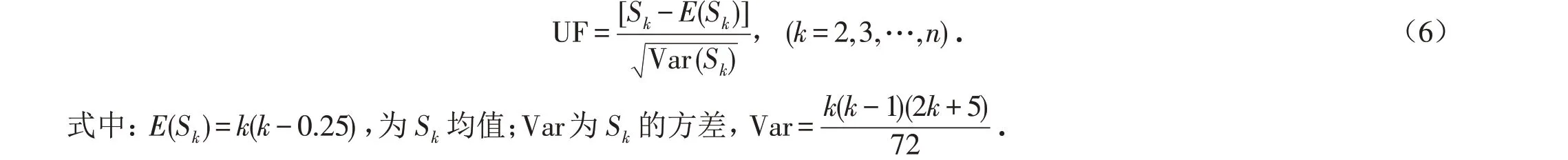
2）将样本进行反向排列，用以上的方法可求出逆序列的统计量UB.

3）根据显著性水平，选定α=0.05，既临界值为±1.96，将UF和UB绘制突变图.

4）分析若UF>0，表示数据呈上升趋势；UF<0，则表示数据为下降趋势；若UF和UB超出临界值，则表明趋势显著.

2 结果与分析

2.1 年降水量趋势分析特征

根据1960—2020年的降水数据和10 a滑动平均进行一元线性回归模拟（图1）. 结果显示，三门峡市年降水量的变化曲线呈不显著下降趋势，没有通过置信度α=0.05的显著性检验，气候倾向率-0.35 mm/10 a，说明三门峡市每10 a降水量约减少0.35 mm.

根据降水数据（图1）分析年降水量为332.6～899.4 mm，年平均降水量552.9 mm. 降水量年际变化很大，最多的年份（2003年）899.4 mm约是降水量最少年份（2001年）332.6 mm的2.7倍.

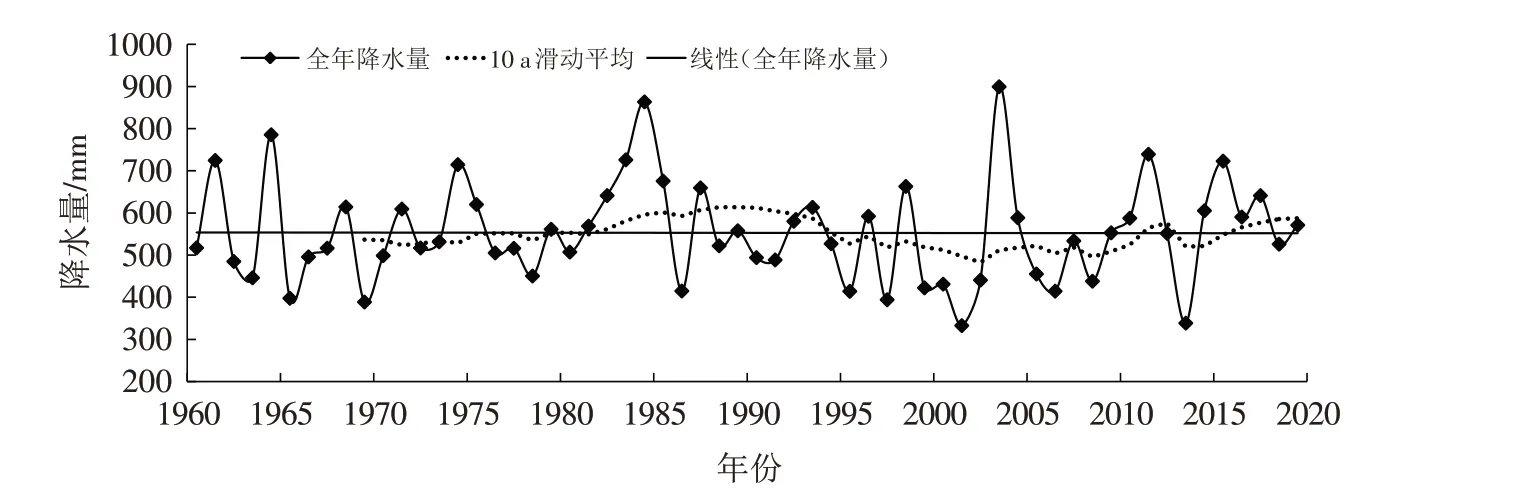
图1 三门峡市1960—2020年降水量回归模拟曲线Fig.1 Regression simulation curve of precipitation from 1960 to 2020 in Sanmenxia City

2.2 降水量变化的小波分析

为了使数据小波分析能够更精确地反映降水变化周期规律，需消除或减少数据序列两端可能产生的“边界效应”. 计算时先使用距平的方法对资料进行预处理［24］，然后将资料向前和向后延拓，变换后再将延拓部分舍弃，保留原数据序列时段的小波系数. 距平变化见图2.

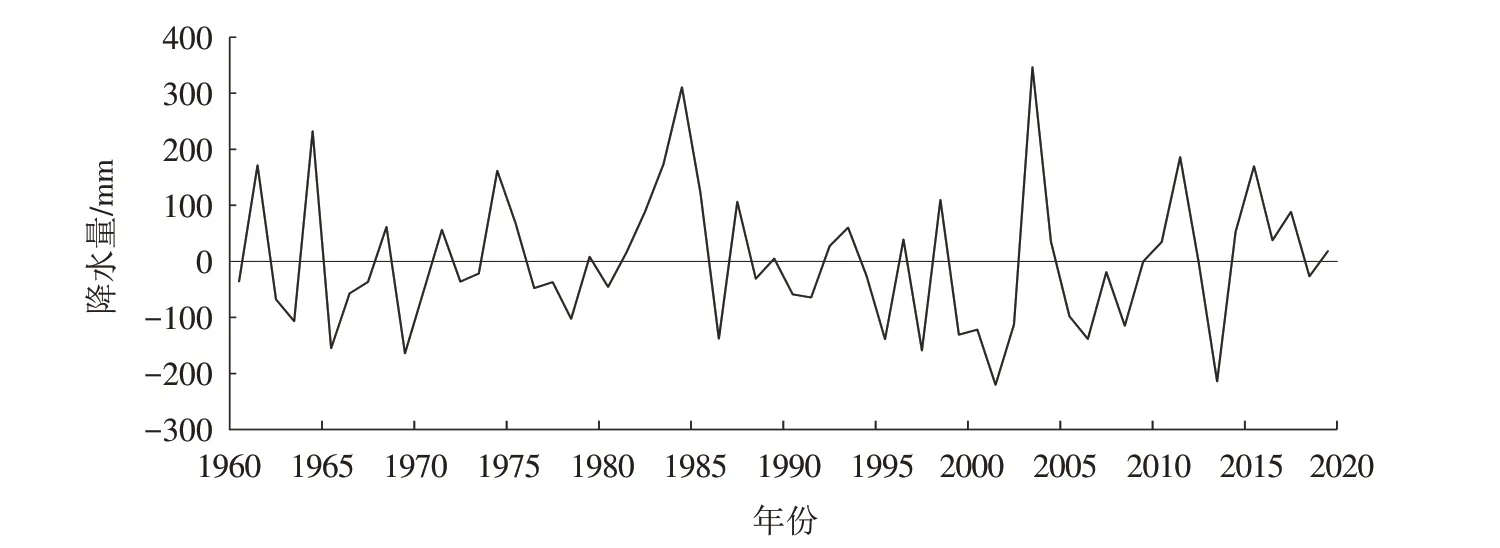
图2 三门峡市1960—2020年降水距平变化曲线Fig.2 Variation curve of precipitation anomaly from 1960 to 2020 in Sanmenxia City

将预处理后的数据做小波系数实部等值线图（图3），图中等值线为小波系数的实部值. 小波系数实部值的正负代表年降水量在该时间尺度上的丰枯，数值的大小反映出丰枯程度，可从数值正负交替震荡的程度判断周期是否明显. 从图3可以看出，12～19 a尺度的周期变化较为明显，正负值差异较大，表现出最大的震荡周期. 而3～7 a前后的周期变化表现比较弱. 总的来说，三门峡市降水量存在着20～32 a、12～19 a、3～7 a三个尺度的变化周期.

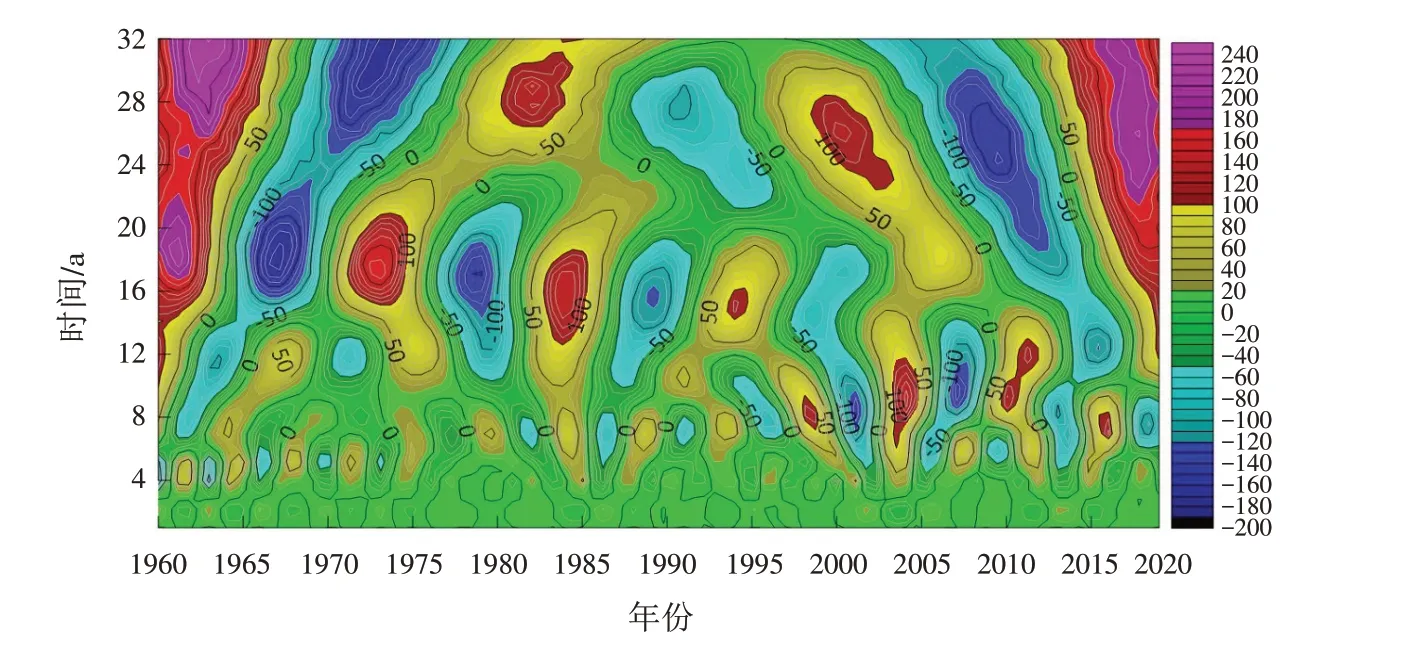
图3 三门峡市降水小波系数实部变换分布图Fig.3 Real part transformation distribution of wavelet coefficients of precipitation in Sanmenxia City

Morlet小波系数的模值是不同时间尺度变化周期所对应的能量密度在时间域中分布的反映，系数模值愈大，表明其所对应时段或尺度的周期性就愈强. 由此，为了分析降水在研究时间尺度的周期性强弱，做出小波系数的模分布图（图4）. 由图可以看出，12～17 a尺度的能量密度最大，其次是能量密度较大的3～10 a前后时间尺度.

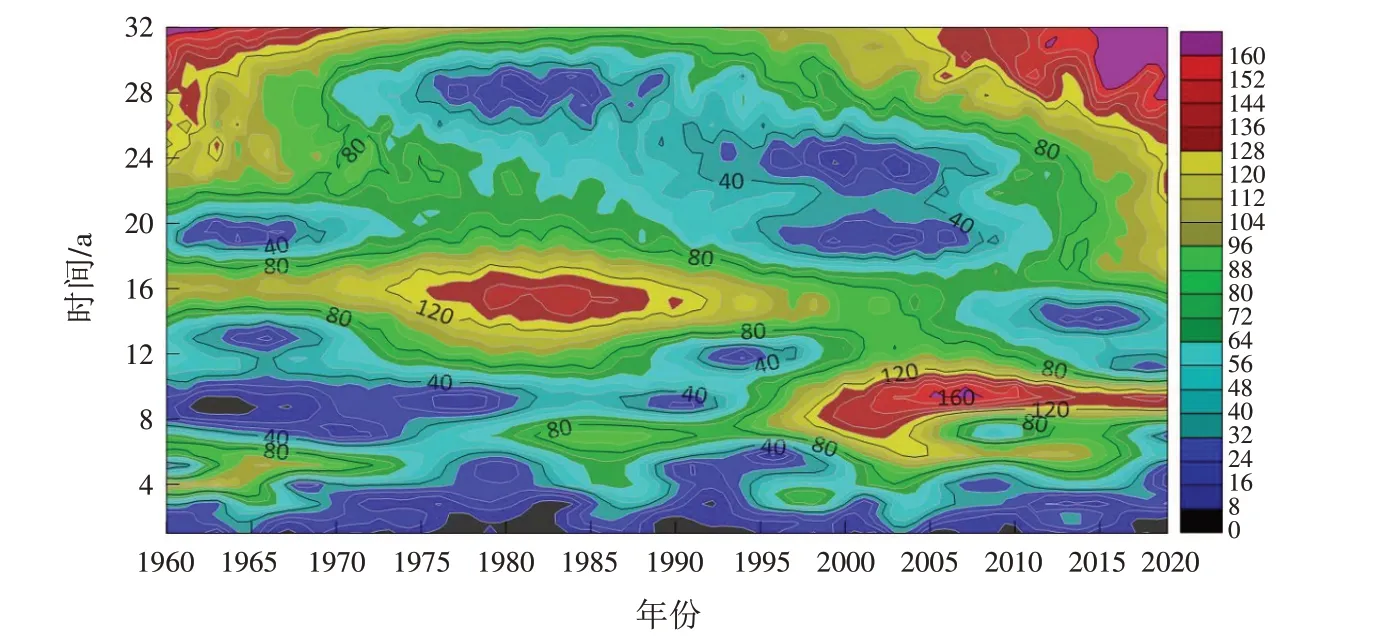
图4 三门峡市降水小波系数的模分布图Fig.4 Modulus distribution of precipitation wavelet coefficients in Sanmenxia City

小波变换系数的模平方分布图（图5）可以显现出来震荡能量的强弱，不同时间尺度上信号的强弱分布不同：9 a和16 a前后时间尺度的震荡能量最强，周期最显著，但周期变化有局部性；9 a时间尺度震荡能量主要表现为2007—2019年；16 a时间尺度的震荡能量主要表现为1990年以前，震荡中心在1983年；6 a时间尺度震荡能量分布与前两个时间尺度相比较弱，但从图5中可以看出其震荡能量分布于整个研究时域.

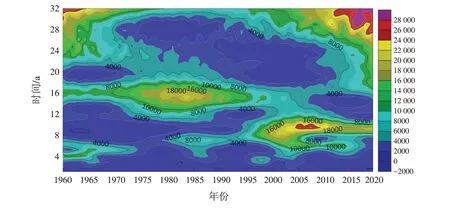
图5 三门峡市降水小波变换系数模平方图Fig.5 Modulus square diagram of wavelet transform coefficients of precipitation in Sanmenxia City

将小波系数代入式（4），得到关于年距平降水量方差，以小波方差Var值为纵坐标，时间尺度a为横坐标绘制三门峡市降水的时间尺度小波方差图（图6）. 从图中可以明显看出，三门峡市年降水序列存在3个尺度周期，即在曲线的峰值6、9、16 a处. 其中16 a为时间尺度中的最高峰值，也表示周期震荡最强，定义为该时间尺度的第一主周期，9 a和6 a分别为第二、第三周期.

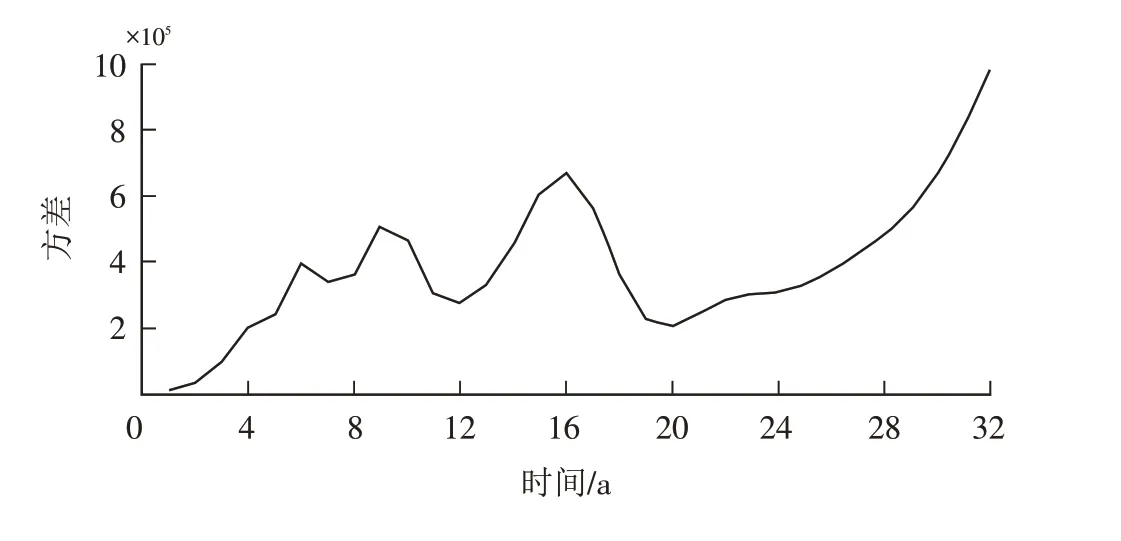
图6 三门峡年降水序列Morlet小波方差分析Fig.6 Morlet wavelet variance analysis of annual precipitation series in Sanmenxia City

2.3 降水量的突变检验

用Mann-Kendall 检验方法将三门峡市降水量数值进行突变检验，显著性水平α=0.05，对应的临界值±1.96，求得Mann-Kendall 统计量曲线图（图7）. 由图7可知，UF和UB有多处交点，分别是1960—1961 年、1963—1964 年、1968—1969 年、1972—1973 年、1990—1991 年、2010—2011 年、2017—2018 年. 但由UF 曲线看出，1961—1973 年、2000—2016年年降水量为下降趋势，1973—2000年、2016—2020 年为上升趋势，可信突变点为1960—1961年、1972—1973年，说明年平均降水量在这两点前后有不同的变化趋势，前者从多变少，后者从少变多. 且根据上升下降变化趋势的周期来看也比较符合小波分析中的16 a第一主周期的分析.

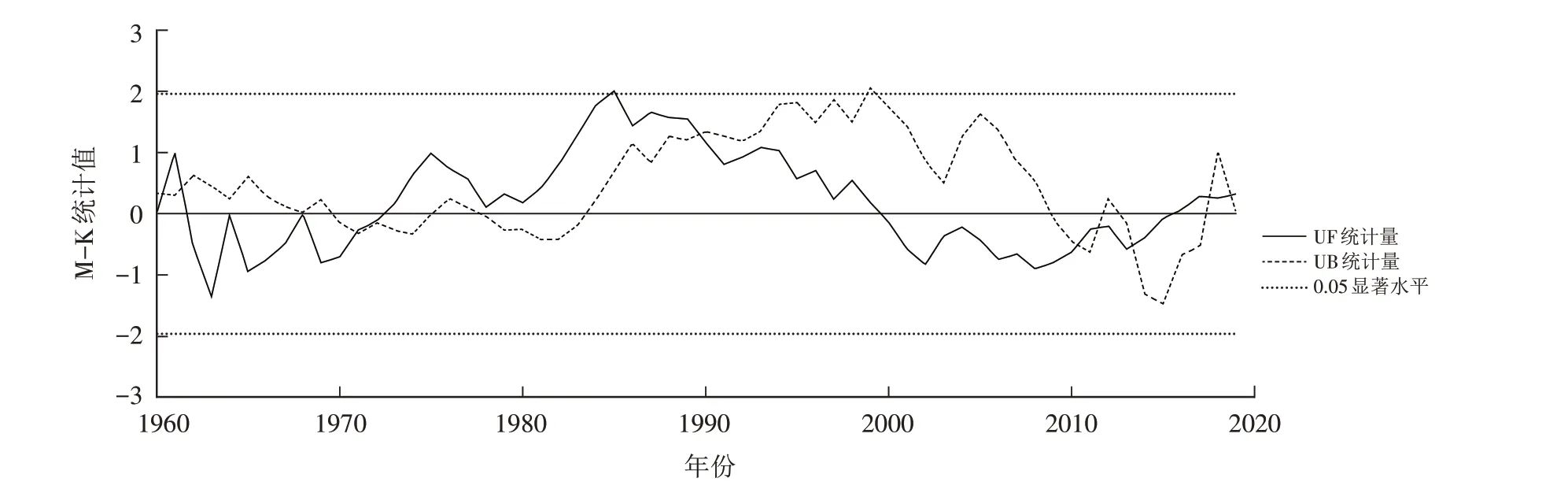
图7 三门峡市年平均降水Mann-Kendall统计量曲线图Fig.7 Mann Kendall statistics curve of annual average precipitation in Sanmenxia City

3 小结

1）从趋势分析来看，三门峡市年降水量的变化曲线呈下降趋势，但不显著，没有通过α=0.05 水平的显著性检验；气候倾向率-0.35 mm/10 a，年降水量332.6～899.4 mm，平均值552.9 mm；研究时段内多雨18 a，少雨20 a.

2）在不同时间序列下，三门峡市降水量的偏多、偏少状况交替出现变化不同，局部化特征较明显；较明显的周期变化规律为12～19 a，其次还存在着20～32 a以及3～7 a两个尺度周期变化.

3）在不同的时间尺度下，三门峡市降水序列存在周期振荡变化，周期振动最强的为16 a左右，还存在着9 a和6 a的周期变化.

4）Mann-Kendall 突变检验结果显示，在1960—1961年突变点前后降水量由上升变为下降趋势，1971—1973年突变点前后降水量由下降变为上升趋势.

5）小波分析图可显示出各种时间尺度周期的强弱和分布，根据小波分析得出的降水偏多或偏少的分布变化趋势和周期性变化规律，可为三门峡市的降水预报以及暴雨旱涝方面的防灾减灾预警提供方向和依据.