新乡市商铺租金的空间结构特征及其影响因素

杨建波， 李 玮， 宋富强

（河南省科学院地理研究所，郑州 450052）

研究商铺出租中租金的空间结构及其影响因素，对加强土地市场的宏观调控、提高土地利用的效率以及优化土地资源配置都具有重要意义.

国外学者于20世纪末开始对商铺租金进行研究，以中心地理论、零售集聚理论、零售需求外部性理论等三种理论为研究基础，主要集中于商铺租金的构成［1］、商铺租金的估算和预测［2-3］、商铺租金的决定因素等方面. 其中，城市之间以研究商铺租金的GDP、商业税率、居民收入［4-5］等宏观经济因素为重点，而城市内部则以区位条件、交通条件、商圈购买力、人流量、经济潜力等微观因素为重点［6-11］. 商铺的租金和地价由于涉及商业机密，因此数据获取难度较大，难以运用相关的数学模型分析方法进行预测，产生的结果也难以有公信力，中西方在发展背景、经济水平、消费习惯等方面存在较大差异，在国外研究中比较常见的影响因素（停车位、建筑年代、主力租户等）对中国商铺租金影响并不一定显著［12］.

目前为止，国内对于商铺租金的研究仅限于北、上、广、深等一线城市，二三线城市的研究较少. 黎林等［13］从地铁和商家需求两个角度入手，运用德尔菲法、层次分析法及市场比较法构建地铁商铺租金定价模型，有效解决地铁商铺租金的定价问题；杨琦峰等［14］建立了影响城市地铁商铺租金的微观特征因素指标体系，运用聚类分析法对有效客流量等因素进行估算，提出城市地铁商铺租金定价优化的定价方法；聂冲和贾生华［15］以长三角和珠三角356 家非主力店作为研究对象，定量分析了购物中心非主力店的租金影响因素；聂冲和贾生华［16］以中国城市购物中心为研究对象，构建和检验了影响购物中心商铺租金的特征价格模型，验证了区位特征对于购物中心租金最重要；张仕康和王梦梦［17］以重庆市沙坪坝商圈餐饮商铺为研究对象，构建了特征价格模型，并对餐饮商铺租金与影响因素之间关系进行定量研究，发现店铺的面积越大租金水平越高；以上研究虽取得了一定进展，但大都属于对商铺租金高低的内部因素的研究，而对于商铺租金的空间结构规律及其外部影响因素的研究较少. 本文以2020年新乡市外业调查获得的商铺租金样点调查数据以及收集的人口密度数据为依据，以新乡市定级范围为研究区域，采用空间自相关、Kriging 插值等方法对交通条件、公共服务设施完备度、人口密度几项外部影响因素进行空间分布研究，以揭示新乡市商铺租金的空间结构及其影响因素.

1 研究区域概况

2020年，新乡市中心城区建成区面积约107 km2，比2010年增长17.6%，城市人口108万人，比2010年增长2.6%，市区人口密度6873 人/km2. 城镇化率为44.69%，比2010 年增长6.15%，增均增长1.23%. 目前，新乡市区内公交线路共78条，主干公交线路平均每3～5 min发一次车，市中心周边一定距离内不到500 m就可以坐上公交车，完全实现了“有路就有公交车”. 新乡市房地产市场已经步入快速发展期. 其中心城区内土地资本的投入显著增加，土地开发强度明显提高，土地供求状况也发生了较大变化，城区内两房改造力度增强，区域内土地空间分布规律及地价水平也发生了较大变化.

2 研究方法及数据来源

2.1 研究方法

空间自相关分析在地理、经济及生态等领域得到了广泛的应用，主要分全局自相关和局部空间相关［18］.全局自相关主要用于分析数据在所研究区域内的空间分布特征，而局部空间相关则主要用于分析每一空间单元与其周边空间单元的关联程度［19］. 目前的Moran指数（Moran’sI）应用最多. 本文主要采用Moran’sI为度量指标，来测验新乡市定级范围内的商铺租金空间分布的集聚性，采用局部自相关（LIST）来研究定级范围内商铺租金的集聚类型［20］.

Moran’sI计算公式如下：

式中：n为空间单元数目；xi为空间单元i的属性值；为n个样点数据的平均值；wij为空间权重系数矩阵.

Moran’sI取值范围是［-1，1］. 若I=1，表示样点数据属性在空间上不相关，即随机分布；若I>0，则表示呈空间正相关，即呈集聚空间格局，且I值越接近1，正相关性就越强，反亦然［21］.

LIST计算公式如下式：

式中：n为空间数据数目；xi为空间单元i的属性值；为样点数据属性的平均值；wij为空间权重系数矩阵.

当LIST>0时，表明空间单元i与邻近空间单元样点数据属性间存在较强的正空间相关性，即呈现局部的空间集聚性.

Moran’sI和LIST两者均要采用标准化进行显著性检验，检验的Z-Score公式如下：

式中：Z-Score代表待测样点的空间自相关的显著水平；E(I)代表待测样点的数学期望；Var(I)代表方差.

当Z-Score值为正数且显著时，表明存在空间正相关关系，当Z-Score的值为负数且显著时，表明存在空间负相关.

2.2 数据来源及处理

商铺租金数据来源于2018年新乡市实际调查值，价格时点为2018年1月1日. 由于不同房源租金之间存在差异，为消除个别因素影响，使结果能更好地反映新乡市商铺租金水平，本文对数据处理如下：①一般情况下，按照商铺店面面积等于临街深度与临街宽度两项之积，然后将不符合条件样点删除. 当商铺为两层或三层时，其租金比一层商铺租金高，但不会超过其2 倍，不符合条件时也删除. ②用离群值减弱离群值对正态分布影响，使调查数据的直方图更接近于正态分布. 本文中所涉及商铺调查样点数据、学校样点及公交站点，均来源于2018 年实际调查值，人口密度数据来源于国家基础地理信息中心2020 年100 m 精度的栅格数据. 借助ArcGIS 软件建立空间数据库，对定级区域内的现状及规划道路进行处理，获得商铺租金空间结构特征及其影响因素的基础分析底图，如图1所示.

图1 租金样点分布图Fig.1 Rent samples distribution map

3 结果与分析

3.1 商铺租金的空间集聚特征

运用ArcGIS进行空间自相关分析、局部自相关分析及Kriging空间插值分析，计算商铺租金空间分布整体相关性，探索租金高低值集聚空间与异质空间的具体位置.

3.1.1 全局空间自相关

依据式（1）计算得到新乡市商铺租金Moran’sI为0.482，其中P<0.01，Z-score=89.24. 表明新乡市商铺租金空间分布在99%水平下，显示出较强全局正相关特征，即租金相似的商铺在空间上集中分布如图2，租金受周边商铺租金水平影响显著，租金形成存在依赖性.

图2 商铺租金空间自相关模式分析Fig.2 Analysis on autocorrelation model of shop rent space

3.1.2 局部空间自相关

对新乡市定级区域内商铺租金点状数据局部自相关性分析，推算聚集区（spatial hot spot）具体空间位置.根据式（2），对其进行局部空间自相关分析，Z值得分为12.62，在99%水平下形成局部空间自相关集聚图（图3）.

图3 局部自相关集聚分布图Fig.3 Local autocorrelation clustering distribution map

由图3显示，商铺租金呈现4种空间关联结果：①高-高（HH）模式，即该商铺租金与周围商铺租金均高于全部商铺租金的平均值，图3中以深红色点为代表. ②低-低（LL）模式，该商铺租金与周围商铺租金均低于全部商铺租金的平均租金，图3 中以深绿色点为代表. ③低-高（LH）模式，表示该商铺租金低于平均租金，而周围商铺租金却高于平均租金，图3中以浅绿色点为代表显示. ④高-低（HL）模式，表示该商铺租金高于平均租金，但其周围商铺租金却低于平均租金，图3中以橙黄色点为代表. 还有一些其他的点则是没有通过显著性检验样点，具有随机性，以浅灰色点为代表. 高-高（HH）和低-低（LL）模式均说明了租金在空间分布具有较强的正相关性，即租金空间集聚分布显著，而“高-低”和“低-高”模式则存在较强空间负相关性，即存在局部异质性.

3.1.3 商铺租金空间结构

用log函数对商铺租金变换，用普通克里金插值对未知租金区域进行处理［21］，分析知，以采取稳定型模型拟合效果最佳，其主要参数为：块金值0.15，偏基台值0.20，主变程2 602.99. 即在定级区域内，通过已知样点租金来预测未知样点的租金，得到新乡市的租金空间结构图（图4）.

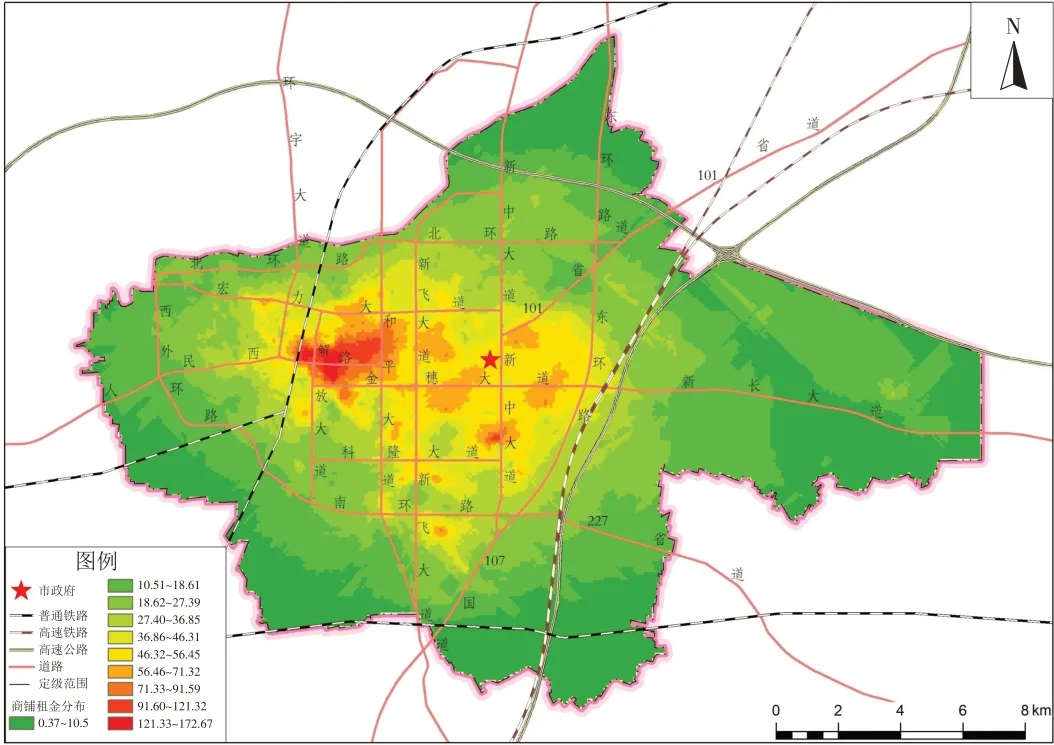
图4 商铺租金空间分布图Fig.4 Shop rent space distribution map

新乡市商铺租金空间结构表现为：①整体上，租金梯度呈同心环分布，租金具有明显向心性，并由市中心向外围递减. ②城市中心西部区租金高于东部区，且西部区租金梯度下降平缓. ③城市中心存在两个高值区，分别位于丰华街与道清路交叉口一带和新乡市人民公园周边. ④租金分布呈放射性延伸，且放射形态与道路方向也大体一致，如科隆大道和丰华街交叉口的南北向，及道清路与丰华街交叉口南，都存在租金高值的外延.

3.2 商铺租金空间分布影响因素分析

依据主导因素原则以及结合新乡市实际，本文选取了商服中心、交通条件、教育服务设施、人口密度4个影响因素，并分析租金与影响因素之间的关系.

3.2.1 商服中心

城市商服中心的繁华程度，不仅对沿街商铺楼面地价有显著提升，其对租赁价格同样适用［22］. 根据全市中心城区收集的商服中心资料，其划分以百货大楼、宝龙城市广场等14个商服中心，分为三个级别，其中一级商服中心1个，二级商服中心6个，三级商服中心8个. 结果表明：商服中心分值较高的主要集中在老城区，且以老城区为中心逐渐向外扩散（图5）.

图5 商服中心作用分值图Fig.5 Commercial service center function score chart

结合图4 和图5 可知，新乡市商铺租金空间分布特征如下：①租金相近的商铺整体上呈现出较为明显的集聚类型分布格局.②商铺租金分布格局的空间偏向差异性显著，即空间分异性显著. 高-高值区租金水平在4320 元/月，主要分布在西部的红旗区政府附近，丰华街道清路一带；高-低值租金有5070 元/月，在定级区域内呈零散分布；低-高值租金在860元/月，其与高-高值集聚类型交错分布；低-低值租金为540元/月，集中分布在城区东部，包括牧野大道周围，纺织路与胜利路交叉口，以和平大道和向阳路为分界，在城区的西北、东南与西南、东北方向上呈现出一定差异性，该交叉口西北与东南租金高值集聚显著，集聚区域占总调查样本数据的31.1%，商铺租金样点分布呈现出小集聚、大分散特点. ③租金价格的高低主要和区位因素中的商服中心远近关系密切，且与道路呈正向性分布，同时也依附公交站点集聚、公共教育用地完善程度. ④高-低值租金商铺空间集聚特征明显，低-低集聚类型集聚分布，高-高与低-高值租金商铺空间集聚类型掺杂集聚分布，而高-低集聚类型则主要呈零星分布.

3.2.2 交通条件

交通工具的便捷性不仅对沿街住房价格有显著提升，该规律也同样体现在沿街商铺租赁价格上［22］. 其提升主要表现为：①公交站点密度分布图有三个高值区，呈圈层结构逐层向外扩散，位于红旗区政府周围高值区覆盖范围最大，且以新乡市人民政府为中心，点位密度分布图高值区向心趋势较强. ②公交站点的圈层分布对主干道路具有凸起效应，其高值区在主干道路上有延伸，这在解放大道人民路交叉口表现最明显，在金穗大道东西方向也有延伸（图6）.

从图4 和图6 可知，公交站密度与租金分布趋势大致相同，其高值覆盖面明显大于租金的高值覆盖面，且公交站密度高值区逐步以政府为中心，呈现向心型分布，这与新乡市发展方向也相契合，总体上实现了市中心由老城区（西）向新市政府（东）的转移，且租金圈层分布情况与公交站点密度吻合度也较高，如在城南庄周围和市教育局南、柳青路北丰华街一带，公交站点密度高值区与租金分布高值区部分重叠；而在饮马口和市烈士陵园周围公交站点密度高值区明显不是租金高值区，差异原因主要是老城区现状道路不规整，道路通行较困难，使老城区租金较低；同时，规整道路网、便捷的交通是形成租金高值的前提，因此在新乡市人民政府周围出现了公交站点密度高值区. 总体上，交通条件优劣能够在一定程度上反映租金水平的高低.

图6 公交点密度分布图Fig.6 Bus point density distribution map

3.2.3 教育服务设施

本研究通过对中学、小学、幼儿园等共同组成的教育用地服务设施的分布情况，来分析商铺租赁需求.由图7可知新乡市教育用地情况：整体上，教育用地密度呈同心圆分布，总体从市中心向周边递减. 东部区密度低于西部区，且东部区密度梯度下降也快. 教育设施有2个高值区：①市政府东侧的太行大道东、新飞大道西、科隆大道北、前进路南的区域. ②京广花园附近，教育用地密度高值区向东北延长.

由图4 和图7 可知，学校与租金都是呈现圈层分布且逐层向外扩散，偏高值区域大致相当. 从图3知，教育中学校点密度偏高值区沿和平大道向南北延伸，而租金偏高值区也在和平大道向南北延伸. 二者延伸程度是有差异的：①学校等设施高值区与租金高值区不完成重叠，学校点密度在胜利路、金穗大道、西华大道、人民路所围成区域为高值区，但租金在上述范围并不属于高值区域，而是偏高值区. ②学校点密度低值区在分布范围较广，这与租金低值区分布趋势不同. 综上，偏高值区教育用地分布情况与商铺租金分布情况大致相同，而在高值区和低值区存在差异，这说明了教育用地的分布能为租金的分布规律提供参考.

图7 教育设施点密度分布图Fig.7 Educational facilities point density distribution map

3.2.4 人口密度

借助国家基础地理信息中心2020 年100 m 精度的栅格数据，分析人口密度情况（图8）. 新乡市人口密集区主要分布于新乡火车站附近、河南师范大学周边区域、新乡医学院周边区域，人口一般区主要分布于新乡市中心城区的建成区，人口松散区主要分布于郊区. 原因如下：①新乡火车站附近，主要是因为交通条件较好，人口较密集；②河南师范大学和新乡医学院人口集聚，是因为区域内学生数量多，导致本区域内人口密集.

由图4 和图8 可知，人口密度新乡火车站附近集中，这与租金高值区域相符，人口密度在河南师范大学和新乡医学院附近集聚，但这个高值区并不与租金的高值区相匹配，反而此处属于租金低值区，这是因为本部分区域人口多主要是因为学生数量多. 在高值区，租金的圈层递减结构与人口密度的减小趋势类似，说明市中心大量人口集聚对邻近商铺高租金提供了强大支撑，而在人口低值区，由于所处区位、公共服务设施以及交通条件等外部条件不同，导致商铺租金与人口密度分布不匹配.

图8 人口密度分布情况Fig.8 Population density distribution map

4 结论与讨论

4.1 结论

1）租金水平在市中心周围呈现高-高集聚分布，在东部及定级边界附近的区域呈现出低-低集聚分布.

2）采用克里金（Kriging）插值方法分析新乡市区商铺租金空间分布是与实际分布呈高度一致性. 即商铺租金总体呈环形由市中心向外围逐层递减，在市中心周围和西南方向存在高值异常区以及郊区存在低值异常区.

3）新乡市商铺租金的空间结构受商服中心、交通条件、公共服务设施、人口密度等影响. 其影响情况各不相同.

4）商铺租金空间分布与公交点密度分布图相似，交通便捷性对租金空间结构影响较大；教育设施、人口密度则主要影响局部区域的租金水平.

4.2 讨论

商铺租金受多因素的影响，其空间结构机制形成复杂. 本研究所涉及的商铺租金影响因素主要基于以下假设：①所研究因素影响了租赁商铺的供给与需求，从而影响商铺租金的均衡，如交通条件. ②影响人们对租金的支付意愿，完善的公共服务设施能给人们带来很大的居住便捷性，人的流量大，使得购买能力加强，促进消费，从而人们愿意为商铺支付高额的租金. 而在郊区，公共服务设施配套不足，租赁的价值自然也会降低.本文仅通过以上假设，在宏观程度分析了区位商服中心、交通条件、人口密度以及教育服务设施等因素对商铺租金影响，但商铺自身的装修状况、临街状况以及楼层的高低等微观因素，也会在一定方面影响租金，这是本研究尚未深入探讨的地方；本文对商铺租金受各因素影响程度的大小，以及区位中商服中心影响分析也没有进行深入研究.