基于相对增益和优先级的化工过程协调优化裕量设计
陈耀明,许锋,罗雄麟
(中国石油大学(北京)信息科学与工程学院自动化系,北京 102249)
引 言
在进行化工过程设计时,为了弥补过程不确定性对化工装置正常运行的不利影响,一般设计人员在过程设计时需要对设计变量增加设计裕量。设计裕量通常会降低装置的经济性能,增加设备投资和操作费用,因此设计裕量应尽可能越小越好。Seider 等[1]提出在设计中给设备尺寸增加裕量(overdesign),以保证装置能够在出现不确定性的条件下安全运行,并且主张协调设计、操作和控制优化,以减少化工过程的设计裕量。Narraway 等[2]、Barton等[3]、Lear等[4]和Perkins[5]提出了经济效益下降量(back-off)的概念,其大小表示过程动态特性对经济效益的影响,此经济效益下降量可以作为评价裕量大小的依据。随后Bahri 等[6]进一步发展了Narraway 的理论,提出了一种分别计算在控制系统开环和闭环条件下计算经济效益动态下降量的方法,将稳态设计方法扩展到动态系统,并加入对模型不确定性的分析。在化工领域尤其是石油深度加工领域,许锋等[7]提出了一种基于一阶灵敏度分析的对装置总体裕量进行评价的方法,以催化裂化装置作为典型对象,进行了完整的裕量分析;之后又利用混合整数动态优化,分析操作裕量、工艺裕量和控制性能之间存在的关系,找到兼顾工艺和控制要求的工艺操作点和控制设计方案[8]。
目前,实际化工过程中的设计裕量一般通过设计经验或经济优化给出。首先,设计人员根据自身的设计经验来决定设计裕量的大小,并确定出在此设计裕量下的操作点,但设计经验无法保证经济性能的优化,且具有很大的盲目性。出于对操作安全性的高度要求,设计经验给出的设计裕量一般偏大。
其次,通过求解最优化问题解决设计裕量和操作点的问题,以最小的经济损失代价抵消过程中不确定参数的影响,理论上可以保证设计结果经济性能的最优。经典最优化算法包括用于非线性规划的序列二次规划法(SQP)[9-10]、用于整数规划问题的动态规划法[11-12]等。这些方法数学理论成熟,但难以对复杂模型进行求解,或求解效果较差,容易陷入局部极值,初值影响取优结果等。随着人工智能的发展,一系列模拟自然生命演化现象的现代启发式算法相继提出,如遗传算法(genetic algorithm)[13-14],粒子群优化算法(particle swarm optimiztion)[15-17],蚁群优化算法(ant colony optimization)[18-20]在内的群智能 优 化 算 法 (swarm intelligence optimization algorithm),此类算法主要是基于种群迭代的全局搜索算法,不依赖于所求问题的梯度信息,较高概率收敛于全局最优解;又如模拟退火(simulated annealing)算法[21-22],基于固体物质的退火过程与一般组合优化问题之间的相似性,是一种依靠Monte Carlo 迭代求解的全局概率型搜索算法。这些现代启发式算法在经典优化方法不能或者难以求解的复杂问题上取得了令人瞩目的成就。
但是求解最优化问题的方法用于裕量设计也不是完美的,主要存在以下问题。
(1)当化工过程规模增大,需要进行全流程工艺设计时,涉及的变量和参数众多,需要求解复杂的大规模非线性优化问题,计算复杂。经典优化算法容易陷入局部极值点,启发式算法计算时间太长,优化算法的内部机理不清楚,设置优化参数时无从下手,有一定概率出现明显错误的优化结果。
(2) 绝大多数过程变量在过程设计时的“参与度”是很低的,有经验的设计人员只需要少数的几个关键过程变量即可确定出设计裕量和操作点。如果求解最优化问题得到一个涉及到大部分变量的“一揽子”优化结果,其中包含了许多“参与度”低的过程变量,并且优化值对于设计变量的调整处于一个十分微小的程度,甚至低于可调整的“最小刻度”,达到了可以忽略不计的程度,那么这种“杂而小”的优化结果是十分有悖于设计人员的设计经验的。
(3)过程约束中并非所有约束都有效,设计人员只需要调整若干设计变量或操作变量就可以使操作点远离约束边界,设计人员根据设计经验只关注几个关键的过程变量。纯粹的经济优化方法只能得到一个大而全、多而杂的数值优化结果,需要调整的过程变量众多,找不到关键设计变量和关键操作变量,并不能给设计人员一种具有“方向感”和“协调感”的有效指导。
本文从灵敏度的角度提供了一种寻找对经济性能影响小并能有效移动操作点的关键过程变量的工具。这是一种不依赖于求解优化问题,但却能简单便捷地给出系统的设计裕量和操作点的方法。其核心思路是给出操作变量和设计变量各自的优先级顺序,这个优先级反映了调整各操作变量和各设计变量使系统操作点返回约束条件以内的优先级。
划分优先级主要用到的数学工具为相对增益阵。相对增益阵(relative gain array,RGA)是Bristol[23]提出的,Grosdidier等[24]进一步给出了RGA 数学性质的相关证明,相对增益是一种双向灵敏度,能够更精确反映出自变量与因变量的相关性。Chang 等[25]将RGA 推广到非方系统中得到非方相对增益阵(nonsquare relative gain array,NRGA),Skogestad 等[26]总结了NRGA 的性质,Xiong 等[27]、He 等[28]和任丽红等[29]在相对增益中引入动态信息,形成了稳态信息与动态信息相结合的动态RGA。
本文将自变量划分为操作变量和设计变量,将因变量划分为经济指标和约束变量。拟应用相对增益的双向灵敏度特性,分析操作变量和设计变量对经济指标和约束变量的敏感程度,根据经济指标和约束变量分别对操作变量和设计变量的相对增益划分优先级,针对过程不确定性的大小按照优先级依次调整各操作变量和设计变量,找到对过程经济性能影响最小并有效移动操作点、远离约束边界的裕量设计方案。
当然本文所给出的这种不需要求解最优化问题的协调优化裕量设计方法,相对于求解最优化问题,自然要承担一定经济性能上的牺牲。本文以串联反应釜为例对该设计方法进行验证,与求解经济最优化问题的裕量设计方法进行对比。
1 灵敏度分析与相对增益阵
1.1 灵敏度分析
理想的过程设计应在满足所有约束条件下达到经济最优,优化设计模型为

式中,F为最优设计的目标函数,包括设备投资费用、过程操作费用等;f表示系统的过程状态方程组;g表示系统的约束方程组;x为状态变量;u为操作变量;d为设计变量;p为不确定参数;c为约束变量;cb为对应的约束限;u与d是优化问题的决策变量。在最优设计点处的系统标称值记作x*,u*,d*,c*,在最优设计时不确定参数维持其标称值p*不变。
对非线性模型式(1)~式(3)在最优设计点附近线性化,得到目标函数对操作变量u、设计变量d的稳态灵敏度[30]为

式中,下角标0表示取最优设计点处的偏导数,下文含义相同。
设计变量d和不确定参数p对约束变量c无动态响应,约束变量c对设计变量d和不确定参数p的稳态灵敏度[30]为

操作变量u对约束变量c存在动态响应,不宜用稳态灵敏度描述。当系统改用微分方程描述时,式(2)转化为
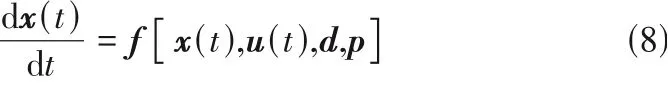
对式(8)在最优设计点附近线性化,得到操作变量u对约束变量c的动态灵敏度为
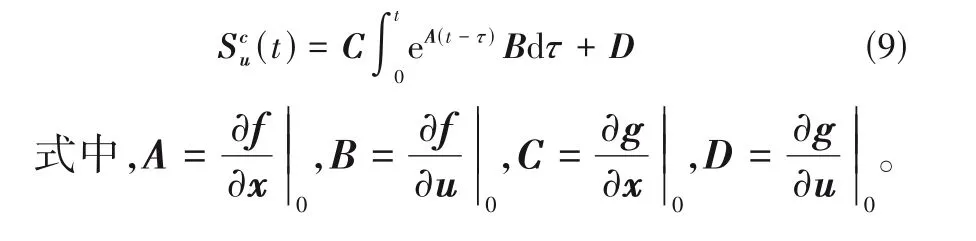
在不确定参数p发生波动时,应确定合适的操作变量的调节方案使约束变量返回约束区间内,并应尽可能对目标函数产生最小的影响。在操作变量u的所有调节方案均无法很好地补偿(即目标函数的性能下降无法令人满意)时,设计变量d应该增加裕量Δd,抵消不确定参数p的影响,保证约束不被突破,在满足系统允许变动的范围内,使目标函数偏离最优值最小。
本文对设计合适的操作变量的调节方案和设计裕量方案,提出以下三点要求。
(1)对经济性能的敏感程度。在基于灵敏度模型设计操作变量的调节方案和设计裕量方案时,此时的调节方案为操作变量和设计变量的线性组合,应尽可能对目标函数(经济指标)产生较低负面影响。
(2)对(突破)约束的敏感程度。如果实际问题中需要使超出约束界限的变量组合尽快返回界限以内,应该根据约束变量距离约束的距离确定需要优先考虑哪些约束变量应当远离约束边界。
(3)操作变量对约束变量的响应速度快慢和设计变量对约束的敏感程度。应当优先选择对约束变量灵敏度高的操作变量和设计变量,使得操作变量和设计变量以较小的变化就能使约束变量远离约束边界。
本文所提出的方法是,在进行操作变量和设计变量的协调优化设计时,首先根据操作变量u和设计变量d对约束变量c和目标函数F(经济指标)的灵敏度来确定u和d的优先级,对每一个约束变量按照优先级依次选择对应的操作变量和设计变量,最后根据操作点对约束变量的要求将约束变量和操作变量/设计变量分别组成方程组,按照先操作变量后设计变量的顺序依次求取操作变量和设计变量,从而确定设计裕量。
1.2 相对增益阵(RGA)
灵敏度仅仅反映了化工过程系统中自变量对因变量的单向敏感信息,而相对增益阵不但包含了自变量对因变量的正向敏感程度,还包含了因变量对自变量的反向敏感程度,同时反映自变量和因变量的双向敏感信息,是一种双向灵敏度。与灵敏度相比,相对增益阵还具有无量纲化和归一化的特点,避免灵敏度因量纲不同无法比对的弊端,能够更加精确反映出自变量与因变量的相关性。
下面给出相对增益阵RGA 的定义及性质。对于自变量U(U∈Rm)和因变量Y(Y∈Rr),其灵敏度关系为

式中,Λ为自变量U对因变量Y的相对增益阵;S为自变量U对因变量Y的灵敏度矩阵;⊗表示矩阵Schur乘积,即矩阵相同位置的元素的乘积。
对于相对增益阵元素λij而言,相对增益为
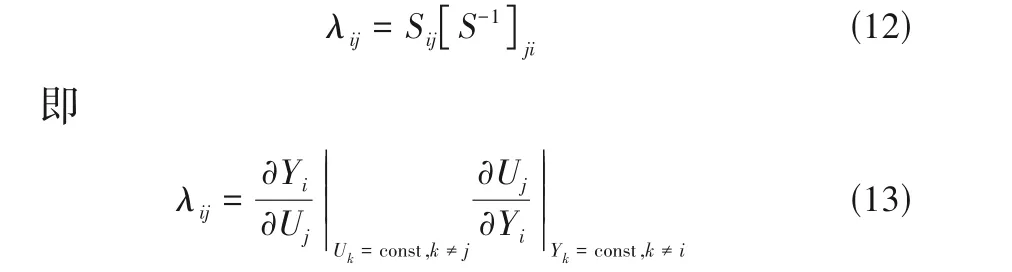
因此,相对增益λij等于自变量Uj对因变量Yi的灵敏度与因变量Yi对自变量Uj的灵敏度的乘积,反映出自变量和因变量的双向灵敏度信息。
相对增益阵RGA 是尺度变换保持不变的,即D1SD2的相对增益阵与S的相对增益阵是相同的,D1,D2均为对角阵。该性质反映出相对增益具有无量纲化的特点,可以避免灵敏度因量纲不同无法比对的弊端。
由于化工过程系统中经济指标和约束变量与操作变量和设计变量的维数一般不相等,对于非方系统,可以用伪逆的概念将相对增益阵推广到非方系统,非方相对增益阵(NRGA)表示为

式中,+表示非方阵的伪逆。
当r>m时,因变量维数大于自变量维数,称为瘦系统,如果S列满秩,则

当r<m时,因变量维数小于自变量维数,称为胖系统,如果S行满秩,则

对于相对增益阵(包括非方相对增益阵)中的元素λij,如果λij= 1,说明自变量Uj对因变量Yi的影响最为显著,自变量Uj只影响因变量Yi,不影响其他因变量,同样,因变量Yi只受自变量Uj影响,不受其他自变量影响。因此,欲对因变量进行调整,应当选择最接近于1 的相对增益对应的自变量进行调节,这样对其他因变量和自变量的影响最小。但是,如果λij= 0,则表明自变量Uj和因变量Yi之间毫无关系,就不能选择自变量Uj对因变量Yi进行调节。
1.3 相对能量增益阵(REGA)
设计变量和操作变量对经济指标的影响,以及设计变量对约束变量的影响,都是稳态关系,可以用灵敏度S表示;但是,操作变量对约束变量的影响具有动态特性,与时间有关,必须用动态灵敏度S(t)来描述,才能与实际过程相符合。
稳态灵敏度S可以求解稳态RGA,但对于动态灵敏度S(t),在计算RGA 时必须考虑动态时域特性的影响,因此,需要在相对增益中引入动态信息,本文采用相对能量增益阵(relative energy gain array,REGA)[29]解决这一问题。
对于动态灵敏度S(t),将动态过程中的灵敏度S(t)和动态过程结束时的稳态灵敏度S(∞)的偏差归一化,得
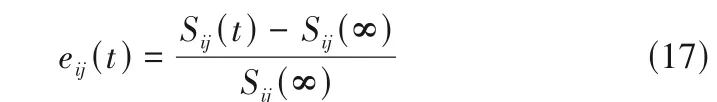
将eij(t)的平方积分定义为自变量Uj对因变量Yi进行调节时的能量消耗,用来表征动态过程的特征,得

综合稳态灵敏度S(∞)和能量消耗Eij,就可以兼顾系统的稳态信息和动态特性。将稳态灵敏度S(∞)和能量消耗Eij组合,得到能量灵敏度Sˉij

将所有自变量对因变量的能量灵敏度Sˉij组合起来,得到能量灵敏度矩阵Sˉ,采用Sˉ计算相对增益阵,对非方系统计算非方相对能量增益阵(nonsquare REGA,NREGA)

NREGA具有与非方相对增益阵相同的性质,需要对因变量Yi进行调整时,应当选择与1 最接近的λij对应的自变量Uj进行调节,这样对整个过程系统的影响最小;同时,不能选择与0最接近的λij对应的自变量Uj进行调节。
2 基于NRGA 和NREGA 的裕量协调优化方法
首先根据存在过程不确定性时约束变量距离约束边界的距离确定约束变量的优先级,确定需要调整其工作点的约束变量;然后根据操作变量和设计变量对约束变量和经济指标的相对增益阵确定操作变量和设计变量的优先级,按照先操作变量后设计变量的顺序依次对约束变量进行调节,保证对过程的经济性能影响最小并有效移动操作点,将其调整到约束边界以内。
2.1 约束变量优先级
由于实际的化工问题常常是瘦系统,约束变量的维数往往大大高于操作变量维数和设计变量维数。各个约束变量距离约束边界的程度确定出约束变量的优先级。如果系统约束变量稳态值已知,结合约束范围,就可以得到系统关于约束变量的优先级向量为
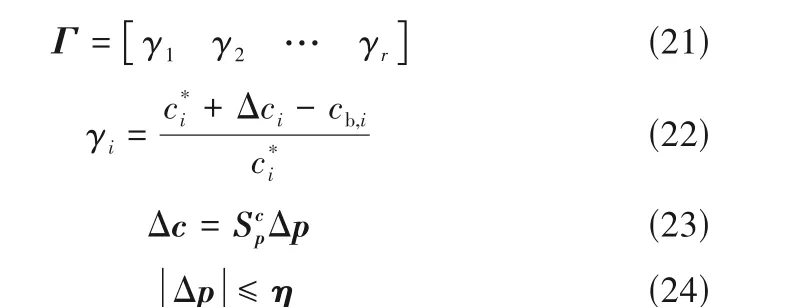
式中,η为不确定参数Δp的变化范围,Δc为在不确定参数Δp影响下约束变量变化量,γi为约束变量在Δp影响下与临近约束边界的距离归一化后的数值。
根据γi从大到小的顺序确定约束变量的优先级,当γi≤0,约束未被破坏,γi数值越大,表明约束变量越接近约束限制;当γi>0,约束被破坏。γi>0对应的约束变量被确定为需要调整的约束变量,需要通过操作变量和设计变量的调节将其调整到约束范围以内。
2.2 操作变量优先级
在确定需要对其调整的约束变量以后,优先采用操作变量对其进行调整。需要调整的约束变量与所有的操作变量组成一个非方系统,按照第1.3节的方法计算操作变量对约束变量的NREGA,记作Λcu。
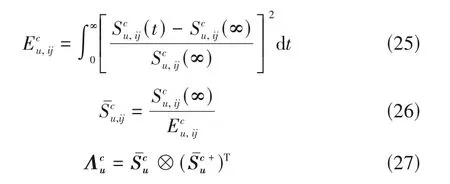
Λcu每行中越接近于1 的元素,在该行所对应的约束变量需要进行调整时,其对应位置的操作变量越优先进行调节。
在操作变量对约束变量进行调整时,应当尽量避免对经济指标产生影响,使经济指标与最优设计的偏差越小越好,对经济指标影响更小的操作变量将获得更高的操作优先级。因此,在确定操作变量优先级时还应该按照第1.2 节的方法计算操作变量对经济指标的NRGA,记作ΛFu。


操作变量对约束变量的调整使约束变量远离约束边界,同时也会使操作点偏离最优设计点,造成经济指标下降。为了让操作变量对约束变量的调节灵敏,同时减少对经济指标的影响,将操作变量对约束变量的NREGA 每行元素减掉操作变量对经济指标的NRGA的对应元素,得到综合REGA

2.3 设计变量优先级
当操作变量到达自身约束上下限,约束变量仍无法被调整到约束边界以内时,需要进一步调节设计变量,才能将约束变量调整到约束边界以内。选取设计变量的优先级排序与选取操作变量的优先级排序是类似的。设计变量对约束变量和经济指标的影响均为稳态模型,可以通过NRGA 确定不同的设计变量对约束变量和经济指标的灵敏度关系。

在设计变量进行调节时,同样会对约束变量和经济指标同时产生影响,增大设计裕量,能够使约束变量返回约束边界内,同时也会增大设备投资和操作费用,造成经济指标下降。理想的设计变量应该对经济指标不敏感,而对约束变量有足够的灵敏度,因此,将设计变量对约束变量的NRGA每行减掉设计变量对经济指标的NRGA向量,得到综合RGA

2.4 操作变量与设计变量的协调优化
在不确定参数发生波动引起约束变量超出约束边界时,应确定合适的操作变量的调节方案或者增加设计裕量使约束变量返回约束区间内,并应尽可能对经济指标产生最小的影响,保证增加裕量后的设计方案与不确定参数未发生波动的最优设计方案偏离最小。
首先,根据第2.1 节确定约束变量优先级,根据约束优先级向量Γ将约束变量排序,依次选择γi>0 的约束变量组成违反约束的约束变量集合ce,违反约束的约束变量需要通过操作变量调整到约束范围以内,其调整量为Δce=[Δce,i]。
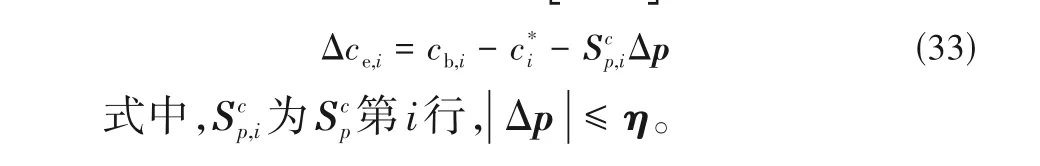
对于约束变量的调整量集合Δce,首先应动用操作变量对其进行调整,根据第2.2 节计算操作变量对约束变量和经济指标的综合REGA,违反约束的约束变量选择相应的操作变量组成需要调节的操作变量集合ue。但是操作变量的变化范围也是受到限制的,当操作变量的调节量到达其上下限后就不能再发生变化,操作变量调节量计算如下

当操作变量到达其上下限,约束变量仍然违反约束,此时约束变量的值为

对此时的约束变量c′根据第2.1 节计算约束优先级向量Γ,依次选择γi>0 的约束变量组成违反约束的约束变量集合c′e,c′e的调整量为Δc′e=[Δc′e,i]。

对于Δc′e,需要对设计变量增加裕量继续对约束变量进行调整,直到约束变量返回到约束范围以内。根据第2.3 节计算设计变量对约束变量和经济指标的综合RGA,对违反约束的约束变量选择相应的设计变量组成需要增加裕量的设计变量集合de,设计变量需要增加的裕量计算如下
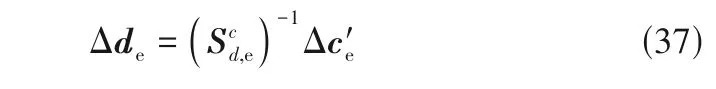
通过以上步骤,针对不确定性对约束的影响,选择对经济指标影响小、被破坏的约束影响大的操作变量和设计变量,对操作变量进行合理调节,对设计变量增加裕量,不需要进行优化,也可以获得合理的化工过程设计。以上步骤可以归结为流程图如图1所示。
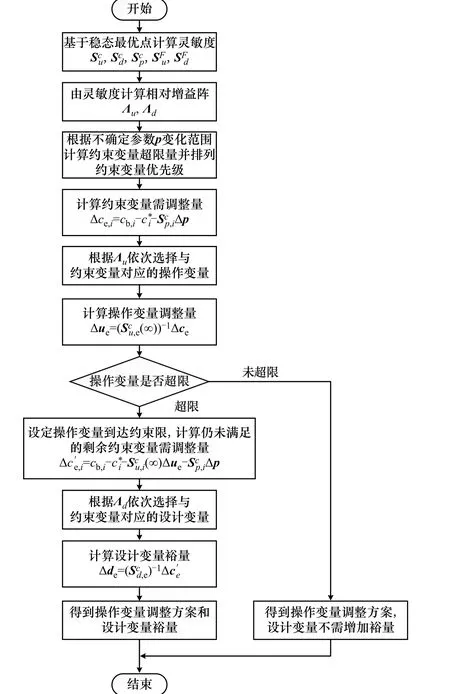
图1 化工过程协调优化裕量设计流程Fig.1 Flow chart of the coordinated optimal margin design method
3 实例分析
以串联反应釜为例对本文基于相对增益和优先级的协调优化裕量设计方法进行了验证,并与求解经济最优化问题的裕量设计方法进行了对比。
串联连续反应釜由两个液相全返混床反应器(continuous stirred tank reactor, CSTR)和一个中间混合槽构成,如图2 所示。液相物料1 进入反应釜1,而液相物料2 进入一个混合槽与反应釜1 的出料混合进入反应釜2。液相物料在搅拌器的搅拌作用下发生一阶不可逆放热反应。由于该反应为放热反应,因此需要在反应釜设置循环冷却水取走热量,保证反应器的热稳定性。

图2 串联CSTR工艺流程Fig.2 Process flow diagram of 2 CSTR in series
在建模时需要作如下简化假定:
(1) 混合物的密度是恒定的,与温度和浓度无关;
(2)液相物料的比热容也是常数,与其温度和组成无关;
(3)两个CSTR 的液体体积不是恒定的,与入口流量有关。
根据化工生产方面的知识,通过物料衡算和热量衡算,引入反应速率方程,通过机理分析建立串联液相连续反应釡的动态数学模型。
反应速率按照一阶反应建模,得

系统的输出变量为两个CSTR 的物料浓度Ci=1,2,温度Ti=1,2和液体体积Vi=1,2。操作变量为第一个CSTR 的进料流量Qf1,中间混合罐的进料流量Qf2,以及两个CSTR 的冷却剂流量Qcw1和Qcw2。设计变量为两个CSTR反应器体积Vd1和Vd2。
过程系统需要满足的约束如下:
(1)为了避免失控和生成不希望的副产品,限制两个反应器的温度

以上约束转化为约束变量c和约束边界cb的形式

式中,F为经济效益[31]。
利用gPROMS 软件求解该最优化问题,得到最优经济效益F为1390。设计变量最优值为

根据γi>0选定c2和c5为需要调整的约束变量,约束变量的调整量为
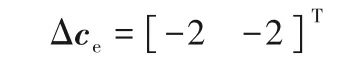
应确定合适的操作变量的调节方案Δu或增加设计裕量Δd使约束不被破坏。期望Δc2、Δc5向负方向移动距离应至少为2,以抵消不确定参数p的不利影响。优先调节操作变量u来达到上述目的,当u到达其上限或下限时,则应预先增加设计裕量Δd来补齐,最终使约束变量回到约束范围以内。
操作变量对经济指标的NRGA为

结合调节灵敏度和经济指标的操作变量综合NREGA为

很明显如此操作,Qf1和Qf2超出了约束限制,得到的Δue是不符合要求的,实际可以投入的Δue应卡住操作变量的约束下限,即
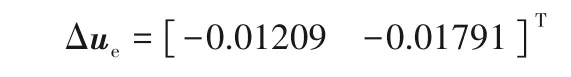
操作变量调节到达约束边界后,约束变量c2和c5的值为1.469 和1.239,仍大于0,超出约束范围。此时已经没有合适的操作变量来调节系统约束变量到达约束以内,所以需要增加设计裕量Δd进一步调节约束变量。约束变量c2和c5的调整量为

结合调节灵敏度和经济指标的设计变量综合NRGA为

最终通过施加操作变量的调节方案和增加设计裕量,系统到达了新的稳态设计点,该设计点可以抗衡不确定参数变化的影响。在新的稳态设计点,其经济性能有所损失,系统的经济指标F为1215。但是这样的设计却保证了约束变量在约束范围以内,可以克服进料量波动的影响,保证装置安全运行。
如果利用gPROMS 软件求解最优化问题,所确立的最优化问题包含29 个模型方程,6 个优化变量(其中4个操作变量,2个设计变量)。考虑进料量波动的条件下,通过调节操作变量和增加设计裕量满足过程约束,经济指标F为1239。最优化方法和本文方法的求解结果及性能的对比如表1所示。

表1 求解方法性能及结果对比Table 1 Comparison of algorithm performance and results between two methods
本文提出的方法不需要求解优化问题,所需消耗的计算机时间忽略不计,与最优化结果相比经济指标仅下降了1.96%,其他数值结果也基本接近,因此本文提出的基于相对增益和优先级的协调优化裕量设计方法直观明了,操作性更好。本实例中的串联CSTR 模型规模仅为29 个方程和6 个优化变量,采用gPROMS 软件求解最优化问题所需求解时间为4.0 s。现实化工过程的规模要比串联CSTR 系统规模大得多,对于大型化工过程求解最优化问题,其时间成本将非常庞大,本文所提出方法则更为轻量便捷。
4 结 论
本文提出了一种不需要求解最优化问题的协调优化裕量设计方法,该方法以一定的经济性能牺牲为代价,以NRGA 和NREGA 作为主要数学工具,描述化工过程设计的自变量和因变量的灵敏度关系。根据经济指标和约束变量的相对增益对操作变量和设计变量划分优先级,按照优先级依次调整各操作变量和设计变量,可以协调地给定合适的操作点方案和设计裕量。本文以串联反应釜为例论证了该设计方法的可行性和便捷性,相对于求解最优化问题的方法,直观明了,操作性好,计算简单,无须求解最优化问题,经济性能也牺牲不大。
最后,需要指出本文所提方法也存在一定的局限性。本文所计算出的灵敏度都是基于稳态最优点处的系统标称值而生成的。灵敏度模型本质上是线性的,因此当不确定参数p变化范围过大,导致系统偏离标称工作点过大时,求出的灵敏度模型就会存在过大的误差,计算出的Δu和Δd将不够准确。在这种情况下,可考虑采用“分片线性化”的方法。首先限定p的变化量,将约束变量需调整量减至一个较小的程度,计算相应的操作变量调整量和设计变量裕量,将其应用到设计对象上,重新确立一个新的稳态点;然后逐步增加p的变化量,更新约束变量需调整量,计算增加的操作变量调整量和设计变量裕量,重复此过程,逐渐得到符合p的变化范围要求的设计结果。此改进方法实质上是用多个分段线性化模型对非线性模型进行拟合,用拟合后的分段线性化模型进行本文的化工过程协调优化裕量设计。
符 号 说 明
A——传热面积,m2
C——反应釜原料A的浓度,mol·m-3
Cf——进料中原料A的浓度,mol·m-3
Cm——混合槽原料A的浓度,mol·m-3
cp——反应物比定压热容,J·kg-1·K-1
cpc——冷却水比定压热容,J·m-3·K-1
E——化学反应活化能,J·mol-1
F——经济效益
ΔH——反应热,J·mol-1
K——反应速率,mol·s-1
k——反应釜出口阀门常数,m3/2·s-1
k0——Arrhenius关系式指前因子,s-1
Q——反应釜出口流量,m3·s-1
Qcw——冷却水流量,m3·s-1
Qf——入口流量,m3·s-1
Qm——混合槽出口流量,m3·s-1
qcool——单位时间冷却水吸收的热量,J·s-1
R——理想气体常数,J·mol-1·K-1
T——反应釜物料温度,K
Tc——冷却水温度,K
Tf——进料温度,K
Tm——混合槽物料温度,K
U——总传热系数,J·m-2·K-1·s-1
V——反应釜物料体积,m3
ρ——反应物密度,kg·m-3
ρc——冷却水密度,kg·m-3
下角标
in——冷却水进料
out——冷却水出料
1——第1个CSTR
2——第2个CSTR
——与非适应性回归分析的比较

