基于最优传质系数的槽型结构参数对液膜机械密封汽化特性影响及优化

许晓东，马晨波，孙见君，张玉言，於秋萍

（南京林业大学机械电子工程学院，江苏 南京 210037）

引 言

液膜机械密封作为非接触式机械密封的典型型式，可借助动压效应增大液膜开启力，形成端面间全流体润滑状态，有效降低端面磨损。在工业生产中端面液膜汽化现象越来越普遍[1]。目前易挥发或易汽化的液体介质在流体工业领域的应用越来越多，当泵在运行时，机械密封端面温升将会导致端面间液膜发生汽化，使得端面流体膜处于汽液混相状态[2-3]。

由于流体膜处于两相状态时，相较于全液膜密封其稳定性较差，所以液膜相变问题成为影响密封工作稳定性和可靠性，甚至导致密封失效的直接因素之一[4]。已有研究表明，虽然相变在一定条件下可以提高液膜承载能力、控制泄漏[5]、降低端面摩擦扭矩，但是超过一定条件之后则会导致不利影响[6-8]，如汽化会导致端面液膜完整性受到破坏，使得分离的动静环端面出现接触情况，造成密封端面磨损、汽蚀损伤、端面热裂等密封失效。

目前，国内外不少专家学者对液膜机械密封相变问题展开了相关研究。Hughes 等[9]、Gu[10]发现可以通过监测端面温度及压力曲线进行相变界面位置的预测。顾永泉[11-12]根据相变界面位置将汽液两相流分为似液相混相及似汽相混相密封，并提出以最大汽相体积分数及膜压系数来进行结构合理性判断。甘延标[13]、Safari 等[14]、吕知盛[15]基于格子玻尔兹曼方法提出不同类别的Thermal LB模型用于解决汽化相变问题。陈汇龙等[16-18]基于黏温效应、饱和温度随压力变化方程和流体内摩擦效应建立汽化相变计算模型，分析讨论了螺旋槽液膜密封相变机理，研究了工况参数对液膜汽化特性及密封性能参数的影响规律。曹恒超等[19-21]、Wang 等[22-23]建立了螺旋槽等液膜相变模型，计算得到了密封间隙内流场与端面压力分布，分析了工况参数及结构参数对液膜相变的影响，研究了相变区域对密封性能的影响。陈银等[24]、冯瑞鹏[25]、张国渊等[26]利用仿真分析软件，结合实验分析，基于不同工况条件下密封性能变化提出结构参数优化设计。马润梅等[27]针对汽化对密封稳定性影响，设计了5 因素5 水平的正交优化实验方案，为密封结构优化设计提供理论基础。陈汇龙等[28]通过响应面法及均匀试验法研究分析了端面型槽结构参数对开启力、泄漏量的影响规律。

在采用计算流体动力学（CFD）方法模拟冷凝或沸腾过程时，存在Lee 模型[29]及Thermal LB 模型，因为Lee 模型具有形式简单、易于计算、可靠性高等优点而被广泛使用。然而，在相关研究中，Lee 模型中的传质方程存在一个传质系数，其中基于Fluent 软件进行汽化仿真分析研究取默认系数[19-21,30]。邱国栋等[31]提出在CFD 模拟汽化相变时，传质系数可以选取较大值，并且取值越大，计算精度越高。

为此，本文以螺旋槽上游泵送机械密封为几何模型，建立基于黏温方程、流体内摩擦、饱和温度与压力关系方程的液膜汽化计算模型，通过CFD 方法分析计算不同传质系数对液膜相变的影响，研究在最优的传质系数条件下槽型结构参数的变化对平均汽相体积分数的影响，并通过均匀试验设计法和响应面法，分析结构参数之间的交互作用对平均汽相体积分数的影响，并对结构参数进行优化分析，为相变条件下螺旋槽机械密封的端面设计提供理论基础。

1 模型建立

图1为动环模型，Ro、Ri和Rg分别表示动环端面的外半径、内半径以及槽根圆半径，θ1和θ2分别表示螺旋槽槽区及堰区对应圆心的角度，θ表示螺旋角，为螺旋线上任意一点的切线与其所在圆的切线的夹角。为了便于分析，做如下定义：槽径比β=(Rg-Ri) /(Ro-Ri)，槽堰比γ=θ1/(θ1+θ1)。

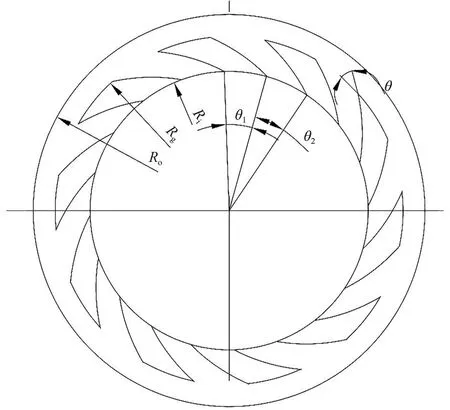
图1 动环模型Fig.1 Dynamic ring model

螺旋槽液膜密封的相变机理非常复杂，为简便计算，做如下简化假设[32]：

（1）流体介质属于牛顿流体；

（2）密封界面间的流体流动为连续介质层流流动，流体温度和黏度不随时间变化；

（3）密封面光滑，忽略其粗糙度对流体流动的影响；

（4）膜厚很薄，在厚度方向上压力和密度保持不变；

（5）密封环的温度及其材料的力学性能不随时间变化；

（6）流体介质与密封端面之间无相对滑移；（7）忽略工作过程中系统的扰动及振动影响。

Lee[29]针对液相和汽相分别建立了独立的守恒方程，其中传质方程蒸发项和冷凝项分别如式(1)和式(2)所示：

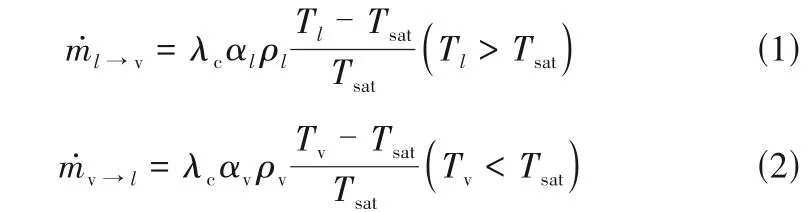
式中，Tsat为饱和温度，K；λc为相变传质系数，可通过实验获得；αl和αv分别表示液相与汽相的体积分数；ρl和ρv分别表示液相与汽相的密度，kg/m3。

ANSYS FLUENT 理论手册[33]中给出了细泡状流下界面浓度计算公式，可以计算得到每一个单元内汽相体积分数，其过程如式(3)：

式中，Ai为界面面积，m2；Vcell为单元格体积，m3。

沸腾及冷凝过程相变传质系数λc可以用式(4)和式(5)来表达[33]：

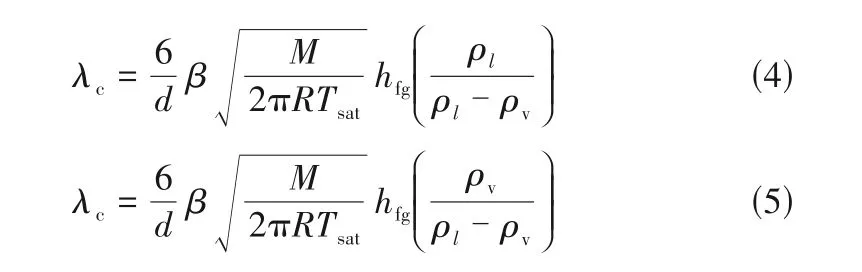
式中，d为汽泡直径，m；β为调节系数；M为摩尔质量，kg/mol；R为通用气体常数，8.314 kJ/（mol·K）；hfg为汽化潜热，J/kg。

液膜出现相变之后，整个流体膜转变为液体与汽体的均匀混合物，根据Wallis[34]对混合物的密度与黏度关系研究，式(6)可以准确解释两者间的联系。

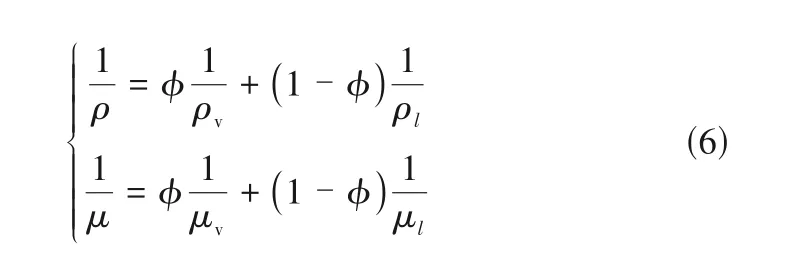
式中，μv和μl分别为汽相和液相动力黏度，Pa·s；φ为混合相中的汽相质量分数。

温度不仅对液膜相变程度存在影响，还对液膜中液相的黏度及密封介质的饱和蒸汽压力存在影响。汽相的黏度远小于液相的黏度，并且受温度的影响较小，基本可以忽略不计。本文中密封介质为液态水，汽相黏度取对应温度下水蒸气的黏度，而液态水的黏度与温度之间的关系方程以及水的饱和蒸汽压与温度之间的关系方程由李新稳[35]的研究可得。

2 求解设置

2.1 计算域几何模型

由图1 可知，螺旋槽在动环端面上沿周向呈现周期性分布，可以认为各槽区及堰区的流场运动状态相同。为了提高计算效率并降低计算成本，取其中一个槽区作为计算域，如图2所示，其中图2（b）为液膜厚度放大200 倍的计算流体域。通过Fluent 软件中用户自定义函数，将饱和温度曲线方程及黏温方程编译并加载进Fluent软件中。

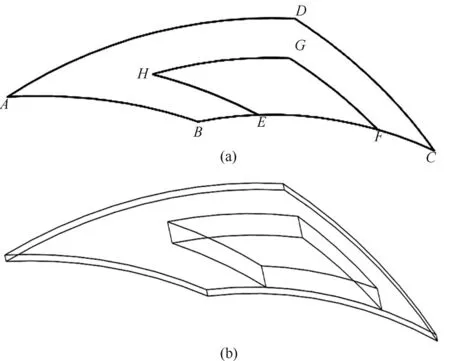
图2 计算域几何模型Fig.2 Computational domain geometry model

2.2 网格划分

运用六面体结构网格划分计算域。由于模型的槽深及膜厚为微米级，与模型其他尺寸参数相差数个量级，为达到计算精度要求，首先利用分块功能将计算域分为螺旋槽区及液膜区，再通过对各区域边界进行节点数定义以保证整体网格质量达到良好的计算精度[36]。

为了在满足计算精度的同时降低计算成本，对网格数为79749、146397、257420、367819、577060 个时平均汽相体积分数进行了比较分析。在网格数为367819个时相对误差为1.5%，平均汽相体积分数受网格的影响已经很小。同时考虑到网格数量对计算成本的影响，决定以该网格数量为标准进行网格划分。

2.3 边界条件及求解器设置

基于有限体积法对控制方程进行离散，选择双精度、压力基求解器。多项流模型选择Mixture 模型，相变模型选择evaporation-condensation 模型，mass transfer coefficient 选择0.1、2、4、6、48，算法选择SIMPLEC 算法，压力离散项选择PRESTO！格式，动量及能量项选择二阶迎风格式，体积分数项选择一阶迎风格式，压力松弛因子设为0.3，收敛精度设置为10-6。

计算域边界条件设置如表1所示。

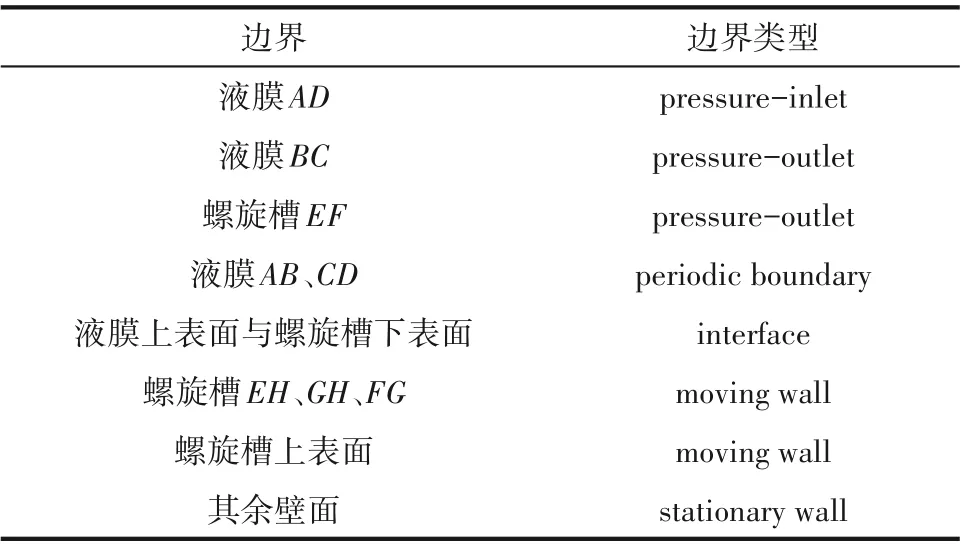
表1 边界条件设置Table 1 Boundary condition setting

2.4 模型验证与最优传质系数确定

为了验证模型的合理性，将仿真模拟计算结果与曹恒超等[20]（采用默认传质系数0.1）所得结果进行对比，如图3 所示。由图3 中可以看出本文使用默认传质系数（0.1）计算出的平均汽相体积分数数值与文献中结果基本一致，验证了仿真计算结果的正确性。但从图中还可以看出，随着传质系数的提高，平均汽相体积分数逐渐增大且变化较为明显。图4 所示为平均汽相体积分数随传质系数变化曲线，从图中可以看出，随着传质系数的增大，平均汽相体积分数急剧增大，但当到达一定数值后趋于稳定。当传质系数设为48之后，每次计算得到的平均汽相体积分数相较于前一次计算结果，增长率已经低于1%，考虑到计算效率以及成本问题，本文选用48作为优化的传质系数进行仿真计算。

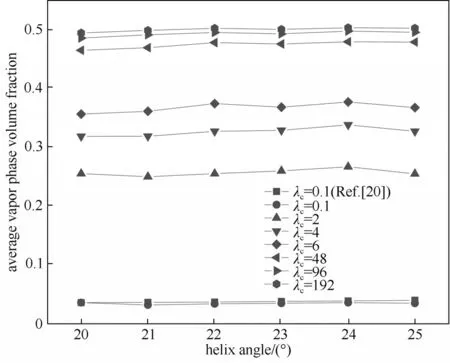
图3 不同传质系数条件下平均气相体积分数随螺旋角的变化Fig.3 Variation of average gas volume fraction with helix angle under different mass transfer coefficients

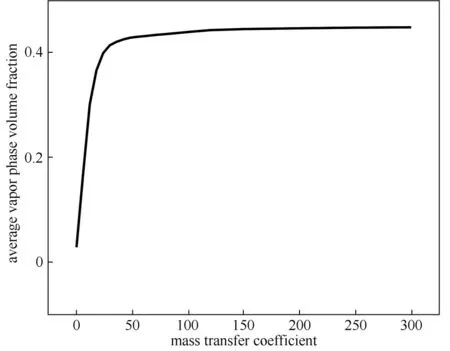
图4 平均汽相体积分数随传质系数变化曲线Fig.4 The average vapor phase volume fraction varies with the mass transfer coefficient

3 结构参数影响分析

为了便于讨论螺旋槽液膜密封型槽结构参数对平均汽相体积分数的影响，考虑到工况参数的改变会对以上密封性能参数造成影响，取压力入口Pi= 1 MPa、入口温度Ti= 393 K、出口压力Po为标准大气压、出口温度To= 300 K（环境温度）、转速n= 3000 r/min、槽数为12 个、端面外径Ro=31 mm、端面内径Ri=26 mm 作为固定参数。其余参数变化范围如表2所示。

表2 槽型结构参数变化范围Table 2 Variation range of trough structure parameters

3.1 均匀实验设计

根据表2，系统设计4 因素、17 水平的均匀设计表U17(174)[37]，带入设计变量参数后，根据每一组参数分别建立计算域几何模型，运用CFD 方法进行数值模拟。相应的因素可以参数化设计为：

(1)螺旋角θ，记为x1；

(2)槽径比β，记为x2；

(3)槽堰比γ，记为x3；

(4)槽深hg，记为x4。

由于上游泵送螺旋槽机械密封各结构参数之间存在交互影响，根据均匀实验结果可以列出描述多个实验因素（x1,x2, …,xm）与响应值（y）之间的二次多项式方程。本文所求的二次多项式回归方程的格式为：

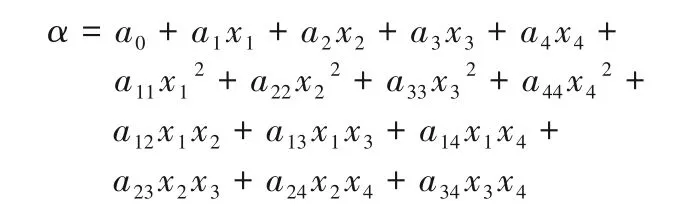
具体结构参数及计算结果如表3所示。

3.2 响应面法分析

将表3 中数据使用响应面法分析。图5 所示为螺旋角、槽径比、槽堰比、槽深两两相互作用响应面曲线及等高线图。从图中可以看出，在给定范围内，槽径比对平均汽相体积分数影响最大，其次分别为槽堰比、螺旋角，此外，螺旋槽槽深对平均汽相体积分数的影响最小。

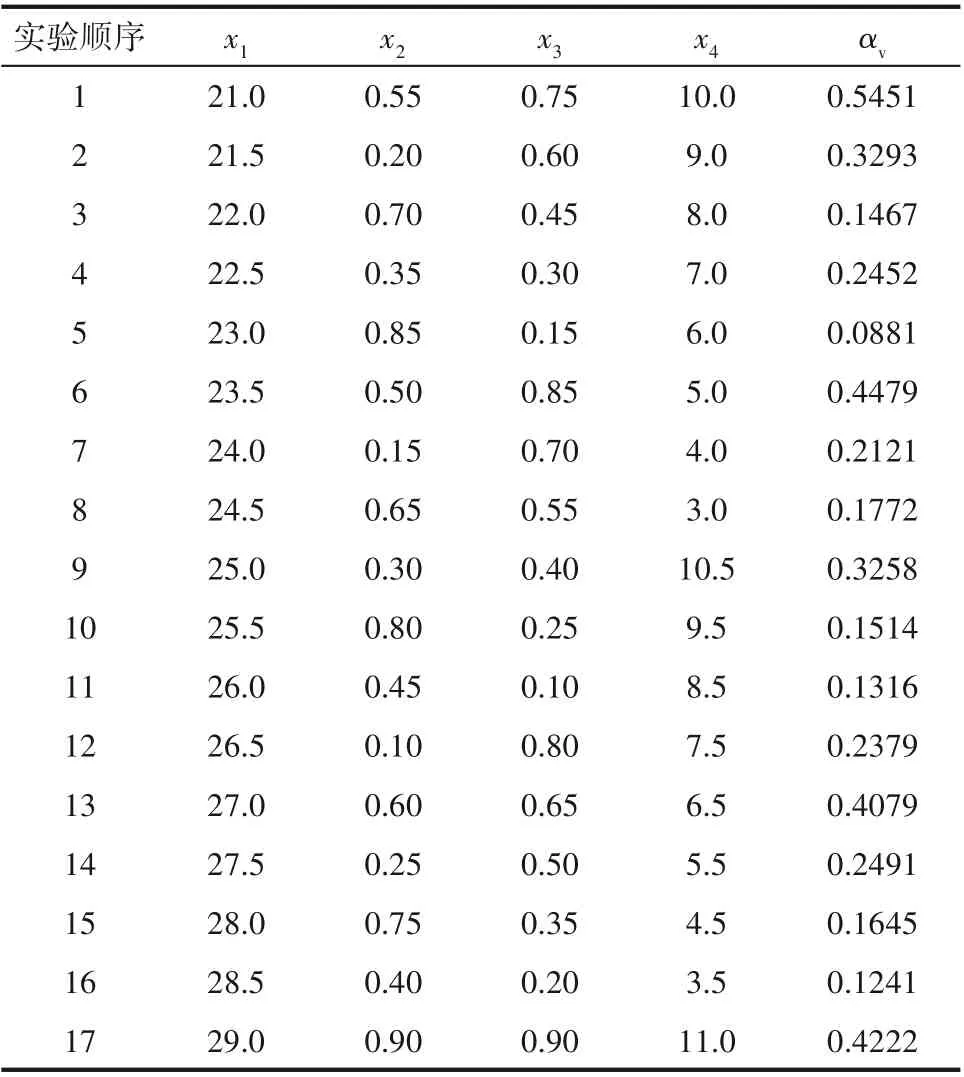
表3 均匀实验表Table 3 Uniform experiment table

3.2.1 单因素分析 由图5（a）～（c）可知，在螺旋槽θ处于20°到30°的范围内，平均汽相体积分数随着螺旋角θ的增大而不断增大。螺旋角θ的增大，导致螺旋槽背风侧工作面面积减小，同一时间内压力突变增加，使得槽区范围内压力逐渐减小，且低压区域逐渐增大，使得汽化相变区域不断增大，从而导致平均汽相体积分数增大。

由图5（a）、（d）、（e）可知，平均汽相体积分数随着槽径比的增加先增加后减小，在槽径比为0.5 时取得最大值。当槽径比较小时，螺旋槽背风侧工作面面积较少，压力突变区域较小，低压区在整个液膜中不够明显，相变程度较低，平均汽相体积分数较低。随着槽径比逐渐增长，螺旋槽背风侧工作面面积不断增加，低压区域范围越来越大，相变程度不断提高。然而，螺旋槽迎风侧工作面的面积也在不断增加，使得动压效果越发明显，在槽径比为0.5时，螺旋槽区域的动压效应对相变的抑制作用超过了低压区相变的产生，从而有效抑制了相变的发生，导致平均汽相体积分数显著降低。

由图5（b）、（d）、（f）可以看出平均汽相体积分数随着槽堰比的增加而增加。在槽堰比为0.1 时，两个周期螺旋槽之间存在较大的堰区，槽区较小，液膜流动时形成的低压区也较小，相变区域较小，造成平均汽相体积分数较小。随着槽堰比的增加，堰区在两个周期内所占的区域逐渐减小，而槽区逐渐增大，液膜低压区域不断增加，相变区域也不断增加，平均汽相体积分数随之增加。当槽堰比为0.9时，两个周期螺旋槽之间的堰区最小，槽区最大，形成的低压区域也达到最大，相变程度最高，平均汽相体积分数增大到最大。

图5 交互作用响应曲面图Fig.5 Interaction response surface plot

由图5（c）、（e）、（f）可以发现，随着槽深的增加，平均汽相体积分数不断增加。随着螺旋槽槽深的增加，螺旋槽背风侧高度差不断增加，使得液膜压力突变程度不断增加，低压区域逐渐扩散，相变程度逐渐增加，造成平均汽相体积分数逐渐增加。

3.2.2 交互影响分析 综合分析图5（a）～（c），从图5（a）中可以发现，槽径比对平均汽相体积分数的影响在数值为0.5 处呈对称分布的现象，并且随着螺旋角的增大，其变化幅度越发显著，并在槽径比为0.45～0.55 之间存在平均汽相体积分数极大值；图5（b）中体现了当螺旋角不变时，槽堰比的增加使得平均汽相体积分数增加，并且槽堰比越大，增长幅度越小。同样，随着螺旋角的增大，槽堰比的增大对平均汽相体积分数的影响逐渐减小；图5（c）中可见螺旋角不变时，螺旋槽槽深的增加，使得平均汽相体积分数增加，当螺旋角增大时，螺旋槽槽深越深，平均汽相体积分数变化越显著。

图5（d）～（e）分别表示槽径比与槽堰比和螺旋槽槽深之间的交互关系。从图中可以看出槽径比与槽堰比的交互影响远比槽径比与螺旋槽槽深的交互影响要显著。图5（d）中显示的平均汽相体积分数分布规律与图5（a）中显示的结果一致，在槽径比的变化范围内呈对称分布趋势，并且都存在一个极大值。同样，在槽径比不变的条件下，槽堰比及螺旋槽槽深的增加，都会导致平均汽相体积分数增加。

图5（f）表示的是槽堰比和螺旋槽槽深两个因素对平均汽相体积分数的响应曲面关系，其交互影响显著。可以发现，螺旋槽槽深一致时，平均汽相体积分数随槽堰比的增大而增大，并随着槽堰比的增加，螺旋槽槽深的增加导致平均汽相体积分数增长幅度越发显著。

4 结构优化

非接触式机械密封常见的失效形式有：端面磨损、汽蚀损伤、端面热裂以及端面剥落等。引起这些失效的原因之一是液膜相变，当液膜发生汽化时，液膜的稳定性遭到破坏，两端面出现接触可能，以及汽化产生的气泡的生成及溃灭会对端面造成冲击，从而导致非接触机械密封端面密封失效。所以螺旋槽机械密封在运行时，相变程度需要进行一定的限制，降低密封端面失效的可能性。

4.1 优化模型

本文研究发现，端面型槽结构参数的改变对平均汽相体积分数的影响较为显著，所以为了控制汽化程度，满足密封稳定运行要求，以平均汽相体积分数为优化目标，以螺旋槽的螺旋角、槽径比、槽堰比以及螺旋槽槽深为变量进行优化设计。将表3中数据进行多元二次方程回归分析，分析结果如表4所示。

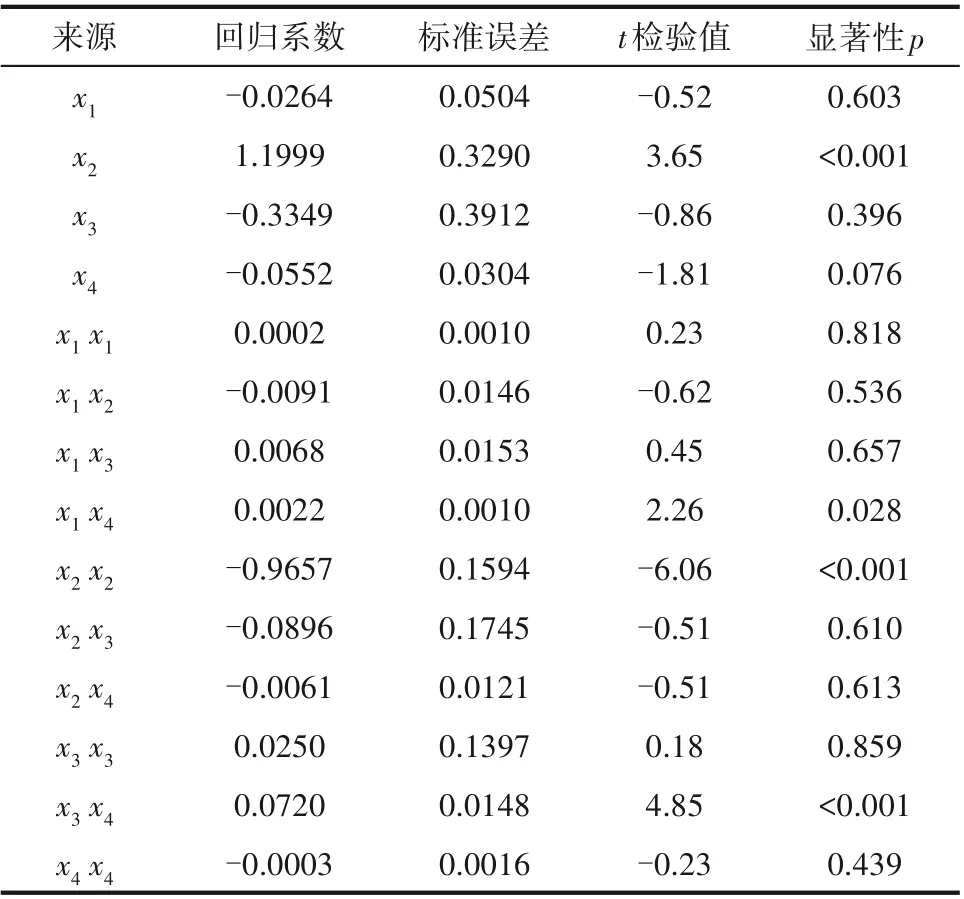
表4 系数显著性分析Table 4 Coefficient significance analysis

通过对表3 中数据进行多元回归分析，发现模型调整后的拟合优度R2接近1，且显著性p＜0.0001，这说明该模型在实验设计范围内回归显著。虽然模型总体显著性较好，但是不能说明所有因素项显著性都很明显，需要显著性检验，结果如表4 所示。从表中可以看出，槽堰比与螺旋槽槽深之间的两两交互作用非常明显（p＜0.001），螺旋角与槽深之间的两两交互作用显著（p≤0.05），其余项的交互作用不显著。

表3 中回归系数为多元二次方程自变量系数，上游泵送螺旋槽机械密封平均汽相体积分数模型即为式(7)

4.2 遗传算法及优化求解

利用仿真数据拟合得到的平均汽相体积分数与自变量型槽结构参数之间的多元二次方程关系式无法直接求解在变量范围内的最优解，本文利用Matlab 遗传算法工具箱进行辅助求解，遗传算法相较于其余常规算法，更适用与求解较为复杂的组合优化问题。

遗传算法具体流程如图6所示。

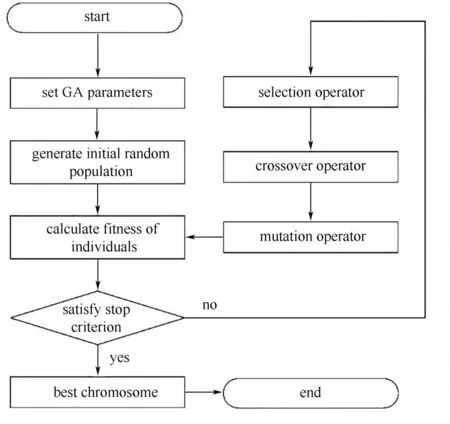
图6 遗传算法优化程序框图[38]Fig.6 Program chart of genetic algorithm optimization[38]

（1）初始化设置：设置进化迭代数计数器t=0，最大迭代数为G，随机生成N个个体作为初始值P(0)。

式(6)中包含4个自变量，根据常用和研究经验，各自变量参数范围分别为：x1选取螺旋角，取10°～30°；x2选取槽径比，取0.1～0.9；x3选取槽堰比，取0.1～0.9；x4选取螺旋槽槽深，取3～15 μm。约束如矩阵A、b及式（8）所示。

（2）个体评价：计算群体P(t)中各个个体的适应度，本文选取式(7)作为个体的适应度函数。

（3）选择运算：将选择算子作用于群体。交叉运算：将交叉算子作用于群体。变异运算：将变异算子作用于群体。通过带有猜测性质三种运算将群体P(t)推进到下一代群体P(t+1)。

（4）终止条件判断：若t≤G，则t=t+1，并计算群体P(t+1)中各个个体的适应度。若t＞G，则终止计算，选取此前过程中计算得到最大适应度的个体作为最优解。

因为汽液两相流机械密封在工作时，要保证密封稳定运行就需要对密封运行时的状态进行限定，一旦平均汽相体积分数超过最大汽相体积分数，密封就处于似汽相混相密封，液膜会出现不稳定，最终造成密封失效，而处于似液相混相密封时密封性能良好。所以根据顾永泉[39]提出的液态水的最大膜压系数对应的汽相体积分数范围为10%～25%，这里为了确保密封不会因汽化出现失稳现象，选择10%作为约束条件，如式(9)所示。

根据给出的优化约束条件，最终终止判断条件变为，群体P(t)中个体的适应度满足约束条件，并记录其中具有最大适应度的个体。通过多次迭代计算，最终得到端面型槽组合优化结果，其中，螺旋角最优范围为25.0°～28.0°；槽径比最优范围为0.10～0.30；槽堰比最优范围为0.10～0.25；槽深最优范围为4.0～6.0 μm。在本文给定工况范围内，当槽型结构参数在上述范围内选取，计算得到的平均汽相体积分数都小于最大膜压系数对应的汽相体积分数，使得密封稳定运行。

5 结 论

本文计算分析了传质系数对螺旋槽机械密封液膜相变的影响，并基于优化的传质系数计算分析了端面型槽结构参数对端面间液膜密封性能影响规律及各结构参数间交互影响规律，得到以下结论。

（1）随着传质系数的增加，平均汽相体积分数先随之增大后趋于平稳，传质系数的影响不可忽略；

（2）显著性分析结果表明，槽径比对平均汽相体积分数影响极其显著（p＜0.001），螺旋角、槽堰比及槽深对平均汽相体积分数影响较显著（p≤0.05）；交互项中槽堰比和槽深交互影响极其显著（p＜0.001），螺旋角和槽深交互影响较为显著（p≤0.05），其余交互项的交互影响不显著（p＞0.05）;

（3）平均汽相体积分数随着螺旋角、槽堰比、槽深的增大而增大，随着槽径比的增大先增加再减小。槽深越深，平均汽相体积分数随螺旋角及槽堰比的增大显著增加;

（4）研究多因素共同作用及交互作用对平均汽相体积分数影响十分必要，相较于单一因素的影响更准确。通过遗传算法分析得到螺旋角最优范围为25.0°～28.0°；槽径比最优范围为0.10～0.30；槽堰比最优范围为0.10～0.25；螺旋槽槽深最优范围为4.0～6.0 μm。