超临界二氧化碳垂直管内传热恶化数值模拟研究

汪森林，李照志，邵应娟，钟文琪

（东南大学能源热转换及其过程测控教育部重点实验室，江苏 南京 210096）

引 言

双碳目标对我国现有的能源结构提出了新的要求，以超临界水为工质的传统蒸汽循环燃煤发电机组受到材料耐高温耐腐蚀等因素的限制，其发电效率最高仅能达到47%[1]。相对于水，超临界二氧化碳（S-CO2）具有能量密度大、化学性质稳定、对应发电设备尺寸小、流动性与传热特性良好等优势，以CO2为工质的超临界二氧化碳布雷顿循环燃煤发电系统作为一种新型燃煤发电系统，在解决材料耐高温耐腐蚀问题的同时，有效减小了设备尺寸，结构更加紧凑。此外，相较于蒸汽朗肯循环发电系统，超临界二氧化碳布雷顿循环工质温度在620～650℃时，其理论发电效率可达50%以上[2]。因此，采用超临界二氧化碳布雷顿循环代替蒸汽朗肯循环能够实现热工高效转换，具有广阔的发展前景[3]。

在S-CO2布雷顿循环燃煤发电系统中，锅炉设计过程面临炉膛内较高的温度引起的受热面温度偏高与烟气侧烟气需要跨越宽温区等问题[3-4]，此外，在S-CO2启动端，其热力学状态处于跨临界区，使其热物性发生剧烈变化，该特性容易导致传热恶化，引起局部壁面温度的异常升高，甚至超温爆管，对系统安全运行造成不利影响。因此，全面了解S-CO2在跨临界区域传热流动的传热恶化发生的条件与机理，对超临界布雷顿循环燃煤发电系统内安全运行与水冷壁的设计具有重要意义。

现有关于S-CO2管内流动传热过程的传热特性的研究集中在压力、质量流量、热通量、管径以及热物性变化引起的浮升力效应与流动加速效应等因素。其中，实验研究主要包括压力、质量流量、热通量与管径等参数对传热特性的影响。Bae 等[5]研究在内径为6.32 mm 的垂直上升管内，不同压力对S-CO2传热特性的影响，结果表明，更高的压力导致更高的壁温和相应的更低的对流传热系数，但几乎没有改变对流传热系数的大小和范围。随着热通量的增加，壁温与对流传热系数的差异变得更加显著。Kim 等[6]在内径9 mm，压力分别为8.12 与8.85 MPa，质量流量为400 kg/(m2·s)工况下，进行热通量对S-CO2传热特性的影响实验，随热通量增大，壁面温度升高，并出现了壁温峰值，即从正常传热向传热恶化转变，且壁温峰值随热通量增大向靠近进口处移动。在压力与热通量均较高时，壁面温度出现了两个峰值。吴新明[7]在内径为10 mm 圆管内，关于质量流量对S-CO2传热特性影响的实验结果表明，低质量流量工况下，在进口处出现了明显的壁温峰值，对流传热系数出现了谷值，即发生了传热恶化，增大质量流量后，壁面温度降低，且壁温峰值消失，传热系数随沿程变化出现微小的波动，即传热模式由传热恶化向正常传热转变。Song 等[8]比较了S-CO2在内径为4.4 和9 mm 的两个圆管内垂直向上流动的传热行为；结果表明在9 mm 圆管内观察到明显的壁温峰值，发生了传热恶化，而在相同质量流量和热通量下，4.4 mm 管内，壁面温度仍缓慢升高，未发生传热恶化。然而，Liao 等[9]在不同管径内开展S-CO2传热特性实验得到了相反的结果：随管径增大，管内对流传热系数先增大后减小。文献[10-13]虽然报道了大量运行参数对S-CO2的影响，但主要集中于小管径（0～6.5 mm），对于大管径的研究较少。此外，由热物性变化引起的浮升力效应与流动加速效应也对传热恶化有重要影响，而由于SCO2管内传热特性实验条件下测量难度较大，无法获得其流场结构和S-CO2物性变化与其换热性能的关系，通过数值模拟可以有效解决这一问题。Zhang 等[14]通过评估SSTk-ω、Standardk-ω、Standardk-ε等7种湍流模型对S-CO2垂直圆管流动传热特性模拟的准确性，结果显示v2f 模型与SSTk-ω分别适用于低质量流量与一般质量流量工况。张良等[15]通过实验与数值模拟的方法研究了垂直上升管内S-CO2传热特性，分析了温度、密度、比热容、流速等截面参数变化对传热的影响，并从微观层面解释了传热恶化机理。庄晓如等[16]对垂直高温吸热管进行数值模拟，研究了浮升力效应与流动加速效应对传热特性的影响，发现在高热通量下，浮升力效应可以忽略，而流动加速效应会明显加剧传热恶化。Du 等[17]提出了变湍流Prandtl 数湍流模型，比较了包括正常传热与传热恶化的26 个实验工况；结果表明，变湍流Prandtl 数模型能够预测并再现传热恶化现象，在各种工况下具有较高的适用性。

准确预测传热恶化在工程应用方面具有重要意义，而运行参数是影响S-CO2管内流动传热过程的主要因素，因此，专家学者将发生传热恶化的最低热通量定义为临界热通量，并提出了相关预测关联式[18-23]，而现有预测关联式仅考虑了1～2个影响因素且多与质量流量呈线性关系。此外，由于适用的实验工况范围较窄，导致预测准确性差异较大。

本文针对现有临界热通量预测关联式适用实验工况窄、未综合考虑其影响因素等问题造成的预测关联式准确性差异较大的问题，开展S-CO2垂直上升管内传热流动数值模拟研究，首先研究了压力、质量流量、热通量和管径等运行参数对S-CO2垂直上升管内壁温与对流传热系数的影响规律，结合浮升力与流动加速效应揭示了不同运行参数下发生传热恶化的机理。然后，综合宽范围工况下的模拟结果，建立神经网络模型，提出了传热恶化临界热通量预测关联式，力求提高预测传热恶化的准确性。本文研究结果可为S-CO2布雷顿循环燃煤发电系统换热部件的设计与安全运行提供技术指导。

1 模型建立

1.1 物理模型及边界条件

本文对垂直上升管周向加热条件下的传热流动特性进行数值模拟研究，其几何模型如图1所示，实验段总长度为3 m，为保证管内流体充分发展，在进口段与出口段分别设置500 mm 的绝热发展段以避免进、出口效应，采用均匀恒定热流对实验段加热。

图1 物理模型Fig.1 Physical model

采用FLUENT软件进行数值模拟。进口边界条件设置为质量流量进口,出口设置为压力出口,加热段设置为恒定热通量,进出口的发展段均设置为绝热边界。CO2物性由NIST 软件导入。采用SIMPLE算法对速度与压力耦合进行计算处理，采用二阶迎风格式计算动量方程与能量方程，方程收敛残差均设置为10-6。

1.2 控制方程

根据Zhang 等[14]对不同湍流模型的评估结果，本文采用SSTk-ω湍流模型对S-CO2管内传热流动过程进行数值模拟，其控制方程主要包括连续性方程[式(1)]、动量守恒方程[式(2)]、能量守恒方程[式(3)]、湍动能方程[式(4)]以及比耗散率方程[式(5)]。

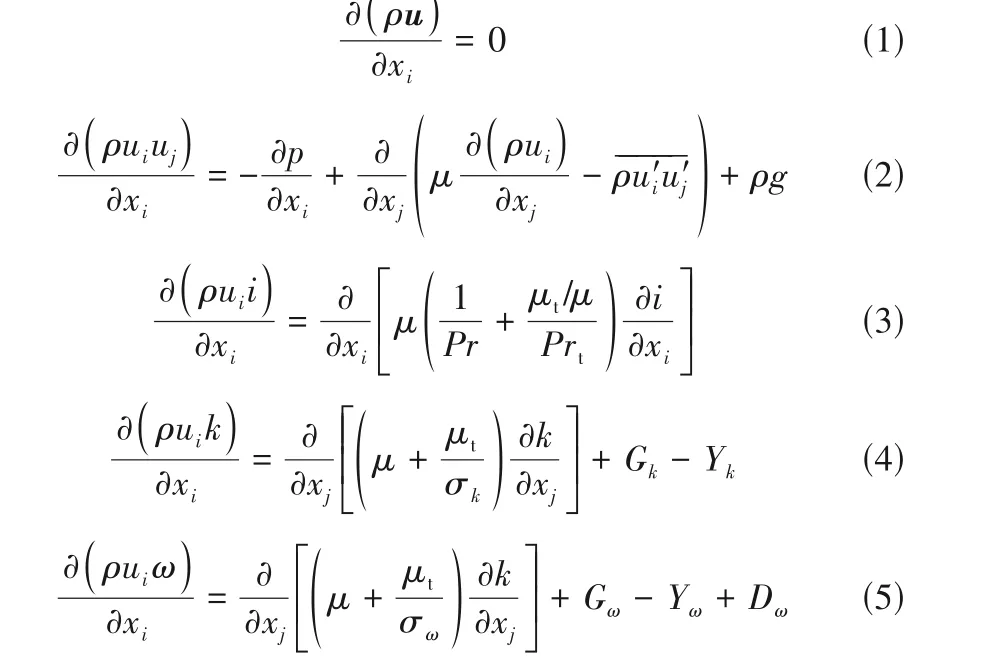
式中，u为速度矢量；ρ为工质流体的密度；p为压力；g为重力加速度；μ为黏性系数；μt为湍流黏性系数；Pr为Prandtl数；Prt为湍流Prandtl数；Gk为由速度梯度产生的湍动能；Yk、Yω分别为由于湍流产生的k、ω的损耗；Gω为ω的产生项；Dω为交叉扩散项；σk、σω分别为湍动能与耗散率对应的Prandtl数。

1.3 网格划分及无关性验证

根据张宇等[24]和朱兵国[25]的研究结果，S-CO2垂直上升管流动传热过程，可简化为二维轴对称模型。本文将计算模型简化为二维轴对称模型，采用ICEM-CFD 软件进行网格划分。为满足湍流模型的计算要求，令壁面第一层网格厚度为1×10-5m，边界层加密比例为1.1，以保证近壁面第一层网格的无量纲厚度y+小于1。

对七种不同网格数的网格模型进行计算，比较不同网格数下，加热段沿程壁面温度变化，如表1 所示。Case 5 与Case 7 的最大壁温偏差为0.03%，因此，本文同时考虑到计算精度与计算时长的因素，选择网格数为156100 个的网格进行后续的研究。

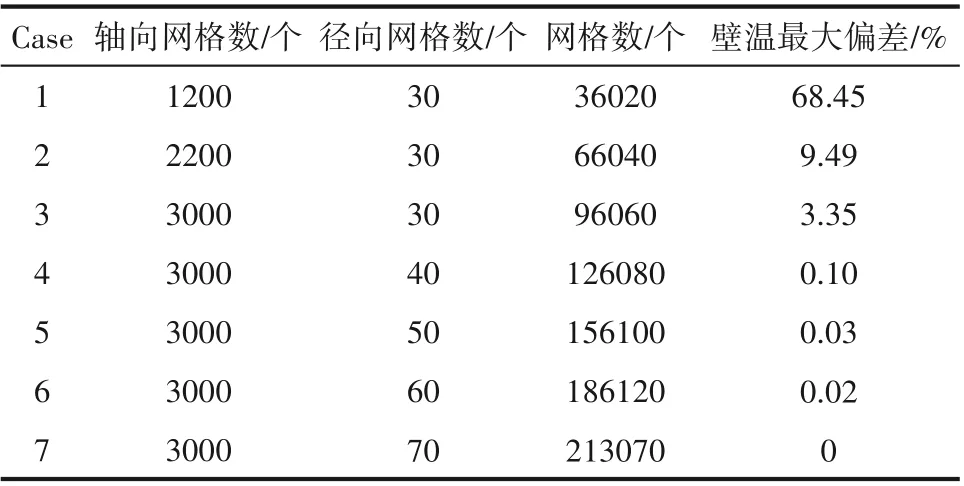
表1 网格无关性验证结果Table 1 Verification for grid independence

2 模型验证

为保证本文数值模拟方法的准确性，对张良等[15]与朱兵国[25]的实验工况进行数值模拟并与实验结果进行对比，选取工况如表2所示。

表2 模型验证工况Table 2 Model verification conditions

结果如图2所示，从计算结果可以看出，实验与数值模拟所得结果相一致，且最大误差不超过10%，因此，本文采用的数值模拟方法可以用于S-CO2管内传热流动特性研究。

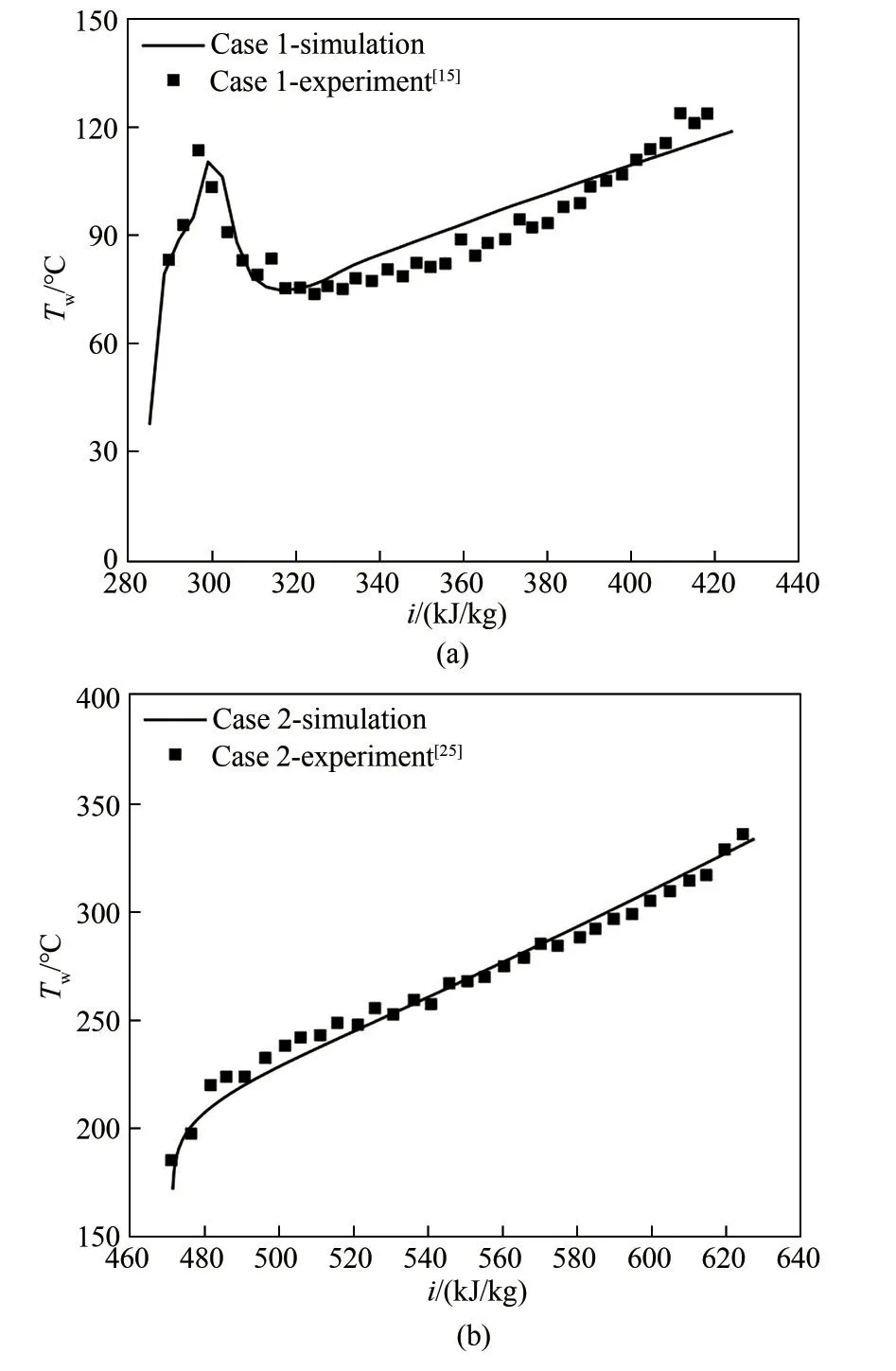
图2 模型计算结果与文献数据对比Fig.2 Comparisons between numerical results and experimental data

3 结果与讨论

3.1 运行参数的影响

3.1.1 压力的影响 图3所示为质量流量400 kg/(m2·s),热通量60 kW/m2,内径10 mm 的垂直上升管内，不同压力下S-CO2管内流动传热过程壁温与对流传热系数的沿程分布情况（其中，x为沿程距进口的距离，d为管径）。

从图3 中可以看出，当压力为11.07 MPa 时，沿程壁温分别在x/d=25 与x/d=80 处存在两个峰值，压力升高至14.78 MPa，壁温峰值只存在于进口处，且向远离进口方向移动至x/d=40 处，进一步提高压力到18.45与22.14 MPa，壁温峰值消失，传热恶化转变为正常传热。在x/d＞100 后，壁温均随沿程增加而缓慢增大，且壁温随压力升高而升高。对流传热系数则与壁温呈现相反的趋势，在11.07 与14.78 MPa工况下壁温峰值对应位置出现谷值。18.45 与22.14 MPa工况下，在x/d＜100时，对流传热系数随沿程增大而减小，x/d＞100后趋于稳定且随压力升高而减小。这一结果与Xu 等[26]的实验结果相一致。压力接近临界压力时，由于S-CO2热物性在拟临界温度会发生剧烈变化，导致壁温急剧升高，出现局部壁温峰值，随压力升高，拟临界温度升高，使得壁温峰值向远离进口方向移动，此外，S-CO2比热容与黏度等热物性变化随压力升高趋于平缓，使传热过程趋于稳定，这也是在高压力工况下未出现壁温峰值的原因，这表明，提高压力可以降低传热恶化程度，甚至消除传热恶化。

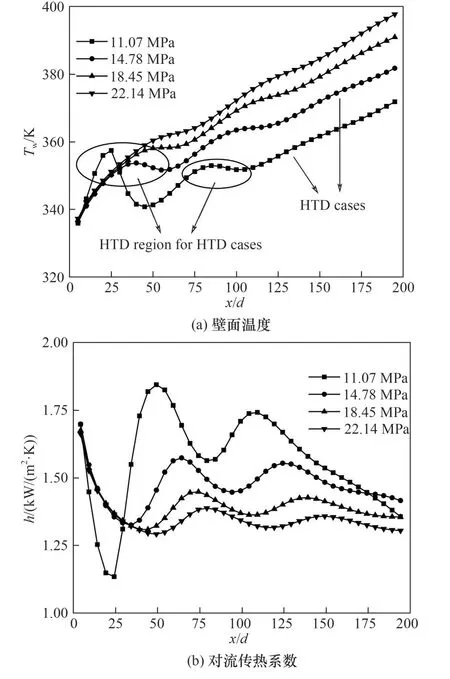
图3 压力的影响Fig.3 Effect of pressure

3.1.2 质量流量的影响 图4所示为压力22.14 MPa、热通量60 kW/m2、内径10 mm 的垂直上升管内，不同质量流量下S-CO2管内流动传热过程壁温与对流传热系数的沿程分布情况。

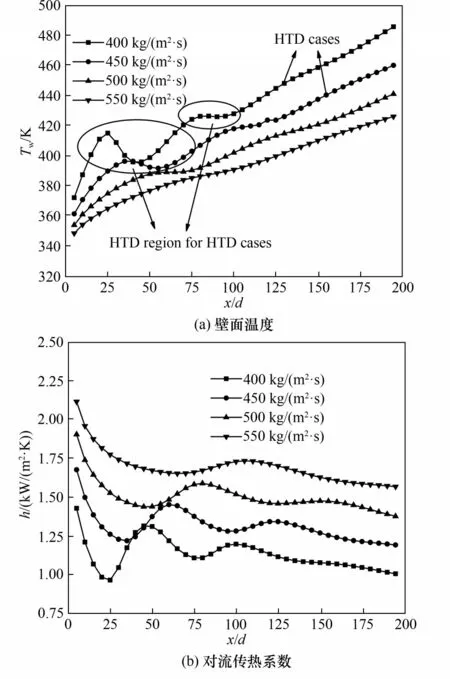
图4 质量流量的影响Fig.4 Effect of mass flux

从图中可以看出，随质量流量增大，壁温降低，对流传热系数增大。质量流量为400 kg/(m2·s)时，沿程壁温分别在x/d=25 与x/d=75 处存在两个峰值，对流传热系数在对应位置出现两个谷值。当质量流量增大至450 kg/(m2·s)时，沿程壁温峰值减少为一个，且壁温峰值相较400 kg/(m2·s)时的第一个峰值向远离进口处移动，对流传热系数在对应位置出现谷值。随质量流量继续增加至500与550 kg/(m2·s)时，壁温随沿程增大而缓慢升高，且未出现壁温峰值，对流传热系数先减小后趋于稳定。这一结果与王振川[27]的实验结果相一致。增大质量流量，使得S-CO2的湍流扩散速率增大，增强了其传热性能，导致壁面温度降低，对流传热系数增大。此外，增大质量流量也减小了壁面边界层厚度，降低了热阻，从而进一步增强了其传热性能。这表明，增大质量流量，可以降低传热恶化程度，甚至消除传热恶化。

3.1.3 热通量的影响 图5 所示为压力22.14 MPa、质量流量500 kg/(m2·s)、内径10 mm 的垂直上升管内，不同热通量下S-CO2管内流动传热过程壁温与对流传热系数的沿程分布情况。

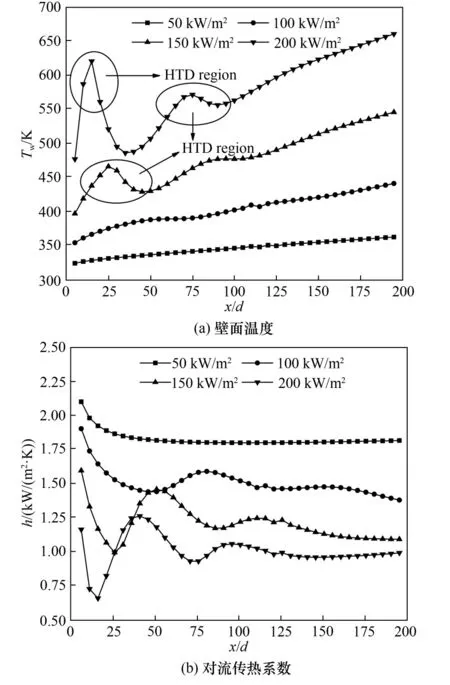
图5 热通量的影响Fig.5 Effect of heat flux

从图中可以看出，随热通量增大，壁温升高，对流传热系数减小，这与朱兵国等[28]的实验结果相一致。热通量为50 kW/m2时，壁温随沿程缓慢升高，对流传热系数先减小而后趋于稳定。当热通量增加至100 kW/m2，壁温相对50 kW/m2工况下升高，仍随沿程增大缓慢升高，对流传热系数缓慢减小。进一步提高热通量至150 kW/m2，沿程壁温在x/d=25处出现峰值，在x/d＞50 后随沿程增加缓慢升高。对流传热系数在对应位置出现谷值，并在x/d＞50 后随沿程增加缓慢减小。当热通量提高至200 kW/m2，沿程壁温分别在x/d=15 与x/d=75 处出现两个壁温峰值，在x/d＞100 后，壁温随沿程增加缓慢升高。对流传热系数在对应位置分别出现两个谷值，并在x/d＞100后随沿程增加缓慢减小。在150与200 kW/m2工况下发生传热恶化现象的原因在于较大的热通量使得近壁面流体温度急剧升高，流体径向密度分布不均匀引起浮升力效应以及体积膨胀引起流动加速效应，湍流强度降低，导致湍流层流化，从而削弱传热性能。这表明，提高热通量会加剧传热恶化。

3.2 管径的影响

图6 所示为压力22.14 MPa，质量流量400 kg/(m2·s),热通量95 kW/m2的垂直上升管内，不同管径下S-CO2管内流动传热过程壁温与对流传热系数的沿程分布情况。

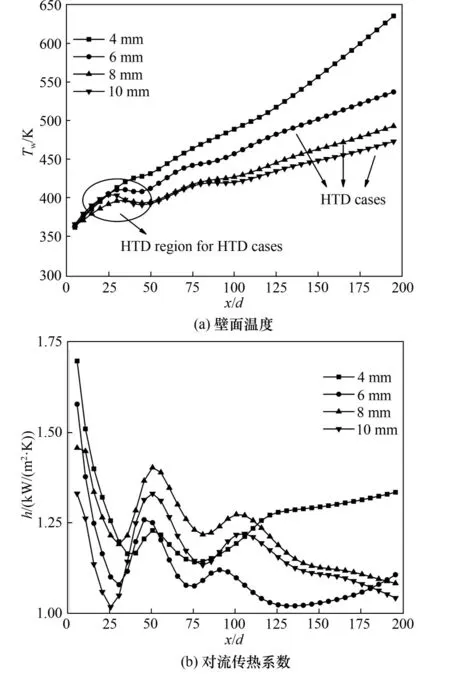
图6 管径的影响Fig.6 Effect of diameter

从图中可以看出，随管径增大，壁温降低，而对流传热系数变化较小。管径为4 mm时，随沿程增加壁温缓慢升高，对流传热系数先减小然后趋于稳定。增大管径至6 mm 时，沿程壁温在x/d=30 处出现壁温峰值，在x/d＞50 后随沿程增大而缓慢升高，对流传热系数在对应位置出现谷值，随后在x/d＞50后随沿程增大先减小然后趋于稳定。进一步增大管径到8 与10 mm，发现二者沿程壁温较为接近，8 mm 管径下壁温峰值出现在x/d=30处，而10 mm 管径壁温峰值出现在x/d=25 处，且峰值温度略高于8 mm 管径，对流传热系数分别在对应位置出现谷值，在x/d＞50 后，二者对流传热系数均随沿程增加而减小，且8 mm 管径下的对流传热系数略高于10 mm 管径。值得注意的是，4 mm 管径下，虽未发生传热恶化，对流传热系数仍存在波谷，这是由于管径较小时，浮升力作用更为显著。此外，进口边界条件均设置为质量流量，小管径则具有更大流速，流动加速效应增强，且浮升力与流动加速效应在垂直上升管内方向相同，削弱了传热，使得对流传热系数减小。增大管径，一方面，增大了S-CO2对流换热面积，使得换热增强；另一方面，由于浮升力作用，传热性能得到削弱。在二者的综合作用下，增大管径削弱了传热性能。

3.3 浮升力与流动加速的影响

浮升力与流动加速效应通过改变管内流场结构对S-CO2的传热特性产生重要影响，本文采用Jackson 等[29]与McEligot 等[30]提出的判据，研究不同运行参数下浮升力与流动加速对垂直上升管内SCO2传热特性的影响。浮升力特征数(Bu)与流动加速特征数(Kv)表达式如下：

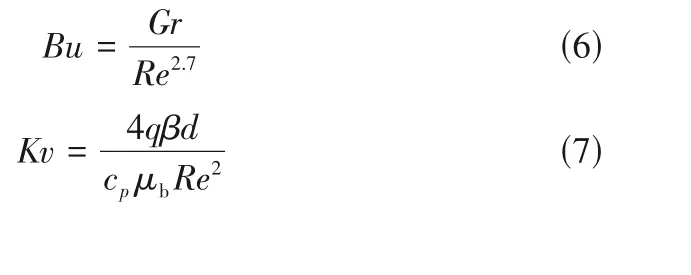
其中：

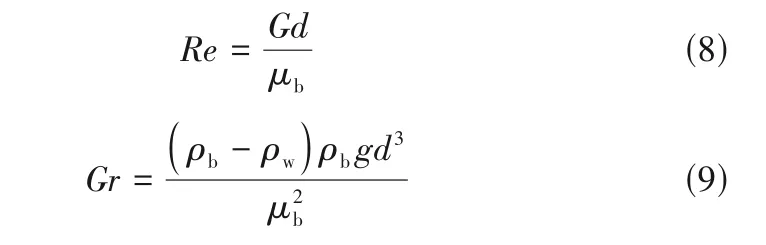
式中，Bu的阈值为10-5，Kv的阈值为3 × 10-6。

3.3.1 浮升力的影响 图7给出了不同运行参数下Bu随沿程的分布情况。从图7（a）中可以看出，在x/d＜100 区域内，Bu随压力升高而减小，而在x/d＞100区域则出现相反的趋势。图7（b）所示为质量流量对Bu的影响，随质量流量增大，Bu减小，且在大质量流量下，Bu变化量减小。从图7（c）中可以看出，随热通量增大，Bu逐渐出现峰值，且更为显著，并向靠近进口处移动。图7（d）所示为管径对Bu的影响，随管径增大，Bu增大，且峰值向远离进口处移动。值得注意的是，虽然所有工况下Bu均大于阈值，但传热恶化工况下，Bu峰值在沿程位置上与壁温峰值相对应，这表明传热恶化能够通过浮升力效应反映，但其阈值的确定仍需进一步研究。

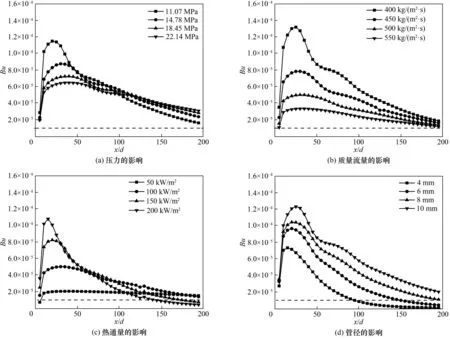
图7 运行参数对Bu的影响Fig.7 Effect of operating parameters on Bu

3.3.2 流动加速的影响 图8给出了不同运行参数下Kv随沿程的分布情况。从图中可以看出，随压力升高Kv增大，且在不同压力下，Kv均随沿程增加而减小。随质量流量增大，Kv减小，且在不同质量流量下，Kv均随沿程增加而减小。随热通量增大，Kv增大，且在200 kW/m2工况下，Kv随沿程增加先减小后增大，其余工况下，Kv均随沿程增加而减小。与热通量相反，Kv随管径增大而减小，且在4 mm 工况下，Kv随沿程增加先减小后增大，其余工况下，Kv均随沿程增加而减小。此外，在所有工况下，Kv均低于阈值，这表明在垂直上升管内，流动加速效应对S-CO2管内对流传热过程的影响可以忽略。

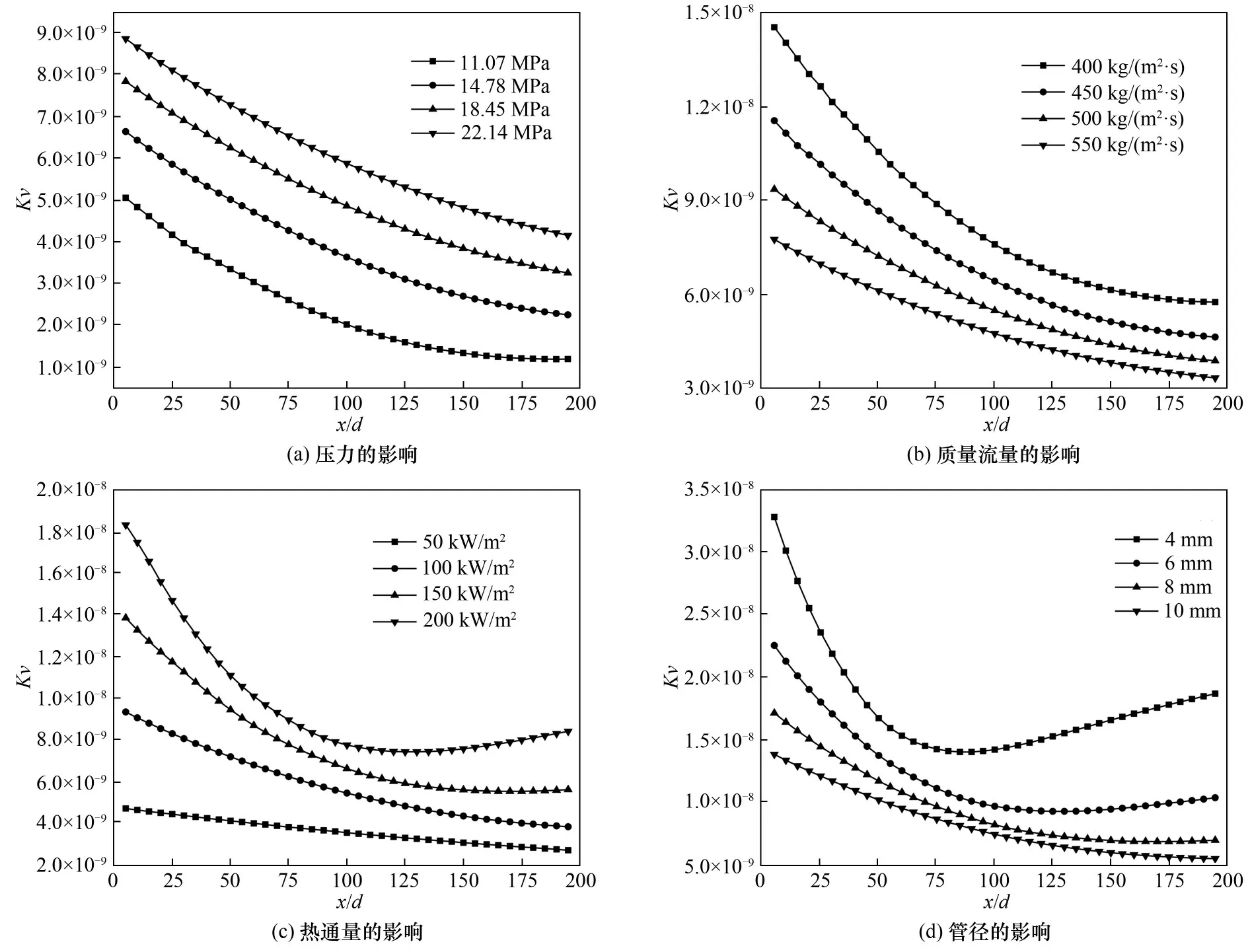
图8 运行参数对Kv的影响Fig.8 Effect of operating parameters on Kv

3.4 传热恶化预测关联式

为准确预测S-CO2管内传热行为，本文基于数值模拟计算结果（工况范围如表3 所示），采用TensorFlow 机器学习库建立深度神经网络模型（DNN），如图9 所示，计算模型包含输入层、隐藏层与输出层。输入层为压力、质量流量与管径等运行参数，输出层为临界热通量，其算法为：

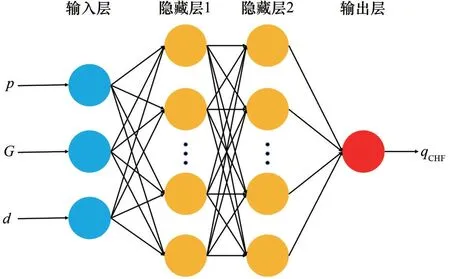
图9 神经网络结构Fig.9 Neural network structure

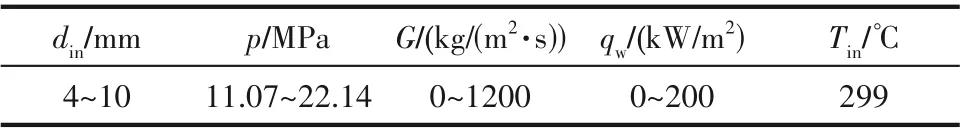
表3 数值模拟计算工况Table 3 Numerical simulation calculation conditions

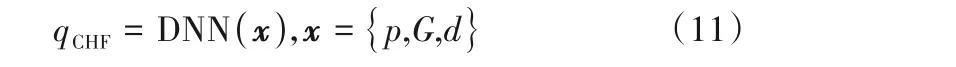
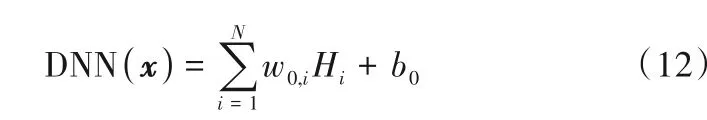
式中，qCHF为临界热通量；x为输入向量；Hi为隐藏层单元；w0,i为权重系数；b0为偏差参数。

计算收敛后所得临界热通量预测关联式如下：

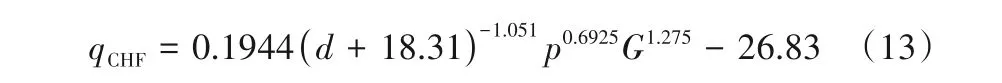
对于给定工况下的实际热通量，可以根据以下方式判断预测的正确性：

（1）若给定工况为非传热恶化工况，且预测热通量大于实验热通量，则视为判断正确，反之则视为判断错误；

（2）若给定工况为传热恶化工况，且预测热通量小于实验热通量，则视为判断正确，反之则视为判断错误。

定义预测准确率为：

式中，N为实验工况点总数；n为判断正确工况总数。

本文根据Duffey等[31-32]提出的传热恶化定义，若壁面出现峰值则为传热恶化，否则为正常传热。通过收集现有文献[5-6,11,13-26,27-44]中实验数据用于验证本文提出关联式的准确性，所有实验数据均来自垂直上升管。压力范围为7.5～21.14 MPa，质量流量范围50～2716 kg/(m2·s)，管径为0.27～22 mm，热通量为2.9～549 kW/m2，共337个工况点。其中，传热恶化工况点211 个，非传热恶化工况点126 个,结果如表4、图10所示。

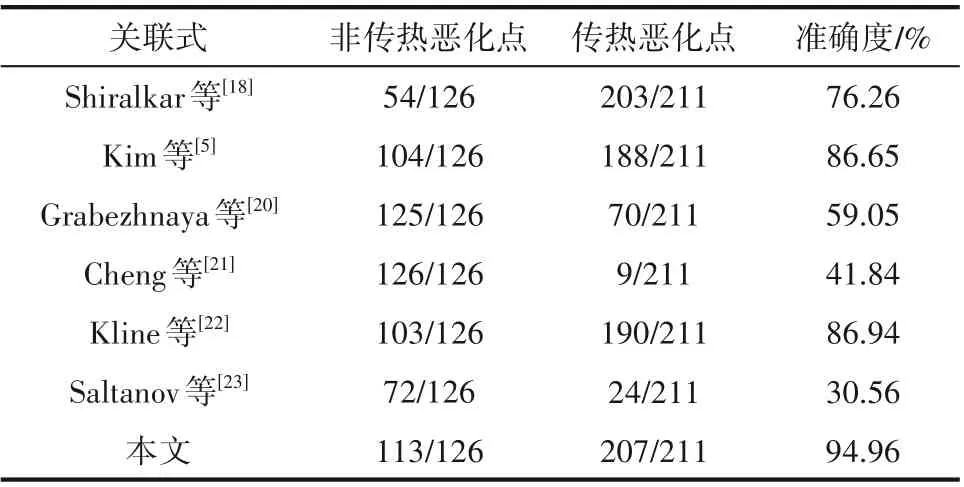
表4 预测关联式准确性Table 4 Accuracy of correlations

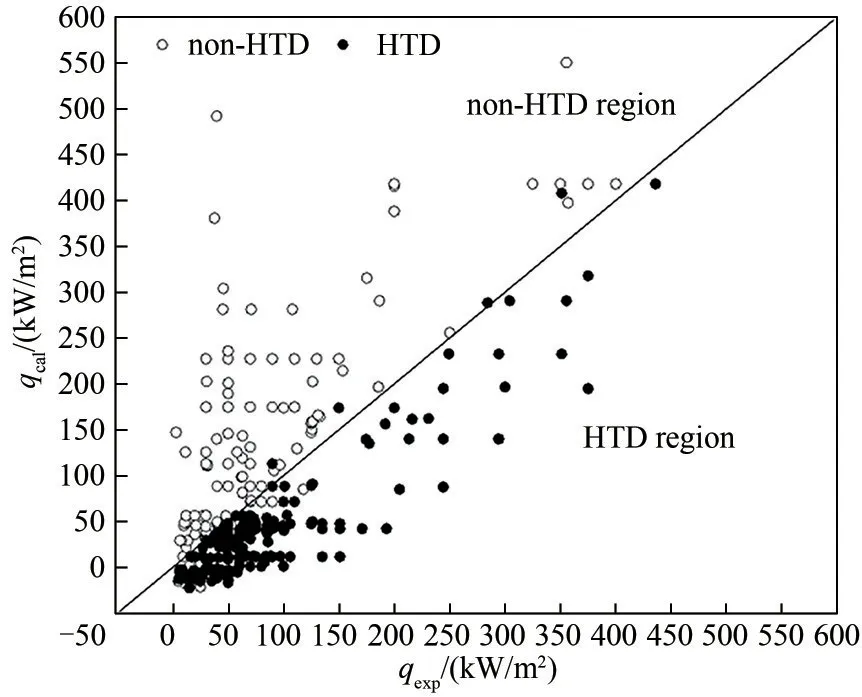
图10 预测关联式与实验值比较Fig.10 Comparison between correlation and experimental data

从表4中可以看出，Shiralkar 等[18]准确预测传热恶化工况，但非传热恶化工况预测准确性较低；Grabezhnaya 等[20]与Cheng 等[21]提出的关联式则只能准确预测非传热恶化工况，均过于保守。Kline 等[22]提出的关联式由于考虑了管径的影响，其准确度较高。本文综合考虑压力、质量流量、管径与临界热通量的关系提出的预测关联式具有94.96%的准确度，且在两类工况下的预测中均有较高的准确性，因此，可以用于预测S-CO2管内传热流动过程的传热行为。

4 结 论

本文对S-CO2锅炉内垂直上升管的流动传热特性开展数值模拟研究，分析了压力、质量流量、热通量以及管径等运行参数对壁面温度与对流传热系数的影响，讨论了浮升力与流动加速效应对传热的影响，并提出新的临界热通量预测关联式，得出以下结论。

（1）对于S-CO2垂直上升管内流动传热过程，提高压力与质量流量，沿程壁温峰值向远离进口方向移动，其数值逐渐减少并消失，传热恶化程度降低；提高热通量与管径，壁面温度升高，对流传热系数减小，壁温峰值逐渐增加且壁温峰值向进口方向移动，传热恶化程度加剧。

（2）对于S-CO2垂直上升管内流动传热过程，浮升力效应对传热恶化具有显著作用，而流动加速效应对其传热特性的影响可以忽略。

（3）综合考虑压力、质量流量、管径与临界热通量的关系，本文提出临界热通量的预测关联式，准确度达到94.96%，可用于预测S-CO2管内传热流动过程的传热行为。

符 号 说 明

cp——比定压热容，kJ/(kg·K)

G——质量流量，kg/(m2·s)

Gr——Grashof数

H——隐藏层单元

h——对流传热系数，kW/(m2·K)

r——实验段圆管半径，m

w——权重系数

下角标

b——主流

cal——计算值

exp——实验值

w——壁面