链接数学实验,让思维拔节生长
——《长方形和正方形的面积》教学设计(一)
文|陈美华
【教学内容】
苏教版三年级下册第66~68页。
【教学过程】
一、复习激活,渗透方法
1.基础复习。
师:我们学过了哪些面积单位?怎样的正方形面积正好是1平方厘米、1 平方分米、1 平方米?
2.看图口答。
师:下面图形的面积是多少?(每格是1 平方厘米的正方形)

生:它们的面积分别是9 平方厘米、10 平方厘米、15 平方厘米,我是用数格子的方法得到的,可以从左往右数或从上往下数,有几个格子面积就是几平方厘米。
生:第三幅图也可以先数再算,因为它是长方形,先数出每排有5 个,有这样的3 排,再用3 乘5 得15,一共有15 格,所以面积是15 平方厘米。
师:通过数一数或数数算算,你们都有什么发现呢?
生:有几个1 平方厘米,它们的面积就是几平方厘米。
师:一个图形含有面积单位的个数就是这个图形的面积。
二、实验探究,发现方法
1.初次实验,引发猜想。
(1)启发思考,自主探究。
师:这里有两个没有分好格子的长方形,想知道它们的面积有什么好办法呢?(揭示课题:长方形的面积)
生:可以用尺去量一量长方形的长、宽是多少厘米,然后分成1 平方厘米的正方形格子,数数算算有几格,面积就是几。
生:我看到学具盒里有1 平方厘米的小正方形,可以用它去摆一摆、量一量,也可以知道长方形的面积。
师:(出示《实验记录单一》)同学们都有了自己的想法,那就开始行动吧!
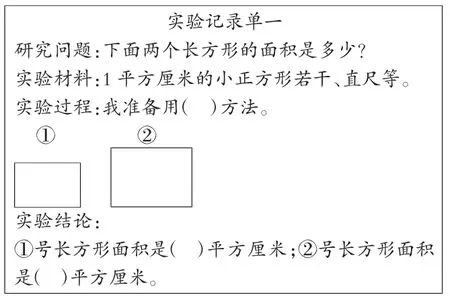
(2)发散思考,交流分享。
师:同学们都有自己的收获了吗?来和大家分享一下吧。
生1:我是用小正方形去摆的。①号长方形每排摆4 个,摆了3排,用了4 乘3 一共12 个1 平方厘米的小正方形,所以面积是12平方厘米;②号长方形每排摆5个,摆了4 排,用了5 乘4 一共20个1 平方厘米的小正方形,所以面积是20 平方厘米。(如下图)

师:还有不同的方法吗?
生2:我先用尺量出两个长方形的长和宽,再在边上每1 厘米处点上标记,用尺连线将长方形分成1 平方厘米的小正方形,再用每排的个数乘排数就算出了两个长方形的面积。(如下图)
师:生2 用了分一分的方法,与生1 的方法有什么相同之处吗?
生:我认为生2 的方法其实也相当于用1 平方厘米的小正方形摆满了,再数一数、算一算的。
师:是呀,透过现象看本质,都是摆满了再数数算算。还有谁想与大家分享自己的想法?
生:我也是用小正方形去摆的,我觉得不需要摆满,①号长方形只要像这样先摆一排4 个,再摆1 列就表示有这样的3 排,4 乘3得到面积是12 平方厘米;②号长方形每排摆5 个,再摆1 列就表示有这样的4 排,5 乘4 得到面积是20 平方厘米。(如下图)

师:在这些方法中你们比较欣赏哪一种呢?为什么?
生:我欣赏没有摆满的方法,根据摆的一排与一列的个数可以想象出长方形摆满的情况,所以这种方法巧妙而且花的时间少。
师:是呀,解决同样问题的方法也是有讲究的。
(3)比较思考,引发猜想。
师:回顾研究长方形面积的实验过程,你们还有什么发现呢?
生:我发现长方形中含有1 平方厘米的小正方形的个数就是它的面积。
师:对呀,长方形含有面积单位的个数就是它的面积。
生:我还发现它们的面积是每排的个数乘排数。
生:我发现长方形的面积等于长乘宽。
师:在课始“看图口答”第三个图形时大家也想到了这个方法,仅三个例子得到的方法一定正确吗?
生:不一定,我们还要举出更多的例子去验证。
师:确实由几个例子得到的发现只能作为猜想,我们还要举出更多的例子去验证。下面我们进入第二个实验。
2.再次实验,验证推理。
(1)实验探究,尝试验证。
师:(出示《实验记录单二》)一般要举几个例子才能说明问题?
生:至少三个,也可以更多。
师:表格的下面可以根据需要继续增加几行。下面继续你们的研究行动吧!
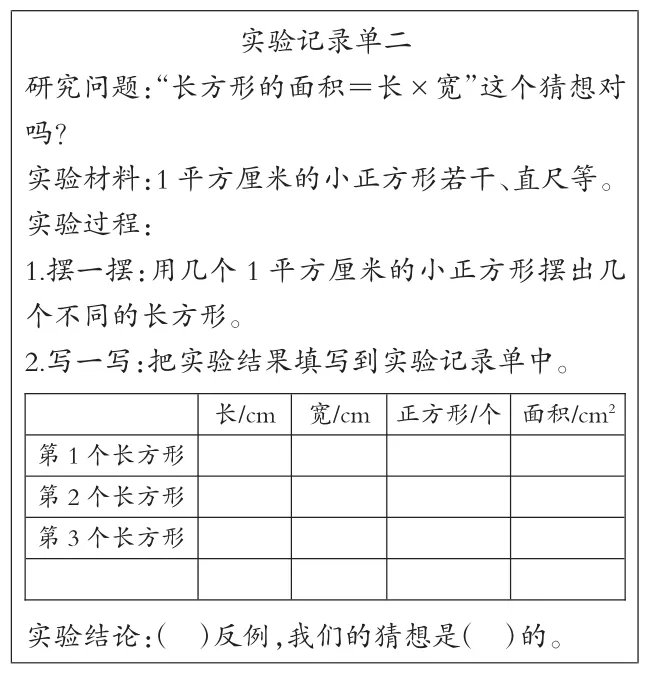
实验记录单二研究问题:“长方形的面积=长×宽”这个猜想对吗?实验材料:1 平方厘米的小正方形若干、直尺等。实验过程:1.摆一摆:用几个1 平方厘米的小正方形摆出几个不同的长方形。2.写一写:把实验结果填写到实验记录单中。长/cm 宽/cm 正方形/个 面积/cm2第1 个长方形第2 个长方形第3 个长方形实验结论:( )反例,我们的猜想是( )的。
(2)交流思辨,发现推理。
生:我摆了三个长方形,第一个长方形的长、宽分别是……我发现每个长方形所用小正方形的个数正好是长方形的面积,也等于长乘宽的积,所以我猜想“长方形的面积=长×宽”是正确的。(如下图)

生:我用了画图分格子的方法进行实验,先想好三个长方形的长、宽分别是几厘米,再画一画、分一分……也验证了我们的猜想是正确的。(如下图)
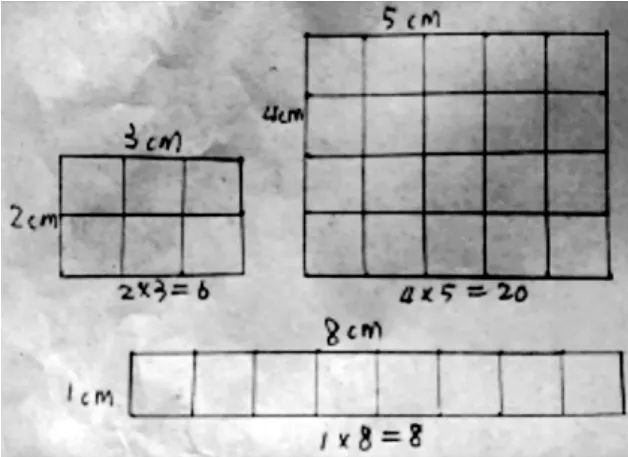
生:我没有摆满,像上次一样只摆了一排和一列,就想象出了长方形的长与宽,同样验证了我们的猜想是正确的。(如下图)

师:同学们很会动脑子,大多数用了简摆的方法去举例。每个同学都至少举了三个例子,合起来已经有很多不同的例子了,例子还可以继续举下去吗?
生:可以。
师:再举出10 个、100 个、1000 个乃至更多的例子,就能说明我们的猜想一定是正确的吗?
生:不太确定。
师:大家可以举出无数的例子,但还不能急于下结论,有时候还要寻找有没有反例,如果一个反例也找不到就能下结论了。大家找找看,有反例吗?
生:我们想到了比较特别的一种,就是摆一排的那种,每排不管是几个,1 乘几面积还是几,仍然验证了我们的猜想,找不到反例。
师:为什么找不到反例呢?能结合刚才你们的研究过程来说说理由吗?先自己想一想,再与小组同学说一说。
生:不管摆多少个长方形都可以发现,长方形含有小正方形的个数就是它的面积,而小正方形的个数等于每排的个数乘排数,每排的个数就是长方形的长,排数就是长方形的宽,所以长方形的面积就等于长乘宽。(相应完善板书,如下图)
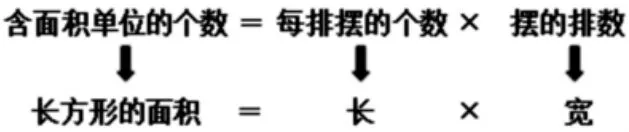
师:现在我们可以认为大家的猜想是正确的吗?
生:可以。
师:如果用S 表示长方形的面积,用a 和b 分别表示长方形的长和宽,公式怎么简写呢?
生:S=a×b。
(3)延伸拓展,整体建构。
师:同学们动手动脑自己研究发现了长方形的面积计算方法,正方形的面积计算方法又是怎样的?(课题补充:正方形)你能自己思考发现吗?先自己想一想,再与同伴交流一下想法。
(学生独立思考,小组交流)
生:我认为正方形的面积=边长×边长,因为正方形是特殊的长方形,当长方形的长和宽相等时,长方形就变成了正方形,只要将公式中的长方形改写成正方形,长和宽改写成边长就可以了。
生:我同意他的想法,我们可以想象,如果用边长1 厘米的小正方形去摆,就摆出了每排的个数等于排数的特殊情况,所以正方形的面积=边长×边长。
师:同学们根据长方形与正方形的关系推导出了正方形的面积计算公式,利用关系来推理也是很重要的本领,给自己鼓鼓掌!
师:如果用S 表示正方形的面积,用a 表示正方形的边长,公式又可以怎样简写?
生:S=a×a。
三、回顾反思,内化方法
师:通过刚才的学习研究,回顾一下长方形的面积公式是怎样推导出来的,正方形呢?
生:我们先通过几个例子的研究发现长方形的面积计算方法,由几个特殊例子得到的发现不一定正确,只能作为猜想,我们又举了更多例子去验证,并且找不到反例,最后得出结论。
生:我们还根据正方形与长方形的关系,推出了正方形的面积计算公式。
师:是呀,在许多数学方法或规律的学习中,都要经历这样的研究过程。
四、分层练习,拓展渗透
师:同学们自己研究发现了公式,要求长方形、正方形的面积需要什么条件?
1.看图计算。
教材第67 页“试一试”。
2.解决问题。
教材第68 页“想想做做”第1、2 题。
3.挑战自我。
下图中每个小正方形表示1平方厘米,你能算出两个长方形的面积吗?
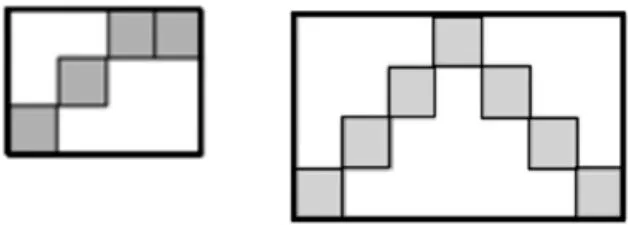
4.文化渗透。
师:我们的祖先早就研究过长方形的面积,方田术曰:广从步数相乘得积步。这里的方田就是长方形,广是长,从就是宽,也就是我们今天研究的:长方形的面积=长×宽。你们今天自己研究发现了这个方法,特别棒!
五、回顾反思,梳理内化
师:同学们通过今天的学习有什么收获?
师:同学们不仅知道并会运用长方形和正方形的面积计算公式,还知道这些公式是怎么研究发现的。相信大家带着这样的研究方法与科学态度,一定会发现更多的数学奥秘。

