基于动态谐波回归的超短期风电功率预测

王若谷，王 珂，戴立森，张 耀，孙宏丽，王建学

（1.国网陕西省电力有限公司 电力科学研究院，西安 710100；2.西安交通大学 陕西省智能电网重点实验室，西安 710049）

0 引言

随着能源危机与环境污染问题逐渐突出，世界多国开始大力发展清洁可再生能源，风电渗透率不断提高［1］。风能的高随机性使得风电具有高不可调度性，这为电力系统的安全稳定运行带来诸多挑战。准确地预测风力发电功率并将预测信息提供给调度部门可以有效地解决上述问题。风电功率的预测精度与预测提前期有关［2］。预测提前期越短，风速变化越小，预测精度也就越高。因此，4～6 h 内的超短期预测往往具有较好效果，通常风电超短期预测主要用于功率控制、实时调度［3］、风电场内部调度等。

为研究风电功率出力特性及其预测问题，国内外学者对此展开了深入的分析。从预测模型的角度，超短期风电功率预测方法可以分为物理预测法和统计预测法两大类。物理预测法［4］通过获取风电场的数值天气预报（numerical weather prediction，NWP），结合地势等地理因素，考虑风机轮毂高度等参数，建立包含大气运动、风电场以及风机等内容的综合物理模型达到预测目的，该方法更适合缺乏历史数据的新建风电场，但是建模过程和求解过程十分复杂，通常需要依赖超级计算机。物理预测法可以模拟未来数天的大气运动过程，因此更适用于提前期为24 h的短期风电功率预测［5］。统计分析法则完全依靠历史数据，通过数理统计或智能算法进行风电预测。该方法不需要像物理预测法那样复杂的数据类别，通常包括风速、历史风电功率等，构造的模型简单。研究表明此方法更适用于超短期风电功率预测［6］，但是由于其需要大量历史数据，因此不适合新建风电厂的使用。常用的统计分析方法包括回归法［7］、自回归移动平均模型（autoregressive integrated moving average model，ARIMA）［8—9］、卡尔曼滤波［10］、支持向量机［11］、神经网络［12］。回归方法由于其良好的物理解释性得到了广泛应用，但是该方法对风速预测值十分敏感。文献［7］提出NWP针对风电场轮毂高度的风速预报精度较差，因此采用线性回归方法对NWP提供的风速信息进行校正，从而减小风速预测值的不确定性，提高风电功率的预测精度。但是该方法仅从修正风速角度提升预测精度，而没有考虑到风电功率具有的数据特征，例如风电功率能量来源于风，与太阳辐射有密切关系，因此具有一定的周期性。另一方面，尽管ARIMA方法具有较高的风电功率超短期预测精度［9］，但是该方法仅仅依赖于风电功率的历史数据，而没有考虑到风电功率与风速的强相关性，因此其预测精度具有进一步的提升空间。

为充分利用风速预测信息与风电功率自身数据特征，本文提出利用动态谐波回归方法进行超短期风电功率预测。该方法采用风电功率与风速的三次多项式回归关系，考虑到回归残差具有高度的自相关性，使用ARIMA方法对回归残差进行建模，从而利用了风电功率数据的变化特性。此外针对风电功率具有的日季节性特点，引入傅里叶级数刻画该数据特征，进一步提高了超短期风电的预测精度。

1 数据来源与预处理

本文所用数据来自Global Energy Forecasting Competition 2014。该数据包括澳大利亚10 个风电场24 个月每天的风电出力数据与NWP 数据，时间分辨率为1 h，其中风电功率数据已被标幺化，NWP提供了10 m 与100 m 处的沿经度和纬度的风速（即UV风的风速）。

由于NWP 仅提供UV 风的预测信息，需要变换为常见的风速和风向，变换公式为

式中：υ为合成风速；φ为风向；u、v分别为沿经度和纬度的风速。

2 动态谐波回归模型的建立

本章首先介绍静态回归预测模型，然后通过ARIMA 方法对残差建模来刻画预测对象的动态特性，最后考虑预测对象具有的季节性，从频域角度引入傅里叶级数形成动态谐波回归模型。

2.1 静态回归模型

2.1.1 静态回归模型的建立

静态回归模型假设预测对象与预测变量存在某种映射关系，然后利用该映射关系以及预测变量的未来值进行预测。风力发电与风速具有明显的相关性［13］，文献［14］提出风机出力与风速具有三次多项式关系，即

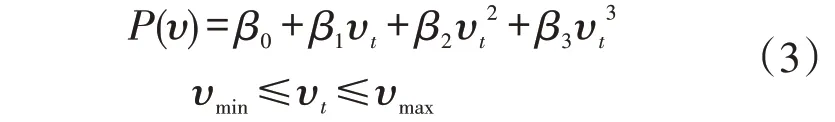
式中：β0、β1、β2和β3均为待估计参数；υmin、υmax分别为切入风速和切出风速。当风速小于切入风速时，风机出力为0；当风速大于切出风速时，风机出力达到额定值。

对于整个风电场而言，风电功率为所有风机出力之和，也近似满足式（3）的关系，故风电预测的静态回归模型可以表示为

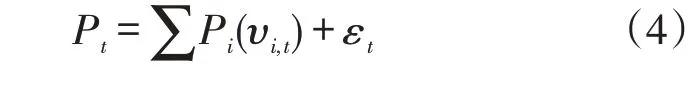
式中：Pt为预测对象，即风力发电功率；Pi为不同高度风速υi,t对风电功率的贡献且满足式（3）；在实际预测中，风速υi,t是未知的，需要通过NWP 获得；εt为残差并假设其是均值为0，方差为δ2的白噪声。

选择合理高度的风速作为预测变量是提高静态回归模型预测精度的重要手段。将具有最优回归效果的风速集合称为最佳回归子集。该模型的最佳回归子集可通过最大化可决系数、最小化信息准则或交叉验证等方法来确定［15］。

2.1.2 回归残差的假设检验方法

对回归结果的残差项进行Ljung-Box 检验可以判断其是否为白噪声［16］。Ljung-Box 检验基于一系列滞后阶数，判断时间序列总体是否存在随机性。原假设为原时间序列不具有自相关性，备择假设为原时间序列具有自相关性。构造统计量为

式中：T为样本数量；ρ(l)为样本l阶滞后的相关系数；L为被检验的滞后阶数；统计量Q服从自由度为L的χ2分布。给定显著性水平α，则拒绝域为。

若接受原假设，表示残差项不具有相关性，说明所建立的回归模型比较完整地刻画了预测对象与预测变量之间的关系。若拒绝原假设，则意味着原时间序列中仍有信息没有充分利用。

2.2 ARIMA动态回归模型

静态回归模型仅仅依赖预测变量，而没有考虑风电功率本身的动态变化过程。由于该预测模型没有充分利用风电功率时间序列的已知信息，因此静态回归的残差通常具有显著的自相关性，无法通过第2.1.2节介绍的Ljung-Box检验。

为解决上述问题，ARIMA 动态回归模型使用ARIMA方法对静态回归的残差项进行建模，从而能够有效地考虑风电功率时间序列的自相关性。

2.2.1 时间序列平稳性

静态回归的残差可以看作新的时间序列ΔPt，ARIMA方法要求残差时间序列具有平稳性，即该时间序列应具有不随时间改变的固定均值和方差。

单位根检验方法能检验时间序列的平稳性以及确定时间序列的差分次数d。本模型采用KPSS单位根检验方法［17］，采用模型为

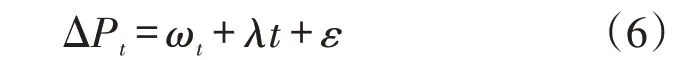
式中：λ为确定性趋势系数；ωt为随机游走过程；ε为稳定的误差。构造统计量为

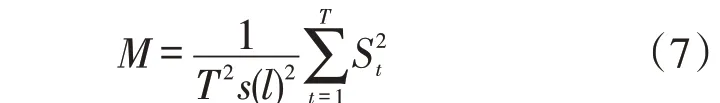
式中：T为样本容量；St为待检验残差和；s(l)2为残差的Newey-West估计；l为滞后阶数。给定显著性水平α，若M小于临界值则接受原假设，认为该残差序列平稳；否则，认为该残差序列不平稳，需要进行一次差分。差分后的残差序列需要再次进行单位根检验，直到稳定为止，从而确定出差分次数d。

2.2.2 残差的ARIMA模型

将经过d次差分、具有平稳性的残差序列记作则其ARIMA 模型为自回归模型（autoregressive model，AR）和滑动平均模型（moving average，MA）两部分之和，即

式中：c 为常数；Δ为平稳残差序列的滞后项；p为滞后阶数；εt为ARIMA模型的残差并假设其为一组均值为0、方差为δ，且相互独立的白噪声；q为ARIMA模型的残差滞后阶数；φp、θq分别为自回归参数和滑动平均参数。该模型表明静态回归的残差由两部分组成：发电功率的残差历史值以及ARIMA模型的残差历史值。

2.2.3 风电功率预测的动态回归模型

若使用滞后算子将式（8）简化为式（10），则得到风电功率预测的ARIMA动态回归模型为式中：B为滞后算子且有BΔPt=ΔPt-1；p、d、q均为ARIMA模型的阶数。式（9）与2.1节中的静态回归模型类似，但其残差项ΔPt不再具有白噪声假设，而是将该残差用式（10）所表示的ARIMA模型代替。

若阶数p、d、q取不同数值，该模型又可分为AR、MA、ARMA 和ARIMA 4 种不同的动态回归模型。通过绘制Δ的自相关（autocorrelation function，ACF）图与偏自相关（partial autocorrelation function，PACF）图，观察拖尾、截尾特性可以初步判断ARIMA 模型的p、q阶数，使用最小化信息准则或交叉验证等方法可以进一步确定p、q的最优取值。在确定动态回归模型阶数后，可以使用最小二乘法或极大似然估计法对式（10）中的参数进行估计［15］。

2.3 动态谐波回归模型

ARIMA动态回归模型可以刻画风电时间序列的静态回归特性与动态变化特性，但对于具有季节性特点的风电时间序列，该方法仍不能完整刻画其所有规律。文献［18］指出风能受太阳辐射和地球自转影响具有以日为周期的特性，因而风电具有以24 h为周期的日季节性。为了考虑上述日季节性，本文提出基于傅里叶分解的动态谐波回归模型。

傅里叶分解可从频域角度描绘风电功率时间序列的周期特性，对于一切周期性函数，均可以通过傅里叶级数进行逼近。因此在动态回归模型中，加入傅里叶级数项表征风电时间序列的季节性，进而构成动态谐波回归模型来更全面地对风电预测进行建模。用于风电超短期预测的ARIMA 动态谐波回归模型为

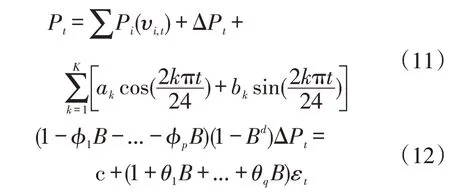
式中：k为傅里叶级数次数，该值可通过观察时间序列的频域特性进行初步判断，然后使用交叉验证确定最终次数；K为傅里叶级数的最高次数。

3 算例测试与分析

3.1 实验设计

本文选取一号风电场数据进行超短期风电功率的预测，预测提前期为h=4 ，使用均方根误差（root mean squared error，RMSE）、可决系数R2对预测精度进行评价，其中RMSE为负向指标，R2为正向指标。

数据被划分为训练集（8 760 h）和测试集（744 h），分 别 对 应2012 年1 月1 日 至2012 年12 月30 日 和2012 年12 月31 日至2013 年1 月31 日。训练集中，使用交叉验证进行特征选择和超参数寻优，待选择的特征为不同高度风速υi，待寻优的超参数包括ARIMA 阶数p、d、q以及傅里叶级数项数K。交叉验证以1 008 h（6 周）为窗口长度向前滚动，模型参数由极大似然法估计。测试集用于对确定的预测模型进行预测精度评估。风电功率标幺值的取值范围为［0,1］。因此，若预测功率小于0，则取下限0；若预测功率大于1，则取上限1。

3.2 算例分析

3.2.1 风速特征选择

式（1）将原始数据转化为高度10 m 和100 m 处的风速，因此需要从中选出风电预测的最佳回归子集。潜在的最佳回归子集为{υ10}、{υ100}、{υ10,υ100}。本文使用交叉验证最佳回归子集，评价结果如表1所示。

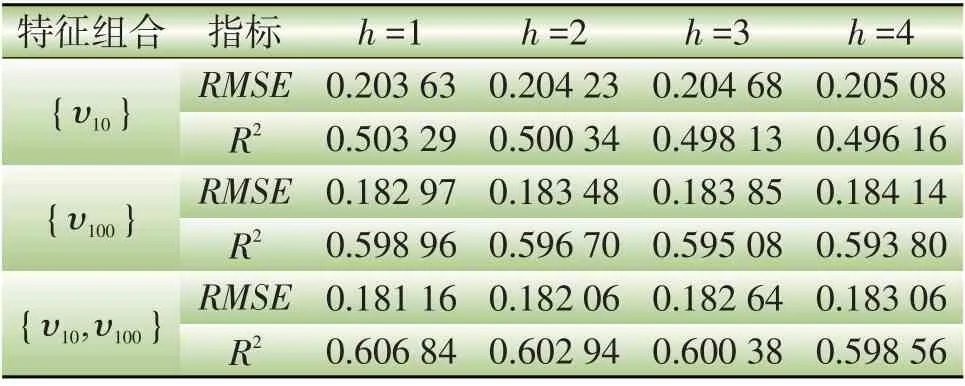
表1 3种预测变量组合的RMSE 和R2 评价结果Table 1 RMSE and R2 results of three combinations of predictors

表1 中h为预测提前期，h=1 表示预测提前为1 h。表1结果显示，无论单步预测，还是多步预测，按照{υ10}、{υ100}、{υ10,υ100}的顺序，RMSE评价结果逐渐变小，R2评价结果逐渐变大，这表明{υ100}具有比{υ10}更高的预测精度，而{υ10}能一定程度上补充预测信息，提高静态回归模型的预测精度。因此，选择{υ10,υ100}作为最佳回归子集能达到更优的预测效果，静态回归模型确定为

式中：β均为待估计参数。

此外，对于相同的特征组合，随着预测提前期的增加，RMSE逐渐变小，R2逐渐变大，评价结果的恶化表征预测效果变差；对于相同的预测提前期，随着RMSE逐渐变小，R2也逐渐变大。可以发现，RMSE与R2具有完全一致的评价效果，因此后文将仅展示RMSE的评价结果。

为判断本小节所确定的静态模型是否能充分描述风电功率出力特性，需要对静态回归残差进行Ljung-Box 检验。给定显著性水平α=0.05，检验结果为0，小于临界值0.004，所以应拒绝原假设。这说明静态回归的残差中仍具有可用信息，有必要使用本文所提模型对残差建模，以提高风电预测精度。

3.2.2 超参数寻优

本文所提预测模型的超参数包括两类，即ARIMA模型超参数p、d、q和傅里叶级数项数K。本文分3阶段确定各超参数值，即依次采用单位根检验确定差分次数d，采用ACF图、PACF图与交叉验证确定阶数p和q，采用交叉验证确定傅里叶级数项数K。

由于ARIMA模型对时间序列具有平稳性要求，因此首先使用KPSS方法对残差进行单位根检验，检查静态回归残差是否具有平稳性。给定显著性水平α=0.05，检验结果为0.110 8，小于临界值0.463 0，应接受原假设，即残差具有平稳性，因此不需要进行差分，即d=0。

为判断ARIMA模型阶数p和q的大致范围，需要对残差的自相关性进行分析，图1 给出了静态回归残差的自相关性图和偏自相关性图。

图1 静态回归残差的自相关性图和偏自相关性图Fig.1 ACF and PACF plots of regression residuals

从图1 中可以看出，静态回归残差仍具有较高的自相关性。自相关性图具有拖尾特点，偏自相关性图具有明显的一阶截尾、轻度的二阶截尾特点，因此可以考虑p=1、2 且q=0，即AR（1）或AR（2）模型。接下来使用交叉验证从以上2种待选模型中进一步确定最优参数。2种模型评价结果如表2所示。

表2 不同阶数AR模型的RMSE 对比Table 2 RMSE comparison of different AR models

表2 结果表明AR（1）与AR（2）预测精度接近，但AR（1）在2～4 h 预测中具有更高的预测精度，而AR（2）只在一步预测中表现更好。因此，可以选择更稳定的AR（1）作为残差模型，即p=1且q=0。

图1的ACF图显示，自相关系数除了随滞后阶数的增大而逐渐减小，还在减小过程中具有上下波动特点，说明静态回归残差中具有一定的季节性，这是由于静态回归中没有考虑风电功率的日季节性特征，因此有必要在模型中增加傅里叶级数。本文将傅里叶级数项数的寻优范围设置为K=1、2、3、4并使用交叉验证确定最佳的项数。结果显示K=2时，模型具有最高预测精度，其4步预测的RMSE结果分别为0.093 14、0.131 37、0.154 28、0.171 18。

3.2.3 模型预测效果

本小节使用测试集对动态谐波回归模型的预测精度评价。为验证预测模型的改进效果，本文同时给出了静态回归模型、动态回归模型的评估结果。

（1）静态回归模型：预测变量为{υ10,υ100}。

（2）动态回归模型：在（1）基础上，采用AR（1）对静态回归残差进行建模。

（3）动态谐波回归模型：在（2）基础上，添加K=2 的傅里叶级数作为新增的预测变量。

图2 展 示 了2012 年12 月31 日至2013 年1 月1日共2 天的超短期滚动预测结果，测试集上的完整评估结果如表3所示。

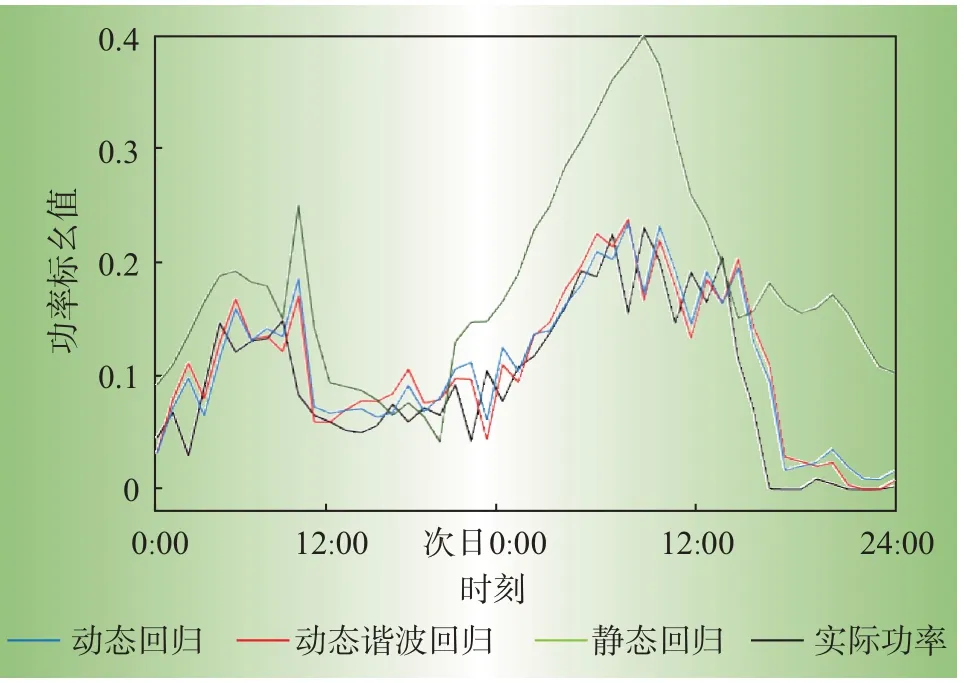
图2 3种回归模型的预测结果Fig.2 Forecasting results of three regression models

表3 3种回归模型的RMSETable 3 RMSE comparison of three regression models

图2 中3 条回归曲线与实际发电功率曲线表明，静态回归模型预测结果与实际风电功率差别很大，而动态回归模型与动态谐波回归模型均具有良好的预测效果。从表3 可以发现，在所测试的预测提前期中，静态回归模型、动态回归模型、动态谐波回归模型的预测精度均依次提高，验证了所提模型的改进效果。

3.3 预测误差分析

为验证动态谐波回归模型的有效性，本小节对180 天每天的RMSE数据统计分析，并选取动态回归模型与ARIMA 模型作为对比，其中AIRMA 阶数为（2,0,0），即AR（2）。图3 为预测提前期h=1 时，3种模型的RMSE 频数分布直方图。表4展示了五数概括法对3种模型预测误差分析的统计结果。

图3 h=1时，3种模型的RMSE 频数分布直方图Fig.3 Frequency distribution histogram of RMSE for the three forecasting models when h=1

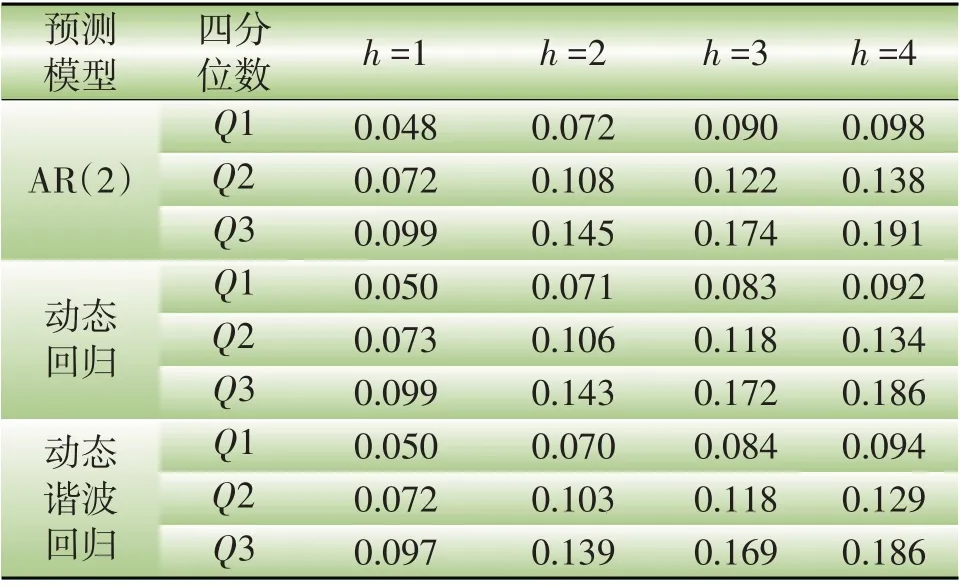
表4 3种预测模型RMSE 分位数Table 4 Quantiles of RMSE for the three forecasting models

图3中，3种模型预测精度分布集中在0.1以内，均具有较好的预测稳定性。表4 中，Q1、Q2、Q3 分别表示第1、第2、第3 四分位数。表4 表明，动态谐波回归的RMSE分布更加集中，动态谐波回归具有更加稳定的预测效果，说明所提模型能够有效地对实际系统进行预测。

3.4 与现有预测模型对比

为验证动态谐波回归模型具有比现有模型更高的预测精度，本文选择了超短期预测中常用的持续法（naive），即以最新观测值作为预测结果和ARIMA 模型作为对照，其中ARIMA 模型为AR（2）。2种模型与所提动态谐波回归模型采用完全相同的测试集和滚动预测方式。图4展示了2天的预测效果，测试集上的完整评价结果如表5所示。

图4 动态谐波回归与现有预测方法的对比Fig.4 Comparison of dynamic harmonic regression and two commonly-used existing approaches

表5 动态谐波回归与现有预测方法的预测精度比较Table 5 Comparison of the prediction accuracy between dynamic harmonic regression and two commonly-used existing approaches

图4 中，3 种模型预测值均与实际功率接近，表明均具有较好的预测效果。从预测精度上分析，动态谐波回归模型预测精度高于其余2种常用预测模型，说明本文所提模型具有一定的现实意义。

4 结论

本文提出动态谐波回归方法进行超短期风电功率预测，并通过某风电场运行数据进行验证，得到以下结论。

（1）静态回归的残差具有高自相关性，采用ARIMA方法对残差建模可以显著提高超短期预测精度；

（2）风电功率具有日季节特性，傅里叶级数可以有效地描述该特点；

（3）本文所提动态谐波回归方法预测精度高于现有的常用预测方法。D