考虑电动汽车需求响应的微电网预测控制研究

史倩芸，吴传申，高 山

（1.东南大学 电气工程学院，南京 210096；2.江苏省智能电网技术与装备重点实验室，南京 210096）

0 引言

清洁能源正逐步取代污染严重的化石燃料，成为当今世界重要能源之一。电动汽车（electric vehicle，EV）因其使用清洁能源、没有排放污染的特点而被各国广泛推崇，电动汽车行业逐步兴起。

当EV 数量较少时，其对电网的影响较小，不会引起电网较大的波动，但随着EV的广泛应用，大规模集群EV接入电网可能对电网的运行管理产生负面影响［1］。大量无序充电模式的EV 接入电网会增加或产生新的峰值负荷，对分布式电网［2］造成巨大的挑战，比如在用电高峰时段造成电网变压器的容量超载，导致其过热、过载，跳闸甚至大面积停电，危及电网的安全稳定运行［3—4］。

因此，为了减轻电网的压力、有效地将清洁能源引入微电网并最大限度地发挥作用，需要对集群EV 进行有效的充放电管理［5］。集群EV 不仅是负荷，还是一种有效的储能设备，既可以从电网获取电能，也可以向电网输送电能。通过车辆到电网（vehicle-to-grid，V2G）的技术可以实现在电网负荷峰值时EV 放电、谷值时EV 充电，从而对电网负荷曲线进行削峰填谷，减轻电网的负荷压力。

在预测策略方面，文献［6］通过对集群EV到达时刻及剩余电量的多重不确定性采样，得到各时间段EV的到达数量及剩余电量的预测值，并以此预测值为基础，对电动汽车充放电功率进行优化求解。文献［7］提出了一种基于场景概率的方法，对配电系统进行典型日内的概率潮流分析，采用K-means聚类给出充电负荷和光伏出力的概率场景集，以此作为预测值进行潮流分析。文献［8］提出接入充电站开始充电的时刻以及当日行驶的距离是影响EV充电负荷的两个因素，并根据这两个因素的概率分布，建立了一日一充的模式下，单辆和集群EV充电负荷的统计学模型。

目前已有许多学者对电动汽车的需求响应进行了研究分析，通过控制电动汽车各时段的充放电功率，实现最小化电网与微电网之间进行功率传输的目标。双层优化控制策略研究方面，文献［9］通过双层最优充电策略对优化问题的求解，保持了电网变压器供电负荷曲线波动最小，并实现了每个电动汽车用户的充电成本最小的目标；文献［10］也提出一种双层优化策略，上层通过网损最小确定充电位置、下层通过充电费用最小确定充电时间的有序充电模型，结果显示该方法能有效地减小网损、平抑波动。文献［11］通过对双层优化控制策略进一步改进，提出了基于动态规划的双层优化策略，上层使用动态规划方法进行求解，下层选择各EV 的充电方案，确定最好的充电模式；文献［12］在双层模型的基础上构建了电动汽车3 层能量管理模型，并通过紧耦合和松耦合两种模式，有效地进行负荷削峰填谷及新能源的消纳。

以上各研究通过对集群电动汽车的充放电控制，虽然在一定程度上实现了微电网中负荷的削峰填谷，从而降低了电网运行的成本，但在上层优化时都没有计及下层单个EV的实际需求，即未考虑单个EV的充电紧迫性，可能存在离开充电桩时某些EV电量仍过低的现象。

为了弥补现有充电策略的不足，本文根据不确定性采样结果建立一个双层模型预测控制策略对接入微电网的电动汽车进行最优充放电管理，并在上层集群优化时考虑下层单个EV的充电紧迫性，对各EV进行调控，从而最大程度满足各电动汽车的充电需求。

1 微电网模型

1.1 系统结构

本研究在包含风电、基本负荷以及集群电动汽车的微电网系统中进行，微电网与电网之间通过传输线进行连接，系统结构如图1所示。

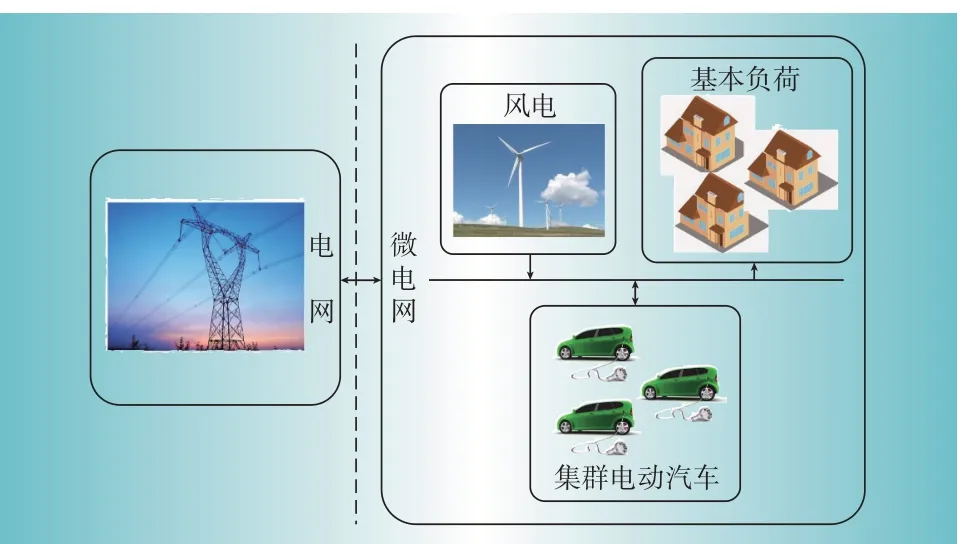
图1 微电网系统结构及其与电网互联示意Fig.1 Schematic of the microgrid system structure and its interconnection with the grid

由图1 可以看出，微电网与电网之间的能量可以通过传输线进行传递。微电网内部，风电向电网供电，基本家用负荷从电网中获取电能，而集群电动汽车既可通过充电从电网获取电能，也可通过放电向电网输送电能。因此微电网与电网之间的能量传输可以通过集群电动汽车的充放电与风电、基本负荷的协调进行最小化控制。

由于本文主要研究某小区这一微电网中集群电动汽车的充放电控制策略，此处的集群电动汽车在居民结束工作返回家中后开始充电，因此本文假设充电周期为18:00—次日6:00，将此周期平均分成72个时段，每时段为10 min［13］。为了使研究符合实际情况，需要对初始各EV 的荷电状态（state of charge，SOC）及到达时刻进行合理预测。

1.2 集群电动汽车模型

各电动汽车开始充电的时间及其当日的行驶距离满足一定的概率分布。可以认为，电动汽车开始充电的时间满足一种对数正态分布［14］，其概率密度函数为

式中：μ1为均值；σ1为方差；t0为时间的偏移量。

各电动汽车当日的行驶距离也满足一种对数正态分布，其概率密度函数为

式中：μ2为均值；σ2为方差。

由于各电动汽车刚接入微电网时的电量与其当日的行驶距离有关，因此各EV 的初始电量可以表示为行驶距离d的函数

式中：CEV为各电动汽车蓄电池的标称容量；P0为各电动汽车行驶1 km消耗的电能。

根据实际情况，假设所有电动汽车基本于次日2:00前到达，并且各EV到达充电站时的SOC均大于0。

本文对集群电动汽车充放电策略进行研究时，考虑了某些电动汽车充电的紧迫性，因此在集群EV参与微电网内功率调控时，需去除该部分电动汽车，并将其充电功率进行单独计算，最终与参与调控部分电动汽车充放电功率相加，得到整体集群EV各时段的充放电功率。

2 微电网预测控制策略

2.1 滚动优化控制策略

滚动优化与传统的全局优化不同，前者在每一时刻优化性能指标只涉及到从该时刻起的未来有限的时间，而到下一时刻，这一优化时间同时向前推移，不断地进行在线优化。这种滚动优化虽然无法一次得到理想的全局最优解，但是反复对每一采样时刻的偏差进行优化计算，可及时校正控制过程中出现的各种复杂情况，从而更加准确地预测控制集群EV的充放电功率。

2.2 双层模型预测控制策略

首先，对电动汽车的到达时间及剩余电量进行不确定性采样，并对风能和基本负荷进行预测。其次，通过上层优化获得参与调控的集群电动汽车的整体充放电功率。接着进行下层优化控制，将充放电功率分配给参与调控的各个电动汽车，并使其满足一定的约束条件。最后，集群电动汽车的特性被反馈到上层。优化过程一直持续到最后一个时域结束。双层优化过程如图2所示。

图2 微电网双层优化流程Fig.2 Double-layer optimization process of microgrid

2.2.1 上层优化模型

（1）目标函数

为使得电网与微电网之间的传输功率为最小值，上层目标函数可以表示为

式中：Pi为参与调控的集群EV 在第i时段的充电功率；Ci为第i时段风能与基本负荷的差值；P为不参与调控的EV集群在第i时段的充电功率；H为时段的个数，取为72。

（2）判别方法

首先需要判别各EV 是否参与调控，判别方法如下。

假设各EV自其接入微电网后均以额定功率Prat进行充电，计算H时段初各EV的SOC值，可表示为

其中

式中：为额定功率充电时第k辆EV在i时段初的SOC值，i=1,2,…,H-1，k=1,2,…,N；Prat为EV 的额定功率；h为时间区间的长度；ηc和ηd分别为EV的充电和放电效率。

若0.9，表示EV以额定功率充电时，在最后一段滚动时域充电后，EV 的SOC仍小于0.9，说明第k辆EV有较高的充电紧迫性，因此不参与调控，始终以额定功率充电。若≥0.9，则参与调控。

（3）约束条件

集群EV的充电功率约束可表示为

式中：Ni为i时段已到达且参与调控的EV数量。参与调控的集群EV的SOC上、下限约束可表示为

式中：SOCi为i时段前到达且参与调控的集群EV的SOC值。

集群EV的SOC随时间的递推式可以表示为

2.2.2 下层优化模型

（1）目标函数

下层目标函数为使得下层各EV 的充放电功率之和与上层优化结果有着最大的匹配度，该目标函数可以表示为

（2）约束条件

各EV的充电功率约束可以表示为

式中：N为该微电网内所有参与调控的EV数量。

滚动时域最后一个时段前各EV 的SOC上、下限约束可表示为

滚动时域最后一个时段各EV 的SOC上、下限约束可表示为

微电网内各EV的SOC随时间的递推式可以表示为

在下层约束中，各EV 充放电功率的分配情况由其充电后的剩余电量来决定，具体的充放电原则为：当集群EV 处于充电状态时，电量低的EV 优先充电；当集群EV 处于放电状态时，电量高的EV 优先放电。

2.2.3 双层模型间的联系

上层模型只是对集群EV 这一整体进行优化分析，只约束了集群EV整体的充放电功率及SOC，并未对单个EV 设置对应的约束条件，因此需要用下层模型来约束各EV的充放电功率及SOC。通过下层优化模型对上层优化后的结果进行修正，即通过反馈修正集群EV的状态，并进入下一滚动时域。

2.3 双层预测控制模型求解

首先考虑集群EV 的约束条件，使用MATLAB中的CPLEX 求解器对以电网与微电网之间的传输功率最小为目标的上层模型进行优化求解。再将上层优化所得结果输入下层模型，在下层模型中将集群充放电功率分为4 类：充电上限、放电上限、充电非上限与放电非上限。考虑单个EV 的约束条件，以“充电时低电量EV优先，放电时高电量EV优先”为原则，对各时刻的充放电功率进行分配。通过滚动优化，对下一时域的集群充放电功率进行更新，直至最后一个滚动时域，最终得到各时段集群电动汽车的最优充放电功率。

3 算例分析

3.1 系统配置及参数

本研究针对某小区的微电网，其中包括3 MW的风机，小区的基本负荷以及300辆电动汽车。

仿真需要用到的各EV参数如表1所示。

表1 仿真中各EV参数设置Table 1 EV parameters setting in simulation

根据当地的风电数据及某电网公司统计的该小区的基本负荷数据，选取某日18:00至次日6:00的数据绘制如图3所示曲线。

图3 风能与基本负荷功率曲线Fig.3 Wind energy and base load power curves

根据不确定性采样得到的结果，绘制出各时段到达的EV数量如图4所示。

图4 各时段到达的EV数量采样结果Fig.4 Sampling result of the total number of EV arrivals at different times

由图4 可以看出，大部分EV 于次日0:00 前到达，且几乎所有EV都于次日2:00前到达充电站，符合实际情况。

3.2 仿真结果分析

本研究将对比电动汽车无序充电、传统优化及考虑充电紧迫性的优化这3种策略。图5展示了风能与基本负荷的差值曲线，以及集群电动汽车无序充电的功率曲线。

图5 风能与基本负荷的差值曲线及无序充电的功率曲线对比Fig.5 Comparison of the difference between wind energy curve and base load and the power of dumb charging curve

无序充电即当EV 刚接入微电网时便开始以额定功率充电，直到充满为止。在22:00前充电功率呈上升的趋势，在其后不断下降，并于次日2:00后几乎降为0。由图5可以看出，两条曲线的变化趋势完全不同。当风能与基本负荷所需电能的差值不断减小时，集群EV的充电功率仍在增加，此时为了满足EV的充电需求，微电网从电网吸收的电能有所增加；当风能大于基本负荷所需电能且其差值不断增加时，集群EV的充电功率却呈现下降趋势且接近0，从而导致风能无法被消纳。图5中，次日2:00后风能远小于基本负荷所需能量，但此时集群EV并未出现放电状态，导致无法用EV 的电能弥补基本负荷所需能量。由以上分析可知，无序充电是一种效果较差的充放电策略，因此需要对其进行优化改进。

图6对比了传统优化策略及考虑EV充电紧迫性的优化策略，功率为正表示集群EV从微电网内吸收电能，功率为负表示集群EV向微电网输送电能。从图6 可以看出，在18:00—20:40 以及21:30—22:00 这两个时间段内，集群EV 的充电功率受到最大充电功率的约束，如式（6）所示，因此它们在传统优化策略及考虑充电紧迫性的优化策略后得到的值相等。在20:40—21:30以及22:00—次日6:00 时间段，集群EV 在考虑充电紧迫性的优化策略下得到的充电功率总是高于传统优化策略下的充电功率，通过上层目标函数的计算可以得到两目标函数的差值为4.064 73 MW2。从图6 还可以看出这两条曲线和风能与基本负荷之差曲线在20:40 后几乎平行，这是由于为了满足上层优化时微电网和电网之间的传输功率最小的目标，且需满足集群EV 的充电功率及SOC约束，只需将EV 所需总能量平铺于整个时域即可。

图6 考虑充电紧迫性前后的优化曲线对比Fig.6 Comparison of optimization curves before and after considering the urgency of charging

将考虑充电紧迫性的优化策略曲线分解为不参与调控EV 的充电功率曲线和参与调控EV 的充电功率曲线，并与传统优化策略曲线进行对比，如图7所示。

图7 两类EV的充电功率曲线与传统优化策略曲线对比Fig.7 Comparison of the charging power curve of the two types of EVs and the curve of the traditional optimization strategy

由图7可以看出，参与调控EV的曲线在18:00—20:20与传统优化曲线重合，这是由于受到了已到达EV的数量约束。在20:20—次日0:30略高于传统优化策略曲线，这是由于参与调控的数量减少使得前期集群EV可以吸收更多的电能用以尽快满足电量要求，从而为后期的放电创造条件。在次日2:00—次日6:00几乎平行且略低于传统优化策略曲线，这是由于在次日0:00 后共11 辆EV 无法参与调控，此时上层目标函数如式（4）所示，需要减去不参与调控的EV的充电功率，即额定功率，因此参与调控的集群EV充电功率曲线略低于传统优化策略曲线。

将不参与调控的集群EV 充电功率曲线与参与调控的集群EV 充电功率曲线进行叠加，即为考虑充电紧迫性的优化策略曲线，如图6 所示。由于不参与调控的EV自其接入微电网后即以额定功率进行充电，因此加上这一部分充电功率后，考虑充电紧迫性的优化策略曲线应高于传统优化策略曲线。

图8 为各EV 在不同时刻的SOC曲线，集群EV的SOC变化趋势与其充放电功率有关，当其充电功率较大时，SOC曲线斜率也较大，相反，当其充电功率较小时，SOC曲线斜率也较小。

图8 各EV的SOC曲线Fig.8 SOC curves of each EV

图8 中EV1、EV2及EV3为参与调控的EV，分别于19:00、20:30、22:00 左右开始充电。其SOC曲线与集群EV的SOC曲线趋势基本相同，由于次日1:00前风能与负荷之差基本大于0，因此此时的充电功率较高，SOC曲线的斜率较大；1:00 后风能与负荷之差小于0，根据优化策略可以供给更多的充电功率，因此SOC曲线的斜率减小，甚至出现放电现象，斜率小于0。充电完毕后各EV 的SOC值稳定在0.9附近。

图8中EV4为不参与调控的EV，因此其SOC自其接入微电网后由于始终按额定功率充电，斜率始终不变，充电完毕后的SOC值约在0.8左右，略低于参与调控的EV的SOC值。

由以上仿真及分析可以发现，本研究所提出的考虑充电紧迫性的优化策略，其充电功率曲线略微差于传统优化策略时的充电功率曲线，但两种策略得到的微电网与电网之间的交互功率相差较小，目标函数差值仅为4.064 73 MW2，相较于传统方法优化目标结果占比仅为4.04%。本文所提出的新策略却充分考虑了实际情况下某些EV 急需充电，更加符合实际，且满足居民的充电需求，利大于弊。

4 结束语

本文提出了一种考虑充电紧迫性的双层优化策略，用以解决某小区微电网中的集群电动汽车充电问题，其中上层对集群充放电功率进行优化求解，下层进行各EV充放电功率的分配，通过两层间的交互形成最优充放电策略。该策略与传统优化策略相比，两网的交互功功率相差极小，但充分考虑到部分EV电量过低急需充电因而不参与调控的情形，最大程度满足了该类用户的需求，使得急需充电的EV始终供以额定功率。这一策略的提出既极大程度提高了电网运行的经济性，又充分满足了用户的充电需求，在集群电动汽车充放电管理上具有更好的表现，更加贴近现实情况。D