基于深度信念网络的日前电价预测

郭 晨，李雪瑞，韩照洋，付学谦

（中国农业大学 信息与电气工程学院，北京 100083）

0 引言

近年来，电力市场建设取得重大进展。电价是电力市场的重要因素，可以确保市场的稳定运行，对电价的预测也逐渐成为学者们关注的焦点。电价是电力市场的关键影响因素，每个参与者都基于电价进行电力交易。因此，提高电价预测的精度对于电力市场中每个参与者而言都十分重要。因此，亟需对电价预测问题开展进一步的研究。

当下国内外电价预测方法有很多，具体归类如下。

文献［1］提出在现有电价预测模型上，对电价残差序列建立时间序列模型，并采用整合移动平均自回归模型（autoregressive integrated moving average model，ARIMA）降低预测误差。时间序列组合模型简单，通俗易懂，计算速度快，缺点是预测的精度较低。

鉴于时间序列组合模型预测精度不高，一些研究人员开始采用神经网络的的方法进行电价预测。文献［2］提出了一种卷积神经网络的预测模型，进行日前电价预测；文献［3］设计了一种先采用集合经验模态分解（ensemble empirical mode decomposition，EEMD）方法，将历史电价分解后，再使用小波神经网络对电价进行预测的方法；为了提高预测精度，文献［4］设计了一种将小波变换与矢量函数结合起来的新型神经网络模型，来进行电价预测。

有研究提出将以上两种模型结合起来。文献［5］在时间序列的基础上，采用回归神经网络的模型进行电价预测；文献［6］提出基于EEMD，支持向量机（support vector machine，SVM）和自回归滑动平均模型（autoregressive moving average model，ARMA）的组合预测模型，但这些组合模型的精确度仍有待提高。

为进一步提高预测精确度，本文采用深度信念网络（deep belief network，DBN）［7］的预测模型来进行日前电价的预测。电价具有时间序列特征［8］，深度信念网络可以更好地捕捉电价波动的时序特征。将小波变换与DBN组合在一起，小波变换将原始电价信号进行分解，再通过分层预训练为所有参数提供良好的初值，然后通过监督微调过程搜索最优值。相比其他单层神经网络，在相同的数据输入下，本文提出深度信念网络训练过程分层，迭代次数多，预测精确度更高［9］。

1 深度信念网络模型

前文介绍了几种传统的电价预测模型，接下来介绍本文所采用的深度信念网络。DBN 主要应用在特征学习、数据分类和生成数据等方面。DBN主要是使用受限玻尔兹曼机（restricted Boltzmann machine，RBM）作为构建模块的无监督学习子部分，外加一个用于预测的逻辑回归层。

1.1 受限玻尔兹曼机

波尔兹曼机（Boltzmann machine，BM）是神经网络的一种。BM 是两层神经元结构的神经网络，由显元构成的显层（visible layer，VL），主要用于输入需要被训练的数据。由隐元构成的隐层（hidden layer，HL），主要用来检测特征。波尔兹曼机结构图［10］如图1（a）所示。

BM 有很强的特征学习能力，但由于其训练和学习需要较长的时间。为优化其耗时长的缺点，Sejnowski在BM的基础上提出了RBM。

RBM 和BM 的区别是，在RBM 中，同一层的神经元是互不相连的，不同层的神经元是双向完全连接的。这样连接的优点是，每层神经元的个数是互不相关的。RBM同层之间没有连接，可以减少信息传递的过程，因此可以缩短求解的时间。

RBM的信息可以双向流动，相当于增加了训练的迭代次数，保证了预测模型的准确性。这会使预测的精度不会下降太多。RBM结构图［10］如图1（b）所示。

图1 结构图Fig.1 Structure diagram

RBM 通过能量函数体现从显层到隐层的概率分布，给定显元vi、隐元hj、其连接权重wi,j以及vi的偏移量ai、hj的的偏移量bj，其能量函数E(v,h)可以定义为

采用能量函数的方式来定义显层和隐层的概率分布

式中：Z为分布函数的归一化常数。

W表示的是每个隐元与显元间的权重［10］

式中：wi,j为从第i个显元到第j个隐元的权重值；M为显元的个数；N为隐元的个数。

因此，可以推导出每个显元和隐元的条件分布概率［10］

1.2 深度信念网络

深度信念网络是由多个RBM 分层堆叠而成，DBN的训练过程包括预训练和微调两部分。

DBN 训练过程包括分层预训练和微调。分层预训练为所有参数提供初始值，而微调根据网络结构探索最优值。深度信念网络预训练过程见图2［11］。

图2 DBN预训练过程Fig.2 DBN pre-training process

逐层的训练过程如下：①最下次的RBM 采用原始输入数据进行充分训练；②固定第一个RBM的权重和偏移量，将底部RBM 抽取的特征作为顶部RBM 的输入；然后，可以将这两个隐藏层视为一个新的RBM，并以相同的方式进行训练；③第2 个RBM 进行充分训练后，将其堆在第一个RBM的上方，重复这个过程训练以尽可能多的RBM 层；④重复以上3 个步骤任意多次；⑤最后，在最顶层添加一个标准预测因子，即逻辑回归，预测因子的训练称为微调过程，它旨在略微调整整个网络中的参数。

2 DBN的微调过程

2.1 小波分解

原始的电价中含有很多非线性和非平稳的因素，这些因素是导致预测电价精度降低的原因之一。因此，我们需要利用小波变换将历史数据分解为多个频率，以使数据在方差和离群值方面有更好的性能。

小波变换可以采用离散形式以提高效率。小波变换的离散形式如下所示［9］

式中：φ为母波；m、n为决定φ缩放和平移参数的两个整数变量；t为离散时间的指标；T为信号f(t)的长度。

本文采用的是一种基于Mallat的快速离散小波变换的算法。该算法由分解滤波器和重构滤波器组成。因此，基于Mallat 算法的多级分解过程可以将历史电价数据分解为一个近似值（An）和多个细小值（Dn），如图3所示［9］。

图3 多级分解过程Fig.3 Multi-level decomposition process

2.2 基于DBN的分层预训练

传统的神经网络非常容易陷入局部最优的问题。当神经网络为深层网络时，因为需要优化的参数更多，这个问题将会变得更加突出。处理局部最优问题的办法就是尽可能将参数初始化。

DBN 在解决以上问题中有较好的方式。DBN训练过程包括分层预训练和微调。分层预训练为所有参数提供初始值，而微调根据网络结构探索最优值。

每次预先训练一个独立的RBM，就可以得到相关的参数a、b、W。训练前的过程是通过对RBM目标函数进行随机梯度上升来实现的，即P( )v的对数似然。这里，P(v)是可见向量在所有隐藏单元上的概率［11］

因此，目标函数的形式如下

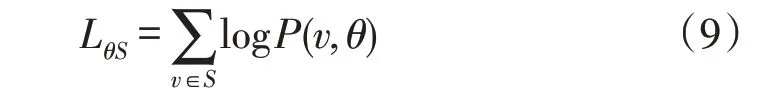
式中：θ∈{a,b,W}和S是训练数据集。

根据贝叶斯统计理论，通过随机梯度上升算法使目标函数（10）最大化，生成稳定且初始状态良好的RBM。梯度上升算法表明，RBM 中的参数a、b、W是根据目标函数L的导数进行更新的，如下所示［9］

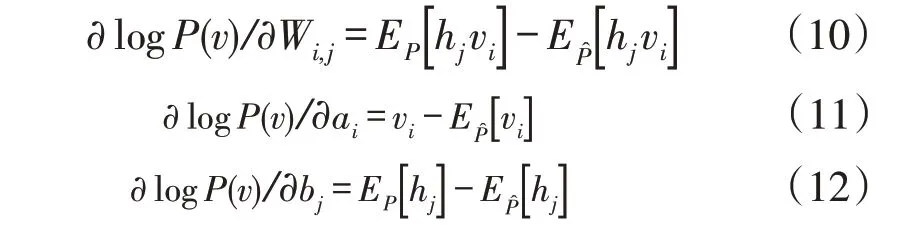
式中：EP、EP^分别为原始数据驱动和重构数据驱动概率。

使用训练数据集上的式（5）和式（6）可以很容易地计算式（10）至式（12）的EP[ ]。然而，式（10）至式（12）中第2 项的计算过程要复杂得多，因为DBN系统学习的是分布P^ 的期望值。一种可行的策略是在可见单元的任何随机状态上应用交替吉布斯采样，直到满足某种收敛准则，如k步。因此，对P^的期望可以通过分析来估计。然而，抽样策略非常耗时，因此很少在现实生活中执行。作为补救措施，提出一种称为对比发散（contrastive divergence，CD）的快速学习方法。该方法采用两种方法来加快采样过程。一种是用训练样本初始化马尔可夫链，另一种是只经过吉布斯采样k步后获取样本，称为CD-k。实验结果表明，即使k=1，CD 也能很好地进行模型识别。

本研究采用CD-1对EP^的期望值进行估计，因此参数a、b、W的更新规则可由式（10）至式（12）推导［9］

式中：上标t为时间步长；η为学习率，在本研究中取0.9。

2.3 监督微调过程

通过研究发现，当RBM 的层数为4 时［12］，预测的精度最高。如2.2 节所述，DBN 中的每层神经元的个数都是基于分层预训练方法进行适当初始化的。这些参数需要在有监督的情况下进行微调，直到DBN的损失函数达到最小值。基于BP算法的有效性，本文采用BP算法来处理这类任务。

在监督微调过程中，BP 算法根据一定的周期，采用自上而下的工作方式。一个工作周期意味着一次性更新所有的参数，这将减少预测的误差。下一步，通过训练集对这些误差进行反向传播，然后将DBN参数重新调整到最优状态。因此，在重复一定的BP周期之后，可以得到最优的DBN参数，这就意味着完成了深度信念网络的训练过程。

3 算例

3.1 实验数据描述

为了验证本文所提出预测模型的优越性，现用美国PJM电力市场真实数据［13］进行仿真预测。其中选 取2018 年10 月1 日 至11 月30 日共61 天历史电价数据预测2018年12月1日的电价，以h为采样周期，将前40天共960 h的样本数据作为训练样本，将后21 天共504 h 的样本数据作为预测集。本文在matlab 仿真平台输入历史电价数据，此数据规模在精度基本达到要求的前提下能够避免仿真过程耗时过长，经过训练得出样本特征，通过504 h的样本集预测得到1 天的电价预测结果，通过与实际电价数据对比验证本文提出模型预测电价的有效性，并通过与EEMD，GA-SVM，ARMA 组合模型、GA-SVM组合模型、ARMA-GARCH 组合模型等组合电价预测模型的预测结果对比说明本文预测模型的精确度。各种模型预测结果见表1。

表1 美国PJM电力市场12月1日各种模型预测结果

3.2 仿真结果

通过在matlab 仿真平台输入历史电价数据，得到美国PJM 电力市场2018 年12 月1 日预测电价的仿真结果如下。

DBN各层神经元个数如表2所示。

表2 DBN各层神经元个数Table 2 Number of neurons in each layer of DBN

本文的预测电价数据与美国PJM 电力市场2018 年12 月1 日的真实电价对比如图4 所示。玻尔兹曼机模型的预测数据与真实电价的对比如图5 所示。

图4 DBN预测的电价与真实电价Fig.4 DBN forecasted electricity price and real electricity price

图5 玻尔兹曼机预测的电价与真实电价Fig.5 The electricity price predicted by the Boltzmann machine and the real electricity price

DBN 预测模型和玻尔兹曼机预测模型的误差对比如表3所示。

表3 DBN预测模型和玻尔兹曼机预测模型的误差对比Table 3 Error comparison between DBN prediction model and Boltzmann machine prediction model

RBM的信息可以双向流动，相当于增加了训练的迭代次数，保证了预测模型的准确性。通过DBN预测模型和BM 预测模型的误差对比，我们可以看出采用DBN预测模型的平均误差比BM预测模型的平均误差更低。因此，采用RBM 预测电价，预测精度并不会下降，反而略有上升。

其他模型的预测数据与真实电价的对比如图6所示。

图6 各预测模型预测电价与真实电价Fig.6 Forecasted electricity price and real electricity price of each prediction model

为进一步说明各个模型的预测效果，将各模型的预测误差放在同一图中进行比较，如图7所示。

图7 各预测模型的误差对比Fig.7 Error comparison of each prediction model

各预测模型的平均误差对比如表4所示。

表4 各预测模型的平均误差对比Table 4 Comparison of the average error of each prediction model

通过图7和表4可以看出，采用DBN进行电价预测，相比单层神经网络的电价预测精确度更高，可以为实际电价预测提供一种有效的方法。

4 结束语

本文提出一种基于深度信念网络的电价预测模型。采用美国PJM电力市场的真实数据进行仿真预测，并与其他神经网络的预测模型进行比较。得出以下结论：本文采用的深度信念网络模型的预测精度更高，使用深度信念网络可以为我国售电公司进行电价预测提供一种有效的方法。D