基于改进卷积深度信念网络的风电机组行星齿轮箱故障诊断方法

钱荣荣，谭 涛

（1.中国航发商用航空发动机有限责任公司，上海 200241；2.南瑞集团（国网电力科学研究院）有限公司，南京 211111）

0 引言

随着新型电力系统的发展，能源结构优化推动源荷变化。随着以风电为代表的新能源接入比例提升，输配电网络的界限将越来越不清晰，负荷侧将涌现多种具备主动响应能力和双向互动能力的新设施，从而使得用户参与系统运行成为可能。风能是当今世界重要能源之一，其消纳一直是政府关注的焦点，而行星齿轮箱是风力发电机的重要装置，由行星轮、齿圈、太阳轮和行星架组成，优点是体积小、质量小以及转矩比高等［1］。一般情况下太阳轮的运动轨迹是绕着本身的中心轴线，以一定的速度进行旋转运动，而行星轮不单自身进行旋转运动，还围绕太阳轮公转，长期运行容易在行星轮、齿圈、太阳轮等处发生磨损和裂纹等故障［2］，如不及时进行处理，将可能导致停机，引发灾难。因此，在电力设备的保护中，研究行星齿轮箱故障诊断具有重要意义。

齿轮箱的故障诊断就是振动信号的识别问题，需对故障信号进行物理建模［3—4］，得到时域和频域信息。针对时频域分析，文献［4］提出了经验模态分解（empirical mode decomposition，EMD），可以处理非线性、非平稳信号，但是该方法容易出现包络不当和模态混叠等问题。针对这种问题，文献［5］提出了变分模态分解（variational mode decomposition，VMD），文献［6］也指出，在故障诊断中VMD比EMD更具优越性。

上面是针对指标进行齿轮箱的故障诊断，但是对于复杂的非线性非平稳信号，诊断效果有限。随着机器学习近几年的迅速发展，基于数据驱动的齿轮箱故障诊断已经得到了越来越广泛的应用。例如，K近邻算法［7］、最小二乘支持向量机［8］和神经网络［9］已在相关领域得到了一定的应用。但是面对复杂的高维数据时，以上方法需要一定的人工经验，识别过程比较麻烦。因此，深度学习得到了应用，文献［10］提出了一维卷积神经网络在齿轮箱故障检测中的应用，一层一层地提取出故障特征，再输入分类器进行故障识别，达到了很好的分类效果。

以上研究可以很好地识别故障，可是也存在着一些问题。其一是卷积神经网络存在权值共享问题，虽然可以提高网络的运行速度，但是面对输入数据过多的情况，会出现训练不多导致精度不高的问题；其二是以上方法中的网络的超参数是根据经验提前给定的，如果选取不当就会出现过拟合和欠拟合的现象。

针对上述问题，本文提出卷积深度信念网络的齿轮箱故障检测方法。首先用VMD 分解对原始信号进行预处理，提取出最能反映故障特征的数据作为网络的输入，利用混沌粒子群算法进行优化，根据适应度函数最小，选取出最优的超参数，提取故障特征，最后经过softmax分类器进行故障分类。

1 卷积深度信念网络

卷积深度信念网络（convolution deep belief network，CDBN）由卷积限制玻尔兹曼机（convolution restricted boltzmann machine，CRBM）一层一层堆叠而成。CRBM由可视层、隐藏层和池化层组成，结构如图1所示。可视层与隐藏层之间通过一个卷积操作，为了防止特征过多，形成过拟合，再加了一层池化层。

图1 CRBM结构Fig.1 Structure of CRBM

可视层与隐藏层之间的能量函数为

式中：θ为{wk,b,c}；wk为卷积核参数；b、c分别为可视层、隐藏层的偏置；v、h分别为可见单元、隐藏单元的值。

隐藏单元的条件概率为

可视层的条件概率为

式中：s为sigmod函数。池化层一般采用最大概率池化。CDBN由多个CRBM堆栈而成，结构如图2所示。其中，每一层的可视层由上一层的输出隐藏层连接。

图2 CDBN结构Fig.2 Structure of CDBN

网络前馈计算过程，利用逐层贪婪算法，每层利用对比散度法进行训练，参数更新公式如下

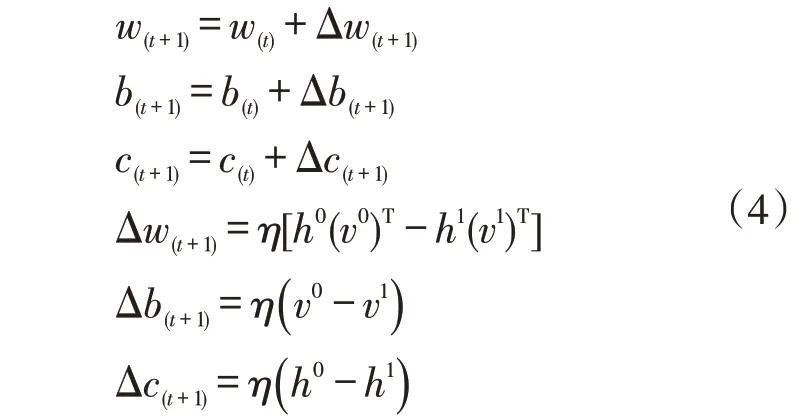
式中：η为学习率；t为迭代次数；v1和h1分别用对比散度法，一次抽样得到。

2 粒子群优化算法

2.1 算法原理

粒子群算法（particle swarm optimization，PSO）最初是根据鸟群的运动设计出来的，每个鸟作为一个粒子，可以用两个量来表示属性，即速度v和位移x。其中速度代表粒子搜寻的快慢，位移代表粒子搜寻的方向。

若我们设定目标函数为f(·)，粒子总数为N，则和gbest满足如下公式

2.2 混沌映射

粒子初始位置的选择对全局的搜索有较大的影响，本文引用混沌变量对粒子进行初始化。映射的混沌变量公式如下

式中：μ为分叉参数，0＜μ ＜1。因此，初始化种群可以表示为

式中：D为混沌变量的维数；m为粒子数；为粒子i的j维分量。

将映射到对应的xij中，可得

式中：xmax,j、xmin,j分别为粒子的j维分量的上、下限。

同理，初始速度vi也可由上述初始化种群生成，故最终得到粒子i的初始化位置xi=[xi1,xi2,…,xiD]和初始化速度vi=[vi1,vi2,…,viD]。

3 诊断流程

基于卷积深度信念网络的故障诊断过程如图3所示。

图3 行星齿轮箱故障诊断方法流程Fig.3 Fault diagnosis process of planetary gear box

选取原始信号作为输入与可视层直接相连，每个数据维度为1，故可视层通道数为1，卷积核的高度为1，卷积核的深度与下一层通道数相同，卷积核的宽度可以决定输入信号特征信息，故其值的选择很重要。此外，池化因子、迭代次数和学习率都对网络的训练有影响，当隐藏层的层数为2时，将上述参数组成一个8维的混沌相量，粒子i的参数包括卷积核的宽度、池化因子、卷积核的深度、学习率、训练批大小等。

其中，卷积核的宽度、深度、池化因子和训练大小应该是整数，这些参数在每次更新的过程中按照四舍五入取整。

将训练集的输出误差作为适应度函数，即

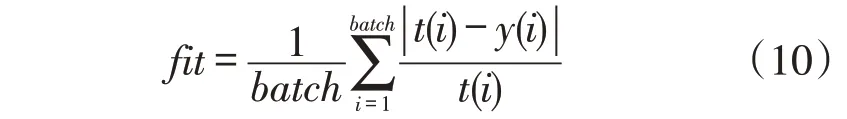
式中：t(i)为实际输出值；y(i)为理想输出值；batch为数据输入的样本个数。

基于粒子群算法的卷积深度信念网络的行星齿轮箱故障检测训练过程如下：①对原始信号进行VMD 分解，利用峭度准则构成4×2 400 维输入信号。②设置PSO基本参数，即种群规模以及最大迭代次数，并将表中的参数作为PSO算法的粒子分量，用混沌变量初始化参数。③根据粒子确定CDBN的结构，将①中的训练集的输入特征值输入到CDBN 中，并将训练误差fit作为适应度函数值，确定pbest、gbest。④如果gbest的适应度值小于给定阈值或者达到最大迭代次数，那么停止迭代；否则，利用位置x和速度v的更新公式来更新粒子，返回步骤③。⑤根据最终的gbest确定CDBN 的结构以及CDBN 的参数值，形成性能较好的CDBN。⑥通过测试集来验证CDBN 行星齿轮箱故障检测的有效性。

PSO算法的训练流程如图4所示。

图4 行星齿轮箱故障诊断方法流程Fig.4 Fault diagnosis process of planetary gear box

4 实验

4.1 实验说明

行星轮被安装在齿轮箱内，在齿轮箱的壳上安装传感器来采集振动信号，具体实验台如图5所示，图5 中6 个数字从小到大分别代表驱动电机、转速控制系统、保护壳、行星齿轮箱、平行齿轮箱和负载。

图5 齿轮箱故障模拟实验平台Fig.5 Failure simulating platform of gear box

本文主要研究的是行星齿轮箱，其内部结构图如图6所示，包含行星轮、行星架和太阳轮。其中行星架和太阳轮一般不易损坏，而行星轮寿命则相对短，我们选取一级行星轮为故障试验行星轮，具体故障包含磨损、点蚀和断齿。行星轮中齿轮磨损的主要原因有过载或润滑剂不足，齿轮点蚀的主要原因有齿面硬度低、载荷不均，齿轮断齿的主要原因有齿轮瞬间冲击过大或齿轮过载。

图6 齿轮箱内部结构Fig.6 Internal structure of gear box

4.2 定速齿轮实验

4.2.1 数据采集

设置电机转速为1 800 rpm，采样率为12 kHz。对各种状态进行采集，得到原始信号。以断齿为例，对其进行VMD 分解，得出本征模态函数如图7所示。

图7 VMD分解的前6个本征模态函数Fig.7 The first six eigenmode functions of VMD decomposition

为了使样本数据至少包含一次冲击，选取输入信号的数据点个数为2 400，对每个本征模态函数求取峭度，选择峭度最大的4 个本征模态函数按照从大到小构成通道数为4 的1×2 400 维特征输入相量。

4.2.2 种群规模的选择

种群规模的选择对实验结果会产生一定的影响。选取隐藏层的个数为2，迭代次数为200，每种状态下选择100 个样本作为训练，25 个样本作为测试。根据3节的方法，选择最优的网络结构，最终的准确率和种群的关系如图8 所示。如图8 所示，当PSO算法的种群规模为20时，训练集与测试集的准确率都较低，而当种群规模达到60 时，训练集与测试集的准确率都较高，且测试集的准确率为最高。

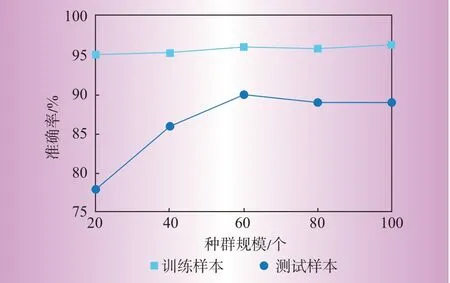
图8 不同种群规模下的准确率Fig.8 Accuracy under different population sizes

4.2.3 隐藏层层数的选择

隐藏层的层数对试验结果也有影响，层数选择过大，不仅加大运算时间，而且会造成过拟合，影响识别的准确率；层数选择过小，无法将特征相量深层学习，不能很好地提取故障特征，精度达不到要求。故选取种群规模为60，迭代次数为200，每种状态下选择100个样本作为训练，25个样本作为测试，最终隐藏层的层数与准确率的关系如图9所示。在隐藏层为3层时，准确率达到最高95%，再增加隐藏层层数并不会增高准确率反而可能会降低准确率，在隐藏层数达到第七层时准确率甚至下降到了93%，所以最终我们选定隐藏层为3层。

图9 准确率与隐藏层层数的关系Fig.9 The relationship between the accuracy and the number of hidden layers

4.2.4 CDBN网络结构的参数

当隐藏层为3 层时，构成新的粒子参数，按照3节的方法构成新的粒子，是在2 层隐藏层的粒子基础上多了卷积核3 的宽度、深度以及第三个池化因子。用训练集训练粒子群优化算法下的深度信念网络，得到最小适应度函数的粒子参数如表1。

表1 粒子的参数值Table 1 Parameter values for particles

因此，CDBN网络的结构根据上表已经确定，并将其与卷积神经网络和不进行粒子群算法优化的CDBN 网络进行对比，得到迭代次数与测试误差关系如图10所示。当迭代次数达到500时，网络的误差达到稳定状态，因此，后面的训练中，将迭代次数设置为500。

图10 不同迭代次数下的测试误差Fig.10 Test error under different iterations

对每层的输出进行主成分分析，归一化后的二维离散点如图11所示。从左到右分别为第一层、第二层和第三层的二维可视化散点图。从图11可得，第一层到第三层中，不同的故障类型开始分散，到第三层时，起到了一定的可分性。

图11 每层的特征可视化Fig.11 Feature visualization of each layer

4.2.5 健康诊断

随机选取每种状态下的200 个样本，共800 个样本进行训练。剩下每种状态下100 个，共400 个样本进行测试，为了防止试验的偶然性，共进行了10组试验，诊断的结果如表2所示。在10次实验中PSO+CDBN 的方法准确率一直是3 种方法中最高的，有4次实验甚至能达到100%，其余6组实验也都在99%以上，而单独使用CDBN 和PSO+DCNN 的效果并不太理想。

表2 各种方法10次试验结果Table 2 Results of 10 tests with various methods

每种健康状态的准确率如图12 所示。如图12所示，PSO+CDBN 的方法对于4 种不同的齿轮磨损状态的检测正确率非常高，而其他两种方法对于4种不同的齿轮磨损状态的检测正确率没有PSO+CDBN方法高，且对于断齿状态下的检测准确率较低。

图12 不同健康状态的准确率Fig.12 Accuracy of different health states

4.3 变速齿轮验证

前文是电机恒定转速情况下的实验，为了验证本文提出的方法的普适性，将前文网络应用于变速齿轮箱中，改变负载大小，将电动机的转速从1 800 rpm开始升高，加速4 s。根据电拖知识可得，电动机加速时，转速大小变化为：n=1800-a0(1-e-t/τ)，其中，a0为大于0的系数，τ为时间常数，实际值根据电动机的参数确定，测得的转速随时间的变化如图13所示。

图13 转速变化曲线Fig.13 Changing curve of rotation speed

诊断过程同定速齿轮，并将其与DCNN 和不进行混沌粒子群优化的CDBN进行对比。进行10次实验，得到的准确率如表3所示，不同状态的准确率如图14所示。由此可得，在变速情况下，混沌粒子群优化的CDBN网络仍然具有较好的故障识别效果。

图14 不同健康状态的准确率Fig.14 Accuracy of different health states

表3 各种方法10次试验结果Table 3 Results of 10 tests with various methods

5 结束语

本文针对振动信号通常是非平稳并噪声污染严重的问题，提出一种混沌粒子群算法的卷积深度信念网络的故障诊断方法，自动优化网络的超参数，可以避免过拟合和欠拟合的现象。通过定转速和变转速的实验数据测试，所提出的故障诊断方法能达到较高的准确性，优于卷积神经网络和不进行超参数优化的信号的分类。为风电消纳提供了良好的基础，为未来风电参与需求侧响应提供了有利保障。D