铝合金板料多道次成形极限预测研究

0 引 言

随着新能源汽车行业的发展，对轻量化车身的成形质量提出了更高的要求。使用计算机辅助工程（computer aided engineering，CAE）技术依据板料成形极限能有效预测车身覆盖件首次塑性变形过程中的各种缺陷。在以铝合金代替低碳钢实现轻量化的趋势下，新牌号铝合金板料的多道次成形极限预测已成为研究热点。

上世纪60年代以前，薄板成形后是否存在缺陷没有可靠的预测方法。由大型模具冲压成形的车身覆盖件常出现缩颈、起皱和开裂等缺陷，修模工作耗时长。由S KEELER

和G GOODWIN

开发的成形极限图（forming limit diagram，FLD）可表征材料发生塑性变形后的成形极限，成形极限图中的成形极限曲线（forming limit curve，FLC）形状和位置定义了材料是否发生破裂的边界。FLD在有限元分析、模具型面优化、生产试模和生产过程中的质量控制等方面发挥了重大作用。

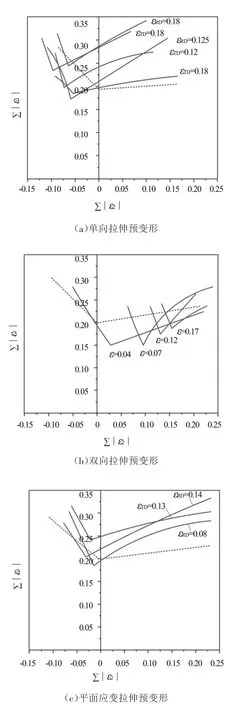
FLD的局限性为只在加载路径是线性的过程中有效，即在整个成形过程中，塑性应变的比率是恒定的。图1所示为A GRAF等

对2008 T4铝合金进行不同预变形后绘制的FLC（曲线1～12），即双线性应变路径下的FLC，可见成形极限曲线在预应变条件下表现较强的应变路径相关性。

应变路径效应降低了ε-FLD在二次成形结果预测的准确性，特别在多道次成形中，应变路径复杂多变，同时叠加轧板的各向异性，更增加了成形极限预测的难度，因此依赖应变路径的FLD已不满足板料多道次成形效果预测的要求，需要研发一种在预变形后仍然可以较准确地预测后续成形极限的非路径依赖的准则。

企业的内部审计部门对审计人员的专业知识有着很大的专业要求，但是我国很多审计专业人员都是从财务方面的人员转型而来，这就使得他们对于审计的专业知识掌握并不多，导致所做的审计报表也并不严格，对审计问题的处理能力较差。企业的科技创新需要审计部门做好一系列的报表、评估文件以及各类预算、国家政策等。若审计人员对审计知识的掌握不高，必定会导致决策实施时出现各种问题，使得决策出现错误的结果。其次，企业也缺乏对审计人员的资格认证[3]，以及对于他们的专业培训，使得一些新上任的审计人员对于企业独特的审计要求掌握并不完善，无法快速的将审计知识运用于审计工作中，这对于企业的创新发展也有一定程度的影响。

以下分析了国内外多种复杂加载条件下的成形极限预测模型，并以铝合金为研究对象讨论了预变形加载问题，探究如何获得单向和双向均匀预应变场，为后续研究二次加载下铝合金薄板成形极限预测提供前期准备。

1 预变形对成形极限图的影响

除了轻量化材料的各向异性，在板料成形过程中受复杂应力场作用，特别是在多道次成形中，板料的应变路径通常是非线性的，研究在复杂应变路径下板料的成形极限是提高板料成形结果预测的一大难题。为了探究应变路径对成形极限的影响，国内外学者做了大量试验和理论研究。

让我意料不到的是老陈居然打电话举报我。那是在我那个朋友来过之后的第二天，两个警察敲响了我的门。听到敲门声，我还以为是老陈呢。谁想开门后却发现站在门外的是两个警察。只是出乎意外的是其中的一个警察我认识，他也喜欢逛古玩市场。见开门的是我，警察小徐说，怎么是你？

通常铝合金板料需经多道次冲压成形才可成为车身覆盖件。为了方便研究，将第一道次成形定义为预变形，重点观察第二道次及后续道次塑性变形的应变极限曲线与原板料的塑性成形极限的区别，进而研究预变形的应变路径对成形极限曲线的影响。

从微观角度看，预变形对铝合金具有冷作硬化效应，促进强化相析出，使基体中沉淀相更均匀分布，减少晶界上不连续的粗大沉淀相数量，提高力学性能。随着预变形量的增加，试样的沉淀密度降低，这是因为大变形量使试样积累更多位错，促进了时效析出，峰值时效时间提前，缩短了时效时间，使析出相稀疏且尺寸粗大不均匀

。

1.1 获得均匀预应变的试验方法

1.1.1 双向拉伸预变形

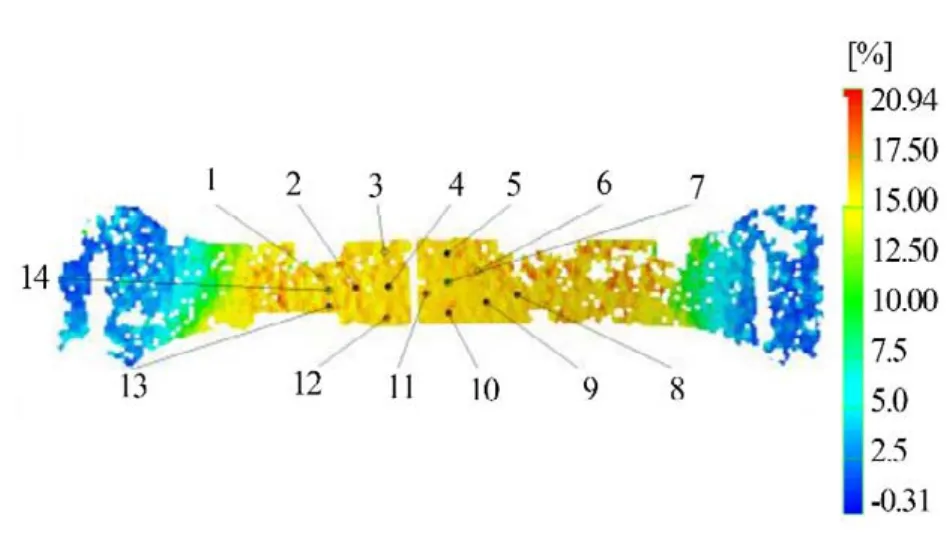
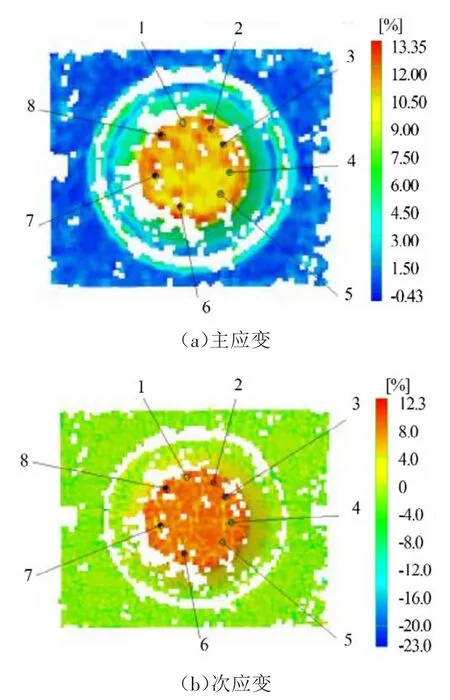
不同应变模式下试样的预变形结果采用Argus应变测量系统获得。该系统由高精度摄像仪器、计算机软件系统以及编码点组成，如图6所示。应变场扫描云图如图7、图8所示，选取各标记点应变值如表1、表2所示。

(3) 物面边界: 固壁采用无滑移条件. 由于针对FD-20的实验条件, 有效实验时间只有几十毫秒, 因此采用等温壁面条件Tw=295 K.

其中，

为主次应变速率之比的反正切值。

1.1.2 单向拉伸预变形

如图4所示，单向拉伸预变形在液压机上完成，为了在预变形后的二次加载中实现不同轧制方向的拉伸，单向拉伸预变形试样通常为非标准大尺寸试样（见图4（a））。使用万能试验机的标准夹具无法获得均匀应变场，为此基于大试样的几何形状和尺寸，设计了新型夹具（见图4（c））。为了获得尽可能大的均匀应变区，以便二次变形可以在不同方向上取样，先通过有限元建模仿真，确定“狗骨形”大试样的尺寸和夹持位置，仿真结果如图5所示，此夹持位置能满足应变均匀性要求。为了考虑轧制板料各向异性，“狗骨形”单向拉伸试样分别沿平行轧制方向（RD）和垂直轧制方向（TD）进行取样。

1.1.3 应变结果测定

以拉伸变形主导的预加载方式主要有3种，单向拉伸预变形、等双向拉伸预变形和平面应变预变形。等双向拉伸和平面应变预变形采用圆柱形平底凸模试验法（in-plane stretch forming test）完成，即Marciniak试验

。试验装置包括凸模、凹模和如图2所示的直径为

125 mm的平底圆柱凸模

，选用覆盖件常用材料AA5182铝合金。

试验结果与仿真结果产生误差的原因主要有：①凹模处润滑油的流动性差导致底部金属流动不均匀；②压力机精度产生的误差；③试样表面坐标网格不清晰产生的Argus测量误差。

被告:Yes.Send the phone number to…and track it down…(是的，把电话号码送去…追踪…)

在均匀预应变区，切割成形极限Nakazima试验样品如图9所示，完成成形极限曲线的测定。

1.2 二次加载下的成形极限图

考虑预变形加载条件的双线性应变路径是非线性加载中最基础的情形，能较好地代表薄板在多道次成形过程中的变形特点。A GRAF等

最先采用预变形方法探究板料在预变形状态下的成形极限，分别对2008 T4铝合金在平行和垂直于轧制方向进行了单向、等双向和平面应变拉伸预变形以及多个应变量的预拉伸，并对预拉伸后的板料在半球形凸模MTS成形试验机上拉伸来获得FLD。图10所示为板料经不同预变形加载后的FLD，研究发现双向预拉伸通常会降低整个FLD的成形极限，而单向预拉伸会提高FLD右侧的极限，但对左侧没有太大的影响，而平面应变预变形则会提高整体的成形极限。

A GRAF等关于非线性加载方式对FLC影响的研究结论被此后的多位学者所证实

。但是由于预变形方式的多样性，车身板件成形过程中首道次应变加载形式也复杂，需要进一步研究基于上述规律的成形极限预测方法。

2 与应变路径无关的成形极限预测

对于给定的成形工艺，板料在发生拉裂失效之前可能会发生变形直至极限应变，至今许多板料成形界的工程师仍然以基于应变的成形极限图作为板料成形的失效判据。然而，这仅在变形沿线性应变路径发生时有效，基于应变的成形极限图表现的路径相关性成为板料在复杂加载下成形极限预测不准确的主要原因，需要研究与加载路径无关的成形极限预测模型。

2.1 PEPS模型

R ARRIEUX等

首次提出了成形极限应力图（FLSD）的概念，研究发现FLSD与应变路径无关

。因此，FLSD对解决多道次加载条件下金属板料的成形极限预测问题具有重要意义。T B STOUGHTON

提出了不依赖于应变路径的基于极坐标的等效塑性应变（polar effective plastic strain，PEPS）模型，该模型是一种基于等效塑性应变极坐标表示的新型成形极限图，即PEPS FLD，实现方法如下。

为进一步加强双创教育，学院在上述三个指导教师团队的基础上，还明确全体任课教师双创教育责任，聘请社会上已经创业成功的优秀校友及其他优秀企业家，担任专业实践课和双创课的兼职教师。在对新进教师进行岗前培训时，学校将提高新进教师双创教育的意识和能力作为一项重要培训内容，达到每位专业教师都具备双创意识，从而更好地指导学生双创。

（1）应力应变转换。首先基于任意一种屈服准则（以Hill 48屈服准则为例），将极限应变转化为极限应力

。例如在平面应力状态下，考虑板料的厚向异性，Hill48屈服准则下的等效应力方程可表示为式（1）和式（2）：

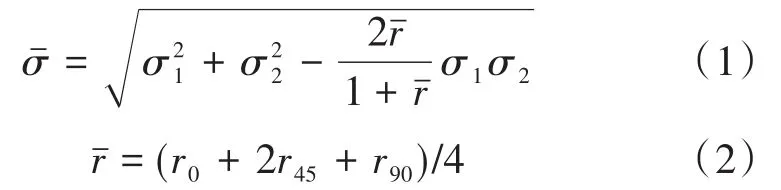
双线性路径的极坐标系等效塑性应变图实现原理

如图11（a）所示，Line1表示主应变方向成

角度的双向拉伸预变形，该预应变增量为（

e

,

e

），再以与主应变方向成

角度的单向拉伸变形直至断裂，由Line2表示。新的路径是根据等效塑性应变半径的大小和传统应变图中应变增量的方向确定，传统应变成形极限图用于定义新图中的方向，在新的等效塑性应变路径上的一条线投射回原点，如图11（b）所示。

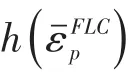
2.3 空白试验 对照实验是开展动物试验中的基本原则之一。按照国家相关规定，科学选用实验动物开展药效检验等实验，必须同时开展“空白试验”。中国药典进一步规范了动物试验的过程，明确了“空白试验”的做法，即在不加供试品或以等量溶剂替代供试液的情况下，按同法操作，对比两者所得的结果，由此探明实验结果和实验条件之间真实的因果对应关系。

由以上公式，在线性加载条件下，极限应变转变为极限应力，可用式（5）表示：

同时，等效塑性应变可用式（6）表示：

（2）极坐标系转换。通过式（7）可以将笛卡尔直角坐标系中的曲线转化至极坐标系。

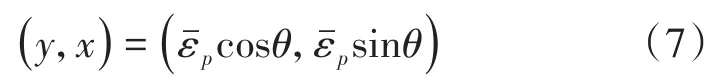
我国刑法第285条第一款非法侵入计算机信息系统罪规定：“违反国家规定，侵入国家事务、国防建设、尖端科技领域的计算机信息系统的，处三年以下有期徒刑或者拘役。”可以看出，我国刑法将该犯罪规定为行为犯，即只要违反国家规定，侵入了以上三个领域的计算机系统，就构成本罪。其中“违反国家规定”具体指违反《中华人民共和国计算机信息系统安全保护条例》第四条：“计算机信息系统的安全保护工作的重点在于维护国家事务、经济建设、国防建设、尖端科学技术等重要领域的计算机信息系统的安全。”或者《计算机信息网络国际联网安全保护管理办法》中第六条第一款：“未经允许，进入计算机信息网络或者使用计算机信息网络资源的行为。”

关于写话教学目标，《新课程标准》提出：1.对于写话有兴趣，留心周围事物，写自己想说的话，写想象中的事物。2.在写话中乐于运用阅读和生活学到的词语。3.根据表达的需要，学习使用逗号、句号、问号、感叹号。兴趣是最好的老师，对于刚开始规范运用汉字的低年级学生而言，从培养学生细心观察并善于表达的习惯，从而慢慢掌握运用字词句的规律。针对学生知识水平特点，充分利用表象思维引导学生写话，要引导学生根据阅读及生活中积累到的词语进行表达。

拉伸成形试验装置安装在双动液压机上或带有液压垫的单动液压机上。在变形坯料上方放置中间带有

30 mm圆孔的同形等厚的铜垫圈。凸模与垫圈之间采用固体润滑脂润滑，避免毛坯变形时出现边角破坏。通过面内拉伸成形试验，对试样进行等双轴拉伸的平面预变形。为了缩短试模时间提高试验效率，利用有限元模拟预判试验所需压边力、凸模下行高度、润滑要求等。图3所示为有限元模拟结果，中心平底区域主次应变均达到10%应变值，后续物理试验即参考有限元模拟所得的参数。

其中，

、

分别表示第一、第二主应力，

、

和

分别为与轧制方向成0、45°、90°时的各向异性系数，

ˉ为各向异性系数平均值。再定义最小主应力与最大主应力的比值为

。

任意路径下PEPS-FLD转换过程如图12所示。在主次应变坐标系中，多线段加载路径在该极坐标系中被转换成单一线性加载路径。极坐标系中曲线图与ε-FLD相比，优点在于两者形状相似。经不同的预变形加载条件获得的FLC曲线近似重合，如图13所示，表现出应变路径无关性，能有效解决非线性应变路径对成形极限图的影响。但是该模型是以平行于轧制方向的应变路径为前提提出，对于非轧制方向的加载路径是否适用还有待进一步研究。

对于一家企业而言，盈利是发展的基础，慕俄格酒店扎根方城，更在方城勇当酒店运营的标兵。今年8月，酒店积极联系毕节市、大方县婚庆公司，以合作的形式推出国庆黄金套餐，以市场为基准，不断优化酒店经营，为顾客提供优质的服务。不仅如此，酒店凭借优越的地理位置，积极拓展互联网渠道，与包括国内知名的旅游平台美团网、携程网、去哪儿网等达成酒店客房部业务合作，网上综合评分达到了4.8分，如今慕俄格酒店在整个毕节地区已家喻户晓，云南建投集团的影响力也随之节节攀升。

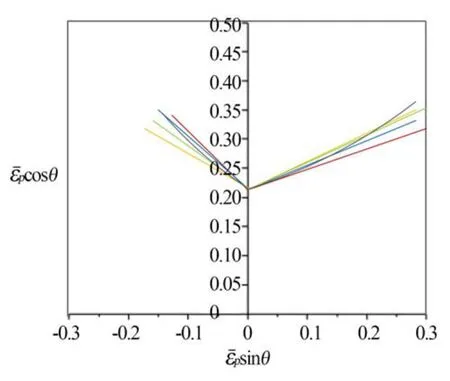
不同轧制方向获得的PEPS FLD是否存在差异，即PEPS模型是否考虑材料的各向异性，J ROJEK等

对单向拉伸（轧制方向上）13%预变形的DC04钢进行垂直和平行轧制方向的Nakazima试验

，并利用T B STOUGHTON等

提出的PEPS模型获取预变形板料的FLC，发现FLC在不同轧制方向上存在差异，如图14（a）所示。J ROJEK等

进而提出用厚度方向的应变|

|代替等效塑性应变，利用该方法得到的FLC具有较好的一致性，如图14（b）所示。

基于以上分析，PEPS模型的非路径依赖性较好地解决应变路径发生变化时传统FLD无法统一拟合的难题，可以为非线性加载下的板料成形极限的预测提供参考。S BASAK等

对AA5052铝合金分别进行了不同程度的单向拉伸预变形、等双向拉伸预变形和平面应变预变形，通过引入基于PEPS失稳模型发现其可以预测不同预变形板料的极限拉深比。

2.2 其他应变路径无关模型

除了PEPS模型，近年来学者也提出了多种应变路径无关的成形极限图方案

，如表3所示。

由于基于应力的成形极限曲线对应变加载路径依赖性较小，成形极限应力图（FLSD）可作为FLD的替代方案，从基于应变路径依赖的成形极限应变图转变到非路径依赖的成形极限应力图，来预测零件塑性成形结果。

其实我也早对市、区医院的专家们失去了信心，只不过我一直觉得为了一颗假牙抑或是北方较为寻常的支气管炎就去省城未免有点儿小题大做。兼或也有点儿和老婆置气的味道在里面。

3 结束语

综述了国内外关于成形极限预测的模型，并采用试验方法探讨了如何获得均匀预应变场，主要讨论了以下3点内容。

（1）能否使用统一的成形极限判定准则来消除各向异性带来的影响是亟待解决的问题。

（2）为使预应变具有可比性，应在预变形阶段设法获得均匀应变场，需在模具、夹具和应变量等方面进行合理设计，才可使二次成形极限具有可比性。

（3）为解决复杂加载条件下应变路径对成形极限预测的影响，需要引入路径无关的预测模型，工程师需改变使用传统FLD的习惯，转向FLSD，更多考虑多道次成形条件下非线性应变路径带来的预测误差。

[1]KEELER S P,BACKOFEN W A.Plastic instability and fracture in sheets stretched over rigid punches[J].ASM,1963,56(1):25-48.

[2]GOODWIN G.Application of strain analysis to sheet metal forming problems in the press shop[J].SAE Paper,1968,680093.

[3]GRAF A,HOSFORD W F.Effect of changing strain paths on forming limit diagrams of aluminum 2008-T4[J].Metallurgical Transactions A,1993,24(11):2503-2512.

[4]周蓉蓉,贺爱国,方华婵,等.预变形量对2219铝合金的力学性能及显微组织影响[J].材料热处理学报,2016,37(4):45-49.

[5]KOBAYASHI Y,TAKAHASHI J,KAWAKAMI K.Effects of dislocations on the early stage of TiC precipitation kinetics in ferritic steel:A comparative study with and without a pre-deformation[J].Acta Materialia,2019:176.

[6]MARCINIAK Z,KUCZYNSKI K.Limit strains in the processes of stretch-forming sheet metal[J].International Journal of Mechanical Sciences,1967,9(9):609-612.

[7]BIN,ZAMAN,SHAKIL,et al.Deformation-induced anisotropy of uniaxially pre-strained steel sheets[J].International Journal of Solids and Structures,2018,134:20-29.

[8]LAUKONIS J V,GHOSH A K.Effects of strain path changes on the formability of sheet metals[J].Metallurgical Transactions A,1978,9(12):1849-1856.

[9]韩 非,万 敏,吴向东,等.一种建立板料成形极限应力图的新方法[J].塑性工程学报,2007,14(4):1-5.

[10]朱险锋,王婷婷,庄新村,等.应变路径变化对材料韧性断裂的影响[J].锻压技术,2016,41(6):122-127.

[11]LAUKONIS J V.Anisotropic strain localization in tensile prestrained sheet steel[J].Metallurgical Transactions A,1981,12(3):467-472.

[12]HA J,FONES J,KINSEY B L,et al.Plasticity and formability of annealed,commercially-pure aluminum:experiments and modeling[J].Materials,2020,13(19):4285.

[13]何亚峰,干为民.基于LS-DYNA有限元平台火车车厢小弯梁板材成形研究[J].锻压技术,2013,38(1):40-44.

[14]ARRIEUX R.Determination and use of the forming limit stress surface of orthotropic sheets[J].Materials Processing Technology,1997,54:25-32.

[15]BASAK S,PANDA S K.Necking and fracture limit analyses of different pre-strained sheet materials in polar effective plastic strain locus using Yld2000-2d yield model[J].Journal of Materials Processing Technology,2019,267:289-307.

[16]夏 梦,顾苏楠,刘海亭.两种塑性失稳理论下的分散性颈缩极限预测[J].锻压技术,2015(9):128-133.

[17]YOSHIDA K,KUWABARA T,KURODA M.Path-dependence of the forming limit stresses in a sheet metal[J].International Journal of Plasticity,2007,23(3):361-384.

[18]STOUGHTON T B,ZHU X.Review of theoretical models of the strain-based FLD and their relevance to the stressbased FLD[J].International Journal of Plasticity,2004,20(8-9):1463-1486.

[19]STOUGHTON T B,YOON J W.Path independent forming limits in strain and stress spaces[J].International Journal of Solids and Structures,2012,49(25):3616-3625.

[20]STOUGHTON T B.A general forming limit criterion for sheet metal forming[J].International Journal of Mechanical Sciences,2000,42:1-27.

[21]STOUGHTON T B,YOON J W.Path independent forming limits in strain and stress spaces[J].International Journal of Solids and Structures,2012,49(25):3616-3625.

[22]ROJEK J,LUMELSKYY D,CHERSKI R P,et al.Forming limit curves for complex strain paths[J].Archives of Metallurgy&Materials,2013,58(2):587-593.

[23]ISO COPYRIGHT OFFICE.ISO 12004-2-2006 Metallic materials-sheet and strip-determination of forming limit curves-part 2:determination of forming limit curves in laboratory[S].

[24]YOSHIDA K,KUWABARA T,KURODA M.Path-dependence of the forming limit stresses in a sheet metal[J].International Journal of Plasticity,2007,23(3):361-384.

[25]PAUL S K.Path independent limiting criteria in sheet metal forming[J].Journal of Manufacturing Processes,2015,20(10):291-303.

[26]SIMHA C,GRANTAB R,WORSWICK M J.Computational analysis of stress-based forming limit curves[J].International Journal of Solids and Structures,2007,44(25):8663-8684.

[27]JOHNSON G R,COOK W H.Fracture characteristics of three metals subjected to various strains,strain rates,temperatures and pressures[J].Engineering Fracture Mechanics,1985,21(1):31-48.