压电陶瓷驱动高频喷射阀的结构设计

吕广雷， 马训鸣*， 李峙毅， 陈勇洁

(1.西安工程大学 机电工程学院， 陕西 西安 710600；2.西安工程大学 西安市现代智能纺织装备重点实验室， 陕西 西安 710600)

喷气织机具有运行车速快、生产效率高、物料消耗少、引纬方式合理，以及运转操作安全、简便[1]等优点，使喷气织机成为市场上应用较广、前景较好的无梭织机。喷气织机的气耗量占总能耗量的70%左右，辅助喷嘴占总气耗量的80%左右[2]。由此可见对辅助喷嘴起控制作用的喷射阀的性能直接影响织机的引纬质量和能耗。国内广泛应用的辅助喷嘴的控制阀是高频电磁阀，不但依赖进口，价格昂贵，而且受电磁铁本身的局限，响应频率低，造成能源浪费。

目前，由于压电陶瓷压电性能优越、响应速度快和耐久性好的特点，使其成为精准控制阀的首选材料。国内外学者对压电陶瓷驱动阀进行了深入的研究[3]。压电陶瓷驱动阀以不同的结构特征分为：先导型、直动型、喷嘴挡板型和开关型等4类。杨庆俊等[4]提出一种采用压电驱动器控制先导阀口开度的比例减压阀，通过Simulink软件分析了结构参数对阀的静态特性的影响。俞军涛等[5]提出了一种压电直接驱动伺服阀，设计了一种新型的液压微位移放大结构，对膜片结构进行了刚度和强度分析。彭畅等[6]提出了直动式喷嘴挡板式压电伺服阀，建立了数学模型，对阀的动态特性进行仿真。宋敏等[7]提出的压电高速开关阀，运用FLUENT对高速开关阀进行了动态流场分析。压电驱动器常用的结构类型分为：压电叠堆型，压电双晶片型等。解凯等[8]提出了一种叠堆式压电微喷阀，建立微喷阀的多场耦合模型，进行动态性能影响仿真分析。黄燕[9]提出压电先导型启动阀，采用悬臂式压电双晶片驱动结构，并对阀的驱动结构进行了仿真分析。

为了提高喷气织机的工作性能，减少能源消耗，课题组提出了一种基于压电驱动技术的新型压电喷射阀。通过ANSYS软件，对压电驱动器的静态特性、阀体的流场等进行综合分析,为压电喷射阀的优化设计提供了参考依据。

1 压电喷射阀的基本原理与系统建模

1.1 压电喷射阀的基本原理

在传统电磁阀的基础上，课题组将电磁阀的驱动装置改为压电驱动器，如图1所示。压电喷射阀由电源、进气口、出气口、压电弯曲片、凸台、阀体、密封垫和开关等组成。压电喷射阀采用喷嘴挡板式结构，挡板由压电弯曲片组成。当电源开关断开时，压电弯曲片靠开关阀预紧力关闭进气孔，停止工作。当电源开关闭合时，压电弯曲片通电，电场方向与极化相同的一侧产生位移收缩，另一侧则产生位移伸长，使压电弯曲片自由端产生位移，进气口打开，进气口与出气口形成通路，压电阀开始工作。

根据文献可知常用的压电驱动器有叠层式和双晶片式2种结构。压电叠层式驱动器的优点是对负载的输出位移和输出力大，响应时间短；缺点是驱动电压高，位移小，需要位移放大机构配合使用。而压电双晶片式具有结构紧凑、驱动位移大和驱动电压小等优点，但存在驱动力小的缺点。为了满足压电驱动器对力和位移的要求，选用pzt-5型号压电弯曲片，其由10层厚度为0.1 mm的弯曲片烧结而成，结构示意图如图2所示。

图2 压电驱动器示意图Figure 2 Piezo electric driver schematic

压电驱动器工作原理为：压电弯曲片通电，电场方向与极化相同的一侧产生位移收缩，另一侧则产生位移伸长，使压电弯曲片的自由端产生位移。位移S公式为[10]：

(1)

式中：L为压电弯曲片长度，mm；d31为压电常数，C/N；V为驱动电压，V；δ为压电弯曲片厚度，mm。

1.2 压电驱动系统建模分析

如图3(a)所示，压电陶瓷的电路模型可以等效简化为电阻R与电容C串联的模型，将其视为惯性环节[11-12]；如图3(b)所示，将压电驱动系统简化为质量、弹簧和阻尼系统[13]。根据电路平衡和力学平衡得：

图3 压电驱动器的等效模型Figure 3 Equivalent model of piezoelectric driver

(2)

(3)

对式(2)和(3)进行拉普拉斯变换并整理得：

(4)

(5)

联立式(4)和(5)得到输入电压、输出位移的传递函数为：

(6)

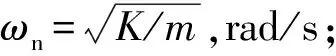
2 压电喷射阀的主要结构参数设计计算

2.1 压电驱动器的受力分析

作为压电喷射阀的核心驱动部件，压电弯曲片的参数和性能至关重要，由图1(b)可知当压电喷射阀停止工作时，进气口关闭。为了防止压电喷射阀气体泄漏并使其工作稳定，对压电弯曲片进行受力分析。

由图1分析得到压电喷射阀的受力模型为：

F1=F2+F3。

(7)

由胡克定律公式可得：

(8)

压电弯曲片的刚度公式[14]为：

(9)

课题组选择O型橡胶密封圈，密封圈预紧力[15]公式为：

(10)

挡板所受的气流冲击力主要由2部分组成：一部分为射流作用在挡板上的力；另一部分是控制腔的静压力作用在挡板上的液压力[14]。由公式得：

(11)

式中：F1为压电片的预紧力，N；F2为橡胶垫片对压电弯曲片的支撑力，N；F3为进气口的压力，N；x为压电弯曲片到凸台平面的距离，mm。EP为压电陶瓷弹性模量，GPa；δ为压电弯曲片厚度，mm；p1为工作压力，GPa；r1为进气孔的直径，mm；r2为凸台直径，mm；Cd为流量系数；h为工作间隙，mm。

2.2 压电喷射阀进气口的设计

压电喷射阀在进口处的压力p1为0.5 MPa，额定流量Q=20 L/min。压电驱动器为挡板式结构，则根据流量公式[16]与r1有如下关系：

(12)

根据受力分析可知h工作间隙由2部分组成：一部分为压电弯曲片驱动位移，另一部分为压电弯曲片受到气流力冲击变形产生的位移。由公式得：

(13)

将式(11)和(13)联立得工作间隙与进气口直径关系：

(14)

式中：Δp为压差，GPa；ρ为空气密度，kg/m3。

联立式(7)～(11)可以得到刚度K与r1成正比，刚度K与压电弯曲片的长度L成反比，L过长则压电弯曲片的刚度减小，导致压电喷射阀漏气；L过短则导致压电驱动位移短，无法满足工艺要求。由式(11)和(12)可知压电喷射阀额定流量Q与r1成正比，F3与r1成正比。r1过大时，F3将增大致压电喷射阀漏气，r1过小则无法满足压电喷射阀对流量的要求。为了保证压电喷射阀的驱动位移，首先确定压电弯曲片几何尺寸，然后再确定进气口r1的直径。综合考虑，设计压电弯曲片的几何尺寸为68 mm×20 mm×1 mm，单向驱动位移为1.5 mm，最大驱动力为24 N；r1为4 mm。满足压电喷射阀进口处的压力P1为0.5 MPa和额定流量Q为20 L/min的工艺要求。

3 压电喷射阀仿真

3.1 压电弯曲片刚度性能仿真

3.1.1 压电弯曲片刚度理论计算

将长度L为68 mm，宽度b为20 mm，厚度δ为1 mm，压电陶瓷弹性模量EP为56 GPa代入式(9)，可以得到刚度K=7 123.9 N·m-1。

3.1.2 压电弯曲片的刚度模拟仿真

建立压电弯曲片的几何模型，将几何模型导入ANSYS的static structural模块。导入的参数：L为68 mm，b为20 mm，EP为56 GPa，δ为1 mm，ρ为7 600 kg/m3，泊松比μm为0.36。在压电弯曲片的一端进行固定约束，使之成为悬臂梁状态，在自由端施加垂直方向负载F5=10 N，分析自由端的形变结果，得到形变结果X如图4所示。

图4 压电弯曲片形变XFigure 4 Piezoelectric bending sheet strain X

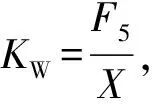
3.1.3 压电弯曲片的液动力刚度计算

为了保证压电弯曲片作为驱动器的高频阀的稳定性，就必须保证压电弯曲片的机械弹性刚度大于液动力刚度。

通过对式(7)求导可以求得液动力刚度[17]为：

(15)

根据工艺要求工作间隙h=1.5 mm，此时Ky取得最大值，Ky，max=6 785.8 N·m-1。

可得出结论：压电弯曲片的机械弹性刚度KW=7 123.9 N·m-1大于压电弯曲片的液压弹性刚度Ky，max=6 785.8 N·m-1，保证了压电弯曲片作为驱动器时的稳定性。

3.2 压电高频喷射阀流体仿真

由式(7)和(11)可得当r1与h增大时F3将增大，当F3大于F1时阀关闭状态下会出现漏气现象。而当r1过小时则无法满足压电喷射阀额定流量的要求；当间隙h较小时，出口的流速过小无法满足供气要求；当工作间隙h过大时，不但会降低阀的响应频率，同时也会造成大量的压缩气体浪费。所以选择合理的r1和h对压电喷射阀的设计至关重要。

3.2.1 网格划分

在FLUENT仿真中，网格划分质量会直接影响计算的收敛和计算的准确性，为了流场的精确计算，对模型进行了合理简化。在工作间隙等流场复杂区域进行局部加密，流场网格如图5所示。

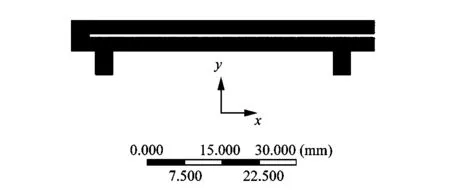
图5 网格划分Figure 5 Meshing

3.2.2 算法设置

根据计算，流场的雷诺系数Re>2 000，湍流模型选择RNG的k-ε，速度与压力耦合采用SIMPLE算法。保持计算精度，离散格式选择二阶迎风差分格式。

3.2.3 边界条件设置

入口边界设置为压力进口，工作压力设为0.5 GPa。面板设置包括进口压力、湍流能和湍流离散率等；出口边界设置为压力出口，操作压力设置为0 MPa；其余设置为壁面。

3.2.4 压电喷射阀的流量分析

改变进气口的工作间隙h的大小，工作间隙从0.3 mm依次增加到1.8 mm。进气孔r1分别选择3 mm，4 mm和5 mm。依据不同工作间隙和进气口对流量的影响进行仿真计算，仿真结果如图6所示。

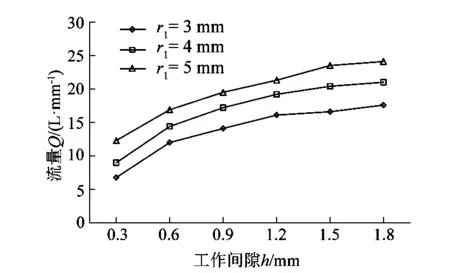
图6 流量分析Figure 6 Flow analysis

从图6中可以看出，在进气口直径r1一定的情况下，随着工作间隙h的增加，压电喷射阀的流量随之增加，当h增大到一定值后，压电喷射阀的流量增长趋势减缓；在工作间隙h一定的情况下，压电喷射阀流量随着进气口r1的增大而增大。由图可知当r1=4 mm，h=1.5 mm时，流量达到20.4 L/min，与式(12)描述情况和结果基本一致，满足工艺要求。

3.3 压电驱动系统的时域仿真

阻尼比是反映系统时间响应和稳定性的重要指标，表现在压电喷射阀的响应频率和控制精度上。利用MATLAB软件对压电驱动器的系统模型进行变量为阻尼比B的阶跃响应仿真 。

将阻尼比设为0.1到0.9进行仿真，图7为阻尼比对系统稳定影响的阶跃响应图。从图中可知，系统的调整时间和超调量随着阻尼比B的改变而变化，当B增大时系统的超调量随着B的增大而减小，当B=0.7时系统的超调量消失，压电驱动系统稳定。压电驱动器的阶跃响应时间为2 ms，压电驱动器的稳态输出位移为1.45 mm。

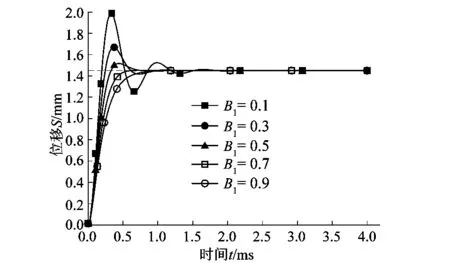
图7 阻尼比对系统的影响Figure 7 Effect of damping ratio on system

通过以上仿真得出结论：当等效质量m为0.002 4 kg，刚度取7 N/mm，系统模型的阻尼比B取0.7时，系统保持稳定，且响应时间稳定于2 ms。一般国产喷气织机引纬电磁阀的响应时间在5～8 ms内，设计的喷射阀响应速度相比高60%左右。

4 结论

课题组提出了一种应用于喷气织机引纬的压电喷射阀，对压电喷射阀的结构参数进行设计，建立模型，并对其进行仿真研究。通过对压电弯曲片刚度进行静力学仿真与计算，得出了合理的喷射阀流体动力刚度。通过ANSYS的FLUENT流体分析模块对压电喷射阀的内流场进行分析，确定了压电喷射阀的工作间隙，最后对压电驱动系统的时域进行分析，确认压电喷射阀具有良好的动态特性。结果表明：对比传统电磁阀，响应速度提高60%左右，无用气体消耗可减少约50%，达到节能的同时也为压电喷射阀后续机构优化提供了良好的基础和参考。