传感器弹性元件本构模型参数拟合研究

范海伦， 祖洪飞， 向 忠， 彭来湖

(浙江理工大学 机械与自动控制学院， 浙江 杭州 310018)

多维位姿测量[1]系统是保证机械手定位及轨迹精度的关键装置，传统的多维位姿测量多是通过多个单自由度位移传感器或编码器[2-3]来实现的，测量系统结构复杂，成本高，且容易产生多轴累积误差，难以满足精密位移测量的需求。因此，迫切需要一种精度高、结构简单的单体集成多维位姿传感器。通过测试对比，最终选取聚氨酯作为弹性体软轴的材料，在进一步研究该传感器传感特性的过程中，要对弹性体的运动及形变情况进行分析。由于聚氨酯为非线性材料，很难通过直接计算得到精确的解析解，因此通常需要借助仿真工具进行分析，而进行仿真分析的前提是要得到该材料的超弹性本构模型。本构模型描述了弹性体应力-应变关系，而其应力-应变关系是最终得到该传感器应变-位移关系的基础及核心，因此获得合适的超弹性本构模型就成为研究该传感器的关键所在。

对于弹性体材料的本构模型，国内外学者进行了大量的研究，并提出了多个模型：魏志刚等[4]基于弹性体的第1、第3主伸长率提出了一种新的本构模型，该模型对初始参数依赖小，只需通过试验就能获得较为可靠的模型参数，但该试验需构建特定的主坐标系，具有一定的局限性；冯希金等[5]针对未硫化橡胶，结合单轴拉压与剪切试验，使用Yeoh 应变能函数的广义Maxwell黏超弹性模型对未硫化橡胶进行拟合，发现该模型可以较好地描述未硫化橡胶的参数特征，为以后研究未硫化橡胶提供了一种新的思路；刘高冲等[6]对聚氨酯弹性体进行了静态与动态的单轴压缩试验，最终得到了聚氨酯弹性体与应变率相关本构模型，从而可以较好地描述应变率对聚氨酯弹性体的影响。上述文献对各种橡胶材料在不同的温度及不同的应变幅值下的本构模型进行了研究分析，但都是对弹性体应力-伸长比之间的关系进行研究，没有深入探讨应力-应变关系。

课题组以聚氨酯弹性体作为传感器弹性元件进行研究，研究了聚氨酯弹性体压缩状态下的本构模型，由于篇幅有限对于弯曲以及拉伸暂时不做研究。以圆柱状聚氨酯弹性体压缩试样为研究对象，在不同的应变率下对试样进行循环加载；然后，采用多种超弹性本构模型对其加载曲线的应力-应变关系进行拟合，对比分析各本构模型的拟合精度，选取最合适的本构模型。

1 弹性体材料本构模型

与金属材料的线弹性不同，聚氨酯等弹性体橡胶材料的应力-应变关系呈非线性变化，该类材料发生大变形后可以恢复原始状态，即变形可逆，因此可以看作超弹性材料，并且可以认为它们各向同性，对于此类材料，它们的应变能函数可表示为：

W=W(I1,I2,I3)。

(1)

式中：I1,I2,I3分别为Cauchy-Green变形张量的第1，第2，第3基本不变量。

超弹性材料的柯西应力张量可以表示为：

(2)

式中：p为静水压力，I为单位张量，B为变形张量。

对于单轴压缩、拉伸，设伸长率为λ，3个主伸长率关系为λ1=λ，λ2=λ3=λ-1/2，又由于超弹性材料可以看作各向同性不可压缩，所以I3=1。则：

(3)

将式(3)代入式(2)可推导出真实应力

(4)

又因真实应力σT与工程应力σ满足σT=λσ，则工程应力

(5)

1.1 Mooney-Rivilin本构模型

Rivilin在研究应变能函数一般形式时，推导出了各向同性不可压缩材料的应变能函数

(6)

式中Cmn为常数，且满足C00=0。

Mooney[7]在式(1)的基础上，取其前2项，其他各项的Cmn=0,有：

W=C10(I1-3)+C01(I2-3)。

(7)

式(7)被称为Mooney-Rivilin公式。将式(7)代入式(5)可求得Mooney-Rivilin模型应力-伸长率关系式：

(8)

伸长率λ与应变ε满足：λ=1+ε。式(8)整理后可写为:

(9)

将式(9)进行泰勒展开，因为ε最大为0.2，ε≫ε4，因此酌情保留到展开式的三次项或者四次项。

(10)

则Mooney-Rivilin模型应力-应变关系式为:

σ=2C10(4ε3-3ε2+3ε)+2C01(10ε3-6ε2+3ε)。

(11)

Mooney-Rivilin模型广泛应用于现代工程中，对拉伸不超过200%的橡胶材料试验数据具有较好的拟合，但是研究发现其对压缩试验数据拟合效果较差。

1.2 Yeoh本构模型

在Mooney-Rivilin本构方程的基础上，Yeoh[8]提出了3项应变能函数，该应变能函数只含有1个应变张量不变量I1，而不含有第2应变张量不变量I2，因此Yeoh本构方程也被称为减缩多项式方程。其应变能函数

W=C10(I1-3)+C20(I1-3)2+C30(I1-3)3。

(12)

将式(12)代入式(5)可求得Yeoh模型应力-伸长率关系式,整理后得到应力-应变关系式：

σ=2C10(4ε3-3ε2+3ε)+36C20ε3+54C30(-ε-1)。

(13)

因Yeoh模型不含有I2项,但是含有I1的更高次项，所以其对中等及以上应变具有较好的拟合效果，但是不能很好地描述等双轴拉伸状态。

1.3 Biderman本构模型

Biderman[9]在Yeoh模型的基础上增添了应变张量不变量I2，试验结果表明：单轴拉压状态下，相对于Yeoh模型，Biderman模型具有更好的拟合效果。其应变能函数

W=C10(I1-3)+C20(I1-3)2+C30(I1-3)3+C01(I2-3)。

(14)

整理得到应力-应变关系式：

σ=2C10(6ε5-5ε4+4ε3-3ε2+3ε)+2C01(21ε5-15ε4+10ε3-6ε2+3ε)+4C20(24ε5-15ε4+9ε3)+162C30ε5。

(15)

需要说明的是，由于最后一项C30系数展开式只有ε5，因此其他系数项皆保留到ε5。

1.4 Ogden本构模型

Ogden[10]并没有使用应变张量不变量表述橡胶本构的应变能函数，而是使用主伸长率来代替应变张量不变量，这样简化了描述应变能函数。其应变能函数

(16)

式中：i和n表示材料参数的项数；λi为主伸长率；μi，αi分别为试验确定的材料常数。

Ogden模型对材料的各种变形皆有较好的拟合效果，但是工程中一般使用不超过4项展开式，因为若超过4项，其拟合参数过多，迭代时间增加，误差增大，仿真困难。因此课题组选用Ogden模型3项展开式。工程应力

(17)

2 试验方法与试样

本试验所采用的聚氨酯压缩试样密度为1.2 g/cm3,邵氏硬度(90±2)A,直径为20 mm，高度10 mm的圆柱体，试验使用WDW-5电子万能试验机，并参照GB/T7757—2009进行。试验共制备5个压缩试样，分别对5个试样进行试验，取5次试验的平均值进行数据拟合。

试验仪器与试验材料如图1所示。课题组试验所用的工程应变为20%，分别进行0.010 0，0.001 0，0.000 3 s-1的3种应变率加载试验。试验先将测得的力-位移曲线转化为应力-应变曲线，再对转化后的应力-应变曲线进行本构方程拟合。最终得到不同工况下的最优循环加卸载本构模型。

图1 试验仪器与试验材料Figure 1 Test equipment and materials

弹性体材料在加载卸载时，其卸载应力要远低于加载应力，经过多次循环加载、卸载，其应力应变曲线才会几乎重合，这种现象就称为Mullins[11]效应。为消除Mullins效应，得到稳定加载曲线，需要在常温下对试样进行多次循环加载试验，此处采用的工程应变速率为0.001 0 s-1，最大工程应变为20%。

图2所示为聚氨酯压缩循环加载9次的力-位移曲线。加载过程中发现在第3次加载后力-位移曲线趋于稳定，在第5次加载后力-位移曲线基本稳定。获取稳定的加载力-位移曲线对于后续的弹性体受力分析和模型创建具有重要的意义，因为弹性体在循环加载、卸载的工况下工作，若使用未消除应力软化的数据进行分析会导致模型误差很大。因此，课题组在对试样循环加载、消除Mullins软化效应的基础上进行后续试验。

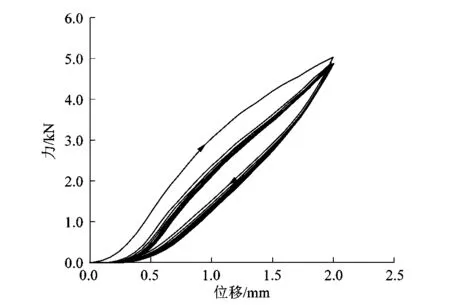
图2 循环加载力-位移曲线Figure 2 Cyclic loading force-displacement curve

3 本构模型的试验结果与分析

为获得合适的超弹性模型以准确地描述聚氨酯应力-应变关系，课题组分别对Mooney-Rivilin,Yeoh，Biderman以及Ogden这4种模型，在不同应变率下的数据进行了拟合分析。首先将试验所得数据进行处理，在试验机上直接测得力-位移关系数据，并将其转化为应力-应变关系，转换关系如下：

(18)

(19)

式中：F为加载力，d为试样直径，l0为初始厚度，l1为变形后的厚度，s为试验数据中的位移。

课题组没有使用传统的ABAQUS等仿真分析软件对其进行本构模型拟合，而是使用Origin专业绘图软件对其拟合。将试验数据整理后导入绘图软件中，使用非线性拟合将前文本构模型的应力-应变公式输入其中，实现对试验数据的拟合。试验得到应力-应变曲线如图3所示。

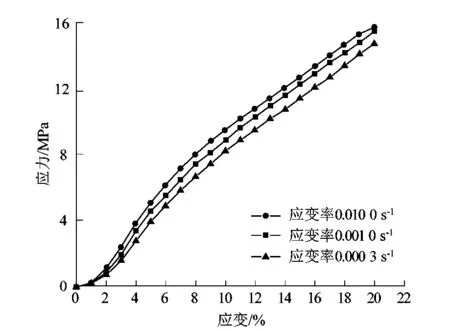
图3 压缩加载应力-应变曲线Figure 3 Compressive loading stress-strain curve

由图3可见，试验数据呈现“S”型，符合超弹性物质的性质。在3种加载应变率下，试验曲线形状几乎相同，在微小应变下曲线重合。在相同的应变下，随着应变率的增加聚氨酯弹性体受到的应力增大。

3.1 Mooney-Rivilin本构模型

如图4(a)所示，Mooney-Rivilin模型对3种应变率下的试验数据拟合偏离较远，尤其是在小应变情况下，这与其对压缩状态拟合较差的结论相符。在0%～3%应变范围内，拟合曲线呈现负值， 这与实际情况不符，且在应变达到17%左右时拟合曲线有应力减小的趋势，这与试验数据持续上升的趋势也相反。因此，我们认为Mooney-Rivilin模型不能对本试验所用的压缩状态下的聚氨酯弹性体应力-应变关系进行描述。

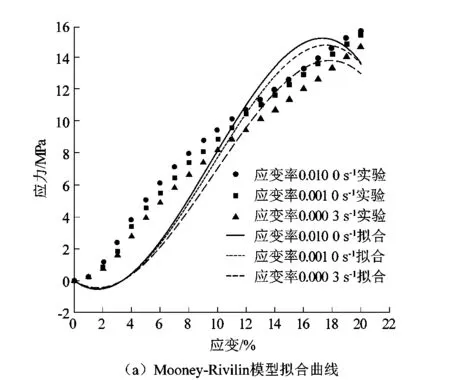
Mooney-Rivilin模型的拟合数据如表1所示。表1中C10为负值，而C01为正值，这与多数文献中对其他弹性体材料的拟合结果相反，一般情况下C10为正值，而C01为负值，这进一步说明了该模型不适合本试验中所使用的聚氨酯弹性体。

表1 Mooney-Rivilin模型拟合参数Table 1 Mooney-Rivilin model fitting parameters

3.2 Yeoh本构模型

图4(b)所示为Yeoh本构模型应力-应变拟合结果，可以看出Yeoh本构模型拟合效果明显优于Mooney- Rivilin本构模型。当应变为0%～4%时，Yeoh本构模型的应力高于试验数据较多；当应变为4%～12%时，Yeoh本构模型应力逐渐接近试验数据；当应变为12%～19%时，拟合效果最好。Yeoh本构模型拟合参数如表2所示。不同于硅胶等硬度较小的弹性体，课题组所采用的聚氨酯弹性体硬度较大，拟合参数第1、第3项为负值，第2项为正值，因此中等应变的拟合效果较好。

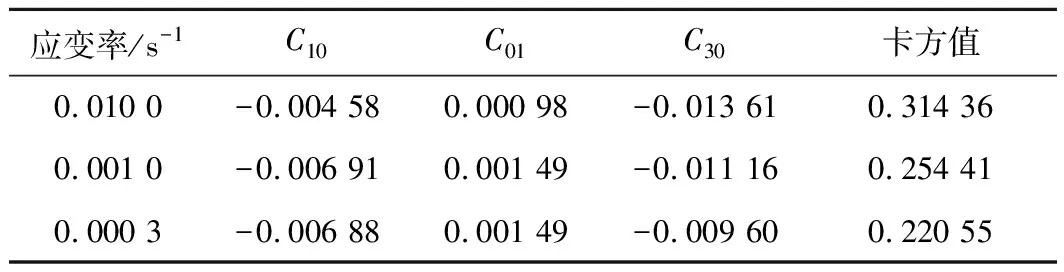
表2 Yeoh模型拟合参数Table 2 Yeoh model fitting parameters

3.3 Biderman本构模型

Biderman本构模型的拟合结果如图4(c)所示，拟合参数如表3所示。可以发现，Biderman本构模型在3种应变率下对试验数据的拟合效果均非常好，这表明Biderman本构模型能够很好地描述聚氨酯弹性体的受力情况。其原因是相对于Yeoh本构模型，Biderman本构模型增加了应变不变量I2项，参数也增加了C01项，因此不仅可以对小应变更好地进行描述，对中等应变以及大应变的契合程度也更高。

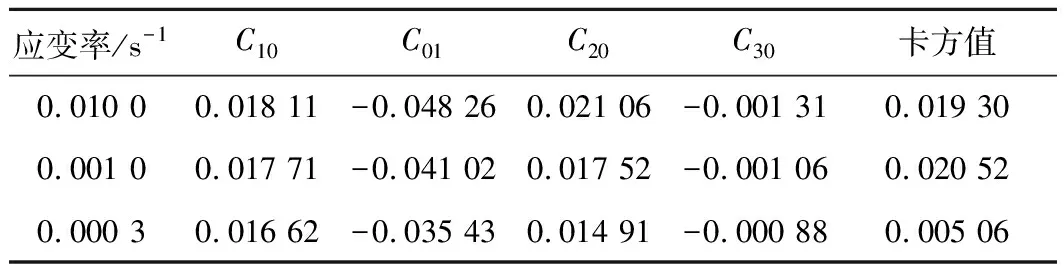
表3 Biderman模型拟合参数Table 3 Biderman model fitting parameters

3.4 Ogden本构模型

Ogden本构模型的拟合结果如图4(d)所示，拟合参数如表4所示。由拟合效果可知，Ogden本构模型对试验数据的拟合效果相对于Mooney-Rivilin、Yeoh这2种本构模型为佳，仅次于Biderman模型。在应变为0%～1%时，模型的应力为负值，这点与试验不符。Ogden本构模型对于试验试样大于2%的应变拟合效果较好。相对于前2种模型，Ogden本构模型具有更好的拟合效果，这与Ogden本构模型包含更多的参数有关，但因为Ogden本构模型参数较多，所以其拟合所需要的收敛时间更长，拟合参数的初始设定也更加繁琐。

表4 Ogden模型拟合参数Table 4 Ogden model fitting parameters

卡方值表示试验数据与拟合曲线的相关程度，如果卡方值小于0.05，则说明双方是显著相关的，也就是说拟合结果是符合的。卡方值大于0，数值越小表明相关性越显著，拟合效果越好。表5所示为4种模型拟合参数的卡方值对比，可以很明显地看出这4种模型在3种应变率下的拟合效果， Mooney-Rivilin和Yeoh 2种模型卡方值均大于0.05，不符合要求。Biderman模型与Ogden模型3种应变率下的卡方值均小于0.05，试验数据与拟合曲线显著相关，这2种模型卡方值对比可以看出相同应变率下Biderman模型卡方值更小，相关性更显著，拟合程度也就更好。

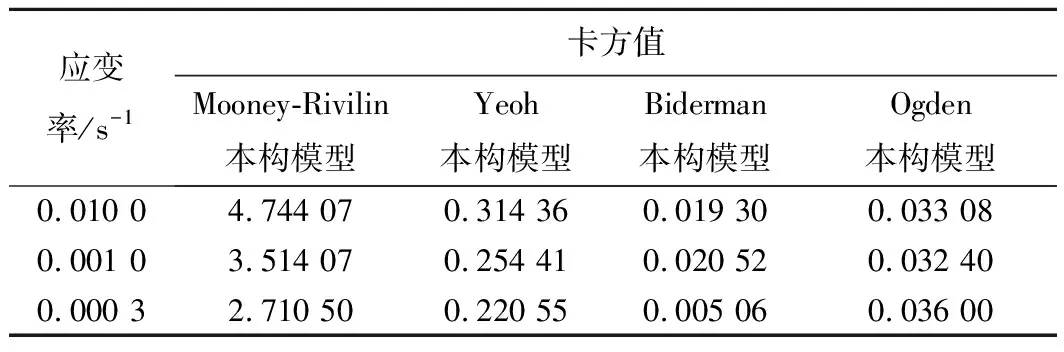
表5 4种模型拟合参数卡方值Table 5 Chi-square values of four-modelfitting parameters

4 结论

课题组使用电子万能试验机对聚氨酯弹性体进行准静态下压缩试验。对预处理试样进行不同应变率的压缩加载试验，将得到的数据处理之后导入专业绘图工具，最后利用4种本构模型对试验数据进行拟合。通过对实验数据拟合对比分析，可以得到如下结论：

1) 聚氨酯类弹性体具有应力软化效应，若要得到准确的实验数据，需要多次循环加载以消除Mullins效应。

2) Mooney-Rivilin本构模型对试验数据的拟合效果很差；Yeoh本构模型在小形变偏离较大而中等形变状态下拟合稍有偏离；拥有6个参数的Ogden本构模型对试验数据的拟合效果较好，但由于参数较多，收敛时间增大且初始值设定较为麻烦；对该试样拟合效果最好的是Biderman本构模型，不仅拟合程度最佳，并且参数数量适中，该模型能够很好地描述聚氨酯单轴压缩加载状态下的力学行为。

3) 本研究应力-应变曲线的拟合为后续材料的仿真建模提供了可靠的前提条件以及对进一步研究聚氨酯材料的热力学行为和黏弹性行为提供了一定的参照。