纱线卷绕成型过程叠纱机理及防叠方法研究

张与超， 张 华

(1.浙江理工大学 机械与自动控制学院， 浙江 杭州 310018；2.浙江理工大学 浙江省现代纺织技术重点实验室， 浙江 杭州 310018)

纱线在卷绕过程中具有较强的周期性规律，在卷绕到某些直径时会出现参数耦合，从而出现严重的叠纱现象。叠纱现象的出现会导致容纱量少、染色困难和机器震动等诸多不利影响[1]。针对叠纱问题，谢卫东等[2]提出了防止纱线重叠卷绕比确定方法，能有效解决叠纱问题；但是在实际应用中，纱筒的直径实时变化，难以测量，因此在生产中这种方法不适用。Wei等[3]介绍了一种最优分散绕线的方法，即绕线过程按照纱筒的直径使用分散的卷绕参数进行卷绕成型，卷绕过程中控制比较复杂，而且也需要实时测量绕线直径，在生产中并不适用。Zhou等[4]提出了基于双闭环PI调节器防叠方法，需要根据负载驱动器的电流反馈，调整输出转矩；此方法是基于槽筒导纱的方案，实现对槽筒转速的摆频控制达到防叠目的。实际应用中槽筒的摆频防叠效果一般，并且槽筒导纱方案对槽筒要求较高，使得生产成本较高。防止叠纱问题也有纯机械的方案[5-9]，对机构设计的要求比较高，后期的维护也比较麻烦，适用于传统的齿轮箱导纱方案。笔者着重研究纱线出现重叠现象的机理及如何避免该现象的方法，提出一种开环周期动态卷绕比防叠算法。该算法在横动导纱头移动的过程中，周期性改变纱线卷绕比，即卷绕速度与横动速度之间的比例，可减小叠纱概率。此方案只需要在伺服速度控制中控制单位时间内脉冲数量的偏差即可实现，不需要测量纱线实时直径等参数；以较低的成本，方便有效的方式解决纱线的叠纱问题。

1 纱线运动模型及叠纱机理分析

1.1 纱线卷绕成型运动模型

线筒被卷绕摩擦辊带着转动，纱线卷绕过程可以视为2个运动的合成：纱线在线筒上沿着切线方向卷绕和沿着轴向方向往复运动。线筒每卷绕一圈纱线将在线筒上形成一个螺旋线，当导纱头到达成型行程的边缘时，导纱头换向运动；此时将会在线筒上形成一个折返点，这个过程一直往复循环就会在线筒上形成2个反向的面纱，线筒的半径随着循环的进行逐渐变大。此过程周期性比较强，当多次往返点在线筒边缘的同一个位置时，将会看到多股纱线在线筒上同一个位置绕出同样的螺旋线，而横向导纱与卷绕的速度将影响螺旋线的螺距，当螺距明显而且多股纱线螺旋线叠加时就会形成明显的叠纱现象。纱线卷绕成型主要由卷绕电机提供纱线在纱筒上的切向运动，横动伺服电机提供纱线在纱筒上沿着轴向的周期往复运动，如图1所示。在此过程中对纱锭形状在不同的后续工艺中有着不同的要求。通常比较重要的要求是纱线在成型过程中2端面的纱线不能落纱，即在2端面不能形成蜘蛛网；其次叠纱问题也比较重要，叠纱现象会导致纱筒的震动，染色过程染料不易浸透导致染色出现不良品等问题[10]。

图1 纱线卷绕成型示意Figure 1 Schematic of yarn winding forming

1.2 叠纱现象及理论分析

纱线在线筒上的运动轨迹可以看成横动导纱的速度与线筒切向运动纺线的合成。切向线速度为：

vj=n*π*d。

(1)

式中：vj为卷绕速度，n为纱筒转速，d为纱筒直径。

导纱头的横动运动速度为vL,则2个速度的合成速度:

v=vL+vj。

(2)

卷绕角度：

(3)

导纱头在筒子宽w的行程内做往复运动，则纱线会在筒子上形成方向相反的螺旋线。将线筒沿着径向展开，则可以得到一个长方形形状,图2为纱筒沿着径向展开图。

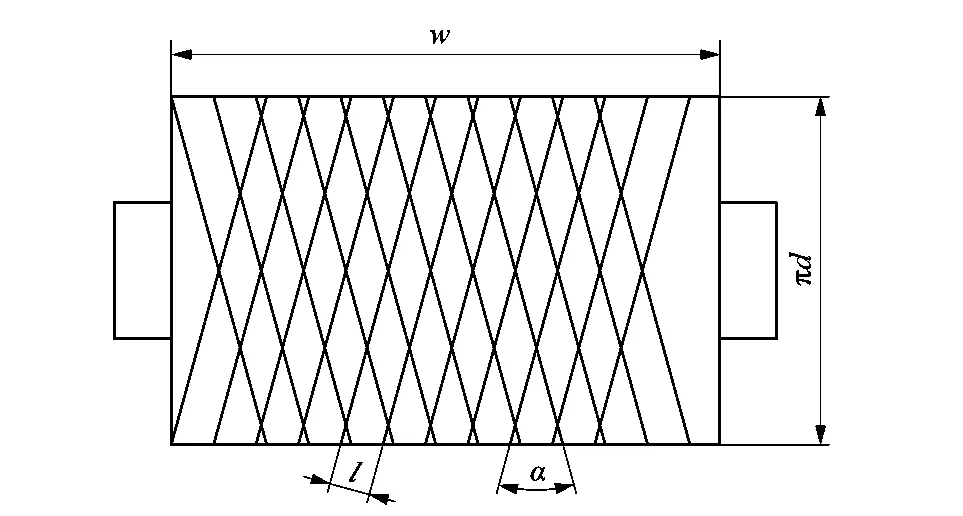
图2 纱筒径向展开Figure 2 Bobbin radially expansion

根据展开图建立数学模型，如图3所示。假设纱线是一个刚体A,从原点O(0,0)以具有x轴方向的横动速度vL和沿着y轴方向的卷绕速度vj在坐标系内运动，刚体在坐标系内沿着合成速度方向轨迹1运动，当运动到矩形上边时，此时刚好卷绕一整圈。由于矩形是纱筒的展开图，则令A的y坐标等于0，x坐标不变，沿着轨迹2运动，依次沿着轨迹3，4运动。当运动到矩形右边时，此时到达最大行程w，横动的导纱头换向。根据展开图，会等角度沿着轨迹5运动，并且以此沿着6，7和8运动。纱线便是如此往复循环运动，在线筒上形成一层又一层面纱，这就是纱线卷绕成型的过程。

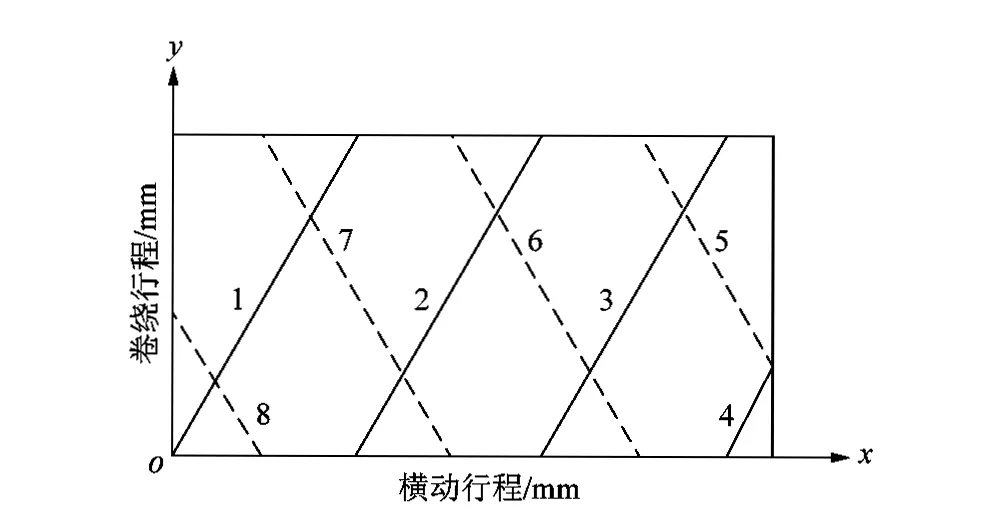
图3 卷绕过程数学模型Figure 3 Mathematical model of winding process

通常以端面折回点的分布情况来判断纱线的重叠情况，端面重合点分布均匀，且折回点较多，则认为纱线重叠现象较轻，如图4所示。

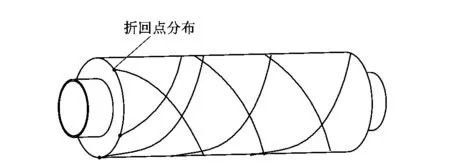
图4 端面折回点分布Figure 4 Distribution of return points

当导纱头往复1次时，时间为:

t=2w/vL。

(4)

式中t为导纱头往复1次的时间。

此时筒子卷绕圈数:

(5)

式中m为纱线在纱筒上卷绕的圈数。

当m为正整数时，则折回点刚好重合，就会产生叠纱现象。

在实际应用中，导纱头的横动速度vL和卷绕速度vj为固定值。按照大卷装倍捻机的工艺参数，卷绕角度α=24°，vj=100 m/min,则计算得：

(6)

将参数输入到MATLAB模型模拟纱线卷绕过程，可以直观地看到绕线过程的叠纱现象，如图5所示。

图5 数学模型仿真Figure 5 Mathematical model simulation

假设筒子直径d=80 mm，筒子宽度w=200 mm，卷绕角度α=24°，重叠周期为T(表示导纱头往复多少次会叠纱),则纱线重叠条件为:

(7)

式中k为任意正整数。可以得出：

(8)

假设以文中所提供参数计算，可得d=299.2*(T/k)。当重叠周期为T=1，此时重叠直径d有：299.2，149.6和99.7 mm。根据实际生产要求，d的取值范围通常为80～500 mm。表1为计算出来的重叠周期1～4的叠纱半径。

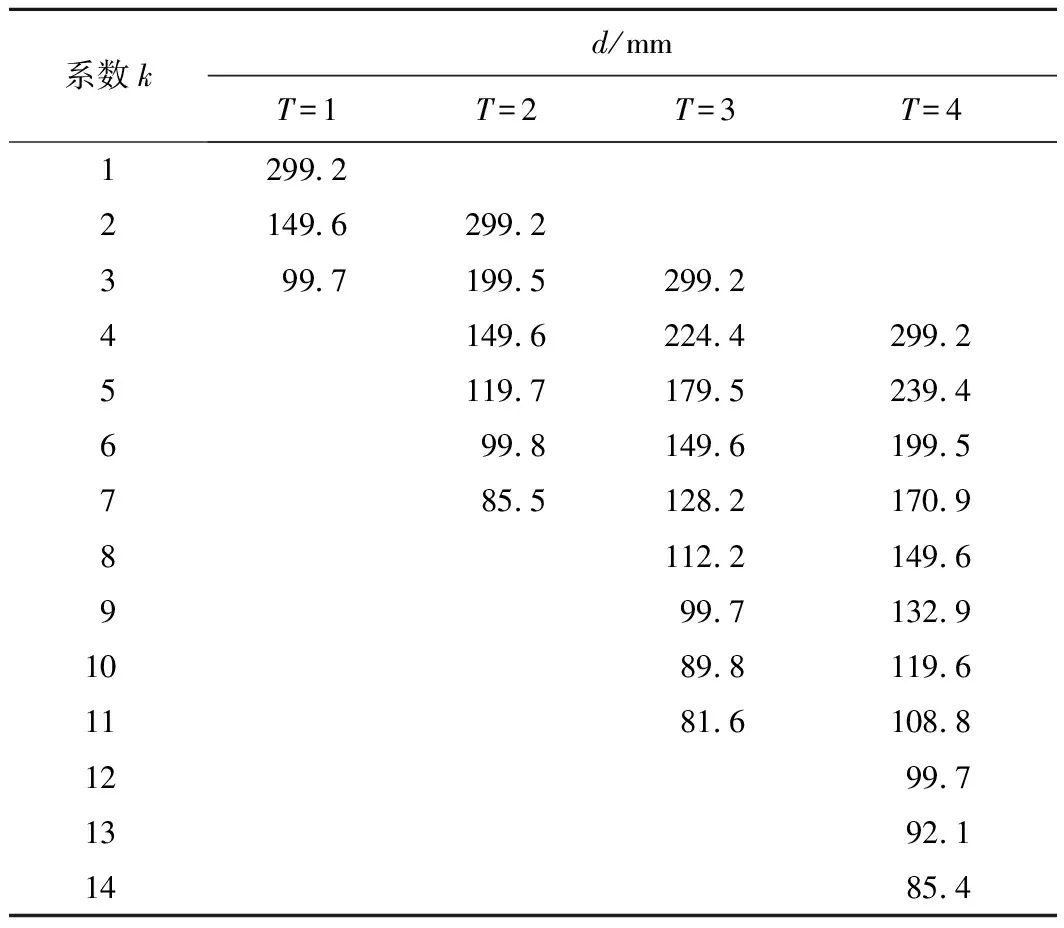
表1 叠纱直径计算结果Table 1 Calculation results of stack diameter

表1中的数据为折回点完全重合的情况。若考虑折回点偏移量很小时，叠纱直径会更多。在这种周期性强且时间长的情况下，叠纱现象明显。

1.3 周期动态卷绕比防叠算法

根据1.2节中将纱面展开得到的长方形纱线运动模型，可以知道纱线的重叠程度和导纱行程、纱筒直径及卷绕速度与横动速度之比有关。而这些因素当中，纱线的行程由工艺决定；筒子直径通常是个常数，不能随意更改；纱线的卷绕速度又会影响纱线的捻度，因此不能变动；所以要解决纱线成型过程中的叠纱问题只能从横动电机上想办法。横动电机通常采用伺服电机，便于实时控制其速度与位置。横动电机的速度会影响导纱过程中纱线的螺距和卷绕角等参数，从而影响纱筒的外观。由于伺服电机在换向过程中会有加速减速的情况，在长时间的累积下，纱线的2端会产生硬边，或者行程弧形边缘，影响纱锭质量。而解决办法是对横动伺服电机加减速过程中累积的纱线做出补偿，即让横动速度周期性地产生一个微小偏差来解决叠纱问题。基于此笔者提出了一种周期动态卷绕比防叠算法。

2 算法的设计及仿真

2.1 周期动态卷绕比防叠算法的设计

将导纱头的一个往复运动作为纱线成型过程中的最小运动周期。卷绕比是指导纱头往复运动1个周期，纱线在线筒上卷绕的圈数，通常计为J。根据定义得：

(9)

根据式(7)和(9)得:

J*T=k。

(10)

因此卷绕比的变化必然导致叠纱的变化。通常纱线的直径非常小，一般化纤小于0.007 8 g/m(70 D)，因此纱筒直径的增长非常慢，此时周期T和k都是常数，固定的卷绕比必然引起明显的叠纱现象。周期动态卷绕比防叠算法是在纱线的卷绕过程中将卷绕比按照一个动态的规律去变化，从而降低折回点周期重叠的概率和次数，达到减少叠纱的情况。卷绕比的变化过大将会影响纱线夹角的变化，根据式(10)，只需卷绕比轻微地变化即可改变k值，使之不等于正整数。因切向速度会对捻度产生重要影响，通常由工艺确定，而不能轻易改动。因此只有改动横动速度才能使动态卷绕比的数值满足设计要求。周期动态卷绕比的变化规律对防叠的效果也会产生影响。根据横动速度波动规律设计2种不同控制曲线。

1) 横动速度使用三角波的变化方式进行周期变化，如图6所示。横动基础速度vL可根据式(6)计算；波动中的最小速度v2=0.95vL,最大速度v1=1.05*vL。

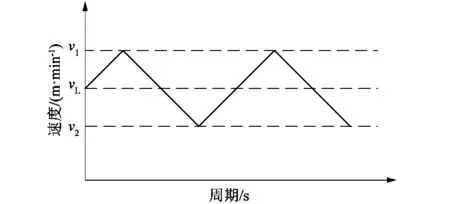
图6 伺服电机速度变化规律1Figure 6 Speed variation law of servo motor 1

2) 横动速度根据周期使用锯齿波的变化方式进行周期变化，如图7所示。

图7 伺服电机速度变化规律2Figure 7 Speed variation law of servo motor 2

2.2 周期动态卷绕比防叠算法的仿真

将以上2种速度波动规律曲线的周期动态卷绕比防叠算法在MATLAB上进行仿真。仿真模型参数如下：空筒直径为85 mm,满筒直径为260 mm,横动行程为160 mm,卷绕角度为30°,运行时间为400 min,防叠周期为20,速度波动为5%。在不进行防叠算法设计时，很明显在某些直径的时候，换向发生严重的重合现象，如图8所示。

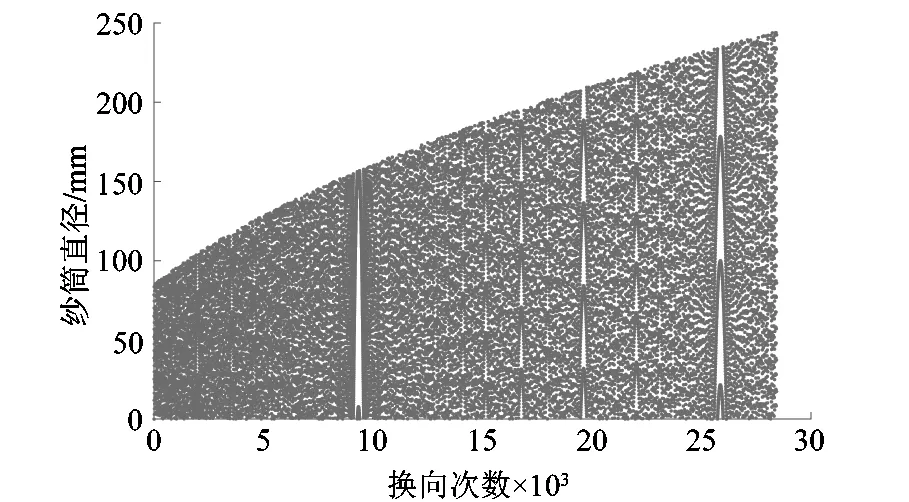
图8 折回点分布规律1Figure 8 Distribution law of return points 1

在使用2.1节中三角波的速度变化规律时，可以看出换向点分布比较均匀，仅在少数直径时，有轻微的重合现象，如图9所示。

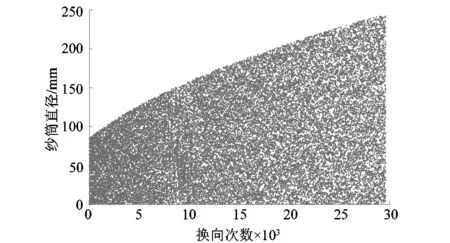
图9 折回点分布规律2Figure 9 Distribution law of return points 2

在使用2.1节中锯齿波角波的速度变化规律时，可以看出换向点分布比三角波效果更好，几乎没有重合现象，如图10所示。

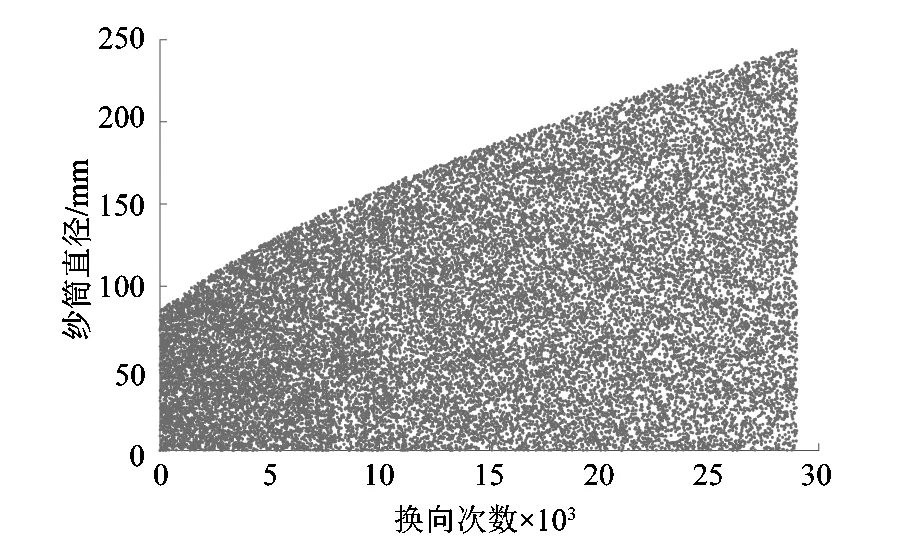
图10 折回点分布规律3Figure 10 Distribution law of return points 3

从仿真效果来说，2种速度波动规律都有良好的防叠效果，因此周期动态卷绕比防叠算法可以满足生产需求。

3 算法在倍捻机系统的实验

未经过防叠算法处理的纱筒如图11所示。

在倍捻机系统进行算法移植实验。该系统横动导纱电机采用的伺服系统有17位精度的编码器，具有较高的动态响应能力；卷绕速度与锭子速度均用霍尔传感器实时采样，速度控制精准。将算法移植到该平台，进行多次对比实验，得到的效果如图12所示。

图12 防叠算法效果Figure 12 Anti stacking algorithm effect

4 结论

基于仿真实验及实际测试，周期动态卷绕比防叠算法在纱线电子成型系统中有较好的防叠效果。在仿真试验中，由于锯齿波速度有突变，有利于防叠，因此仿真结果好于三角波。在实际试验中，横动速度按照三角波波动规律，纱线成型角度波动均匀，机器振动小。按照锯齿波波动规律，横动速度有突变，机器振动情况比三角波幅度大，而且纱线卷绕面没有三角波美观。对比需要实时采集纱线直径的防叠算法，笔者提出的算法成本较低，容易部署，并且稳定性更高。纱线防叠在纺织行业是一个难点，更好的防叠算法能够进一步提高纱锭的质量，从而提升后道工序乃至成品的质量，因此防叠算法的研究具有重要的意义。