两能级量子系统的固定时间控制及鲁棒性
柳 松,匡 森
(中国科学技术大学自动化系,安徽合肥 230027)
1 引言
量子控制作为多学科交叉研究领域,对量子科学与技术的发展有极大的推动作用[1-2].目前,最优控制[3]、Lyapunov控制[4-5]、神经网络控制[6]、容错控制[7]、学习控制[8]等方法已被广泛用于量子系统的控制中.实现量子系统的固定时间控制(即在外部控制场的作用下,在某个与初始态无关的固定时间内实现量子系统状态的准确控制)对实用化量子信息技术具有重要意义.例如,在核磁共振(nuclear magnetic resonance,NMR)量子计算机中,人们有必要在独立于量子态的固定时间内实现系统的完全收敛,以更高效地通过一系列射频脉冲来生成表征量子逻辑门的期望幺正变换,减小对邻近量子位的影响[3].
量子系统的有限时间控制问题,是指在外部控制场作用下系统可以在有限时间内稳定到期望的目标态,但其收敛时间函数依赖于初始态.而固定时间控制总能在一个与初始态无关的常数时间内使系统稳定收敛.例如,连续非光滑控制[9-10]被用来实现系统关于目标本征态的有限时间稳定;滑模控制[11]、π脉冲法[12]、几何控制原理[13]、最优控制技术[14]都可以通过在一个预先给定的时间内设计合适的控制律来实现系统在固定时间内的完全布居数转移,但都要求满足一定的约束条件.
在量子系统的实际应用中,不可避免地存在噪声和不确定性.例如,对于固体核磁共振自旋系统,外部噪声磁场以及与其他自旋间的耦合有可能导致系统哈密顿量上的不确定性.Dong等人[11]结合Lyapunov控制和周期投影测量提出了一种滑模控制方法,以实现对系统哈密顿量上不确定性的鲁棒控制,该方法需要精确设计投影测量的周期.文献[15]提出了一种基于采样学习的数值方法,用于哈密顿量中包含不确定性的量子系统的鲁棒最优控制设计.文献[10]研究了控制哈密顿量上的不确定性对量子系统有限时间稳定性的影响.然而,实际量子系统的初始态有时并不容易精确获得,在实验操作中也可能出现控制场的波动[16],这些因素都会导致状态转移的偏差.
本文基于固定时间稳定性理论针对两能级量子系统设计含分数幂的连续非光滑控制律,以便实现系统对于目标平衡态(纯态和混合态)的固定时间收敛性;提出了两种非光滑切换控制方法以解决某些分数幂取值引起控制性能差的问题;论文也分析了实际应用中可能存在于系统哈密顿量、初始态和控制场上的不确定性对系统固定时间控制的影响.
2 问题描述
2.1 系统模型和控制目标
本节考虑在一个控制场作用下的两能级封闭量子系统,其状态演化过程可用刘维尔方程表示:

其中:密度算符ρ是描述量子态的半正定厄米算符,u1为标量实值外部控制场,H0和H1为系统的内部和控制哈密顿量,且

为简化分析,本文中将约化普朗克常数ħ设置为1.此外,将满足[H0,ρ]=0的状态称为系统(1)的平衡态.
在相干矢量[17]表示下,任何定义在希尔伯特空间的两能级量子系统的状态ρ均对应欧几里得空间R3中唯一的一个实矢量,即
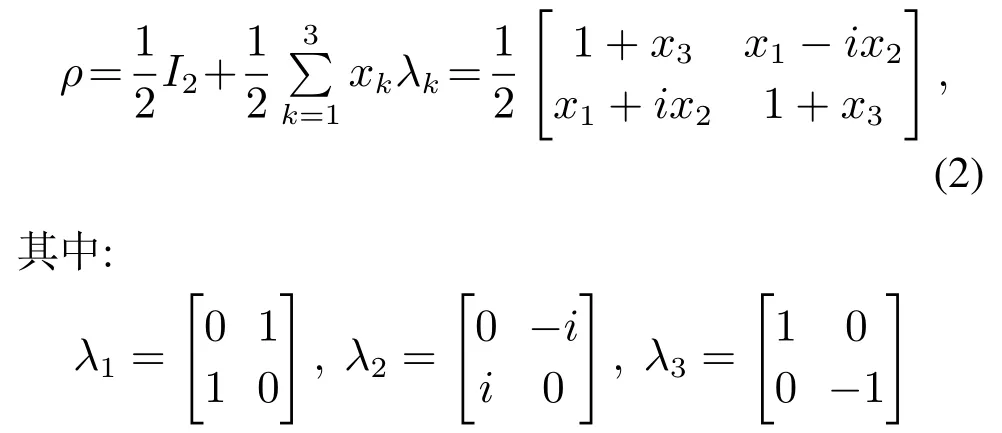
为泡利矩阵,xk=tr(ρλk)表示系统在λk上投影的期望值,x=[x1x2x3]T称为ρ的相干矢量或Bloch矢量.所有Bloch 矢量的集合构成了两能级系统(1)的Bloch 空间.定义矢量模长当a=1时,系统状态为纯态,对应三维欧式空间单位球面上的点;当a<1 时,量子态为混合态,对应R3单位球内的点;当a=0时,量子态位于R3单位球的球心,此时系统(1)处于完全混合状态.
为了便于分析系统对于目标平衡态的固定时间收敛性,本文基于式(2)的形式和复数的指数表示进一步将系统的密度矩阵写为

注1通过对系统状态采用式(3)的指数表示形式,可以采用类似于文献[9]的方法将系统方程(4)最终写为一个单变量微分方程的形式,从而便于讨论系统的固定时间收敛性.
2.2 相关定义和引理
对于仿射非线性动态系统:

引理1[18]考虑非线性系统(5),假设存在一个连续径向无界的函数V:Rn →R满足下列条件:
1)V(x)=0⇒x=0;
2)V(x)>0,x ∈Rn{0};
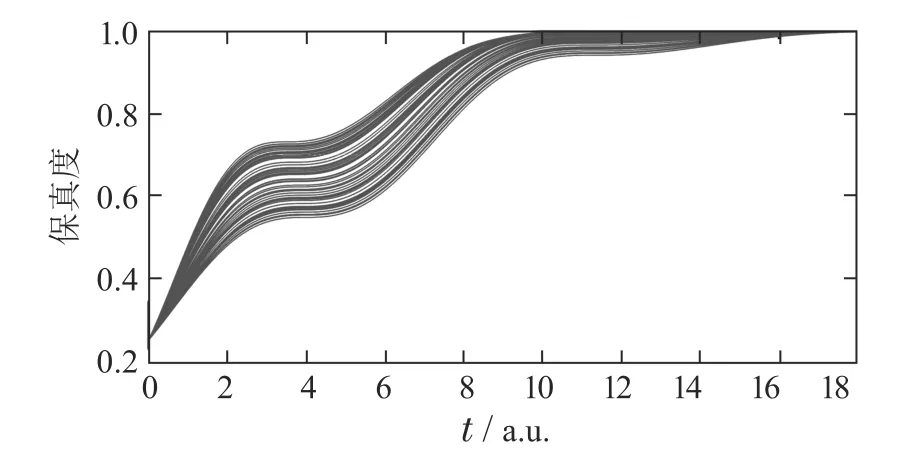
3) 存在正实数α>0和0 那么,系统(5)的原点是有限时间稳定的,且有限收敛时间函数满足 定义1[19]如果非线性系统(5)的原点是全局有限时间稳定的,且有限收敛时间函数是全局有界的,那么称系统(5)的原点是全局固定时间稳定的,即存在Tmax∈R+使得T(x(0))≤Tmax,∀x(0)∈Rn. 引理2[18]假定原点是非线性系统(5)的一个有限时间稳定平衡点,且存在一个包含原点的开邻域U ⊆Rn使得对于任意x(0)∈U收敛时间函数都是连续的,那么存在正实数p ∈(0,1)和连续正定函数V:U →R使得对于任意x(0)∈U,˙V在U上都是实值连续的,且存在正实数α>0使下列不等式成立: 引理3[18]考虑非线性系统(5),假定存在一个包含原点的开邻域U ⊆Rn和一个连续函数V:U →R.令Ωκ={x ∈U:V(x)<κ,κ>0},且存在一个连续函数P:R→R满足P(κ)>0.如果x:[t1,t2)→U是一个满足x ∈的连续函数,且对于任意x(t)∈U有下列不等式成立: 那么对于所有的t ∈(t1,t2),都有x(t)∈Ωκ. 为使系统在控制作用下稳定收敛到目标态ρf,选取如下的Lyapunov函数[5]: 经典非线性系统固定时间控制的研究表明[20],类似于式(12)的控制律可以用来实现被控系统的固定时间收敛性.然而,由于式(12)含有两个分数幂,分析和论证相对复杂.为了简化分析,本文中仅考虑一个分数幂的特殊情况,即分析两能级量子系统(1)在如下控制律作用下的固定时间稳定性: 其中:K >0,0<γ <1. 由式(3)可得 根据式(11)(13)-(14)可知,量子系统在向目标态ρf转移的过程中,(ρ)=0出现的条件和控制哈密顿量的选取有关.考虑以下情况: 当r2=0时,由于r1和r2满足,此时系统处于给定的目标平衡态ρf.由式(10)-(11)(13)可得V=0,=0,u1=0,这说明系统状态不再发生变化. 假定系统的控制哈密顿量满足hI=0,那么当系统(4)的状态在集合M={ρ:r2/=0,sinφ2=0}中时,满足sinφ2=0的量子态构成了单位球面(纯态)或球内(混合态)上φ2为π或2π的一个圆. 将系统(4)演化过程中满足r2/=0,sinφ2=0的非目标态记为ρτ,相应的时刻记为tτ.根据系统(4)的第4个方程可得 式(15)说明存在时刻t1>tτ,使得量子态的相位角φ2在非光滑控制律(13)的作用下从φ2(tτ)=µπ,µ=1,2,演化到φ2(t)/=µπ.由式(13)-(14)可知u1(t)/=0,t ∈(tτ,t1],这意味着集合M中的量子态一定会在区间(tτ,t1]内的某个时刻离开集合M,继续向目标态ρf演化. 同理,可分析出当hR=0或当hR/=0,hI/=0时系统(4)在非光滑控制律u1作用下的演化情况. 由于控制律u1作用下的系统(4)是非Lipschitz连续的,因此无法直接利用Lipschitz连续性条件来判断系统解的存在唯一性.由式(15)可知,对于给定的目标态,满足=0的、非目标态的所有量子态构成了一个过渡态集合.根据文献[9]的定理5易知:对于任意初始态,两能级量子系统(4)在控制律u1作用下存在唯一的连续可微解. 考虑到式(3)表示的量子态始终满足sinφ1=0,且当目标态满足ρf1>ρf2时,有cosφ1=1;当目标态满足ρf1<ρf2时,有cosφ1=-1.因此,在控制律(13)作用下的系统(4)可写为 这样,分析系统(17)从初始状态[r1(0)r2(0)]T到平衡点[a0]T的固定时间控制问题就相当于分析系统(19)的变量r2在固定时间内从初始状态r2(0)收敛到原点所满足的条件. 对于系统(19),可给出如下固定时间稳定性定理: 观察控制律(13)可知:当分数幂因子γ →0时,控制律(13)将逼近棒棒Lyapunov控制,因此控制后期的状态转移性能将变差[5];当γ →1时,控制律(13)具有明显的标准Lyapunov控制特性,导致量子系统的完全收敛时间较长.对此,可以提出两种非光滑切换控制策略,即基于不同分数幂和不同比例系数的切换控制策略,以保证两能级量子系统(19)具有更好的固定时间控制性能. 当分数幂γ较小时,大量的仿真实验表明:对于集合D中的任意量子态,若控制律(13)的比例系数K保持不变,则选择较大的分数幂可以使得系统在新的控制律作用下具有更好的控制性能;而若分数幂γ保持不变,则适当减小控制律的比例系数K,仍可使得系统更好地向目标态演化.其中,第j个控制律的固定时间作为分数幂为γ(j)(或比例系数为K(j))和分数幂为γ(j+1)(或比例系数为K(j+1))的控制律之间的切换条件,系统的总固定收敛时间为,j=1,2,···.需要注意,γ(j)和K(j)的个数及其具体值的选取不是唯一的. 注3本文设计的控制律(13)和这里提及的切换控制律都是解析形式的非光滑控制律,主要用来实现固定时间内系统对于目标态的准确收敛性.而传统的光滑控制则很难完成这样的控制任务.事实上,相对于光滑控制而言,非光滑控制通常能够完成更复杂的控制任务,目前已在量子系统控制中得到了广泛研究和应用[5,21-25]. 量子系统的不确定性可近似描述为系统哈密顿量的扰动ΔH0、初始态的偏差Δρ0和控制场的波动Δu1.本文中,将系统哈密顿量的不确定性记为 将控制场的波动记为|Δu1|≤σ,σ >0.此时的量子系统模型可表示成 图1 当初始态为ρ0时,量子态保真度和非光滑控制律的变化曲线Fig.1 The evolution curves of fidelity and the non-smooth control law for the initial state ρ0 图2 当初始态为ρ0时,量子态保真度和不同比例系数的切换控制律变化曲线Fig.2 The evolution curves of fidelity and the non-smooth switching control laws with different values of K for the initial state ρ0 接下来,采用不同分数幂的非光滑切换控制方法对目标混合态进行仿真.假定系统初始以0.95的概率处在本征态|1〉,同时又以0.05的概率处在叠加态,即初始态为 则其纯度为tr()=0.9525.通过数值计算可知ρ0的两个本征值可近似为0.0243和0.9757.进一步,假定系统的目标态为 设置控制律(13)中的比例系数为K=0.3,两次非光滑切换控制的分数幂分别为以 为切换条件.仿真结果如图3所示.根据图3和仿真数据,系统收敛于目标态的总时间满足 图3 当初始态为ρ0时,量子态保真度和不同分数幂的切换控制律变化曲线Fig.3 The evolution curves of fidelity and the non-smooth switching control laws with different values of γ for the initial state ρ0 这同样与理论结果一致. 在连续非光滑控制律u1和标准Lyapunov控制律=-Ktr(i[H1,ρ]ρf)的作用下,系统哈密顿量和初始态上的不确定性对量子态保真度的影响分别如图4-5所示.显然,对于这两类不确定性,非光滑控制比标准Lyapunov控制具有更强的鲁棒性.此外,根据理论分析和图4可知,自由哈密顿量的不确定性不影响系统状态的保真度. 图4 在非光滑控制和标准Lyapunov控制作用下,系统哈密顿量的不确定性对量子态保真度的影响Fig.4 Under non-smooth control and standard Lyapunov control,the influence of the uncertainty in the system Hamiltonian on the fidelity of quantum state 图5 在非光滑控制和标准Lyapunov控制作用下,初始态上的不确定性对量子态保真度的影响Fig.5 Under non-smooth control and standard Lyapunov control,the influence of the uncertainty in the initial state on the fidelity of quantum state 假定控制场的不确定性Δu1在区间[-0.5,0.5]上服从均匀分布,则图6显示了非光滑控制场(13)的波动Δu1对量子态保真度的影响(60次仿真).从图6可看出,受扰动量子系统最终进入了包含目标态的一个邻域内,这说明非光滑控制对控制场上的有界不确定性有较好的鲁棒性. 图6 当非光滑控制场u1的不确定性Δu1为区间[-0.5,0.5]上均匀分布的扰动时,量子态保真度的变化曲线Fig.6 The evolution curves of the fidelity of quantum state when the uncertainty Δu1 in the non-smooth control law u1 obeys a uniform distribution on the interval[-0.5,0.5] 针对两能级量子系统,本文借助Lyapunov方法设计了一个包含分数幂因子的连续非光滑控制律,基于固定时间稳定性定理给出了系统在一个与初始态无关的固定时间内关于目标平衡态(纯态和混合态)收敛的条件.针对分数幂的某些取值可能导致收敛性能差的问题,本文提出了两种非光滑切换控制策略,并通过仿真实验验证了该方法的确能够有效改善系统的控制性能.对于实际量子系统中可能存在的不确定性,本文也通过将其近似描述为系统自由哈密顿量、控制哈密顿量、初始态和控制场上的有界扰动分析了它们对系统固定时间稳定性的影响.应该说明,尽管本文仅考虑了一个控制场的情况,但相应的控制律设计方法和稳定性分析方法完全适用于多个控制场的情况.然而,对于多能级量子系统,由于很难将系统方程变换为单变量微分方程的形式,因此在固定时间稳定性的论证上需要引入更多的理论工具.此外,测量反馈影响下随机开放量子系统的固定时间控制以及自适应鲁棒固定时间控制问题也是值得研究的问题.
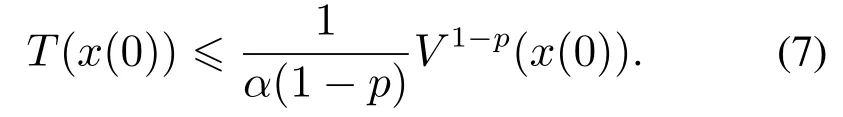
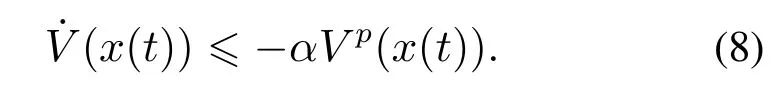

3 固定时间控制和稳定性
3.1 固定时间控制器设计


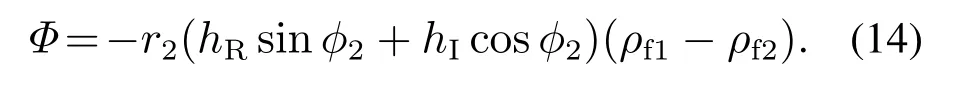


3.2 固定时间稳定性



3.3 性能改进
4 鲁棒性分析



5 数值仿真

5.1 固定时间控制验证



5.2 性能改进验证


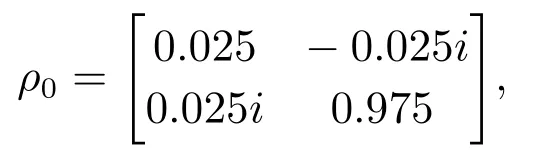




5.3 鲁棒性验证




6 结论

