簇中心初始选择策略与更新异权机制相耦合的MDBA算法
吴 涛,高雷阜,荣雪娇,高金鑫
(辽宁工程技术大学优化与决策研究所,辽宁阜新 123000;辽宁工程技术大学运筹与优化研究院,辽宁阜新 123000)
1 引言
在探索与挖掘分析大数据的背景下,基于时间序列的数值型数据在生物医学[1]、机械工程[2]、金融预测[3]等多领域普遍存在,其有效快速的识别与获取已成为数据研究领域中的热点问题.在时间序列的挖掘过程中,对时间序列的历史数据进行聚类、分类和回归等操作时,利用适当的度量方法计算两条时间序列间的相似性不但是时间序列分析的关键步骤,而且对数据挖掘的效率和精度有直接的影响.
时间序列相似性度量的经典方法主要分为“一对一”比较的锁步度量法和“一对多”相比的弹性度量法两种类型[4].欧氏距离[5]以计算简单且易于理解等优势成为锁步度量中最为普遍的相似性度量方法,但其度量前提要求两条时间序列长度相等,否则度量结果误差较大.相较于锁步度量法,弹性度量可对两条时间序列展开“一对多”或“一对0”的比较以克服两条变相时间序列的度量结果误差较大的难点.常见的弹性度量方法有编辑距离(edit distance,ED)[6]和动态时间弯曲(dynamic time warping,DTW)[7-8]两种度量.其中,由于动态时间弯曲是根据两个时间序列的拉伸或收缩匹配来计算序列间的相似性,克服了欧氏距离无法解决的扭曲或变形的时间序列的匹配问题而逐渐被应用.
动态时间弯曲质平均(DTW barycenter averaging,DBA)[9-10]算法通过DTW确定序列的对齐方式,由对齐方式确定匹配点,每次迭代时平均当前簇中心各位置的所有匹配点更新簇中心.但初始簇中心的选取具有随机性,可能导致每次迭代后簇中心长度不一.此外,平均数据集中所有序列和当前簇中心的所有匹配点来更新簇中心,忽略了数据集中每条序列的差异性,可能导致簇中心在迭代时惯性收敛速度缓慢.
鉴于此,为消除初始簇中心选取的随机性和解决簇中心迭代时收敛速度慢的问题,避免迭代次数和最终惯性增加,从而引起算法复杂度的增加和降低迭代效率,本文提出了一种耦合簇中心初始选择策略和更新异权机制的改进DBA算法(merge DTW barycenter averaging,MDBA).簇中心初始选择策略利用时间序列数据集中选择惯性最小时间序列作为初始簇中心,簇中心更新异权机制在更新时平均每个序列和簇中心对应的匹配点的平均值作为下次迭代时的簇中心.通过实验对比分析发现,DBA算法在加入簇中心初始选择策略时最终的簇中心惯性接近DBA算法中初始簇中心随机选取的惯性均值;加入更新异权机制后簇中心在迭代时惯性收敛性优于原算法,部分数据集最终的簇中心惯性优于原算法;MDBA算法的收敛性和最终簇中心质量显著优于原算法.
2 动态时间弯曲质平均(DBA)算法理论
2.1 动态时间弯曲(DTW)
任意给定两条时间序列,长度不等时若用欧氏距离计算距离,长度较长的时间序列可能存在无对应位置的点,基于此思想,长度较长的时间序列中必须有多个点对应长度较短的时间序列中的同一点,为了保持时间序列的有序性,当多个点对应一个点时,多个点必须是相邻点.较短的时间序列亦可多个点对应长度较长的时间序列中同一个点,如图1所示.

图1 两条不等长序列的一种对齐方式Fig.1 An alignment method of two unequal length sequences
对齐方式的多样性导致距离计算的结果存在多样性,其中距离最短的对齐方式即为关键路径.

DTW能够在序列之间找到全局最优的对齐方式,并且成为度量序列相似性的最常用的方式,也可以度量长度不等的序列相似性.
2.2 动态时间弯曲质平均(DBA)
设序列数据集Data={T1,T2,T3,···,Tn},为了描述时间序列数据集的总体形态特征,需要用一条时间序列来刻画整个数据集的特征,这条时间序列称为数据集的簇中心[16].簇中心到数据集中其它序列的距离和应当尽可能的小,为了衡量这一数值,将簇中心和数据集中所有序列的距离平方和称为惯性,最优簇中心应当是所有序列中惯性最小的序列,即最优的簇中心f应当满足:对任意时间序列X:
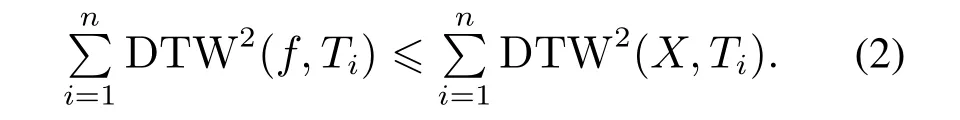
在时间序列聚类过程中,需要对数据集不同类别分别求得簇中心,而DBA算法通过平均对应位置的所有匹配点来求得簇中心.
设时间序列数据集Data={T1,T2,T3,···,Tn},则该算法具体执行步骤如下:
步骤1随机选取数据集Data中的一条序列Tg,其中g ∈{1,2,3,···,n},取初始簇中心f=Tg;
步骤2计算当前簇中心f与数据集中所有序列的动态时间弯曲关键路径P1,P2,P3,···,Pn;
步骤3将关键路径中所有与f1匹配的数据求平均作为新的f1,所有与f2匹配的数据求平均作为新的f2,所有与f3匹配的数据求平均作为新的f3···所有与fm匹配的数据求平均作为新的fm;
步骤4重复步骤2-步骤3直到满足终止条件.
步骤5输出f.
3 融合DBA算法
3.1 簇中心初始选择策略
DBA算法中的初始簇中心的选取方式是从数据集中随机选取一条序列,从簇中心迭代的最终结果来看,这样很可能导致多次实验的结果不稳定,其中包括簇中心的长度和每个点数值大小;从迭代次数来看,可能会出现迭代次数过多或者过少的情况,算法每次的运行时间相差较大;从算法的应用上来看,为了提高聚类的准确率,会多次使用DBA算法寻找更好的簇中心,但是多次使用DBA算法必然会导致聚类任务时间的增多,对于每次随机产生的聚类结果,最终求均值以克服算法的随机性,均值结果必定会差于多次随机产生的最优结果.
为了克服DBA算法的初始簇中心选取策略的随机性,提出了簇中心初始选择策略(initial slection strategy,ISS),在初始簇中心的选取上,选取数据集中惯性最小的时间序列作为初始簇中心.若对∀i ∈{1,2,3,···,n},均有
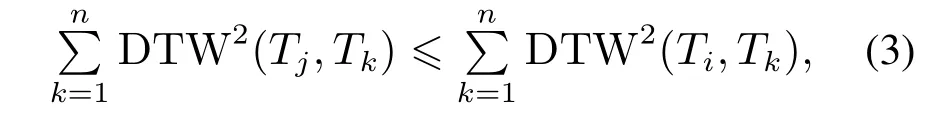
则Tj为初始簇中心.
3.2 簇中心更新异权机制
DBA算法中簇中心每次迭代时对簇中心的每个点的所有匹配点求平均,忽略了各个序列的差异性,将所有序列对簇中心的影响力视为一致.但通常情况下,每个序列对簇中心的影响可能是不同的.为了充分应用每个序列的差异性,提出了簇中心异权更新机制(updated weight mechanism,UWM).
若簇中心f中的点fj对数据集中任意序列Ti匹配点为,则簇中心异权更新后

DBA算法步骤2和步骤3是算法迭代的关键步骤,对簇中心的每个点的所有匹配点求平均更新簇中心,忽略了序列之间的差异性,为了保留每个序列的个体特征,先平均每个序列对应的匹配点,最后平均所有序列对应匹配点的平均值作为每次迭代的簇中心.
两种改进方法在理论上可行,考虑到两种改进策略可以进行融合,于是提出MDBA算法,即在初始簇中心的选择上选择序列中惯性最小的序列作为初始簇中心,在簇中心的更新中对每个序列进行加权更新簇中心.其它步骤和原算法保持一致.
3.3 算法复杂度
仅对序列簇中心进行加权更新,算法的复杂度并无显著变化,可以忽略不计,所以只考虑初始簇中心选择策略对算法整体复杂度的影响.
设数据集D={T1,T2,T3,···,Tn},假设每个序列等长,Tk=,设DBA算法的迭代次数为I1,MDBA算法的迭代次数为I2.算法中关键步骤复杂度如表1所示.

表1 算法复杂度Table 1 Algorithm complexity
从复杂度的表达式可以看出,忽略阶梯项时融合DBA算法与原算法的复杂度基本一致.
3.4 MDBA算法步骤及流程
MDBA算法具体步骤如下:
步骤1为数据集中所有序列的DTW创建距离矩阵.计算数据集中的每个时间序列与其它所有时间序列的DTW,并用矩阵R记录下,矩阵R中的元素则有:Rij=DTW(Ti,Tj).
步骤2对距离矩阵中所有的列求和.对R中的每一列元素求和,并用向量sum记录下,向量sum中的元素则有:sumi=
步骤3记录下列元素之和最小列的序号.记录sum中最小的元素的序号l,即序号l应满足:suml=min{sum1,sum2,sum3,···,sumn}.
步骤4将该序号下的序列作为初始簇中心.初始簇中心f=Tl.
步骤5计算当前初始簇中心与数据集中所有序列的关键路径.计算f与数据集中所有时间序列的动态时间弯曲关键路径P1,P2,P3,···,Pn.
步骤6对每个关键路径中所有对应匹配点求平均.创建n条列向量{Q1,Q2,Q3,···,Qn},每个向量的维度均和f相同,将关键路径P1中所有与f1匹配数据求平均记为,所有与f2匹配的数据求平均记为,所有与f3匹配的数据求平均记为所有与fm匹配的数据求平均作为记为.同理根据关键路径P2求出Q2···根据关键路径Pn求出Qn.
步骤7对每个序列对应的簇中心求平均更新簇中心.将所有的列向量{Q1,Q2,Q3,···,Qn}中每个维度求平均作为f,即f=
步骤8判断迭代次数是否满足终止条件(或者新的簇中心惯性与前一次簇中心惯性差满足终止条件).重复步骤5-7直到满足终止条件.
为便于直观的理解该算法的求解步骤,绘制算法流程图,见图2.

图2 MDBA算法流程图Fig.2 Flow chart of MDBA algorithm
4 数值实验
为验证MDBA算法的有效性与可行性,通过3种改进策略簇中心在迭代过程中惯性变化和惯性收敛性,分别对每种改进算法进行惯性对比实验和收敛性分析.共设计3组实验,每组实验包括全局惯性变化和不同类别惯性变化.全局惯性变化实验对比原算法和改进策略的惯性质量,不同类别惯性变化实验验证改进策略的不同类别的数据惯性收敛性.
实验机器配置均为Inter i7 CPU 2.20 GHz,RMA 8 GB,Windows 7操作系统,MATLAB R2016a.每组实验均使用UCR数据库中的8个数据集,具体数据集参数如表2所示.

表2 数据集参数Table 2 Data set parameters
为了消除量纲的影响,对数据集中的每条时间序列使用Z-score标准化进行预处理.
4.1 簇中心初始选择策略的对比实验
为了验证簇中心初始选择策略对原算法的影响,本次实验合并测试集和训练集数据,不考虑数据集中数据的标签,迭代次数设为30次,DBA算法实验10次,取10次实验平均值作为每次迭代的惯性,实验结果如表3所示.

表3 各数据集迭代次数为30时惯性对比Table 3 Inertia comparison when iteration times of each data set are 30
由表3分析可知,在迭代次数为30次时,DBA算法在加入簇中心初始选择策略后惯性在DBA算法的平均惯性上下浮动,不超过11%.DBA算法加入簇中心初始选择策略后,惯性值接近DBA算法的惯性平均值,此策略在迭代次数为30次时,能够搜寻到接近原算法惯性平均值的簇中心.在实际应用中簇中心初始选择策略可以降低DBA算法的使用次数,从而降低总体迭代次数,降低算法复杂度,提高DBA算法的惯性质量.但是迭代次数小于30次时的惯性无法通过表3对比分析.
为了对比两种算法在迭代次数小于30次时的惯性,需要对实验过程中的每次迭代的惯性进行对比.对每次迭代时的惯性进行绘图,迭代时惯性变化见图3.

图3 各数据集初始簇中心惯性变化对比Fig.3 Comparison of inertia change of initial cluster center of each data set
由图3分析可知,在不同数据集中,随着迭代次数的增加,两种算法的惯性的惯性变化曲线出现多个交点,两种算法的惯性受迭代次数的影响,在迭代次数为10次时,加入簇中心初始选择策略的DBA算法最优惯性始终优于DBA算法最优惯性,即在迭代次数较少的情况下,簇中心初始选择策略有利于寻找最优簇中心.对于部分数据集,如ArrowHead,DistalPhalanx-TW,惯性随迭代次数增加,波动幅度较大.需要对簇中心初始选择策略的惯性收敛性进行分析.
为了验证簇中心初始选择策略的惯性收敛性,对数据集各个类别的数据均进行收敛性分析,本次实验合并数据集测试集和训练集中相同类别,对不同类别的数据使用加入簇中心初始选择策略后的DBA算法进行迭代,迭代次数为100次,各数据集中各类别的簇中心惯性变化见图4.
由图4分析可知,DBA算法在加上簇中心初始选择策略后,算法收敛性较为一般,部分数据集的不同类别数据惯性变化在较大的范围波动.例如Arrow-head数据集在进行分类后,各类惯性值波动较为明显,收敛过程并不平稳.


图4 各数据集不同类别的簇中心惯性变化Fig.4 Inertia changes of cluster centers in different categories of data sets
综上所述,加入簇中心初始选择策略后的DBA算法最终惯性接近DBA算法的惯性平均值,但收敛性较差,因此可以引入更新异权机制进行对比.
4.2 簇中心更新异权机制的对比实验
为了验证簇中心更新异权机制对原算法迭代的影响,本次实验合并测试集和训练集数据,不考虑数据集中数据的标签,迭代次数设为30 次,两种算法均实验10次,初始簇中心相同,取10次实验平均值作为每次迭代的惯性,实验结果如表4所示.
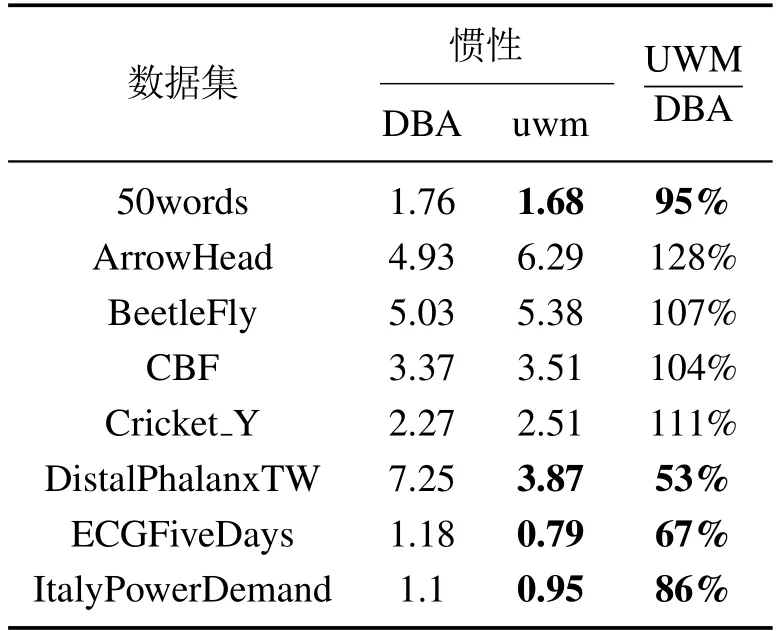
表4 各数据集迭代次数为30时惯性对比Table 4 Inertia comparison when iteration times of each data set are 30
由表4分析可知,引进簇中心更新异权机制后,各数据集惯性值变化效果比较明显,其中簇中心更新异权机制效果最好的为DistalPhalanxTW数据集,最终惯性值为DBA算法的53%,效果最差的为ArrowHead数据集,惯性值为DBA算法的128%.其中一半的数据集簇中心更新异权机制提高了惯性质量.为了更好的、更直观的对比簇中心异权机制对簇中心每次迭代的惯性影响,将迭代时的惯性变化绘制成图,结果见图5.
由图5分析可知,在引进簇中心更新异权机制后,部分数据集在迭代过程中惯性值始终优于DBA算法,如DistalPhalanxTW,ECGFiveDays,ItalyPowerDemand数据集.总体上,簇中心更新异权机制加强了原算法在迭代过程中的惯性收敛性.相比于簇中心初始选择策略,惯性值随迭代次数的增加,变化较为平稳.

图5 各数据集更新异权惯性变化对比Fig.5 Comparison of inertia changes of different weights updated by each data set
为了验证簇中心更新异权机制的惯性收敛性,对数据集各个类别的数据均进行收敛性分析,本次实验合并数据集测试集和训练集中相同类别,对不同类别的数据使用加入簇中心更新异权后的DBA算法进行迭代,迭代次数为100次,各数据集中各类别的簇中心惯性变化见图6.
如图6所示,DBA算法在引入更新异权机制后,对于数据集中不同类别的数据惯性变化较为平稳,个别数据集的个别类别的收敛过程呈水平直线,惯性收敛效果比加入簇中心初始选择策略的DBA算法好,原算法加入更新异权机制后有利于提高簇中心迭代效率,便于短时间内寻找最优簇中心.

图6 各数据集不同类别的簇中心惯性变化Fig.6 Inertia changes of cluster centers in different categories of data sets
引入簇中心更新异权机制后的DBA收敛性优于原算法,但惯性值一般,甚至出现高于原算法28%的数据.加入簇中心初始选择策略后的DBA算法,惯性值接近DBA算法的平均值,但收敛效果较差,收敛性较原算法并不突出.考虑簇中心确定性选择策略和更新异权机制两者各自特点,MDBA算法可能在提高迭代效率的同时提高簇中心惯性质量.
4.3 MDBA算法的对比实验
为了对比MDBA算法和DBA算法的惯性变化,设置迭代次数为30次,DBA算法实验10次,每次迭代的惯性取10次的惯性平均值.不考虑数据集中序列标签,合并数据集中测试集和训练集,当迭代次数为30次时,3种改进算法和原算法惯性值见表5.
由表5分析可知,融合初始选择策略和更新异权机制的DBA算法,惯性值最优的数据集为DBA算法的53%,相比于DBA算法,惯性值质量较差的数据集为Cricket-Y、DistalPhalanxTW,其中最差的仅比原算法的惯性值提高了10%.MDBA算法总体上提高了DBA算法的惯性质量.相比于初始选择策略和更新异权机制,MDBA算法对一半的数据集效果惯性值达到最优.
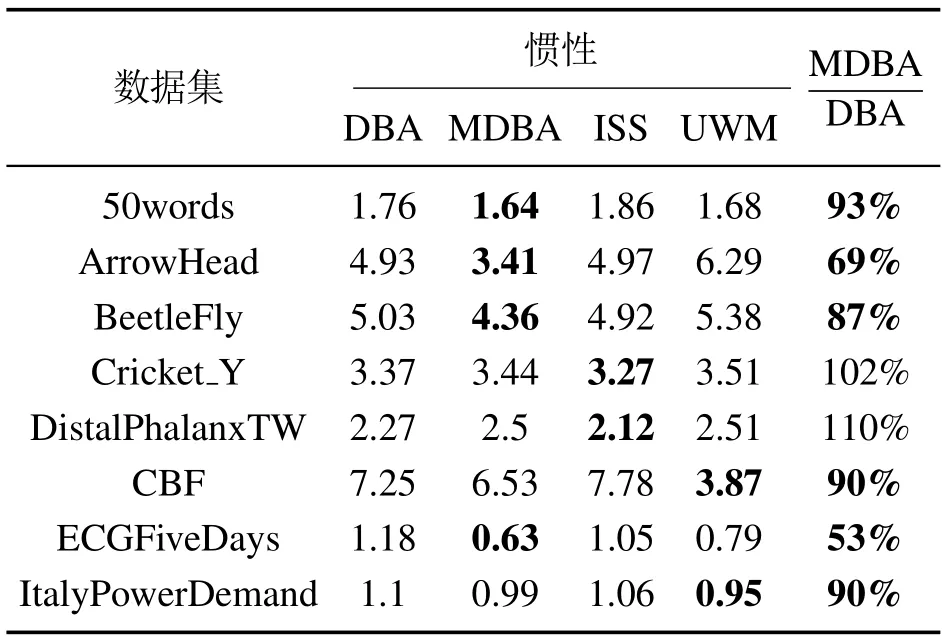
表5 各数据集迭代次数为30时惯性对比Table 5 Inertia comparison when iteration times of each data set are 30
为了更好的、更直观的对比MDBA算法和原算法每次迭代的簇中心惯性,将迭代时的惯性变化绘制成图,结果见图7.
由图7分析可知,在迭代过程中,MDBA算法总体上的惯性值小于DBA算法,在迭代次数小于5时能搜索到较优的簇中心,惯性值在迭代时变化较为平稳.

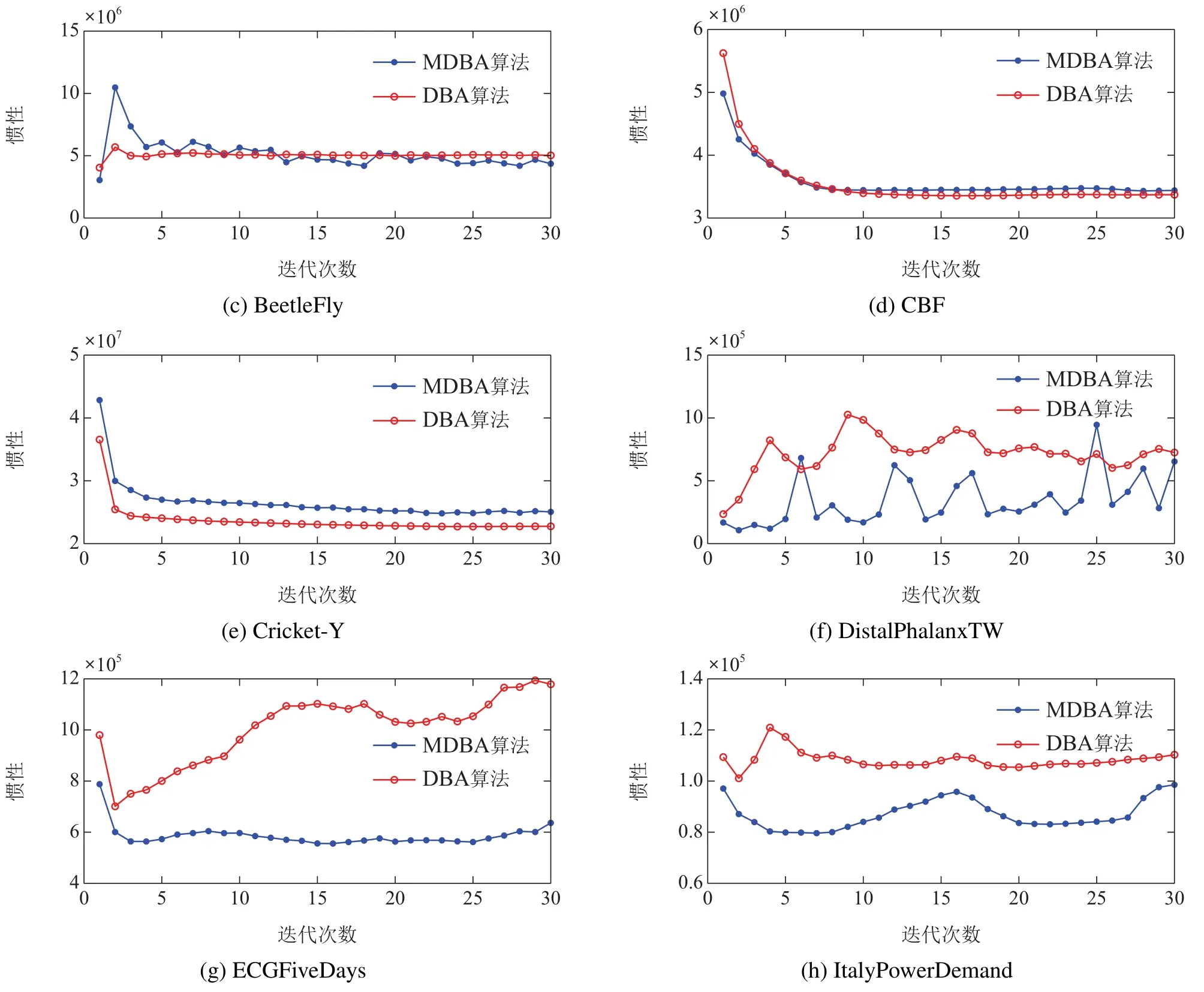
图7 各数据集MDBA算法惯性变化对比Fig.7 Comparison of inertia changes of MDBA algorithm in each data set
为了验证MDBA算法的惯性收敛性,对数据集各个类别的数据均进行收敛性分析,本次实验合并数据集测试集和训练集中相同类别,对不同类别的数据使用MDBA算法进行迭代,迭代次数为100次,各数据集中各类别的簇中心惯性变化见图8.
由图8分析可知,总体上MDBA算法对于数据集中不同类别的数据惯性变化较为平稳,变化幅度较小.对于少数数据集中的类别,簇中心惯性随着迭代次数的增加呈水平直线变化.MDBA算法簇中心惯性的收敛性明显强于ISS,但相比于UWM,收敛性有所下降.例如DistalPhalanxTW与ECGFiveDays数据集簇中心惯性波动幅度所有增加.
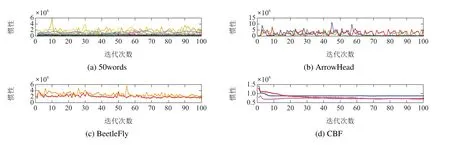

图8 各数据集不同类别的簇中心惯性变化Fig.8 Inertia changes of cluster centers in different categories of data sets
综上所述,MDBA算法中和了单个改进机制的惯性收敛效果和惯性值质量.减弱了簇中心更新异权机制对于数据集的挑选的严格性,弥补了簇中心更新异权机制惯性值质量差的缺陷,继承了确定性选择策略下惯性值的优越性,增强了确定性选择策略的惯性收敛性,达到二者融合的效果,从惯性值和收敛性综合角度评判MDBA算法前瞻性.
5 结论
针对DBA算法初始簇中心选择的随机性问题,本文提出了簇中心初始选择策略,针对DBA算法簇中心更新时序列无差性问题,提出了簇中心更新异权机制.簇中心初始选择策略的最终的簇中心惯性接近原算法中初始簇中心随机选取的惯性均值;簇中心更新异权机制能够加强迭代过程中的惯性收敛性,在迭代次数较少的情况下获得较优的簇中心;MDBA算法能够提高簇中心惯性质量的同时加强惯性收敛性.
虽然MDBA算法在聚类问题中复杂度优于原算法,但受到求解序列DTW的复杂度影响,总体上算法复杂度过高.后续如果能够将DTW算法进行改进,可以提高MDBA算法的求解效率.

