非线性时变系统的自耦PID控制方法
苏 杰,曾喆昭
(长沙理工大学电气与信息工程学院,湖南长沙 410076)
1 引言
由于机理复杂、所处环境未知,大部分工业系统往往存在时变不确定性和非线性,因此近几十年来,非线性时变系统的控制问题得到了国内外学者的广泛关注,并获得了行之有效的研究成果[1-5].现有控制方法主要包括:神经网络控制方法[6-9]、迭代学习与重复学习控制方法[10-12]、backstepping控制方法[13-15]、非线性自学习PID控制方法[16-17]等.尽管现有这些控制方法都获得了行之有效的控制效果,然而也都存在各自的局限性,如:神经网络控制方法存在结构复杂、计算量大、实时性欠佳的局限性;迭代学习与重复学习控制方法不仅对初始状态要求过高,而且需要多次重复迭代才能实现有效控制,因而存在计算量过大、实时性差的局限性,而且只能实现周期轨迹的跟踪控制;backstepping方法存在“微分爆炸”的局限性,尽管通过干扰观测器或跟踪微分器可以解决“微分爆炸”问题,然而却增加了控制系统的复杂性;而自学习非线性PID控制方法则存在增益鲁棒性欠佳与抗扰鲁棒性差的局限性.为了解决现有控制方法存在各种局限性问题,文献[18-20]提出了一种自耦PID控制方法,并根据与被控对象模型无关的速度因子形成了增益整定规则(量纲换算规则),不仅有效解决了PID的整定难题,而且解决了PID增益鲁棒性差与抗扰动鲁棒性差的科学问题.然而,文献[18-20]的自耦PID控制方法只提出了速度因子的概念,没有对速度因子做系统深入研究,而且根据积分步长来镇定速度因子,不便于实际应用.为此,在现有基础上,本文对速度因子进行了全面系统的分析,并科学证明了速度因子与系统稳态误差之间的关系,为期望跟踪精度的决定提供了理论依据.同时为了避免动态过程中因积分饱和引起的超调与振荡现象,本文还设计了一种基于误差的自适应速度因子,有效提高了动态品质和稳态性能,解决了基于时间的自适应速度因子不适合期望输出频繁突变的情况.理论分析与仿真结果都表明了自耦PID (auto-coupling proportional-integral-differential,ACPID)控制方法在不确定非线性时变系统控制中的有效性.
2 问题背景
考虑某二阶时变不确定非线性系统[12]
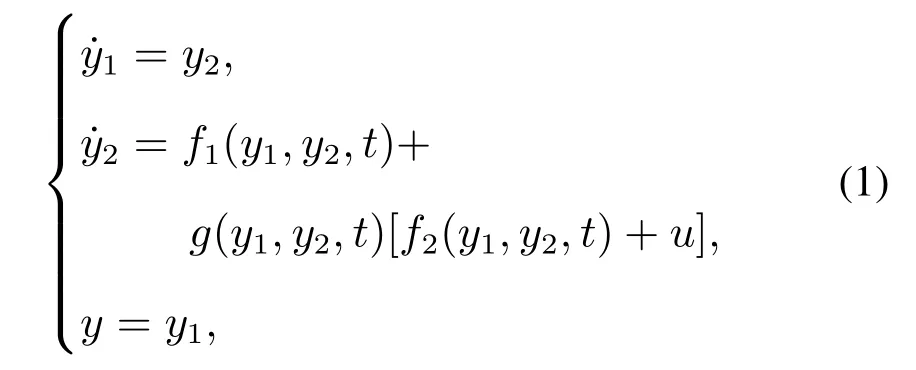
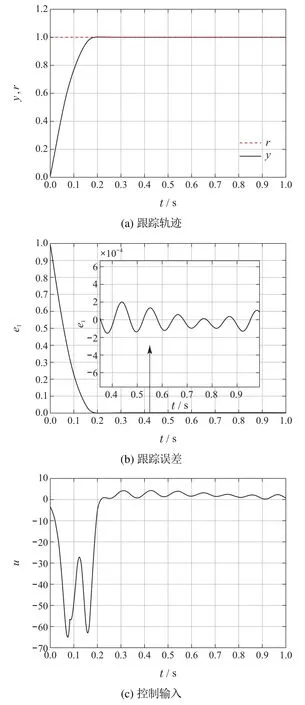
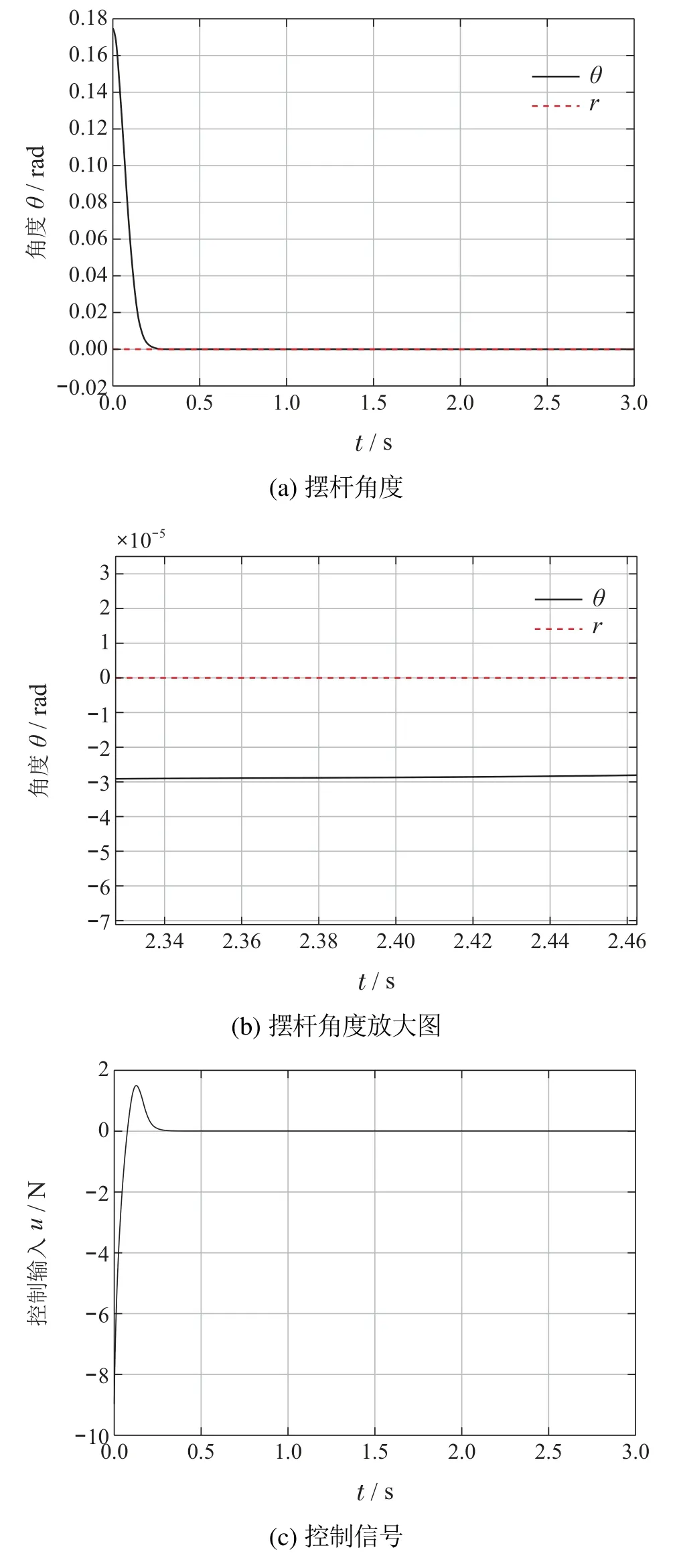
其中:y1,y2∈R是可测量的两个状态,u ∈R是控制输入,y ∈R是系统输出.f1(·),f2(·)∈R是未知非线性函数,g(·)是系统未知控制增益,且0 根据韩京清研究员对总和扰动(或扩张状态)的定义思想[21],本文将非线性时变系统的未知动态定义为总和扰动y3,即 其中b0是未知控制增益的估计值(不要求精确),且0 因而非线性时变系统(1)可等价映射为一个未知线性系统 由于系统(3)是系统(1)的等价映射,因此根据系统(3)形成的控制器可以对系统(1)施加有效控制.假设被控对象的期望输出为r,针对系统(3)的控制问题,定义跟踪的误差及其积分与微分分别为 显然,误差系统(4)实际上是一个在总和扰动y3反向激励下的受控误差系统.设跟踪误差初值为,跟踪误差微分的初值为.为了使该误差系统从任意不为0的初始状态快速趋向稳定的平衡原点(0,0),要求合理设计控制律(控制力)u.本文将使用ACPID控制理论方法来设计控制律(控制力)u. ACPID的主要特点在于通过速度因子zc将比例(P)、积分(I)和微分(D)3个不同属性物理环节自行耦合在一起,进而形成一个功能各异、目标一致的协同控制信号,即ACPID控制律模型如下[19]: 由于ACPID控制律(5)可分解为比例控制力up=、积分控制力和微分控制力ud=3zce2/b0等3项,其理论依据之一是每一项都由速度因子进行量纲换算,使得3个不同属性的控制力遵循量纲匹配规则;其二是通过速度因子建立了3个不同属性环节之间的内在关系,使得比例控制力、积分控制力和微分控制力在控制过程中能够表现出功能各异且目标一致的协调控制行为,纠正了传统PID3个不同控制力各自为战的不协调控制行为.这两个理论依据正是曾喆昭教授提出的控制理论思想[19-20]. 由ACPID控制律(5)组成的闭环控制系统如图1所示. 图1 ACPID控制模型Fig.1 The control model of ACPID 定理1当|y3|≤ε1<∞,||≤ε2<∞,且0 证将式(5)建立的ACPID控制律代入式(4),可得闭环系统 可知式(9)为ACPID闭环系统的零状态响应,由此可定义闭环系统传输函数为 当zc>0时,由于系统函数H(s)有且仅有唯一的三重极点s=-zc<0在S域左半平面,由复频域分析理论可知,闭环系统(7)或(9)是稳定的.又因为zc与被控对象的模型无关,因而系统(7)或(9)是大范围鲁棒稳定的. 根据系统(10),闭环系统(9)可简化为 根据系统传输函数(10)可得其单位冲击响应为 因此闭环系统(11)的时域解为 其中“*”表示卷积积分运算. 显得不够严谨,为此,本文做了上述纠正. 为验证本文ACPID控制系统部分限幅的合理性,现给出积分饱和受限时的稳定性定理. 定理2当0 证当ACPID控制系统积分环节饱和受限时,可设uim=aui,其中0 将积分饱和时的ACPID控制律(16)代入式(4),可得 设A(s)=,则 多 项 式A(s)是霍尔威兹多项式的充要条件是A(s)的罗斯阵列的第1列元素全部正定.而A(s)的罗斯阵列第1列共有4个元素,分别为 当0 综上所述,当ACPID的积分控制力在uim=aui,且0 由上述定理可知,当|y3|<∞,且|¨r|<∞时,只要zc>0,由ACPID控制器组成的闭环系统是大范围鲁棒稳定的,而且具有良好的抗总和扰动鲁棒性,表明ACPID的速度因子具有很大的整定裕度.在控制过程中,为避免比例控制力up=特别是积分控制力ui=过大而引起超调与振荡现象,要求使用较小的速度因子.然而,若zc太小,系统的动态响应速度、抗扰动能力以及稳态控制精度都会降低.因此,为了兼顾系统动态品质和稳态性能,应使用自适应速度因子. 由于被控对象的动态快慢特性可由时间尺度τ来反映,τ越大,被控对象动态变化速度(1/τ)就越慢,否则反之,因此,只需ACPID的速度因子大于被控对象动态变化速度(1/τ),即可实现有效控制,即zc>1/τ,因此,可设定ACPID最小速度因子为 其中1<α≤10. 对于不确定非线性时变系统而言,时间尺度τ难以获取,为此,本文利用被控对象由动态过程进入稳态过程的过渡过程时间T0(调节时间)来大概估计时间尺度τ,可设T0=10τ,结合式(19)可得 其中:1<α≤10,T0是过渡过程时间. 本文根据式(22)设计了基于误差的自适应速度因子模型 其中:1<α≤10,β=1+α. 由于文献[19]设计的是基于时间的自适应速度因子,不适合期望输出频繁突变的情况,为此,本文设计了式(23)所示基于误差的自适应速度因子. 为验证本文方法的有效性,并便于比较分析,设被控对象及其初始状态与文献[12]完全相同,即 下列仿真实验中都使用完全相同的控制器和自适应速度因子,且设控制输入允许的最大幅值为um=80. 例1时变参数、初始状态和期望轨迹与文献[12]完全相同,即: 系统初始状态:y1(0)=1,y2(0)=3π;期望轨迹:r(t)=1+sin(2πt)+0.25 sin(4πt).本文控制结果如图2所示,文献[12]的结果如图3所示. 图2 ACPID控制结果Fig.2 The control results of ACPID 由图2可知,本文使用ACPID控制方法获得的结果不仅响应速度快而且稳态跟踪控制精度高(最大绝对误差为5×10−3).然而,文献[12]使用重复学习控制方法不仅涉及多达7个参数,计算复杂,而且图3是经过40个周期的重复学习后,第40个周期的控制结果,因而实时性差、跟踪控制精度不高(最大绝对误差为2.2×10−2).此外,文献[12]只适合于周期轨迹的跟踪控制,而且要求系统初始状态与期望轨迹的起点或终点重合,因而存在较大的局限性. 图3 文献[12]控制结果Fig.3 The control results in[12] 例2保持时变参数不变,设期望轨迹为阶跃轨迹(非周期轨迹),且初始状态远离期望轨迹的情况下(y1(0)=0,y2(0)=3π),本文控制方法的结果如图4所示. 由图4可知,对于非周期的阶跃轨迹,本文ACPID控制方法依然能有效控制,不仅具有较快的响应速度(0.2 s达到稳态),而且无超调、无振荡,稳态最大绝对误差仅为2×10−4,而文献[12]对该轨迹则是无法进行控制的.由此可知,本文控制ACPID方法不仅响应速度快,控制精度高,具有较强的抗扰鲁棒性,而且对于同一系统的不同跟踪轨迹具有普遍适用性. 图4 ACPID阶跃跟踪结果Fig.4 The step tracking results of ACPID 为进一步证明本文控制方法的有效性,以小车倒立摆系统为例进行控制研究.小车倒立摆由小车、摆杆、轨道和驱动电机组成,结构如图5所示. 图5 小车倒立摆示意图Fig.5 Structure of cart-pole inverted pendulum 设小车质量为M,摆杆质量为m,x为小车至轨道中心的位移,u为控制输入,转动惯量为I,小车摩擦系数为b,倒立摆摆杆角度为θ.因此小车倒立摆系统可表示为 其中:M=1.2 kg,m=0.072 kg,l=0.36 m,b=0.08,I=0.0018 kg·m2. 对于式(26)所示的小车倒立摆系统,只考虑控制摆杆的角度,不控制小车的位移.设期望的摆杆角度为0 rad,则摆杆的误差误差及其微分可表示为e1=-θ,e2=-,根据本文自耦PID控制理论思想,在不考虑积分环节的情况下,建立自耦PD控制律为u=设T0=1 s,α=5,β=6,则有:zc=50e−6|e1|.给定系统初始状态为x(0)=0.1 m,θ(0)=,仿真结果如图6所示.由图6可知,在本文方法控制下,小车倒立摆系统的摆杆角度能在0.3 s内达到稳态,不仅无超调和振荡现象,而且稳态绝对误差仅为3×10−5rad,表明了本文控制方法的有效性. 图6 小车倒立摆系统控制效果Fig.6 Control effect of car inverted pendulum system 在ACPID控制理论的基础上,本文建立了最小速度因子模型及其基于绝对误差的自适应速度因子模型,其目的是有效避免因积分饱和引起超调与振荡现象的问题.本文控制方法不仅控制器结构简单、计算量小、便于实际应用,而且是一种完全不依赖于对象模型的控制理论方法.仿真结果不仅表明了良好的动态品质与稳态性能,而且有效解决了文献[12]无法跟踪非周期轨迹的局限性,在非线性不确定未知系统控制领域具有广泛的应用前景.

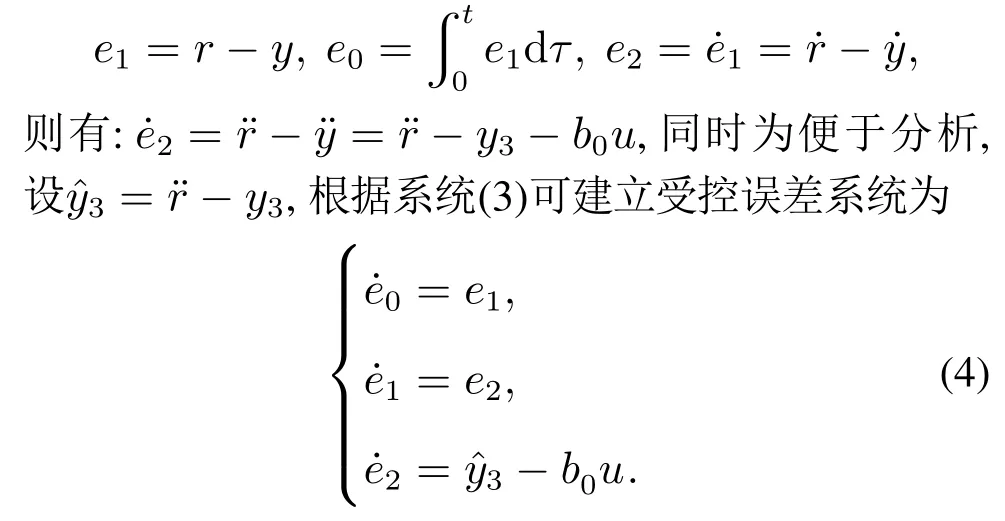
3 自耦PID控制原理
3.1 自耦PID控制律模型


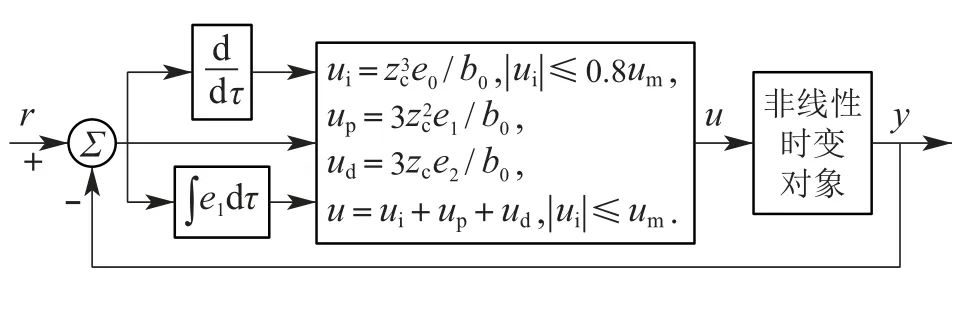
3.2 ACPID闭环系统分析


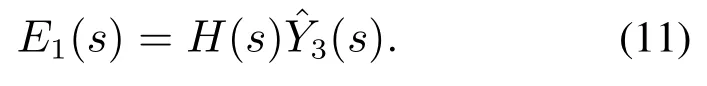
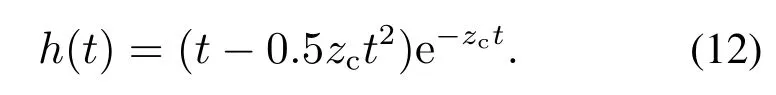

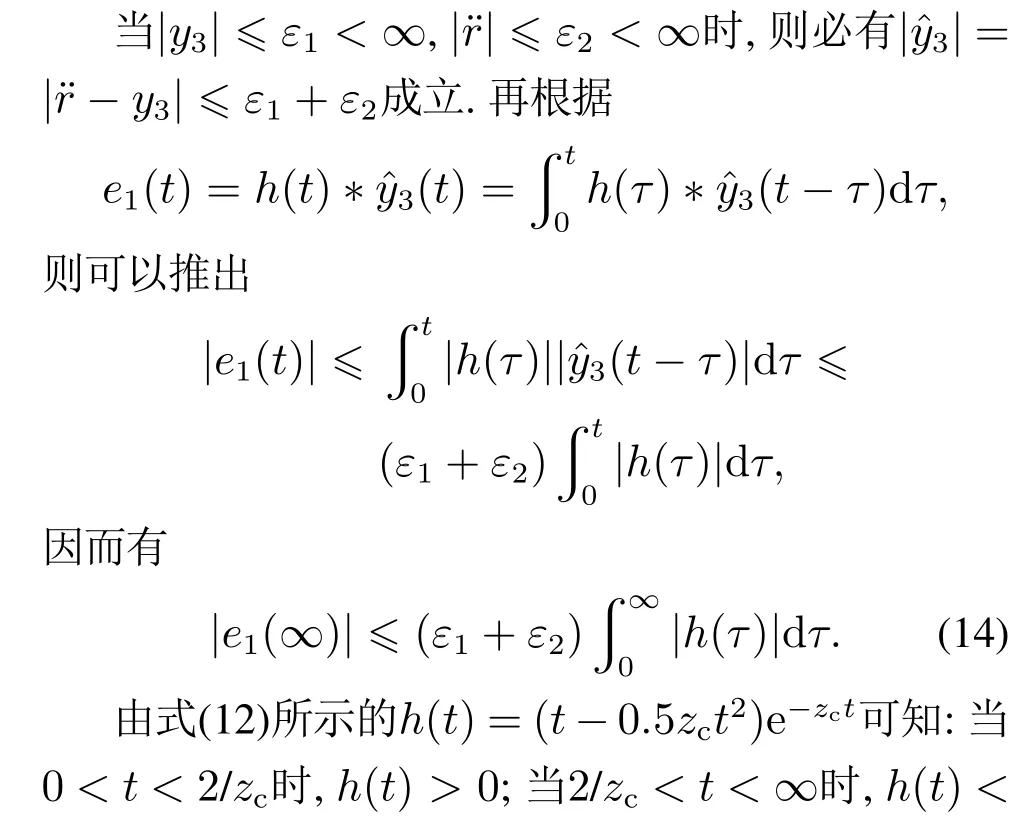




3.3 自适应速度因子模型



4 仿真研究
4.1 二阶非线性时变系统的仿真研究




4.2 小车倒立摆实际系统的仿真研究


5 结论

