电能表检验台体串联机械臂时间最优轨迹规划

欧 新，周 璐，张 鸷，吴月家，赵云斌

贵州电网有限责任公司 贵阳供电局，贵阳 550002

随着机器人技术的发展和工业自动化的推进，串联机械臂被应用于越来越多的场景中，时间最优[1-4]轨迹规划能够有效缩短机械臂运动时间，提高工作效率，具有十分重要的研究意义。目前主流的时间最优轨迹规划方法主要分为两个阶段，首先利用轨迹插值算法对机械臂运动路径进行拟合；其次通过优化算法对机械臂在拟合路径上的运动时间进行优化。

较为常用的机械臂轨迹插值算法有样条插值和多项式插值两种，其中三次样条插值、B样条插值等样条插值算法通过部分已知路径点拟合完整路径，适用于要求复杂的连续运动任务[5-6]；三次多项式插值、五次多项式插值等多项式插值算法由机械臂首末状态决定运动路径，适用于点到点运动[7]。在实际应用场景中点到点运动或简单的连续运动更为常见，并且简单的连续运动可以离散为几个点到点运动，所以机械臂点到点运动轨迹规划的研究更具广泛适应性[8]。为了保证关节首末角位移、角速度及角加速度均可控，文中选择五次多项式插值算法对机械臂的运动路径进行拟合。

机械臂运行时间一般通过群体智能优化算法进行优化，如遗传算法、蚁群算法、粒子群算法等[9-12]，其中以遗传算法在机械臂时间最优轨迹规划问题中的研究最为深入，许多学者针对机械臂运动特性提出了很多针对性的改进。文献[13]针对超冗余度机械臂提出了一种时间最优轨迹规划方法，并用标准多种群遗传算法优化了机械臂的运行时间。文献[14]提出一种自适应精英遗传算法，在五次多项式插值轨迹规划算法的基础上，采用基于遗传算法框架的精英群和自适应调节机制提高优化性能。文献[15]中通过自适应调整交叉和变异的概率，达到更快的收敛速度。文献[16]提出一种基于混沌局部搜索的双种群遗传最优时间轨迹规划算法，利用双种群遗传算法全局搜索能力强、进化速度快和混沌算法局部搜索能力强的优点，规划时间最优的运动轨迹。文献[17]在三次样条插值轨迹规划算法的基础上采用聚类方法改进遗传算法，保留优良个体的同时兼顾种群多样性，提高搜索效率。

上述文献中分别通过多种群、自适应交叉和变异、贪婪选择策略等方面对遗传算法进行改进，然而仍然存在算法收敛一致性差，收敛速度有待提高等问题。为此文中提出一种基于改进多种群遗传算法的轨迹规划方法，在五次多项式插值算法拟合的机械臂运动路径上，通过改进的多种群遗传算法对机械臂运动时间进行优化，改进之处包括：设计含有惩罚项的适应度函数，降低不满足运动学约束条件的个体被选择的概率；引入贪婪选择策略，按照比例保留父代种群优秀个体，替换子代种群较差个体；自适应调整交叉和变异概率，加快算法收敛速度。以ER-4iA机械臂为实验对象，通过仿真实验验证所提算法的可行性，并将所提算法与蚁群算法、粒子群算法、标准遗传算法和标准多种群遗传算法进行对比实验，结果表明所提轨迹规划方法具有更好的收敛一致性和更快的收敛速度。

1 串联机械臂运动学模型

文中提出的机械臂时间最优轨迹规划方法适用于串联机械臂结构，串联机械臂由一组刚性连杆通过转动关节串联而成，是目前最常见的机械臂结构。1955年Denavit和Hartenberg提出的D-H方法是建立串联机械臂运动学模型的标准方法[18]，其原理是在各连杆的末端关节处建立坐标系，相邻坐标系通过4个参数计算变换矩阵，从而建立机械臂末端和基坐标之间的位姿变换关系。然而标准D-H方法无法表示连杆关于y轴的运动，且在树形机械臂结构的建模上存在歧义，这些问题在1986年Khalil和Kleinfinger提出的改进D-H方法中得以改善[19]。改进D-H方法在连杆首端关节处建立坐标系，且相邻坐标系之间的参数变换顺序和标准D-H方法完全相反，是目前最常用的串联机械臂运动学建模方法。

以图1所示的六自由度串联机械臂为例，通过改进D-H方法建立机械臂各连杆坐标系的步骤如下：

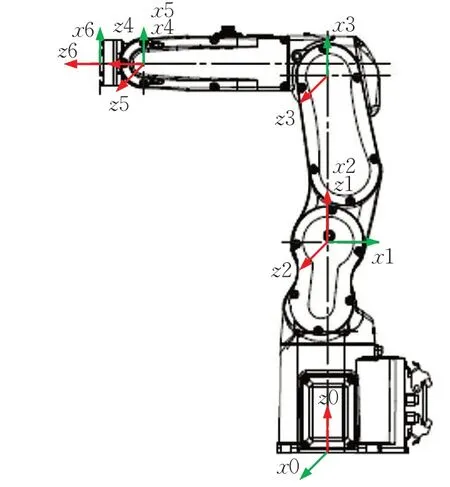
图1 六自由度串联机械臂结构Fig.1 Structure of tandem manipulator with six degrees of freedom

（1）确定Z轴：Zi轴沿关节轴i的方向。

（2）确定原点：原点Oi为Zi轴和Zi+1轴的交点或其公垂线与Zi轴的交点。

（3）确定X轴：Xi轴沿Zi轴和Zi+1轴的公垂线由关节轴i指向关节轴i+1，若Zi轴与Zi+1轴相交则Xi轴垂直于它们所在的平面。

（4）确定Y轴：Yi轴由右手定则确定。

以地面坐标系为基坐标系，相邻两个关节坐标系之间的变换矩阵可以通过链式法则计算：

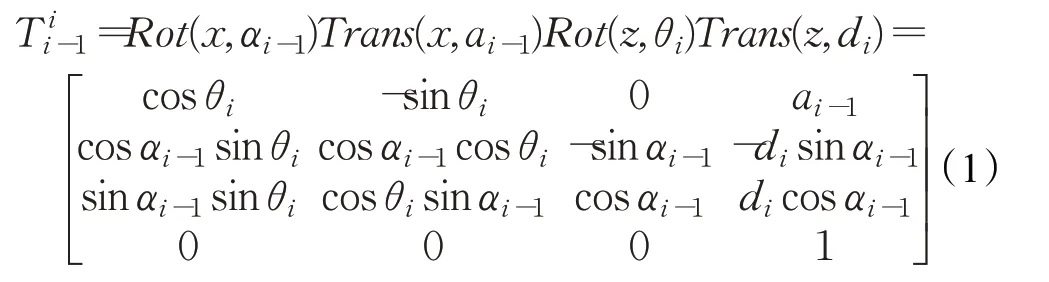
其中，αi-1是Zi-1到Zi绕Xi-1正方向转动的角度，ai-1是转动后的Zi-1到Zi沿Xi-1正方向的距离，θi是移动后的Xi-1到Xi绕Zi正方向转动的角度，也是实际控制机械臂运动的关节角度，di是转动后的Xi-1到Xi沿Zi方向上的距离，坐标系(Xi-1,Yi-1,Zi-1)通过上述四个变换之后能够与坐标系(Xi,Yi,Zi)完全重合。机械臂末端坐标系与基坐标系的变换矩阵为：

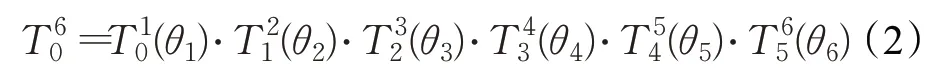
根据上述机械臂运动学模型，已知各关节角度即可计算机械臂末端位姿，通过控制机械臂各关节角θ关于时间的角位移曲线Qi(t)就能够控制机械臂末端的运动轨迹，从而将机械臂的空间轨迹规划问题转换为各关节角运动曲线规划问题。

2 优化问题描述

串联机械臂在工业生产和物流运输等领域拥有广泛的应用，时间最优轨迹规划能够有效缩短机械臂的运行周期，提高工作效率。文中以机械臂点到点轨迹的运行时间为主要优化目标，假设机械臂从初始关节状态Q0运动到终止关节状态Qf的时间为tf，则目标函数可以表示为：

此外机械臂在运动过程中应严格满足其固有的运动学约束条件，因此优化问题可以描述为：

式中，V、A、J分别表示机械臂各关节运动过程中的角速度、角加速度和角加加速度，Vs、As、Js分别为它们的额定最大值。

对于五次多项式插值算法拟合的运动轨迹，关节角θ关于时间的角位移曲线Q(t)、角速度曲线V(t)、角加速度曲线A(t)及角加加速度曲线J(t)可以表示为：

通过求解五次多项式中的6个系数a0～a5即可得到各关节运动曲线表达式。

3 机械臂时间最优轨迹规划方法

3.1 多种群遗传算法

多种群遗传算法是遗传算法的一种改进，多个种群同时沿不同方向进化，种群之间通过移民算子进行交互，最优解从各种群最优个体构成的精英种群中产生，算法流程图如图2所示。

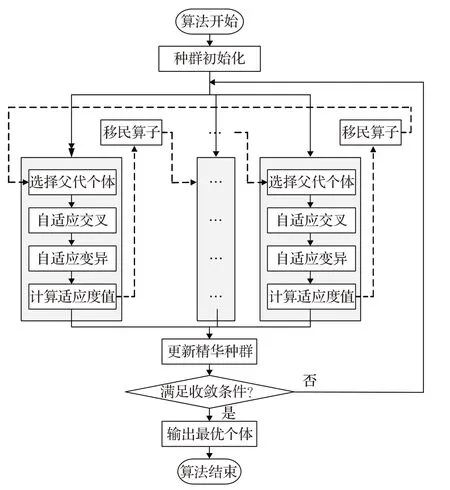
图2 多种群遗传算法流程图Fig.2 Flow chart of multi-population genetic algorithm

其中将自身种群的最优个体作为移民算子，在每次选择父代个体之前迁移到相邻种群中，替代目标种群中的最劣个体，这有三点好处：

（1）为目标种群带去新的优秀的基因，丰富了目标种群的多样性。

（2）目标种群陷入局部最优时，移民算子的加入有利于打破僵局。

（3）种群之间协同进化，加速种群收敛。

3.2 基于改进多种群遗传算法的时间最优轨迹规划

针对机械臂点到点轨迹规划任务，以五次多项式轨迹插值的时间tf为优化目标，在多种群遗传算法的基础上进行相应的调整和改进，提出一种基于改进多种群遗传算法的时间最优轨迹优化方法，具体改进点如下：

带有惩罚项的适应度函数。根据式（4）描述的优化问题，设计如下个体适应度函数：

式中，x是个体基因的表现形式，即运行时间tf,kt是时间调和系数，Ei是各关节根据机械臂运动约束条件设计的惩罚项，其计算公式为：

贪婪选择策略：在父代种群选择阶段，按照一定比例保留当前种群的部分优秀个体，经过交叉和变异操作之后通过重插入的方法，用保留个体逐个替换子代种群中的较差个体，既保证了优秀个体不被破坏，也能加快算法收敛。

自适应交叉和变异：在多种群遗传算法中，为了实现不同种群进化方向的差异性，各种群的交叉和变异概率Pm和Pc在特定范围[PmL,PmU]和[PcL,PcU]内随机产生，为了达到更快的收敛速度，将交叉和变异概率设置为随迭代次数自适应降低，迭代早期通过较大的交叉和变异概率保证种群多样性，迭代后期通过较小的交叉和变异概率保留最优解并加快收敛速度，自适应交叉和变异概率表达式为：

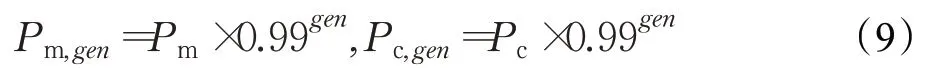
其中，gen为当前算法迭代次数。

3.3 算法整体流程

综上所述，文中设计的基于改进多种群遗传算法的机械臂时间最优轨迹规划方法主要步骤如下：

（1）设置主要参数：基因编码长度chromlen，种群大小popsize，种群数量popnum，式（7）～（9）中的参数。

（2）初始化种群。

（3）进行贪婪选择、自适应交叉和变异操作。

（4）计算适应度值：对个体解码获取实数x，根据式（5）和式（6）计算五次多项式系数，得到各关节角速度、角加速度、角加加速度函数，根据式（7）和式（8）计算个体适应度函数值。

（5）获取移民算子和精英种群。

（6）判断是否满足收敛条件：若满足则输出最优个体，不满足则进行移民操作并重复步骤（3），收敛条件为精英种群最优个体保持一定的代数。

4 仿真实验与结果分析

4.1 仿真实验平台

文中使用发那科的ER-4iA机械臂作为实验验证平台，通过MATLAB中的Robotics Toolbox工具箱进行机械臂仿真建模。根据改进D-H方法计算ER-4iA机械臂的D-H参数如表1所示，用SerialLink函数建立如图3所示的ER-4iA机械臂仿真模型。

图3 ER-4iA机械臂仿真模型Fig.3 Simulation model of manipulator ER-4iA

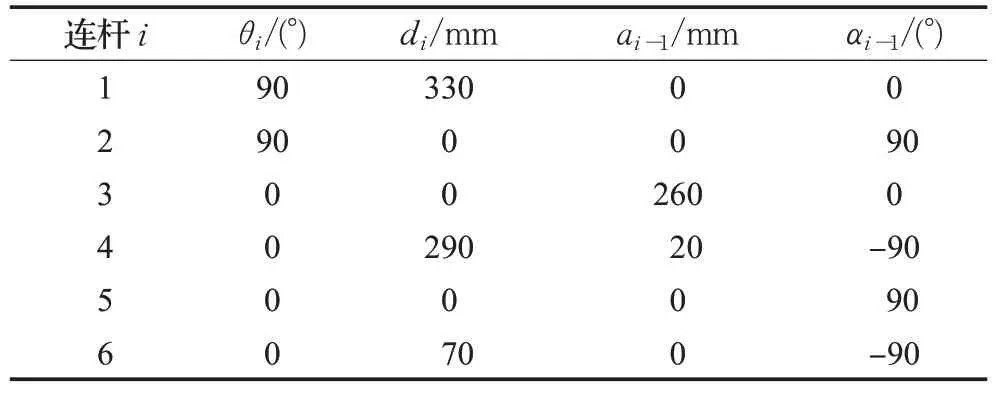
表1 ER-4iA机械臂D-H参数Table 1 D-H parameters of manipulator ER-4iA

为了在实验平台上验证文中时间最优轨迹规划方法的可靠性，基于控制变量的原则，设置机械臂各关节始末角度、速度和加速度为定值：

对此只要提供机械臂运行时间tf就可以求解五次多项式的6个系数a0～a5，从而根据式（5）得到各关节角速度函数、角加速度函数和角加加速度函数。

4.2 算法仿真实验

设置基因编码长度chromlen=10,种群大小popsize=40,种群数量popnum=10,适应度函数中的时间调和系数kt=0.1，惩罚系数kV=kA=kJ=1，随机交叉概率范围[PmL,PmU]=[0.7,0.9]，随机变异概率[PcL,PcU]=[0.001,0.05]，机械臂关节运动学约束条件如表2所示。

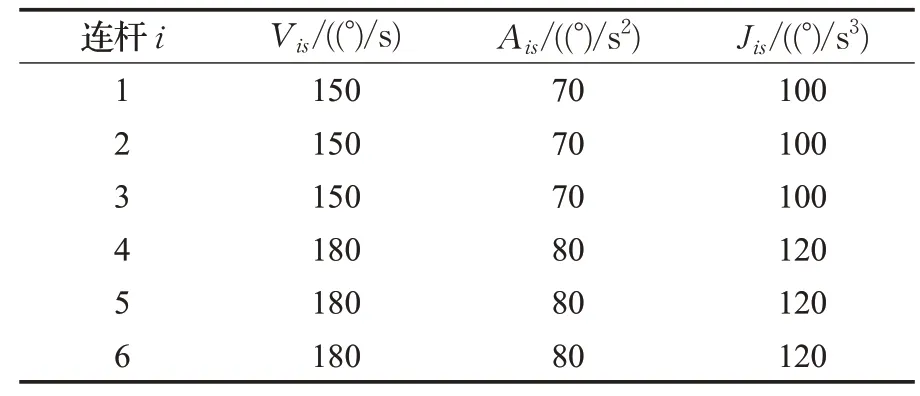
表2 机械臂关节约束条件Table 2 Constraints of mechanical arm joint

按照上述参数设置进行多组实验，最优运行时间均为3.914 9 s，此时各关节角位移、角速度、角加速度及角加加速度随时间的变化曲线如图4所示。

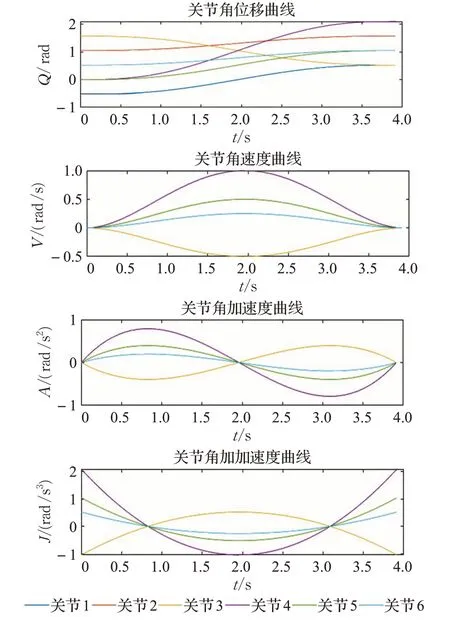
图4 各关节角运动曲线Fig.4 Angular motion curves of each joint

仿真实验结果表明：各关节角运动轨迹平滑，始末点状态均符合参数设定，运动过程中角速度、角加速度及角加加速度均无突变，并始终满足机械臂关节约束条件，验证了文中设计的机械臂时间最优轨迹规划方法的有效性。

4.3 优化算法对比实验

为了验证文中改进的多种群遗传算法具有更好的收敛一致性和更快的收敛速度，在优化目标函数和收敛条件不变的情况下，分别用蚁群算法（ACO）、粒子群算法（PSO）、标准遗传算法（SGA）、标准多种群遗传算法（MPGA）和文中改进的多种群遗传算法（IMPGA）对4.1节中的运动轨迹进行10组重复实验，对比5种优化算法在收敛一致性和收敛速度上的表现，实验结果如表3所示。

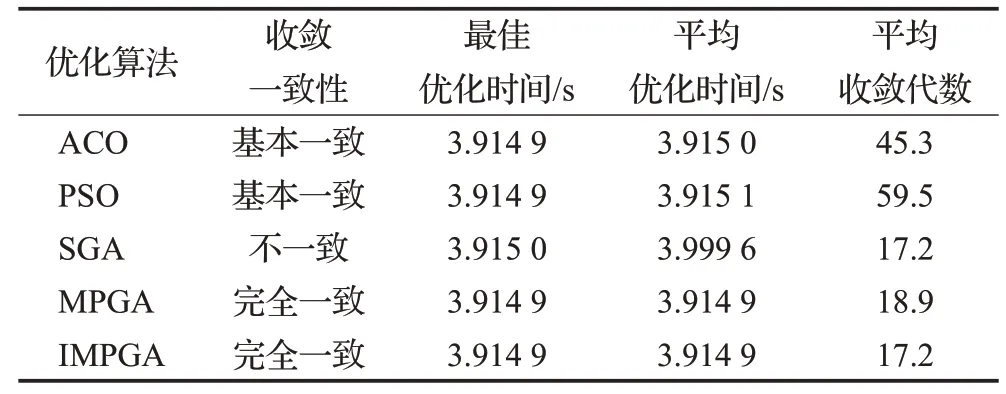
表3 5种优化算法的实验结果Table 3 Experimental results of five optimization algorithms

5种优化算法的进化过程如图5所示，对比实验结果表明：蚁群算法和粒子群算法收敛速度较慢，多次重复实验收敛结果基本一致；标准遗传算法收敛速度较快但多次重复实验结果很难保持一致，算法稳定性较差；标准多种群算法收敛速度较快且在多次重复实验中均能搜索到全局最优解；文中改进的多种群遗传算法在标准多种群算法稳定搜索最优解的基础上，进一步加快了收敛速度。由此验证了文中改进的多种群遗传算法相较于其他同类算法具有更好的收敛一致性和更快的收敛速度。

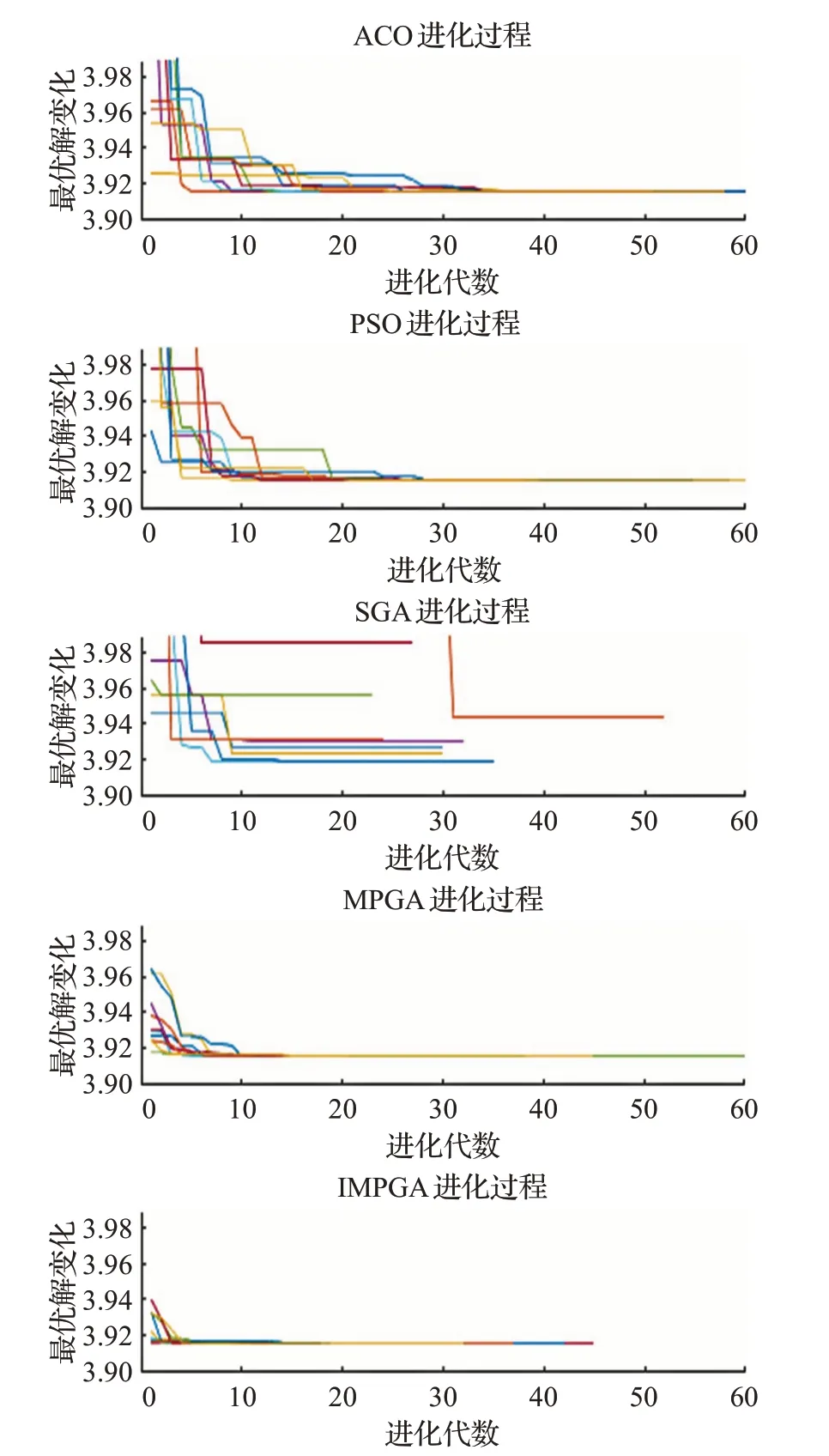
图5 5种优化算法的进化过程Fig.5 Evolution of five optimization algorithms

5 结束语

针对串联机械臂时间最优轨迹规划问题，在5次多项式轨迹插值的基础上，利用改进的多种群遗传算法对机械臂运动轨迹进行优化。以发那科ER-4iA机械臂为实验验证平台，以机械臂点到点轨迹运行时间为优化目标，分别用蚁群算法、粒子群算法、标准遗传算法、标准多种群遗传算法和文中提出的改进多种群遗传算法进行优化。实验结果表明文中算法在多组重复实验中均能收敛至全局最优解，且相较于同类算法具有更快的收敛速度；以最优运行时间拟合机械臂运动轨迹，各关节角速度、角加速度及角加加速度曲线均平滑且满足机械臂运动学约束条件，验证了文中改进多种群遗传算法的机械臂时间最优轨迹规划方法的可行性。

文中以机械臂点到点运动的时间作为优化目标进行仿真和对比实验，然而机械臂实际工作任务可能由多段点到点运动构成，文中改进的多种群遗传算法在以多段运动时间为目标的多目标优化任务中是否仍然具备优势仍有待验证。此外，在某些特殊任务中，除了对机械臂关节运动有所约束，往往还对末梢速度、关节力矩等指标有所要求，如何调整算法适应更为复杂的优化目标也是未来潜在的研究方向之一。